优化初三数学复习教学方案例析讨论

余丽云

摘 要：初三复习阶段时间紧，任务重，如果教师不能抓住学生的认知规律进行有针对性的教学方法设计，就无法达到“温故知新”的教学效果。站在一线教学的角度，撇开三轮复习的流程叙述，从提升初三数学复习效率的教学实践和方法上展开讨论与分析。

关键词：初三数学；复习教学；基础知识；分层引导；实践探索

初三阶段面临中考，是紧张的复习阶段。而传统的题海战术复习方式忽略了学生的认知规律，不能抓住学生的认知需求，更不能引导学生生成知识脉络。因此，我们一定要从学生的认知学情出发，设置有针对性的阶段性复习方案，指导学生巩固和梳理以前学过的知识，迁移内化使之形成知识网络，提升解决实际问题的能力。鉴于此，笔者结合多年的初三教学经验，撇开三轮复习的流程分析，从复习教学方法的角度来进行例析与讨论。

一、掌握考试重点，完善基础认知

1.掌握考试方向

所谓“知己知彼方能百战不殆”。要想初三复习更有效率，更有针对性，一线教师就务必先认真阅读相关科目的《考试说明》。除了把握中考形式及动态、中考试题类型、难度、方向等热点问题以外，我们还得注意是否增加了新考点，只有这样我们才能明确中考的侧重点，在引导学生复习时才能做到心中有数，然后我们再针对考点，系统地引导学生回顾基本概念到运用实践，这样才能提高学生应对能力，提高备考效率。

2.梳理基础知识

每年的中考可能微调考试的侧重点，可能创新题型。但是万变不离其宗，都是对学习过的基本知识和概念的运用能力实际考查。所以，复习过程中我们首先要做的就是根据《考试说明》和《教学大纲》的要求，带领学生再一次系统地认知基本的知识概念细节。只有事无巨细全面把握数学概念的每一个细节，我们才能在各种考查中应对自如、游刃有余。

具体教学中，我们还是要以教材为主线，实际上我们完全可以在教材的例题和练习中找到往年中考例题的原型，所以我们要在学生复习了基本概念后，趁热打铁布置有针对性的典型试题，让学生通过练习和体验，从而建立知识模型，掌握整个类型题目的解决方案，便于在将来的考查中对号入座，解决实际问题。

二、初步实践体验，树立运用意识

学以致用是教学的最终目的，但是从理论知识到运用能力需要通过逐步的实践体验来完善。这就要求我们在引导学生夯实基本概念后，要趁热打铁及时设置有针对性的试题来让他们运用新复习的知识点完成初步运用尝试。教学过程中，我们通常从最切近概念的简单试题入手。唯有如此，方能让学生认知知识的灵动性，认识到理论知识如何运用于实际问题。

比如，复习了“相似三角形性质”基本概念后，我们就必须及时设置试题来让学生实践相似三角形性质在解决实际问题中的运用：

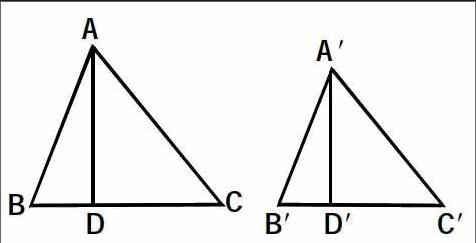
例题：如右图，△ABC∽△A′B′C′，其中AD和A′D′分别是BC与B′C′边上的高，已知AC：A′C′=3：2，A′D′=4，那么AD是多少。

学生根据相似三角形性质，由△ABC∽△A′B′C′可以推出△ADC∽△A′D′C′，于是就有AC：A′C′=AD：A′D′=3：2，算得AD=6。

这个小例题是掌握相似三角形性质及比例关系后最典型、最模型化的。设置这个例题不是让学生复习比例求得结果的，而是让学生树立运用意识，掌握能运用相似三角形的比例关系求得未知数技能的。

三、根据学情反馈，巧设分层引导

由于学生的学习能力、认知层次和知识结构等方面客观上存在差异，所以我们也不能设置一刀切的复习模式。我们应该以生为本，复习过程的回答问题等方面来捕捉有效反馈信息，这样我们才能全面了解学生的真正实力，才能摸清他们的实际认知规律，然后有针对性地整合教学内容分层引导，这样才能让每个层次的学生都能学有所获。

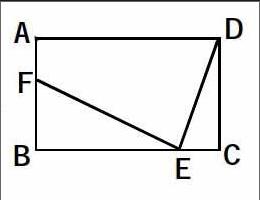
我们在复习过程中解决模式试题中的综合题型时，不能一刀切地进行流水账的讲解，这样肯定会让基础薄弱的学生无法跟进。如果放慢速度，又可能消磨优等生的复习意志。所以，我们就要根据学生对例题的不同反馈进行有针对性的分层指导，争取让不同层次的人都有收获。如例：如右图，在矩形ABCD中，AB=m（m是大于0的常数），BC=8，E为线段BC上的动点（不与B，C重合），连结DE，作EF⊥DE与射线BA交于点F，设CE=x，BF=y，（1）求y关于x的函数关系式，（2）假如m=8，那么x怎样取值，y的值最大，最大值是多少？（3）如果y=，那么m怎样取值△DEF为等腰三角形？

这样的综合性题目是中考的必考题，例题中的三个问题就代表三个层次，我们可以通过分析学生的回答情况，总结分析大家的知识掌握情况。笔者经过反馈分析，发现大概有下面几种情况：①大约20%的学生不知所措，找不到下笔的思路；②大概一半的学生能做完第二问；③还有30%的学生能成功解答第三问。有了这样的问题反馈，我们就可以设定相应的复习教学方案：层次①的学生不能运用数与形结合的思想，缺乏观察图形之间的关系的能力。针对这样的学生，我们可以设置一些简单的几何证明题，让他们通过观察和联系掌握画辅助线，帮助他们健全几何思维，联系数形结合思想，来完成形象知识转化的能力。具体到这道题我们就要启发他们思考怎样才能将x与y建立联系，很显然，只要做辅助线DF，就一目了然了：BE2+BF2=EF2；DC2+EC2=DE2；DE2+EF2=DF2；而AD2+AF2=DF2，所以就有了BE2+BF2+DC2+EC2=AD2+AF2，所以就有（m-y）2+82=x2+m2+（8-x）2+y2得出函数为：。层次②的学生能解决到第二步说明已经掌握了基本的数形结合思想和二次函数最值问题，他们许多错就错在将y=带入到了第一步的思维方式中，让问题复杂化。其实，我们可以启发他们用代数思想直接带入问题二的结果就可以简化问题得出正确解题思路。

复习过程中，我们面对的是认知能力参差不齐的学生，复习过程中我们也不能讳疾忌医，也要能通过信息反馈认清他们的不同认知层次，然后进行有针对性的引导和启发，这样才能做到具体问题具体分析，有针对性地引导各个认知层次的学生完成知识迁移。

四、设置开放问题，体验知识运用

这几年的中考试题比较侧重考查学生综合运用知识，手机信息，这就要求我们在复习过程中一定要能引导学生能通过搜集和分析相关数据和信息，建立理论知识到实践运用的联系。因此，在复习过程中，我们一定要摒弃题海战术，代之以丰富多彩的、活泼、灵动的方式和方法来引导学生体验知识生成，如此才能让学生从实际体验中变抽象为形象，掌握数学知识的精髓。

比如，我们复习了“相似三角形”的基本应用后，我们就将学生带到操场上，可以设置开放性的练习：哪位学生能利用所学知识测出阳光下的旗杆高度？学生根据提示和启发，纷纷设置方案，整合能测绘到的相关数据，最终得出一个优化方案：如右图，假设AB是旗杆，BC是旗杆的影子，那么我们可以找一根棍子DE，让DE立在BC上并使其影子顶点与旗杆影子顶点重合，这样一来就和上例解决方法一样了：DE：AB=CD：BC，这个比例关系中，我们很容易测出棍子长度DE，旗杆和棍子的影长BC与DE，这样我们就很容易得出问题答案。这样，学生就通过完成任务，完整地体验到知识到运用的全过程，潜移默化中埋下数学运用与实践思维的种子。

五、客观对待错误，弥补知识漏洞

学习本质上就是不断发现不足并及时弥补漏洞的过程。其实，初三复习就是为了查漏补缺，最大限度地帮助学生弥补知识漏洞。所以，我们在遇到错误时，一定要引导学生去积极探索错误的根源，如此方能变废为宝，完善知识运用。

例如：设x的一元二次方程（k-1）x2-2x-1=0有两个不相等实数根，请问K的取值。

许多学生一看是有二次幂就按二次方程来解：二次方程有两个不相等的实数根的话Δ>0，也就是22+4k>0，解得k的取值范围是k>0.

这样对吗？有人举出了反例：这个范围内k-1的话方程就是一次方程只有一个实数根了。有反例就说明错了，这里我们来引导学生认知错误，进行反思：

（1）犯错的根源？（惯性思维，忽略了二次幂系数是0的情况。）

（2）如何正确求解？（本题：由于方程存在两个不等的实数根，所以Δ>0得出：k>-1然后再考虑满足一元二次方程成立的条件 最终得出k的取值范围是k>-1且k≠1。）

利用错误资源反思是学习和迁移知识的必经阶段，所以，复习过程中我们一定要鼓励学生敢于承认错误，养成纠错反思的习惯，做到在学习中反思，在反思中进步。

上文是笔者结合多年的一线初三教学经验对几种经典复习教学法的分析与讨论，总而言之，复习过程是知识再现的过程，我们一定要根据学生的实际认知规律有针对性地整合复习内容，引导学生逐步完成基础概念认知，然后再结合实践训练帮大家开拓思路，建立模型。只有这样才能让学生在复习过程中夯实基础，迁移知识，生成运用能力。

参考文献：

[1]吴灵姿.提高初中数学复习课有效性的策略[J].数学学习与研究，2013（04）.

[2]惠民.复习教学在初三数学教学中的应用[J].教育教学研究，2014（09）.

[3]宋丽明.谈谈初中数学复习课的有效策略[J].城市建设理论研究，2012（33）.

编辑 薄跃华