基于粗糙集-支持向量机的软件缺陷预测*

2015-03-27马小平

计算机工程与科学 2015年1期

关键词：软件缺陷约简粗糙集

孟倩，马小平

(1.中国矿业大学信电学院，江苏徐州 221008；2.江苏师范大学计算科学与技术学院,江苏徐州 221116)

基于粗糙集-支持向量机的软件缺陷预测*

孟倩1,2，马小平1

(1.中国矿业大学信电学院，江苏徐州 221008；2.江苏师范大学计算科学与技术学院,江苏徐州 221116)

软件缺陷预测已成为软件工程的重要研究课题，构造了一个基于粗糙集和支持向量机的软件缺陷预测模型。该模型通过粗糙集对原样本集进行属性约减，去掉冗余的和与缺陷预测无关的属性，利用粒子群对支持向量机的参数做选择。实验数据来源于NASA公共数据集，通过属性约减，特征属性由21个约减为5个。实验表明，属性约减后，Bayes分类器、CART树、神经网络和本文提出的粗糙集—支持向量机模型的预测性能均有所提高，本文提出的粗糙集支持向量机的预测性能好于其他三个模型。

粗糙集；支持向量机；软件缺陷；预测；粒子群

1 引言

软件已经成为影响国民经济、军事、社会生活的重要因素。高可靠性和复杂的软件系统非常依赖于所采用软件的可靠性。根据ISO 9000的定义，软件缺陷(Defect)是指“未满足与预期或者规定用途有关的要求”，是导致软件系统出错、失效、崩溃甚至机毁人亡的潜在根源[1]。软件缺陷预测技术是根据历史数据以及已经发现的缺陷等软件度量数据，预测哪些模块有出错倾向，对软件开发者合理配置资源，从而降低研发成本、缩短产品开发周期和提高软件质量起到重要作用。

软件缺陷预测本质上是一个模式识别的过程，它的核心是分类，目前用于软件缺陷预测的方法有Bayes分类器[2]、分类回归树[3]、聚类分析[4]和神经网络[5]等。由于软件缺陷受到多种复杂度度量属性的综合作用，至今尚没有一种软件缺陷预测的通用的分类模型。近年来，用支持向量机SVM(Support Vector Machine)来实现基于分类问题的预测已经成为研究热点。SVM是一种通用的前馈神经网络，其核心是经验风险最小化原则，有效地解决了小样本、高维数、非线性等学习问题，它由Vapnik V N在1992年首次提出[6]，可以用于模式分类和非线性回归。近年来，各国学者开始用SVM进行软件可靠性方面的预测。国际上，Gray D等人[7]利用支持向量机对软件缺陷进行预测取得了不错的效果；Mishra B等人[8]提出用于软件可靠性预测的模糊支持向量机。国内崔正斌等人[9]提出了遗传优化支持向量机软件可靠性模型；张艳等人[10]将支持向量机回归模型用于测控软件故障预测。

作为一种新的学习机器，SVM也存在一些有待完善的地方，SVM的性能与其参数的选择密切相关，而其参数选取没有理论上的指导。本文应用粒子群PSO(Particle Swarm Optimization)来进行支持向量分类机参数选择。SVM方法另一不足之处是，由于SVM在训练中需要进行大量的矩阵运算，当处理的数据量过大时，SVM的训练时间过长、速度变慢[11]。波兰科学院院士Pawlak Z教授于1982 年提出的粗糙集理论RS(Rough Sets)是继概率论、模糊集、证据理论之后的又一个刻画不完整性和不确定性的数学工具，它不需要任何先验知识，可分析出信息间相互关系，可以在保持分类能力不变的条件下进行属性约简,达到数据信息精炼化的目的[12]。

为了提高软件缺陷预测能力，本文融合RS方法和SVM方法，建立一种基于粗糙集-支持向量机(RS-SVM)的软件缺陷预测模型，在不改变样本分类质量的条件下，运用粗糙集属性约简方法作为预处理器对样本进行降维处理。通过属性约简，本文发现可以仅使用软件度量的少量特征属性(McCabe环路复杂度、McCabe设计复杂度、操作符种类、操作数种类和总代码行数)来进行软件缺陷预测，这样不但可以减少样本的维数，缩短SVM样本训练时间，还可以降低数据采集难度，并提高分类器性能。属性约简后利用PSO算法对SVM进行参数优化，并用SVM方法建立软件缺陷预测模型。

2 原理与算法

2.1 粗糙集

属性约简是粗糙集理论的核心内容之一，属性约简就是在保持知识库分类能力不变的条件下，删除其中不相关或不重要的属性。

2.2 支持向量机

SVM的基本思想是非线性映射将输入向量映射到一个高维特征空间，在高维特征空间寻求最优划分超平面，使得尽可能多地将2 类数据点正确分开，同时使分类间隔最大[6]。

对于给定样本点：(xi,yi)，i=1,…,n，xi∈Rd，yi∈{+1,-1}。xi为输入特征，yi为决策属性。构造决策函数最终可以转化为一个典型的二次规划问题,即在约束条件:

(1)

之下,求下列函数最小值:

(2)

其中，w为分类面权系数向量；b为分类域值；C是惩罚系数,C>0；ξ是训练样本关于分离面的偏差。引入Lagrange乘子αi，得到其对偶形式：

(3)

其中，0≤αi≤C,i=1,…,l。

将输入向量映射到一个高维特征空间,引入满足Mercer条件的K(xi,x)核函数,最终得到决策函数为：

(4)

这就是支持向量机，式(4)中具有非0值的ai对应的向量支撑了最优分类面，因此成为支持向量。目前常用的核函数有线性核函数、多项式核函数、径向基核函数和Sigmoid核函数。

2.3 粒子群算法

粒子群优化算法[13]中，优化问题的每个解对应搜索空间的一个粒子，记为:

pi=(pi1,pi2,…,pin),i=1,2,…,m

(5)

其中,m为粒子的个数，n为粒子的维数。每个粒子有一个速度vi=(vi1,vi2,…,vin)，决定它的方向和位置。粒子群优化算法首先初始化粒子群，计算出每个粒子的适应值，然后通过迭代搜索最优解。在每次迭代中，对于每个粒子，粒子通过追踪两个极值来更新自己：一个是粒子自己找到的最优解，称为个体极值；另一个是整个粒子群目前找到的最优解，称为全局极值。当找到个体极值和全局极值后,粒子按式(6) 和式(7) 来更新自己的速度和位置：

(6)

(7)

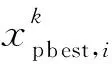
3 RS-SVM软件缺陷预测建模

本文建立一种基于RS-SVM的软件缺陷预测模型，如图1所示。整个分类过程分成三个阶段：首先, 采用粗糙集理论对样本进行预处理，以去掉冗余属性，并剔除无效数据。软件缺陷特征属性之间存在着一定的相关性，经过属性约简不仅可消除指标间的信息重叠，还起到降维的作用，提高了模型运行速度，也大大降低了缺陷数据采样的工作量。然后，利用粒子群对支持向量机的参数进行优化，寻出最优参数。最后，利用最优参数建立SVM训练模型，对经过预处理的样本集进行分类训练和预测。

Figure 1 Prediction model based on RS-SVM

4 RS-SVM的软件缺陷预测实验

4.1 实验环境及实验数据来源

根据前述思想，本文利用台湾ChangChih-chung等人[14]开发的LIBSVM工具箱，在MatlabR2009b下编写了粗糙集和粒子群PSO算法程序。

美国国家航空航天局NASA(NationalAeronautics&SpaceAdministration)较早就启动了软件缺陷预测技术的研究，并基于航空系统软件开展了软件模块的度量数据库项目MDP(MetricDataProgram)，为缺陷预测研究提供数据支撑,MDP原数据集可从网址http://mdp.ivv.nasa.gov下载。本实验数据来源于MDP的JM1数据集,JM1数据集从一个用C++语言编写的地面预测系统项目中得到，共有10 878个模块，每个模块的22个属性中有21个特征属性和1个目标属性，21个特征属性中5个属性来源于代码度量，3个来源于McCabe度量，12个来源于或派生于Halstead度量，1个属性是模块分支数。

4.2 不平衡数据和脏数据处理

软件缺陷数据集是类不平衡的，在JM1数据集中，有缺陷的模块有2 102个，无缺陷的模块有8 776个。WeissG等人[15]研究了训练数据集的类分布与分类器的分类性能之间的关系。结果显示,相对平衡的类分布通常会得到较理想的结果。

NASA软件度量数据集已经被广泛应用于研究，数据集本身可能存在的问题近期引起了一些学者的注意，ShepperdM[16]指出,NASA的数据集中存在着大量的“重复数据”和“矛盾数据”这种脏数据，已经严重影响了软件缺陷预测的结果。

基于以上原因，本文对JM1数据集进行了删除脏数据的处理，并最终随机提取1 200个数据作为实验样本，有缺陷样本和无缺陷样本各占50%。

4.3 粗糙集属性约简

在MatlabR2009b下实现粗糙集属性信息熵约简算法，得出属性决策表的两个约简：R1={1,4,6,8,9,11,21}和R2={5,6,19,20,21}，其中的数字为原数据集中属性序号。这样，条件属性由21个分别约简为7个和5个，下文分别称为属性约简1和属性约简2，将分别做实验测试其性能。

4.4 评价指标

本文实验用准确度(Accuracy)、精确度(Precision)、查全率(Recall)和F-度量(F-Measure)来评价和比较预测模型，这些度量都来源于混淆矩阵，如表1所示。

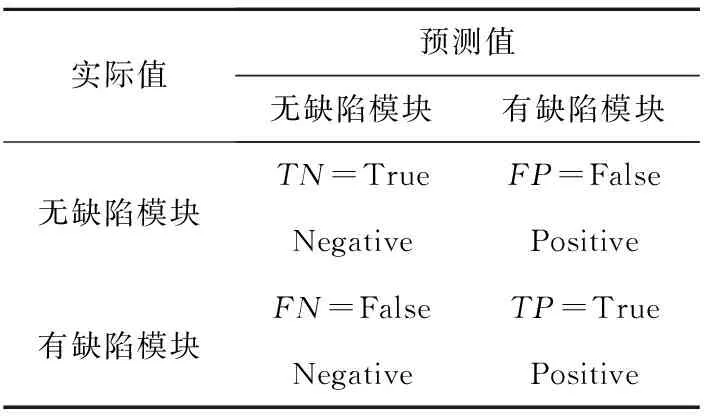
Table 1 Confusion matrix

Accuracy：预测结果和实际结果一致的模块在整个测试集合中的比例。

Accuracy=(TP+TN)/(TP+FN+FP+TN)

(8)

Precision：预测为有缺陷模块中实际为有缺陷模块比例。

Precision=TP/(TP+FP)

(9)

Recall：有缺陷模块被正确识别的比例。

Recall=TP/(TP+FN)

(10)

F-Measure：是Precision和Recall的调和平均数。

F-Measure=2/((1/precision)+(1/Recall))

(11)

4.5 基于PSO的SVM参数的选择

基于2.3节介绍的粒子群优化算法及其在Matlab R2009b下的实现，进行SVM最优参数选择，本文采用径向基核函数，需要优化的参数有惩罚系数C和核参数γ。

以1-Accuracy的值作为粒子群的适应值的评价函数， 1-Accuracy的值越小越好。

设置粒子群参数：群体规模为20，粒子向量维数为3，加速因子C1=2，C2=2，最大迭代次数为300。对未经过属性约简的SVM模型，粗糙集属性约简1为特征属性的RS-SVM1和约简2为特征属性的RS-SVM2模型分别经过PSO优化，最优参数见表2 。

Table 2 Optimization of PSO parameters

4.6 实验结果及分析

将特征值归一化到[-1，1]，消除了因量纲不同可能引发的影响。本文采用10折交叉验证的方法，样本集被随机等分成10个子集，任取其中一个子集作为测试样本集，其余9个子集作为训练样本集，实验总做10次，以10次实验的性能指标平均值来评价一个算法的性能。将未经过属性约简的SVM模型、RBF神经网络、CART树、Bayes分类器分别经过10折交叉验证，实验结果比较如表3所示。

Table 3 Experimental results of models with all attribute

把由粗糙集约简R1为特征属性的RBF神经网络、CART树、Bayes分类器分别称为RS-RBF1、RS-CART1和RS-Bayes1，这三个模型连同RS-SVM1模型，分别经过10折交叉验证，实验结果比较如表4所示。

Table 4 Experimental results of models with attribute reduction 1

把由粗糙集约简R2为特征属性的RBF神经网络、CART树、Bayes分类器分别称为RS-RBF2、RS-CART2和RS-Bayes2，这三个模型连同RS-SVM2分别经过10折交叉验证，实验结果比较如表5所示。

Table 5 Experiment results of models with attribute reduction 2

从表3～表5可以看出，不论粗糙集属性约简前还是约简后，Bayes分类器预测效果都比较差，Bayes分类器假设特征向量的所有分量之间是独立的，在缺陷预测中，特征属性之间不是绝对独立的，所以使用此模型得到的分类结果会比较差。基于CART树和RBF神经网络方法的预测性能都明显好于Bayes方法，但当CART树分类回归树划分得太细时,会对噪声数据产生过度拟合的问题。RBF神经网络结构选择无统一理论指导，预测效果都比SVM略差一点。SVM具有严格的理论和数学基础，基于结构风险最小化原则，保证学习机器具有良好的泛化能力，需要设定的参数相对较少，引入PSO进行参数优化，提高了参数选择的效率和模型预测性能。

粗糙集属性约简后，四种模型预测性能都有所提高，总的来看，属性简减2的预测性能更好。原样本数据含有大量冗余特征属性，21个特征属性中某些属性是由其他属性通过数学运算计算出来的，如大部分Halstead度量属性，有些属性对缺陷预测是无关紧要的，如一些代码度量属性。

性能比较好的属性约简2中的属性有5个，分别是McCabe环路复杂度(CYCLOMATIC_COMPLEXITY)、McCabe设计复杂度(DESIGN_COMPLEXITY)、操作符种类(NUM_UNIQUE_OPERANDS)、操作数种类(NUM_UNIQUE_OPERATORS)和总代码行数(LOC_TOTAL)。根据软件工程的知识可知，这5个属性相互之间基本不相关，并且是影响软件可靠性的重要属性。实验也表明，对原属性集中21个特征属性通过粗糙集约简掉冗余特征后只保留5个特征属性，四种模型缺陷预测性能不但没有降低反而都有所提高。

5 结束语

本文将粗糙集属性约简方法引入到软件缺陷预测中。原软件度量特征属性中含有大量冗余属性，通过粗糙集属性约简，仅保留了少量特征属性，不但提高了软件缺陷预测性能，而且大大减少采样工作量，提高了工作效率。本文利用PSO算法对SVM进行参数选择并用SVM算法对处理过的样本集进行软件缺陷预测，通过实验与其他软件预测方法比较，表明本文提出的方法具有更好的预测效果。下一步工作将研究如何进一步提高软件缺陷预测的准确度。

[1] Wang Qing,Wu Shu-jian,Li Ming-shu.Software defect prediction[J].Journal of Software,2008,19(7):1565-1580.(in Chinese)

[2] Muson J C,Khoshgoftaar T M. The detection of fault-prone programs[J]. IEEE Transactions on Software Engineering,1992,18(5):423-433.

[3] Briand L C, Basili V, Hetmanski C J. Developing interpretable models with optimized set reduction for identifying high-risk software components[J].IEEE Transactions on Software Engineering,1993,19(11):1028-1044.

[4] Zhong S,Khoshgoftaar T M,Seliya N.Analyzing software measurement data with clustering techniques[J]. IEEE Intelligent Systems,2004,19(2):20-27.

[5] Qiao Hui,Zhou Yan-zhou,Shao Nan,et al. Research of software reliability prediction model on AGA-LVQ[J]. Computer Science,2013,40(1):179-182. (in Chinese)

[6] Vapnik V N. The nature of statistical learning theory[M]. New York:Springer-Verlag, 1995.

[7] Gray D, Bowes D, Davey N, Neill D,et al. Using the support vector machine as a classification method for software defect prediction with static code metrics∥[C]Proc of the 11th International Conference on Engineering Applications of Neural Networks,2009:223-234.

[8] Mishra Bharavi,Shukla K K. Support vector machine based fuzzy classification model for software fault prediction[C]∥Proc of the 5th Indian International Conference on Artificial Intelligence(IICAI 2011),2011:693-708.

[9] Cu Zheng-bin,Tang Guang-ming,Yue Feng. Software reliability prediction model based on support vector machine optimized by genetic algorithm[J].Computer Engineering and Applications,2009,45(36):71-74. (in Chinese)

[10] Zhang Yan,Ren Zi-hui.SVM-based forecasting methods for software fault[J].Journal of Chinese Computer Systems,2010,31(7):1380-1384. (in Chinese)

[11] Sanchez V D. Advanced support vector machines and kernel method[J]. Neurocomputing,2003, 55(1-2):5-20.

[12] Pawlak Z. Rough Sets:Theoretical aspects of reasoning about data(theory and decision library D)[M].Boston:Kluwer Academic Publishers,1992.

[13] Eberhart R,Kennedy J.A new optimizer using particle swarm theory[C]∥Proc of the 6th International Symposium on Micro Machine and Human Science, 1995:39-43.

[14] Chang Chih-chung,Lin Chih-jen.LIBSVM:A library for support vector machines[EB/OL].[2009-10-09].http://www.csie.ntu.edu.tw/～cjlin/libsvm.

[15] Weiss G, Provost F. Learning when training data are costly: The effect of class distribution on tree induction[J]. Journal of Artificial Intelligence Research,2003,19(1):315-354.

[16] Shepperd M,Song Qin-bao,Sun Zhong-bin,et al.Data quality: Some comments on the NASA software defect data sets[J]. IEEE Transactions on Software Engineering,2013,39(9):1208-1215.

附中文参考文献：

[1] 王青,伍书剑,李明树.软件缺陷预测技术[J].软件学报, 2008,19(7):1565-1580.

[5] 乔辉，周雁舟，邵楠，等. 基于AGA-LVQ神经网络的软件可靠性预测模型研究[J]. 计算机科学，2013,40(1):179-182.

[9] 崔正斌,汤光明,乐峰.遗传优化支持向量机的软件可靠性预测模型[J].计算机工程与应用,2009,45(36)：71-74.

[10] 张艳，任子晖.一类基于支持向量机的软件故障预测方法[J].小型微型计算机系统，2010,31(7):1380-1384.

MENG Qian,born in 1970,PhD candidate,associate professor,her research interests include database technology, and software engineering.

马小平(1961-),男,四川绵阳人，博士，教授，研究方向为控制理论及应用。E-mail:xpma@cumt.edu.cn

MA Xiao-ping,born in 1961,PhD,professor,his research interest includes control theory and applications.

高性能计算专栏约稿

一、刊物简介

《计算机工程与科学》是由国防科技大学计算机学院主办的中国计算机学会会刊，是国内外公开发行的计算机类综合性学术刊物。本刊已先后被列为中文核心期刊、中国科技信息研究所中国科技论文统计分析源期刊(中国科技核心期刊)、中国科学引文数据库来源期刊(CSCD核心期刊)、中国学术期刊(光盘版)全文入编期刊、中国期刊网全文入编期刊、中国学术期刊综合评价数据库来源期刊。

二、征稿范围(但不限于)

目前，国内高性能计算的研究方兴未艾，为更好地宣传目前国内高性能计算领域的研究和应用现状，我刊常年设有高能性能计算专栏，重点是面向国内高性能计算领域的研究和应用。包括：

(1)系统研制技术：体系结构、系统软件、软件并行化、多核编程、编译技术、GPU计算、低功耗技术、系统优化技术。

(2)系统应用：EDA设计仿真、CAE、数值计算、计算化学、计算物理、材料设计、量子力学、分子动力学、流体力学、工业设计、图像渲染、生物信息、生命科学、气象、天文、金融、石油勘探、工程计算、地震资料处理、集群管理、并行应用软件开发(MPI、OpenMP、CUDA)、Linpack测试研究、超算服务等。

三、投稿要求

(1)投稿方式：采用“计算机工程与科学在线投稿系统”(http://www.joces.org.cn)投稿。投稿时请在备注栏中注明“高能性能计算专栏”字样。

(2)稿件格式：参照《计算机工程与科学》下载中心的排版规范(网站上提供了论文模版，可下载)。

(3)投稿文章未在正式出版物上发表过，也不在其他刊物或会议的审稿过程中，不存在一稿多投现象；保证投稿文章的合法性(无抄袭、剽窃、侵权等不良行为)。

(4)其他事项请参阅投稿须知： http://www.joces.org.cn/CN/column/column291.shtml

(5)专刊投稿文章按《计算机工程与科学》正常标准收取审稿费和版面费，但将会优先发表；发表之后，将按《计算机工程与科学》的标准支付稿酬，并赠送样刊。

《计算机工程与科学》编辑部

Software defect prediction usingrough sets and support vector machine

MENG Qian1,2,MA Xiao-ping1

(1.School of Information and Electrical Engineering,China University of Mining and Technology,Xuzhou 221008;2. College of Computer Science and Technology,Jiangsu Normal University,Xuzhou 221116,China)

The prediction of software defects has been an important research topic in the field of software engineering. The paper focuses on the problem of defect prediction. A classification model for predicting software defects based on the integration of rough sets and support vector machine model (RS-SVM) is constructed. Rough sets work as a preprocessor in order to remove redundant information and reduce data dimensionality before the sample data are processed by support vector machine. As a solution to the difficulty of choosing parameters, the particle swarm optimization algorithm is used to choose the parameters of support vector machines. The experimental data are from the open source NASA datasets. The dimensions of the original data sets are reduced from 21 to 5 by rough sets. Experimental results indicate that the prediction performances of Bayes classifier, CART tree, RBF neural network and RS-SVM are all improved after the dimension of the original data sets are reduced from 21 to 5 by rough sets. Compared with the above three models, RS-SVM has a higher prediction performance.

rough sets;support vector machine;software defect;prediction;particle swarm optimization

1007-130X(2015)01-0093-06

2014-08-12;

2014-10-19基金项目：国家自然科学基金资助项目(61303183)；江苏省自然科学基金资助项目(BK20130204);高等学校博士学科点专项科研基金资助项目(20120095120023)

TP311.5

10.3969/j.issn.1007-130X.2015.01.014