不同水力梯度对渗透系数影响研究

王福刚, 张佳慧, 于吉洋， 许 静

(1. 吉林大学 环境与资源学院, 吉林 长春 130021; 2. 辽宁省化工地质勘查院, 辽宁 锦州 121007)

实验技术与方法

不同水力梯度对渗透系数影响研究

王福刚1, 张佳慧1, 于吉洋2， 许 静1

(1. 吉林大学 环境与资源学院, 吉林 长春 130021; 2. 辽宁省化工地质勘查院, 辽宁 锦州 121007)

通过室内实验的方法,针对水力梯度对渗透系数的影响展开研究。实验筛分出粗砂、中砂、细砂分别进行不同水力梯度的渗流实验,并对每组实验数据进行分析、整理,通过计算机作图等手段研究水力梯度与渗透系数二者之间的关系。得到渗透系数随水力梯度变化的规律。

渗透系数; 水力梯度; 渗透速度

渗透系数也称水力传导系数,是指饱和多孔介质单位水力梯度时的渗流速度。渗透系数不仅取决于岩石的性质(如粒度成分、颗粒排列、充填状况、裂隙性质及其发育程度等),而且与渗透液体的物理性质(容重、黏滞性等)有关[1]。渗透系数可以通过数值模拟反演以及室内实验等方法求得[2]。实验室测定渗透系数可以通过达西定律等方法进行计算。达西定律也称线性渗透定律,是研究渗流和介质渗透性与水力梯度之间的数量关系的重要定律[3]。一般说来,根据达西定律,渗透系数与水力梯度之间无相关关系,但从一些实验研究中发现,水力梯度在一定的条件下对渗透系数是有影响的。对渗透系数的研究一直为专家和学者所重视。邱珍锋等[4]提出渗透特性与物质成分、颗粒级配、颗粒形状、密实度等因素相关，并通过室内垂直渗透试验,探讨了土体颗粒形状、颗粒级配和试样密实度对粗粒土渗透系数的影响。张家发等[5]通过实验证明颗粒形状对渗透特性的影响规律：颗粒越圆,其渗透系数越大;颗粒越不规则,其渗透系数越小。长期以来,已经证明土体的渗透性与土体密实度、类型、颗粒形状、物质、颗粒级配、成分以及温度、压力等许多因素相关[6-10]。以往对于介质特性以及实验流体等对渗透系数的影响研究较多,而水力梯度对渗透系数的影响却无人问津。因此本次研究内容从水力梯度对渗透系数的影响出发,结合水力学中的相关公式和理论成果,选择不同粒径的石英砂为介质,在3种不同特征的介质中通过调整水力梯度进行室内实验,研究不同水力梯度对渗透系数的影响。本文的研究结果将对地下水资源评价、地下水渗流分析、溶质运移模拟等研究与计算提供参考,具有实际应用价值[11]。

1 实验设计

1.1 实验装置

实验的装置见图1,装置是由5 mm厚的有机玻璃制成,高140 cm,内径15 cm的砂柱(柱体由3部分组成:上下各有8 cm的水流缓冲区;中部为渗流区,长90 cm,其侧面等距分布有7个测压孔)。在进水口采用水泵进行供水,以确保稳定的水头供水。通过控制进水口水头高度,保证实验在定水头下进行[12]。

图1 实验装置

实验时将砂柱与测量系统之间的管路连接好,将砂柱放倒并调整水平。初始水头差为12 cm,打开水泵,向砂柱内注水,记录下各测量值的初始值。平衡状态持续足够长时间后单位时间间隔流量不变时,测量该水头差的流量(每组实验测得5个数据)。然后通过控制进水水头装置改变水头差(22、32、42、52、62、72 cm),依照上述方法进行实验,并记录实验数据。

1.2 实验材料选择

由于石英砂质地坚硬、耐磨,化学性质稳定,故主要选用石英砂作为实验介质。实验所需的砂样为3种不同粒径的石英砂,选取孔径为0.1、0.25、0.5、2.0 mm的筛子进行筛砂,取得实验所需的砂样[13]。再用清水将砂样冲洗(直至砂样上方的水变清澈)并自然风干,制成满足实验要求的土样。装样前在砂柱底部过滤筛板上放一层铁丝筛网,防止砂样渗漏。然后按密度1.6 g/cm3将砂样分层装入砂柱中,每次称取一定量砂样(3～5 cm厚),用捣棒将其压实。如砂柱中出现气泡或者裂隙,密度不均,则需要倒出重装,保证槽内样品均匀,以满足实验要求。砂柱装满后在砂样上方放一层铁丝筛网,放上滤筛板,将砂柱用盖子封好。

2 实验结果及分析

2.1 实验结果

实验前根据装砂的体积以及砂体饱水时注入蒸馏水的体积计算中砂介质的孔隙度。实验过程中水温基本上在10 ℃之间变化,因此水的运动黏度近似为0.01 cm2/s。实验中的相关参数见表1。

表1 3种介质下相关的实验参数

针对3种不同粒径的石英砂分别进行渗透实验。由于细砂的流量比较小,所以每2 min测1次流量;中砂每40 s测一次;粗砂的粒径最大,流速也最大,每10 s测1次流量。每种介质中分别进行水头差为12、22、32、42、52、62、72 cm的7组水力梯度实验。每组实验重复测5次。所得实验结果见表2—表4。

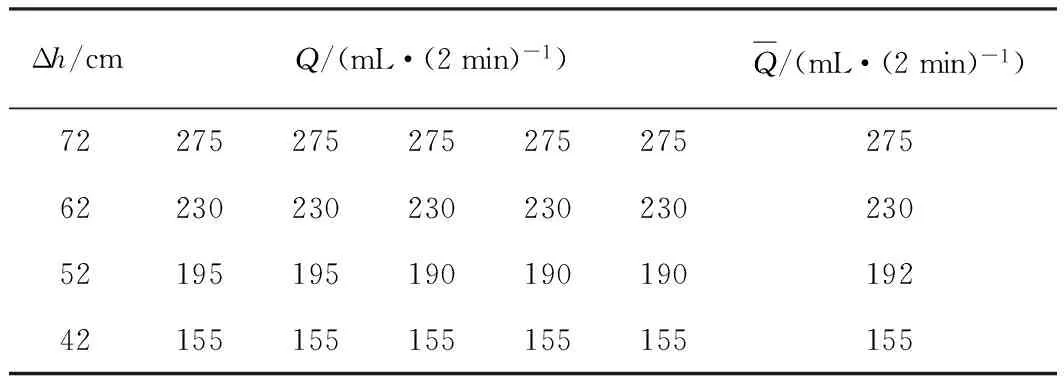
表2 细砂流量Q与水头差△h实验数据表

表2(续)

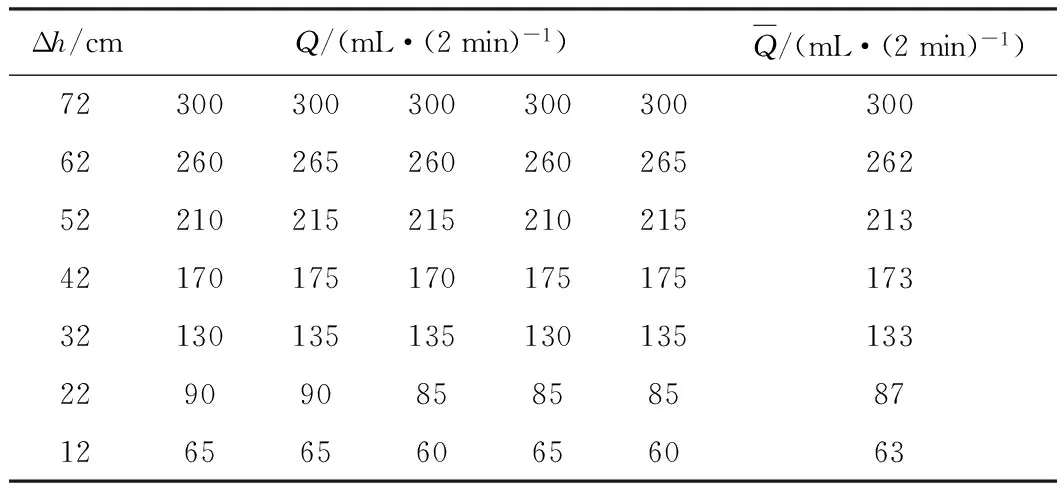
表3 中砂流量Q与水头差△h实验数据表

表4 粗砂流量Q与水头差△h实验数据表

根据达西定律、雷诺系数计算公式等对不同水力梯度下的实验数据进行计算:

其中,I为水力梯度;Re为雷诺数;K为渗透系数;v为渗流速度;Δh为水头差;ΔL为渗透路径;d为多孔介质中固相颗粒的平均粒径;ν为水的运动黏度;A为砂柱横截面积;Q为渗流量。根据上述公式计算得到的参数值见表5—表7。

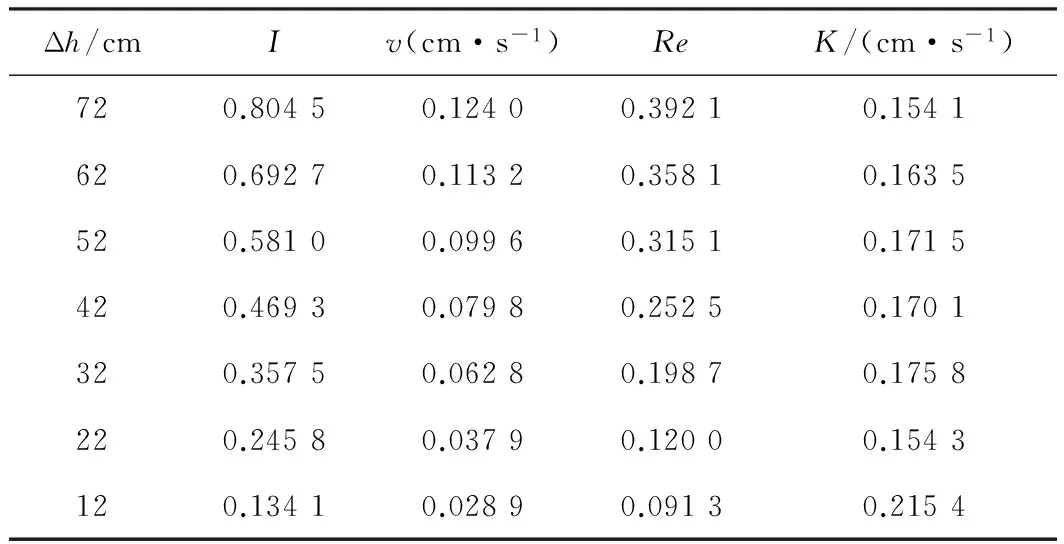
表5 粗砂参数表

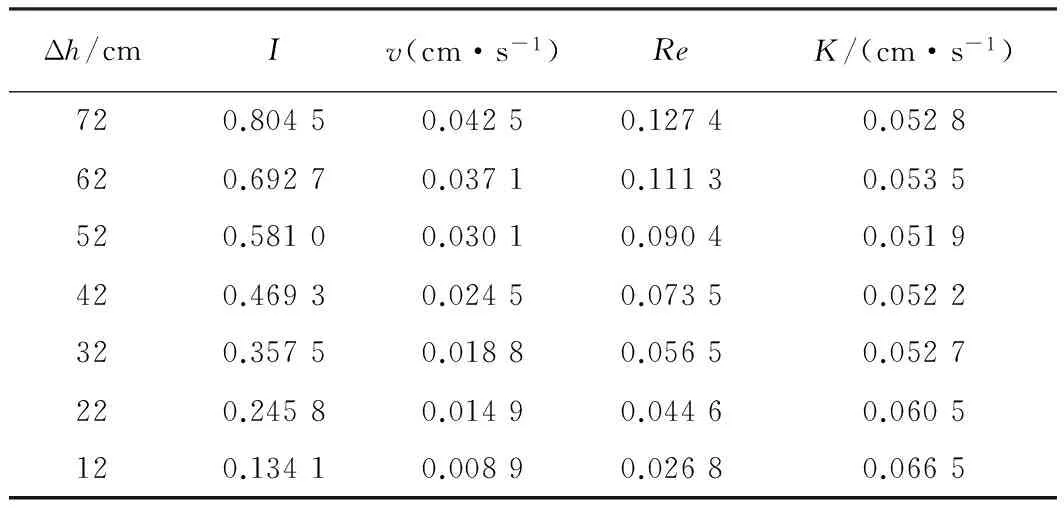
表6 中砂参数表

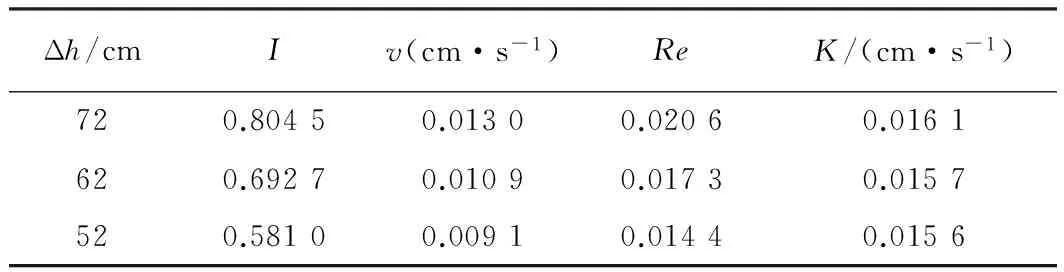
表7 细砂参数表

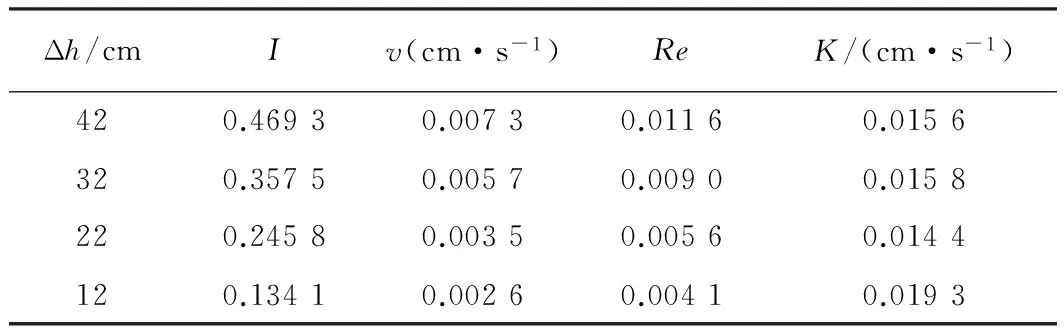
表7(续)

2.2 数据处理与分析

根据表5—表7中数据,分别作粗、中、细砂的渗透速度v与水力梯度I的关系曲线,如图2—图4所示。

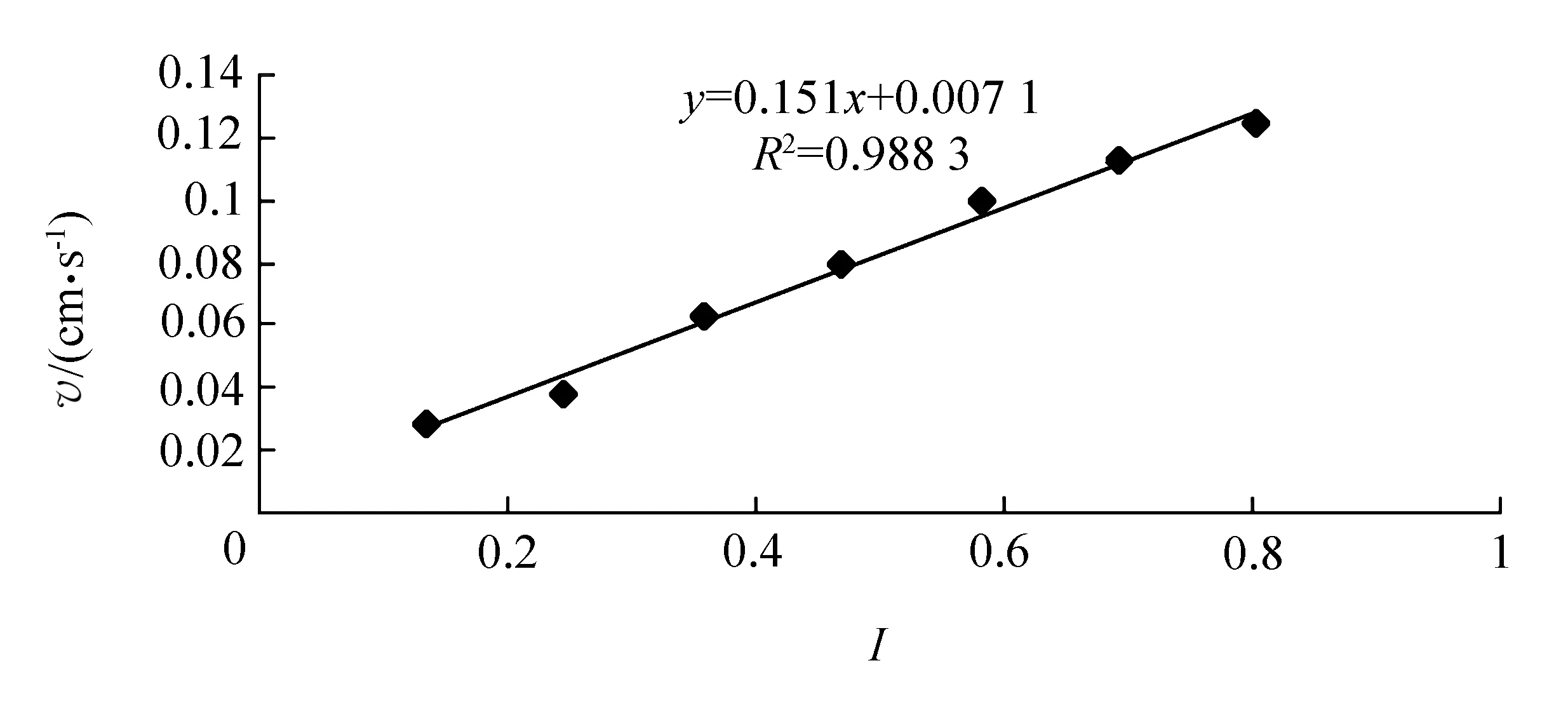
图2 粗砂渗透速度v与水力梯度I关系曲线

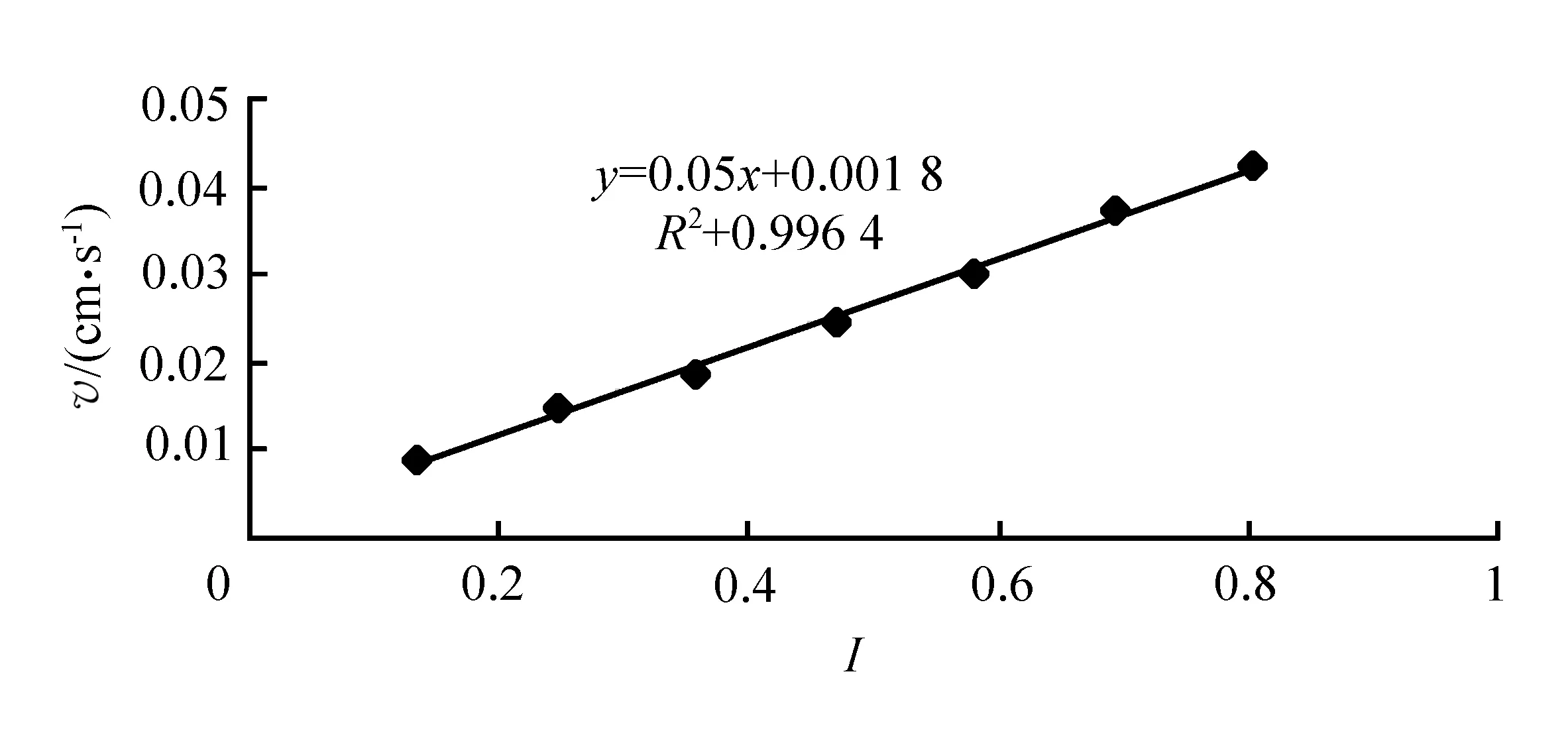
图3 中砂渗透速度v与水力梯度I关系曲线

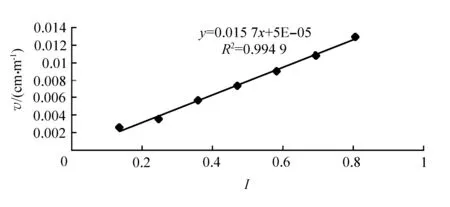
图4 细砂渗透速度v与水力梯度I关系曲线

从图中可看出，当流速很低时,渗透流速与水力梯度成线性关系,且R2均大于0.99,线性拟合结果可靠[14]，证明实验服从达西定律：v=KI,本文采用达西定律计算是合理的。但从图中数据可知，v、I并不成严格的线性关系,K值仍然存在较小的变动值。图5—图7是渗透系数K与水力梯度I的关系曲线。

由不同粗细的砂的K-I关系曲线可知：当水力梯度很小时粗砂、中砂、细砂中渗透系数都随着水力梯度的增大按一定的规律递减；在水力梯度小于0.25时,渗透系数K变化幅度较大；随着水力梯度增大,渗透系数的变化逐渐减小,K值基本趋于稳定。

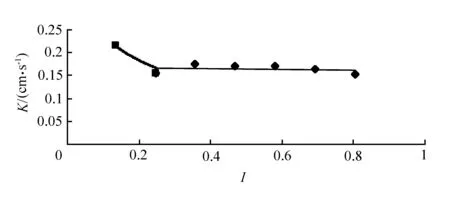
图5 粗砂渗透系数K与水力梯度I关系曲线

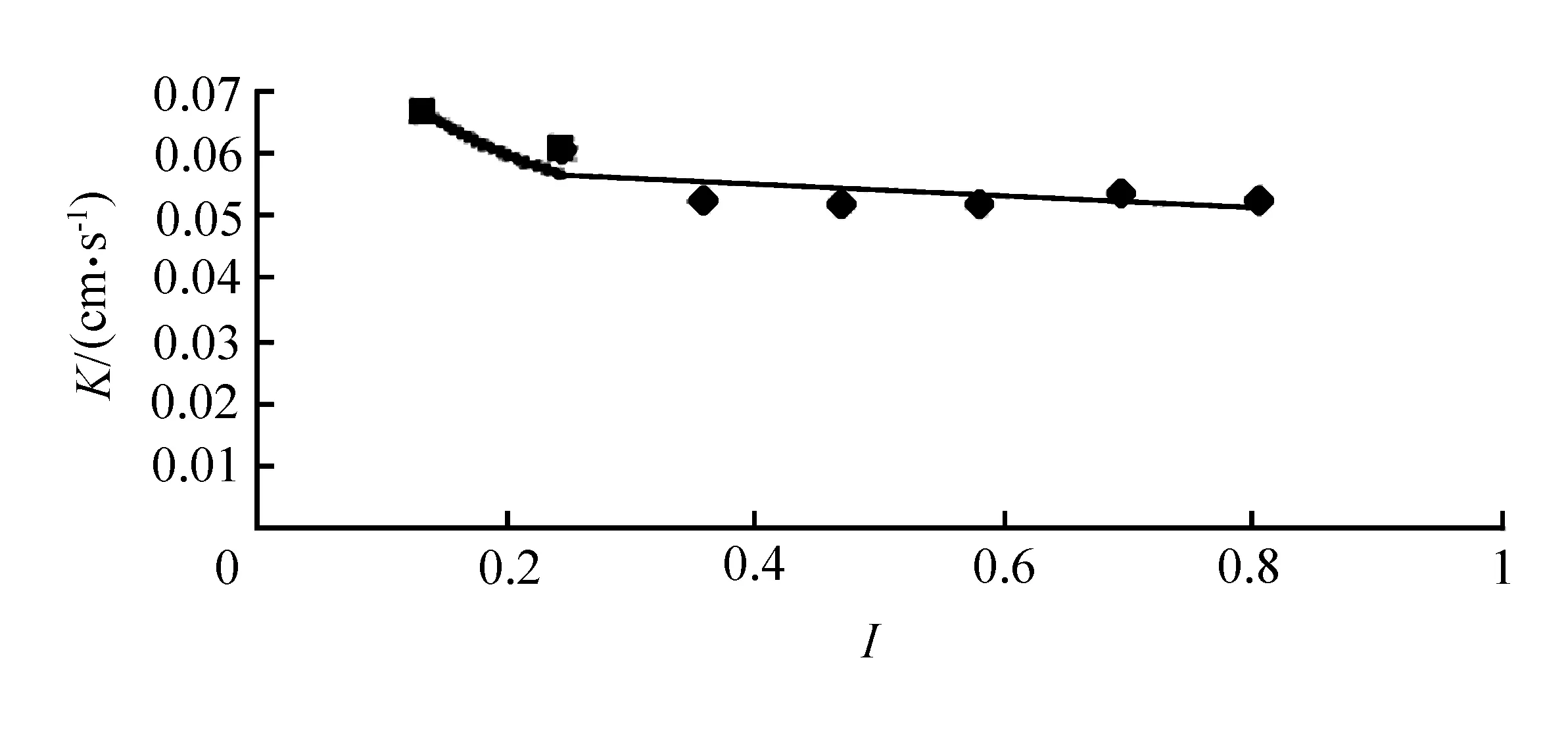
图6 中砂渗透系数K与水力梯度I关系曲线

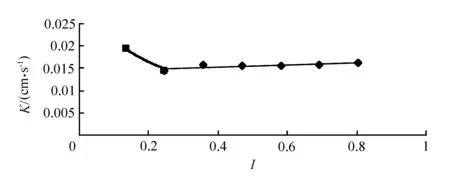
图7 细砂渗透系数K与水力梯度I关系曲线

2.3 砂粒粗细对渗透系数的影响分析

为了比较水力梯度对粗砂、中砂、细砂渗透系数的影响,利用实验获得的数据将3种介质中渗透系数相对变化率的绝对值与水力梯度I的关系进行作图比较,见图8。从图8可以看出,粗砂的渗透系数变化率最大,因此粗砂介质中水力梯度对渗透系数的影响最大,而细砂的渗透系数变化率最小。由此可知，不同水力梯度下渗透系数受粗砂的影响最大,中砂次之,细砂最小。另外从图8中可以看出，在水力梯度小于0.25时对渗透系数的影响较大(渗透系数的变化率的绝对值维持在10%以内),而当水力梯度大于0.25时对渗透系数的影响较小。

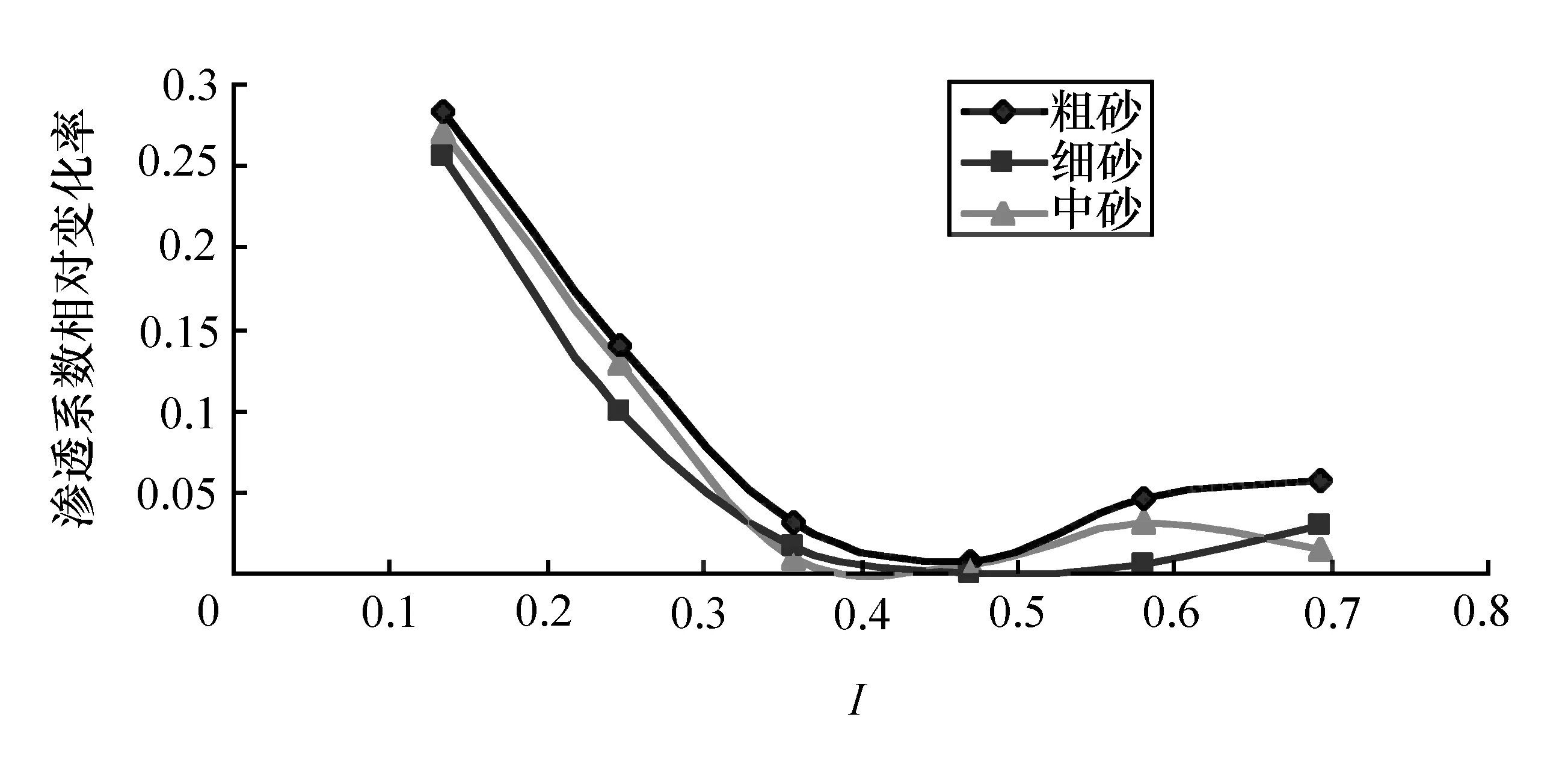
图8 渗透系数相对变化率的绝对值与水力梯度I关系图

3 结论

实验结果表明,渗透系数确实受水力梯度的影响而产生变化。由实验得到以下结论:

(1) 当水力梯度较小时,随着水力梯度的增大,渗透系数逐渐减小;

(2) 渗透系数的变化速率随着水力梯度的不同而不断变化,水力梯度小于0.25时渗透系数的改变较大,当水力梯度大于0.25时渗透系数基本稳定;

(3) 粗砂介质中水力梯度对渗透系数的影响最大,中砂次之,细砂对渗透系数的影响最小。

实验充分证明了渗透系数与水力梯度以及介质特性有关。明确水力梯度对渗透系数产生的影响对研究地下水的渗透过程有着重要的意义。由于实验室环境限制，实验水头差范围还不够大,而且实验仅就水力梯度对渗透系数的影响进行了定性的分析,二者之间的定量关系仍有待于进一步的实验验证。

References)

[1] 薛禹群,吴吉春.地下水动力学[M].3版.北京:地质出版社,2010.

[2] 桂春雷,石建省,刘继朝,等.含水层渗透系数预测及不确定性分析耦合模型[J].水力学报,2014,45(5):521-528.

[3] 张人权,梁杏,靳孟贵.水文地质学基础[M].6版.北京:地质出版社,2011.

[4] 邱珍锋,卢孝志,伍应华.考虑颗粒形状的粗粒土渗透特性试验研究[J].南水北调与水利科技,2014,12(4):102-106.

[5] 张家发,焦赳赳.颗粒形状对多孔介质孔隙特征和渗流规律影响研究的探讨[J].长江科学院院报,2011,28(3):39-44.

[6] Liu Yangsheng,Bai Qingzhong,Nie Yongfeng.Properties of Bentonite Enhanced Loess and Laterite[J].Chinese Journal of Chemical Engineering,2004,21(1):37-41.

[7] 宿辉,王晓伟,石明宇.砂砾土孔隙特征对渗透系数的影响研究[J].河北工程大学学报:自然科学版,2013,34(4):82-86.

[8] 屈智炯.对粗粒土渗透变形研究的进展[J].水电站设计,2008,24(1):48-55.

[9] 邓英尔,黄润秋,刘慈群.非饱和低渗透黏土非线性渗流定律与固结[J].水动力学研究与进展,2009,1(1):99-105.

[10] 徐德敏,黄润秋,虞修竟.高压小水力梯度岩石渗透性测试[J].岩土力学,2010,31(4):1104- 1107.

[11] Timothy T Eaton.On the importance of geological heterogeneity for flow simulation [J].Sedimentary Geology，2006,184:187-201.

[12] 刘凯,文章,梁杏,等.一维低渗透介质非达西渗流实验[J].水动力学研究与进展,2013,28(1):81-87.

[13] 中华人民共和国水利部.GB/T50123—1999 1999土工试验方法标准[S].1999.

[14] 樊贵盛,邢日县,张明斌.不同级配砂砾石介质渗透系数的试验研究[J].太原理工大学学报,2012(3):373-378.

Research on influence of different hydraulic gradient on hydraulic conductivity

Wang Fugang1, Zhang Jiahui1, Yu Jiyang2, Xu Jing1

(1. College of Environment and Resources,Jilin University,Changchun 130021, China;2. Liaoning Chemical Geology Exploration Institute, Jinzhou 121007, China)

The hydraulic conductivity is an important hydrogeological parameter.The experiment is conducted on the hydraulic conductivity to find the effect of hydraulic gradient through the laboratory test.In the experiment the coarse sand,the medium sand and the fine sand are sieved out to conduct the different hydraulic experiments. Collecting and organizing the data are to develop the relationship between the hydraulic conductivity and the filtration parameter through the computer.This article develops the rule of hydraulic conductivity which is changed with hydraulic gradient,in order to explore the variation of the hydraulic conductivity under the normal temperature and pressure.

hydraulic conductivity; hydraulic gradient; seepage velocity

2014- 12- 23

国家自然科学基金资助项目(41172205)

王福刚(1975—),男,辽宁瓦房店,博士，副教授,主要从事水文地质与环境地质研究

张佳慧(1990—),女,吉林通化,硕士研究生,现主要研究方向是地下水多向多组分反应性溶质运移、地下水循环特征.

E-mail：771731083@qq.com

TV41

B

1002-4956(2015)6- 0025- 04