一种低功耗的振弦式传感器测频系统设计*
2015-03-27何华光凌朝善玉丹丹谢开仲
何华光,凌朝善,玉丹丹,谢开仲
(1.广西大学 计算机与电子信息学院,广西 南宁530004;2.广西大学 土木建筑工程学院,广西 南宁530004)
0 引 言
振弦式传感器输出频率的变化能够反映应力的变化,具有结构简单,测量精度高,性能可靠等优点,在桥梁大坝上得到了广泛的应用[1]。在野外桥梁建设初期,由于配套市电供应系统尚未完善,使用振弦式传感器对桥梁长时间实时监测变得困难。为此,便携式低功耗振弦式传感器测频系统显得十分必要。
振弦式传感器被激振后输出信号幅度十分微弱,持续时间短,加上外部噪声的干扰,使得信号的测频变得困难[2]。通常使用较高的激振电压来提高传感器输出信号的幅度,激振电压一般大于100 V[3]。因此,激振电路是测频系统中消耗电能最大的模块。要实现系统的低功耗,降低激振电压的同时保证测频的有效性是关键。本文设计的振弦式传感器测频系统以ARM 处理器STM32L152 为核心,采用Rife 与Quinn 算法对微弱信号进行频率检测,能够极大地降低激振电压,实现系统的低功耗、高精度测频。
1 系统硬件设计
系统采用超低功耗ARM 处理器为核心,系统框图如图1 所示。

图1 硬件系统结构框图Fig 1 Structure block diagram of hardware system
STM32L152VB 是ST 公司最新推出的超低功耗微处理器,具有128 kB 的Flash,16 kB 的SRAM,32 MHz 的主频以及多种低功耗休眠模式。系统在STM32L152 的控制下对传感器进行激振,输出信号经过放大、滤波后由微处理器自带的12 位A/D 转换器进行采样,数据经过程序处理后输出结果在液晶显示屏上。系统也可根据需要将结果进行存储或者通过蓝牙模块上传到计算机。
1.1 激振电路设计
激振电路在微处理器的控制下,输出一个高电压对传感器进行激振,具体电路如图2 所示。
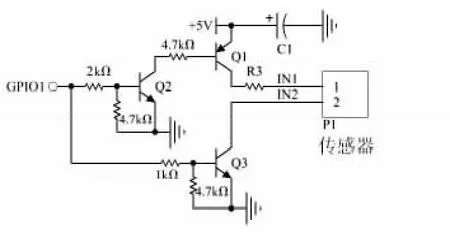
图2 激振电路Fig 2 Excitation circuit
P1 为传感器接口,R3 为限流电阻器。当微处理器GPIO 口输出高电平时,三极管Q1,Q2,Q3 导通,电源电压加载到传感器上;反之,GPIO 口输出低电平三极管截止,传感器掉电。此时,传感器输出一个与应变力相关的频率信号。为减少电路待机时消耗的电流,三极管选用漏电流小的型号。
1.2 放大电路设计
振弦式传感器被激振后,输出的频率信号十分微弱,需要进行高增益放大。具体电路如图3 所示。

图3 仪表放大电路Fig 3 Instrumentation amplifier circuit
放大器选用ADI 公司的低功耗仪表放大器AD8422。该芯片是AD620 发展到第三代的产品,具有更高的动态范围和更低的功耗。电路设计的放大倍数为1000 倍。由于振弦式传感器的激振回路和信号输出回路是共用的,输入回路中加入电阻器和二极管构成的限幅网络,避免了激振电压对放大电路的影响,同时又不影响传感器正常频率信号的输出。
1.3 滤波电路设计
传感器输出的频率信号范围从400 Hz ~6 kHz 之间。由于该信号非常微弱,容易受到外部噪声的干扰,传统的振弦式传感器测频系统一般会采用8 阶低通滤波器和8 阶高通滤波器串联的方式滤除外部噪声干扰。滤波后的信号经过整形电路,将正弦波转换为矩形波后接入微处理器相应端口。由于设计的系统采用A/D 转换、数字信号处理的方式实现传感器的频率测量,因此,系统对滤波器电路进行了简化,具体电路如图4 所示。

图4 滤波电路Fig 4 Filtering circuit
由图4 可见,滤波电路由传统的两级8 阶串联简化为两级4 阶串联,并且省去了整形电路。信号添加直流偏置后直接接入微处理器的A/D 转换端口。这样使得硬件电路复杂度显著降低,减少了电能消耗。电路使用高精度、低功耗运算放大器AD8542,该芯片内部仅消耗90μA 的电流。
1.4 电源电路设计
运算放大器使用的负电压由LM2663 芯片产生,该芯片为开关电容/电压转换器,可将输入的正电压转换为大小相等的负电压。正电压采用超低静态电流3.3V 稳压芯片TPS78233DDCR,该芯片静态电流仅为0.5μA。当其使能端EN 为低电平时,芯片可关断电源输出。利用这个功能,微处理器结合多个电源芯片可以实现系统的动态电源管理。需要工作的模块才能上电,其他模块电源应该处于关断状态,以节约电能。具体电路如图5 所示。

图5 电源电路Fig 5 Power circuit
2 系统软件设计
2.1 Rife 算法与Quinn 算法基本原理
系统采用Rife 算法与Quinn 算法结合实现振弦式传感器的精确测频。Rife 测频算法指出,白噪声背景中某一正弦信号的频率估算如式(1)[4]

式中 N 为采样点数,fs为采样频率;k0为FFT 后最大谱线离散频率索引值;|X(k0)|为最大谱线的幅度;|X(k0+r)|为k0相邻的次大谱线幅度;Rife 算法在信噪比较差的情况下会出现插值方向错误,这个错误在式(1)中具体表现就是r 本应取值为正1,算法判断为负1,或者是相反的情况,这造成频率估计产生较大的误差。Quinn 算法利用信号的相位信息可以弥补了这一缺陷。因此,Rife 算法与Quinn算法结合可以实现在复杂噪声环境下频率的精确测量[5]。
2.2 系统软件流程
系统的状态迁移图如图6 所示。

图6 系统状态迁移图Fig 6 Transition graph of system state
由图6 可见,系统在测量频率结束后立即进入休眠模式,而后在RTC 实时时钟控制下定时唤醒进入工作模式,从而实现振弦式传感器无人值守、周期性定时测量的目的。此外,系统也可通过按键唤醒实现单次测量。系统工作流程如图7 所示。

图7 软件流程图Fig 7 Flowchart of software
系统先采用一个200 ms 的单脉冲电压对传感器激振,测得一个粗略的频率f。然后再用频率为f 的PWM 波对传感器进行二次激振,此时传感器由于内部钢弦产生共振,输出较大幅度的正弦波信号。这种二次激振的方式有利于提高测量精度[6]。
3 测试实验
3.1 系统功能测试
通过函数信号发生器将幅度为1 mV 的正弦波接入系统,测得的数据如表1 所示。

表1 正弦波测量结果Tab 1 Measurement results of sine wave
从表1 可以看出:系统能够以较高的精度实现微弱信号的频率测量,相对误差低于0.025%。
为对比系统在高压激振与低压激振时的性能差异,将连接导线为10 m 的振弦式传感器接入系统,同时改变系统的激振电压,得到数据如表2 所示。

表2 高压、低压激振数据对比Tab 2 High voltage,low voltage excitation data comparison
1#测量值是激振电压为24 V 时测量得到的数据,2#测量值是激振电压为5V 时测量得到的数据,由表2 可以看出:由于传感器的机械容差,每次测量结果有很小的差别。但是系统在两种激振电压下,连续测量7 次的平均值非常相近。这说明系统在5V 激振电压下也能可靠的工作,得到正确的结果。
3.2 系统功耗测试
为测量系统动态功耗,搭建检测系统电流的硬件模型如图8 所示。

图8 系统测试模型Fig 8 System test model
在测频系统的电源回路中串联一个0.1 Ω 的采样电阻器,电阻器上的电压被放大50 倍后接入示波器。在示波器上观察到的系统电流波形如图9 所示。

图9 系统动态电流波形Fig 9 Dynamic current waveform of system
结合程序流程图,图9 中T1时间段为单脉冲激励200 ms,T2时段320 ms 包含了延时等待、A/D 采样与算法运行时间,T3为PWM 激励100 ms,T4时段380 ms 包含延时等待、第二次A/D 采样以及算法运行时间。T5时间段由微处理器控制系统进入休眠状态,消耗电流仅为15 μA,可忽略不计。整个测频周期耗时1s,系统平均电流为图9 曲线对时间的积分。可由式(2)进行简化运算

经计算,系统一个测频周期的平均电流为23.2 mA。在不存储、发送数据的情况下,一个10000 mAh 的手机移动电源可供本系统完成150 万次测量。实验室条件下,每分钟测频一次,系统可以使用大约3 个月。
4 结 论
本文研究了振弦式传感器的低功耗设计,利用Rife 与Quinn算法,在ARM处理器上实现了振弦式传感器频率信号的低功耗、高精度测量。实验结果表明:系统能够在平均工作电流仅为23.2 mA 的条件下,实现相对误差低于0.025%的振弦式传感器精确测频。系统休眠状态下消耗电流仅为15 μA,特别适合振弦式传感器在无市电情况下对桥梁等大型建筑的长期监测。
[1] 莫 琳,何华光.多路振弦式传感器桥梁检测系统设计[J].传感器与微系统,2014,33(4):68-71.
[2] 高 友.振弦式传感器测量过程中干扰问题的解决[J].仪表技术与传感器,2007(2):54-55.
[3] 高 友.振弦式传感器测量过程中干扰问题的解决[J].仪表技术与传感器,2007(2):54-55.
[4] Rife D C,Vincent G A.Use of the discrete Fourier transform in the measurement of frequencies and levels of tones[J].Bell Syst Tech J,1970,49:197-228.
[5] 朱 磊,董 亮,刘树东.基于Quinn 算法与改进的Rife 算法的正弦信号频率估计[J].大庆石油学院学报,2010(1):98-101,121.
[6] 贺 虎,王万顺.振弦式传感器激振策略优化[J].传感技术学报,2010(1):74-77.
