多选择背包问题离散狼群算法研究*

董亚科，杜 军，李 博，丁 超

(空军工程大学 航空航天工程学院，陕西 西安710038)

0 引 言

多选择背包问题是经典的NP 难问题，现实中的很多问题都是以多选择背包问题为背景而建模的。因此，对该类的研究具有重大理论意义和应用价值。目前对NP 难问题已经提出如人工鱼群算法、启发式算法、粒子群算法、遗传算法等诸多方法［1～10］，但在大规模约束条件下这些算法很难获得最优解。狼群算法在多维多峰值连续函数寻优方面取得了很好效果［11］，如何将狼群算法扩展到离散领域，准确地找到最优解，在研究狼群算法和多选择背包问题两方面都具有重要意义。

本文提出的一种求解多选择背包问题离散狼群算法(discrete wolf pack algorithm，DWPA)通过采用遗传算法编码规则，把人工狼引入到了离散领域。利用学习机制，使得人工狼优秀基因得到继承，实现了人工狼之间的交流，保证了离散狼群算法的收敛性，通过人工狼的“强者生存”群体更新策略，保留了最优个体，增加了搜索的多样性，猛狼奔袭采用了自适应步长，加快了算法收敛速度。

1 多选择背包模型

多选择背包问题有如下定义:有一个载重重量一定的背包和一批要放进该背包具有一定价值和重量的物品，这些物品首先被分为相互排斥的若干类，每一类中有若干个不同物品。从每一类物品中取一个物品放入背包中，在背包内的物品重量在不超过背包载重前提下，使背包内物品价值总和最大。对该问题的数学描述如下

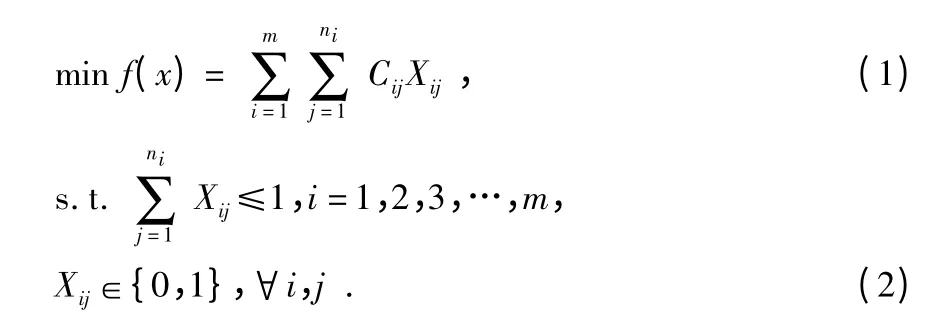
其中，i 为不同分类的下标，j 为每一类中不同物品的下标，ni为第i 类物品的数量，cij为第i 类中第j 个物品的价值。m 为不同分类的数量，Wij为第i 类中第j 个物品的重量，w 为背包的载重，当Xij=1 时，表示第i 类中的第j 个物品放入背包;当Xij=0 时，表示第i 类中的第j 个物品不放入背包。

2 狼群优化算法

狼群过着群居且分工明确的群居生活，根据职能的不同，人工狼分为头狼、探狼和猛狼。头狼:头狼是狼群中的首领，它不断地根据狼群所感知的信息进行决策，指挥狼群尽快的捕捉到猎物。探狼:寻找猎物时，狼群会派出几只敏锐的探狼在猎物活动范围内随机寻找，根据猎物气味的浓度进行决策，浓度越高表明离猎物越近。猛狼:当探狼发现猎物后会立即报告给头狼，头狼通过嚎叫召唤周围的猛狼对猎物进行围攻，猛狼闻声会朝着该探狼奔袭，向猎物靠近，狼群算法流程如图1。

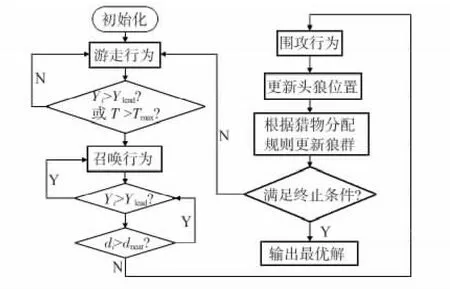
图1 WPA 流程图Fig 1 Flow chart of WPA

狼群算法具体步骤:

1)初始化狼群种群中个体数目N，最大迭代次数kmax，探狼比例因子α，最大游走次数Tmax，种群更新比例因子R等。

2)选择最优个体为头狼，除头狼外的S_num 人工狼为探狼并执行游走行为，直到某只探狼感觉到的猎物气味浓度Yi大于头狼所感知的猎物气味浓度Ylead或达到最大游走次数。

3)猛狼奔袭:若途中猛狼感知的猎物气味浓度Yi＞Ylead，则Yi=Ylead，替代头狼发起召唤行为;若Yi＜Ylead，则猛狼继续奔袭直到距离猎物的距离小于阈值dnear。

4)对参与围攻的人工狼位置进行更新。

5)挑选出距离猎物最近的人工狼代替头狼，完成对头狼的更新，并按照种群更新比例因子对群体进行更新，淘汰距离猎物较远的人工狼。

6)判断是否达到最大迭代次数Tmax或精度要求，若达到要求，则输出头狼位置;否则，转至步骤(2)。

3 离散空间的DWPA

DWPA 关键问题是人工狼位置的更新的表示，同时，根据离散量的特点定义人工狼位置更新的运动方程。设狼群的捕猎空间为一个M×N 的空间，其中，M 为狼群中人工狼数目，N 为要寻优的变量数。人工狼i 的状态可表示为:Xi=［Xi1，Xi2，…，XiN］，其中，XiN为第i 匹人工狼在欲寻优的第d(d=1，2，3，…，N)维变量空间中的位置;人工狼所感知到的气味浓度为y=f(x)，其中，y 就是要寻优的目标函数。

3.1 人工狼的位置

每个人工狼染色体定义为按一定规则编码的个体，遗传算法中的一个染色体相当于狼群算法中的一个人工狼，设有M 个人工狼组成一个群体，第i 个狼表示一N 维的向量Xi=［Xi1，Xi2，Xi3，…，XiN］，i=1，2，3，…，M，即第i 个狼在空间中的位置是Xij。本文编码方式采用正整数编码。在正整数编码方式中，种群中每一个人工狼的染色体由N个基因组成，分别对应着N 个不同的分类，其中第i 个基因是从集合Ni(Ni为第i 类所有物品编号所构成的集合{1，2，…，ni})中任意选取的一个正整数，即基因在染色体中的位置用来表示选取的物品所在的类的编号，而基因值则表示物品在该类中的编号。

图2 为人工狼的染色体。

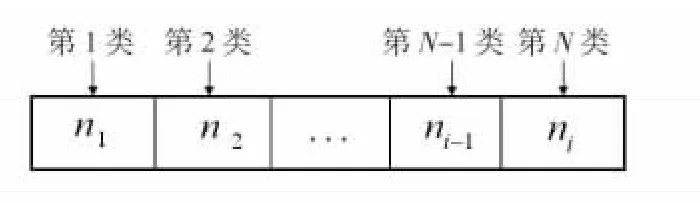
图2 编码规则Fig 2 Coding rule

3.2 学习机制

狼群算法应用在离散空间的关键问题是解决人工狼位置更新的表示，学习机制是一种向精英个体不断学习的行为，使精英个体的优秀基因得到继承，以此完成向头狼的奔袭，人工狼向优秀个体学习的过程，是人工狼不断向头狼靠拢的过程。当头狼发起召唤，人工狼向头狼奔袭时，随机选择头狼染色体上的若干编码，赋给对应位置上的该人工狼的染色体，这样有利于开辟新的解，防止早熟而陷入局部最优。

3.3 位置更新机制

本文通过引入学习机制，重新设计了狼群算法中人工探狼游走、猛狼奔袭和群狼围攻过程。

1)人工探狼游走:当前头狼位置为感受猎物气味浓度最高的人工狼。假设人工探狼Yi的染色体编码［Xi1，Xi2，…，XiN］，利用遗传算法中染色体基因的变异思想，随机对每个人工探狼染色体的个编码进行变异操作，然后计算探狼Yi当前位置的猎物气味浓度，如果当前猎物气味浓度大于头狼所感知的气味浓度，表明猎物离探狼Yi的位置更近且该探狼最有可能捕获猎物，于是探狼Yi代替头狼并发起召唤行为，即Ytead=Yi。

探狼游走步长定义如下

其中，λ∈［0，1］，L 为编码长度。

2)人工猛狼奔袭:假设人工猛狼的染色体编码为［Xi1，Xi2，…，XiN］，头狼发起召唤行为后，猛狼i 以较大步长向头狼的位置奔袭。利用学习机制，采用自适应步长，选择头狼染色体的个编码，用这个编码替换猛狼对应的位置上的编码，完成猛狼i 向头狼Ylead位置的奔袭，奔袭途中，若猛狼i 感知到的猎物气味浓度Yi＞Ylead，则Ylead=Yi，该猛狼转换为头狼并发起召唤行为;若Yi＜Ylead，则该猛狼继续向头狼奔袭直到其与头狼嗅到的猎物气味浓度的差值小于某阈值P 时加入到对猎物的围捕。

自适应奔袭步长定义如下

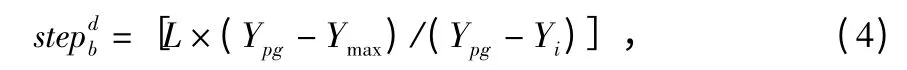
式中 L 为编码长度，Ypg为当前狼群中最大的猎物气味浓度，Ymax为当前猛狼中最大的猎物气味浓度，Yi为猛狼i 嗅到的猎物气味浓度。

3)人工狼围捕:当其它人工狼嗅到的食物气味浓度和头狼嗅到的食物浓度之差小于设定的阈值P，狼群展开围捕行为。在人工狼的新的围捕策略中，即对每个人工狼的染色体［Xi1，Xi2，Xi3，…，XiN］，利用学习机制，随机选择染色体一个编码，将当前头狼染色体对应位置上的编码赋到该人工狼的染色体的对应位置上，实现对猎物的围捕

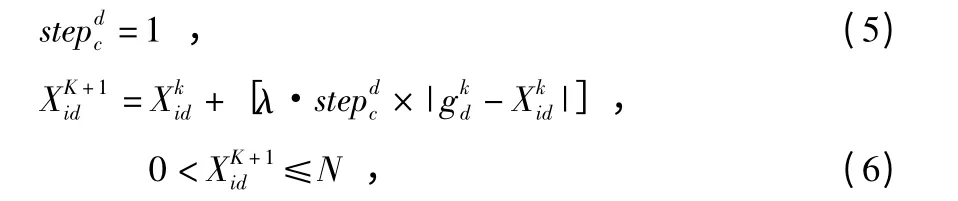
4 仿真实验

4.1 DWPA 求解多选择背包问题

为了说明本文提出的求解多选择背包问题的DWPA的有效性，采用文献［12］中提出的一个含有8 类物品的多选择背包问题典型例子进行仿真实验，文献［12］中设置种群规模为40，迭代次数为100 次，进行40 次运算，找到最优解34 的概率为67.5%

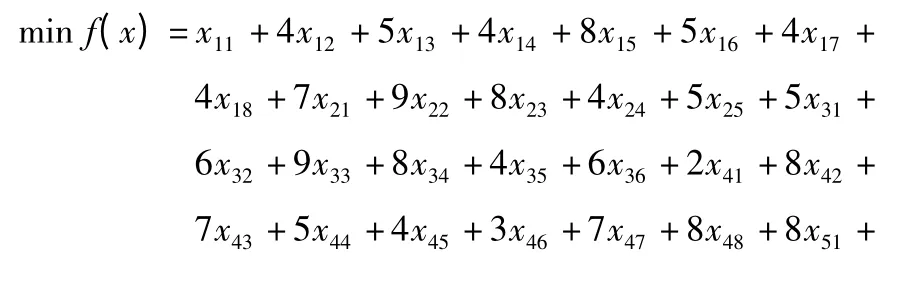
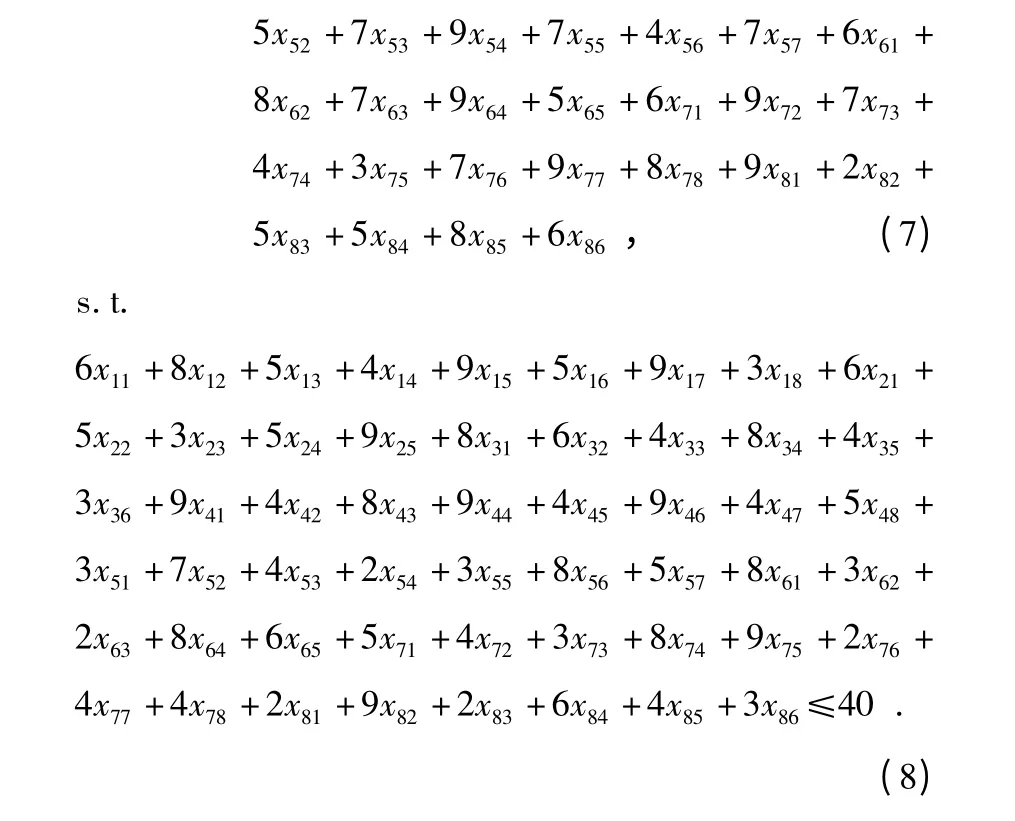
表1 表示不同迭代次数下DWPA 找到最优解34 的概率，DWPA 的准确性明显优于遗传算法。

表1 不同迭代次数下DWPA 找到最优结果的准确率Tab 1 Accuracy of DWPA finding the optimal result under different number of iterations

4.2 离散空间的DWPA 自适应步长测试

针对文献［12］提出的多选择背包问题，表2 记录运行次数均为100 次，求得最优解34 时的平均迭代次数。从表中可以明显看出:自适应步长的平均迭代次数和运行时间少于其他步长的平均迭代次数和运行时间，说明了自适应步长的有效性。

表2 不同步长时找到最优解时的平均迭代次数Tab 2 Average number of iterations finding the optimal solution of different step length

5 结 论

以求解多选择背包问题为例，提出了一种基于离散空间的DWPA 的具体实现，DWPA 中使用了自适应步长，增加了搜索效率。采用了学习机制，有效实现人工狼的交流，使算法在搜索效率和搜索精度方面得到提高。仿真实验表明:DWPA 具有非常好的性能，能够成功应用到NP－hard 等组合优化问题领域。

［1］ Sun Youfa，Gao Jingguang，Zhang Chengke，et al.Chaotic genetic algorithm with feedback and its applications to constrained optimization［J］.Journal of South China University of Technology:Natural Science Edition，2007，35(1):19－23.

［2］ Frevile A.The multi－optional 0－1knapsack problem:An overview［J］.European Journal of Operational Research，2004，155(1):1－21.

［3］ Gen M，Cheng R，Wang D.Genetic algorithm for solving shortest path problems［C］∥IEEE International Conference on Evolutional Computation，Piscataway:IEEE，1997:401－406.

［4］ Andonov R，Poirriez V，Rajopadhye S.Unbouned knapsack problem:Dynamic program revisited［J］.European Journal of Operational Research，2000，123(2):394－407.

［5］ Yuan Liwei，Liu Fuxian，Zhao Baojun.Improved GA and its application to knapsack problem［J］.System Engineering and Electronics，2005，27(4):718－719.

［6］ Hong Baojiang，Yang Qigui.Fast solution algorithm of multiple choice knapsack problem［J］.Journal of South China University of Technology:Natural Science Edition，2009，37(4):42－45.

［7］ 陈 娟，王志刚，夏慧明.粒子群优化算法求解多选择背包问题［J］.价值工程，2012，2(5):197－198.

［8］ 叶宇风.多重群体遗传算法在多选择背包问题中的应用［J］.计算机工程与设计，2005，26(12):3442－3444.

［9］ Lu Haiyan，Chen Weiqi.Dynamic－objective particle S－warm optimization for constrained optimization［J］.Journal of Combinational Optimization，2006，12(4):409－419.

［10］Gary M，Johnsin D.Computer and intractability:A guide to the theory of NP－completeness［M］.New York:［s.n.］，1979.

［11］吴虎胜，张凤鸣，吴庐山.一种新的群体智能算法狼群算法［J］.系统工程与电子技术，2013，35(11):2430－2438.

［12］玄光男，程润伟，于歆杰，等.遗传算法与工程优化［M］.北京:清华大学出版社，2004:56－59.