基于温度调制的气体传感器动态信号识别研究*

何爱香，唐祯安，魏广芬，余 隽

(1.大连理工大学 电信学部 集成电路技术辽宁省重点实验室，辽宁 大连116024;2.山东工商学院 信电学院，山东 烟台264005)

0 引 言

基于SnO2的气体传感器已经在气体检测方面得到了广泛的应用，比较其他气体传感器，它具有低功耗和高灵敏度等优点。但是，SnO2气体传感器由于它的低选择性、交叉敏感、传感器漂移、对环境温湿度较敏感等缺点制约了它的发展和应用。为了克服传感器的这些缺点，很多学者主要从以下3 个方面来进行改进:1)选择更好的敏感薄膜材料［1］;2)传感器阵列优化，静态和动态的温度调制加热模式的选择［2，3］;3)信号处理和模式识别算法的改进［4］。本文主要从动态温度调制加热模式的选择和信号处理这两方面来优化SnO2传感器的检测性能。

1 实验过程

在本次实验过程中，选用了自制的Pt/SnO2微热板气体传感器。取4 只提前预热好的气体传感器组成传感器阵列，对3000×10－6CH4，150×10－6CO 和15×10－6C2H5OH三种不同体积分数的工业气体进行测量。传感器加热温度调制模式选择正弦波、脉冲波、锯齿波和三角波四种加热波形，温度变换范围在200～300 ℃。对于每一种加热波形又选择了八种调制周期，分别为T=4，10，20，30，40，50，60，80 s。测试步骤为首先通入洁净空气清洗1 200 s，然后通入CH4600 s，再通入洁净空气900 s，CO 600 s，再通入洁净空气900 s，C2H5OH 600 s，最后通入洁净空气清洗900 s。实验中上述步骤循环往复，直到8 个周期全部测完。

2 实验结果与数据分析

2.1 传感器动态响应信号

图1 是调制周期为40 s 时四种温度调制模式下的输出电压信号。由图1 可以看出:气敏电阻器受加热电压的影响很大，这是因为微热板可以在ms 级的时间内达到加热电压设定的温度，即气敏电阻器的响应时间大约在3 ms 左右，而传感器对被测气体的响应时间和恢复时间由其表面的物理化学吸附和脱附导致，反应较慢。在吸附过程中最终达到稳定状态需要1～2 min 的时间，在脱附过程中传感器恢复到纯净空气中的基线值也需要大约2～3 min 的时间。所以，相对于加热电压的高频率变化，微热板的响应为强信号，而传感器对被测气体的响应表现为微弱信号。从图1中也可以看到，由于吸附和脱附时间较长，传感器对被测气体的响应主要体现在输出电压波形的包络上。

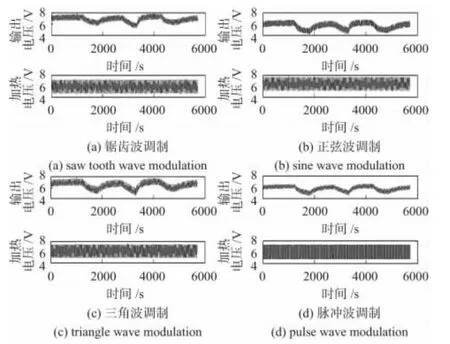
图1 输出电压和加热电压(T=40 s)Fig 1 Output voltage and heating voltage(T=40 s)

2.2 特征提取

以调制周期T=40 s 的锯齿波温度调制模式为例，将传感器的原始时域电压信号进行短时傅里叶变换(short－time Fourier transform，STFT)，窗选择汉明窗，窗的长度取原始信号长度的1/4，即N=375。得到如图2 所示的幅度谱图，从图2 中发现被测气体完成吸附和脱附的整个过程中，它的频率都非常低，只有在低频处有很大的值，随着频率的升高，幅度谱快速下降为0。所以，只需要将低频处的幅度值提取出来，就可以得到CO，CH4和C2H5OH 的主要特征信息。

在幅度谱的两侧由于加汉明窗的原因，频谱呈线性变化，为了去除汉明窗对信号的影响，在后续处理过程中，去掉频谱两端的数据，只保留中间300～1 300 s 的一段幅度值作为主要特征信息，留作后续数据处理。

2.3 周期对传感器的影响

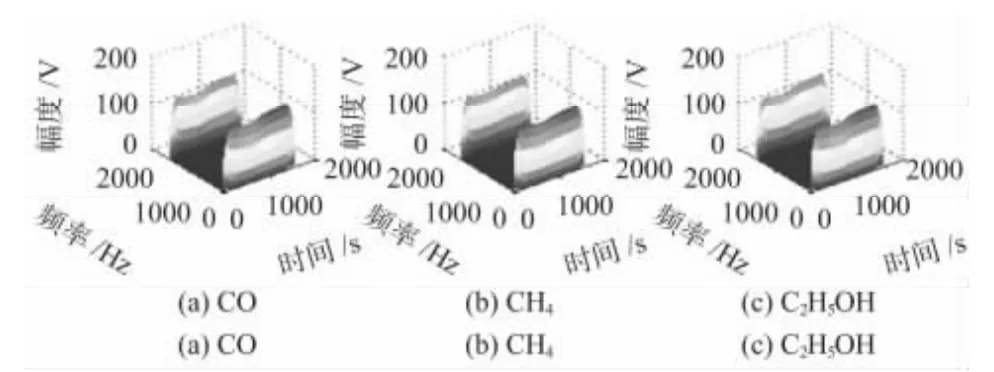
图2 被测气体的STFT 幅度谱图(锯齿波，T=40 s)Fig 2 STFT amplitude diagram of measured gas(saw tooth wave，T=40 s)

本实验将调制周期T 分别设置为4，10，20，30，40，60，80 s，以便考察温度调制周期对气体传感器灵敏度的影响。在不同的调制周期下，获得气体传感器的动态响应信号，对其进行短时傅里叶变换，提取出f=0Hz 处的直流幅度值，然后截取出其中的300～1300 s 的一段数值，进行PCA，得到图3 所示的图。

图3 PCA 分析散点图Fig 3 Scatter diagram of PCA analysis

从图3(b)看出:在四周调制波形中短时傅里叶变换和PCA 结合的算法最适合应用于正弦波调制(除去T=4 s)后的传感器响应信号。正弦波调制几乎与调制周期无关，除了周期T=4 s，其他的都集中在了一点。从图3(a)，(d)看出，锯齿波和脉冲波调制模式下，第一和第二主成分随着周期的减小呈线性变化。从图3(c)可以看出:在三角波温度调制下，第一和第二主成分受到周期的影响较大，分布也相对分散。在周期T 为40，50，60，80 s 时，三种气体的分布很集中，几乎与周期无关。但是，当周期小于40 s 时，分布零散，受周期影响较大，并且随着周期T 的增长而线性减小。所以，在选择调制周期时，若选择调制波形为三角波、脉冲波、锯齿波和正弦波，应该将调制周期T 控制在大于40 s 以上较为合适，调制频率不易过大。虽然第一和第二主成分受到了调制周期的影响，但从图3 中发现不同气体的分布仍然非常集中，所以，可以得出结论，气体种类和这八种调制周期无关。

2.4 决策树识别

在本次实验过程中，阵列由4 只传感器构成，对三种不同浓度气体进行测量。采用了八种周期调制模式，对于每一种调制波形可以获得96 个实验样本数据，其中每种被测气体的样本数据为32 个。调制波形共有四种，总的实验样本为384 个。另外，每个实验数据经过短时傅里叶变换和PCA 后，取前4 个主成分作为特征值。最后，构建成一个384×4 的总样本数据库。

由前面PCA 得知，八种温度调制周期对气体种类的影响较小，而温度调制波形对被测气体的影响很大。所以，在决策树识别过程中，不再考虑八种调制周期的影响，只分析四种调制波形的识别准确率。为了分析方便，将三种被测气体CO，CH4和C2H5OH 分别标记为第1 类、第2 类和第3 类。

对于每一种温度调制波形模式，为了防止分类过程中偶然性的出现，本文在分类过程中采用了K 折交叉验证(K－fold cross－validation)方法，将三种被测气体的样本混合，构成96×4 的样本库，将96 个样本随机分为6 份，取其中1 份为测试样本，剩余5 份作为训练样本。分类循环6 次，最后将分类准确率的平均值作为最后结果。表1 为决策树的分类准确率，包括6 次实验过程中的最高准确率、最低准确率和平均准确率。其中，正弦波调制模式的平均正确率最高，为100%，三角波的平均准确率最低，为98.06%。

3 结 论

实验结果表明:通过加热模式的使用，明显提高了气体种类的识别准确率。而本文的算法最适合正弦波的温度调制模式，其次为锯齿波和脉冲波，最差为三角波。同时，调制周期的选择不易太小，在40～80 s 较为合适。正弦波的温度调制模式下，决策树识别准确率几乎达到了100%，而其他三种调制模式，测试气体都存在误判现象。

表1 识别准确率Tab 1 Accuracy rate of recognition

［1］ Yi S.A novel approach to fabricate metal oxide nanowire－like networks－based coplanar gas sensors array for enhanced selectivity［J］.Sensors and Actuators B，2014，204:351－359.

［2］ Rakesh Gosangi，Ricardo Gutierrez－Osuna.Active temperature modulation of metal－oxide sensors for quantitative analysis of gas mixtures［J］.Sensors and Actuators B，2013，185:201－210.

［3］ Hossein－Babaei F，Amini A.A breakthrough in gas diagnosis with a temperature－modulated generic metal oxide gas sensor［J］.Sensors and Actuators B，2012，166:419－425.

［4］ Amini A，Bagheri Mohammad Ali.Improving gas identification accuracy of a temperature－modulated gas sensor using an ensemble of classiɦers［J］.Sensors and Actuators B，2013，187:241－246.