包络轨迹圆在磁场中应用的误区

李刚

带电粒子在有界磁场中的问题，在考查学生知识的同时，突出考查了学生的能力，是高考的热点，也是平常教学中的难点。在解决此类问题时，包络轨迹圆是一个行之有效的方法，但是，在应用过程中，存在一个隐蔽的错误，本文旨在探索包络圆方法在应用中的这个误区。

【模型特征】带电粒子从某一点以大小不变而方向不限定的速度射入匀强磁场中，把其軌迹连续起来观察可看出是一个半径不变的圆，这个圆与每个轨迹圆都是相切的，称为包络圆（如图1）。解题时使用圆规可以快速画出其轨迹，并且依托包络圆，快速确定粒子到达的范围，达到快速解答试题的目的。

【典例解析与误区分析】例1.在距边界L=16 cm处，有一个点状的放射源s，它向各个方向发射正粒子，正粒子的半径R为10 cm，求边界上被正粒子打中的区域的长度。

（1）速度的大小；

（2）速度方向与y轴正方向夹角的正弦。

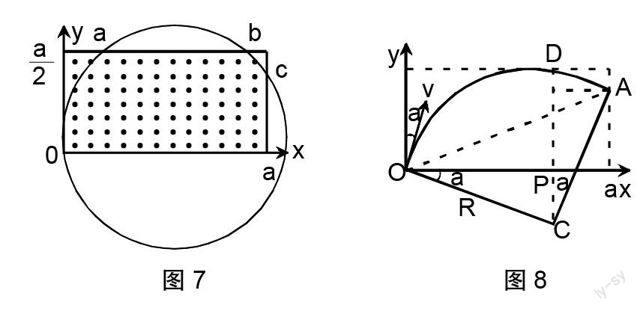
【分析】大量的粒子进入磁场后，会形成无数个轨迹圆，若取+y方向入射粒子的轨迹圆，与边界会出现三个交点a、b、c（如图7），第一个交点a即为粒子离开磁场的位置，而b、c交点实际上是不存在的，如果不考虑这个虚实交点的问题，仅仅凭借包络的圆轨迹是很容易取虚交点b或c，作出错误的分析。明确这个误区，对这个轨迹圆顺时针进行旋转，容易发现，轨迹圆与磁场上边界相切交且与右边界交于A点时，对应的弦长OA最长（如图8），从而其所对应的时间也是最长的，即为条件给出的四分之一周期。

【结论】由以上分析可知，包络圆的解法之所以存在误区，是由于忽略了轨迹与边界的虚实交点的判断，针对这种情况，单圆旋转法是破解之道，解题时，先用圆规画出单圆轨迹，并且沿着粒子运动的方向从起点开始寻找虚实交点，快速确定粒子与边界的实际交点，据此建立正确的几何关系，解决问题。

编辑 郑 淼