一种基于云模型的自适应蚁群算法

李 絮，郭 英，刘争艳

(阜阳师范学院 计算机与信息工程学院，安徽 阜阳 236041)

蚁群算法(Ant Colony Algorithm，ACA)是受自然界中蚂蚁觅食行为启发，由意大利学者Marco Dorigo 等人提出的一种仿生智能优化算法，已被广泛应用到路径规划、车辆调度、旅行商问题( TSP)等一系列组合优化问题中[1-3]。目前研究者们对蚁群算法进行了大量的改进研究，如文献[4]利用粒子群算法对蚁群算法的参数进行优化选取，设计了一种全局异步与精英策略相结合的信息素更新机制;文献[5]通过引入挥发率动态衰减机制，并重新定义启发式信息及引入边界对称变异策略，提出了一种新蚁群优化算法。虽然改进的算法的求解质量有所提高，但算法仍存在后期易陷入局部极优、收敛速度慢等问题，而其中一个关键问题是如何在“探索”和“开发”之间建立一个平衡。

云模型是由我国学者李德毅教授提出的一种定性定量之间的不确定性转换模型。近年来云模型这一不确定性处理机制也被引入到对群智能进化算法的改进中，如文献[6]利用云模型控制量子粒子群算法中关键参数，以达到对粒子寻优自适应控制的目的;文献[7]采用云模型对粒子群算法进行改进，都取得了显著效果。

本文借鉴云模型理论，提出一种新的基于云模型的自适应蚁群算法( Adaptive Ant Colony Algorithm Based on Cloud Model，CACA)。利用云模型所独具的随机性和稳定性的特点，使得提出的算法既能保持种群的多样性，改善蚁群算法对未知解的探索能力，同时又能加强蚁群算法对已知解的开发和利用，提高算法的收敛速度和求解质量。

1 基本蚁群算法

1.1 路径构建方式

以求解TSP 问题为例，蚂蚁从起点城市出发，遍历其余城市各一次，再回到起点，这样便构建了一条连接各个城市的路径。基本蚁群算法中蚂蚁先计算由所在城市转移到其它各个城市的概率，然后按随机比例规则选择具体要访问的城市。

在t 时刻，蚂蚁k 由城市i 转移到另一城市j 的概率为:

式中，tabuk表示蚂蚁k 下一步选择的城市的禁忌表; τi，j为( i，j) 边上的信息素强度; ηi，j为启发式函数，表达式为1/di，j，di，j表示城市i，j 间的距离;α、β 为启发式因子，分别表示信息素与启发式信息对路径选择的重要性。

1.2 信息素更新方式

经过n 个时刻，蚂蚁完成一次循环( i，j) 路径上的信息素更新方式如下:

式中，ρ 为信息素挥发因子，m 为蚂蚁个数，Δτi，j(t+n)为本次循环中路径( i，j) 上的信息素增量，Q 为信息素强度，Lk为蚂蚁k 在本次循环中走过的路径总长度。

2 云模型理论

定义 设X 是一个用精确数值表示的论域，X上对应着定性概念A，对于X 中任意一个元素x，都存在一个有稳定倾向的随机数μA(x) ，叫做x 对A的隶属度，x 在X 上的分布称为云模型，简称为云[8]。

云模型主要由期望值Ex，熵En 和超熵He 三个数值来表征，它们反映了定性概念A 整体上的定量特征。Ex 表示论域空间分布的期望，En 表示定性概念A 的不确定性，超熵He 是熵的不确定性度量。若存在x ～N(Ex，En′2) ，其中En′ ～N(En，He2) ，且满足，则该分布称为正态云模型[9]。图1给出由Ex =0，En =2，He =0.3，随机产生1 000 个云滴的正态云模型示意图。

图1 正态云模型的三个数字特征示意图

3 云自适应蚁群算法(CACA)

3.1 信息素更新方式

本文信息素更新方式采用局部信息素和全局信息素相结合的更新方式。

局部信息素更新是对蚂蚁经过的每一条边上的信息素进行更新，更新方式如下:

其中，0 ＜ξ ＜1，τ0是信息素的初始值。

全局信息素更新不仅是对全局最优路径信息素更新，同时也对确定为次优路径上的信息素进行更新。更新方式如下:

其中，T′为全局最优或次优路径，L( T′) 为相应路径的总长度，μ 为路径对应的最优或次优解在云模型中的隶属度值，全局信息素增量＇则是由隶属度与解的质量共同确定。

3.2 信息素取值区间界定

针对蚁群算法运行过程中易出现停滞及扩散问题，本文将信息素的取值范围限定在区间[τmin，τmax]内，判断公式如下:

在算法寻优过程中，每发现一条至今最优路径Tbest，就更新τmax值，τmax定义为1/ρTbest。相应的信息素下界τmin定义为τmax/a，a 是个参数，其值由实验来确定。

3.3 云参数设置及次优解确定

CACA 中涉及到的云参数有期望值Ex，熵En，超熵He 及隶属度阈值q。Ex 设置为算法在每次迭代中找到的全局最优解Best。En 值根据“3En”规则确定，令Ex +3En 为算法找到的全局最差解Worst，因此En =( Worst －Best) /3。He 由En 和信息素分布状况信息值R 共同确定，He =En/R，其中R 值是由信息素分布状况的评价算法得出( 见3.4)。隶属度阈值q 则是根据信息素分布状况信息值R 进行自适应地调整，将q 设定为q=1 －1/R。

次优解则是依据隶属度μ 和隶属度阈值q 的关系来确定。即在每次迭代之后，根据云模型参数Ex，En 和He 值，计算算法找到的可行解的隶属度μ，然后将μ ＞q 的可行解确定为次优解。

3.4 信息素分布状况评价算法

蚂蚁在完成路径构建之后，需要对各条路径上的信息素分布状况进行评价，以便及时调整算法的运行状态。信息素分布状况的评价算法如下:

For 每个城市节点

计算该城市到其他所有城市路径上的平均信息素值;

再统计大于此平均信息素值的路径边数;

End For

对所有城市的大于其平均信息素值的路径边数进行求平均，其值记为R。

3.5 自适应控制机制

由上分析可知，本文CACA 算法的自适应控制机制主要表现在通过信息素分布状况信息值R，能够对云模型参数He 和隶属度阈值q 进行自适应调整，同时动态确定全局次优解范围。若R 值较小，则表示信息素分布得较集中，这时隶属度阈值q 也会较小，相应的也就会有较多的可行解被认定为次优解。这就使得算法在下一次迭代中选择最优路径的概率降低，从而能够提高算法对未知路径的探索能力。若R 值较大，则表示信息素分布得较均匀，这时隶属度阈值q 也会较大，相应的只有较少的可行解被认定为次优解。这就使得算法在下一次迭代中选择最优路径的概率提高，从而能够提高算法对最优路径的开发能力。

3.6 算法流程

本文CACA 算法的基本流程如下:

Step 1. 初始化参数;

Step 2. 随机选择起点;

Step 3. 对每只蚂蚁构建路径，同时进行局部信息素更新;

Step 4. 评价信息素分布状况;

Step 5. 自适应调整云模型中各参数;

Step 6. 确定全局最优及次优路径;

Step 7. 进行全局信息素更新并限定取值区间;

Step 8. 终止条件不满足则转Step2。

4 仿真实验

表1 问题ulysses22 的结果数据分析对比

表2 问题bays29 的结果数据分析对比

为了验证CACA 算法的有效性，本文从TSPLIB数据集中选取ulysses22 问题和bays29 问题( http: //elib. zib. de/pub/mp-testdata/tsp/tsplib/)，将该算法与最成功的蚁群改进算法ACS[10]和MMAS[11]进行仿真实验对比。实验参数如下:最大迭代次数为1 000，蚂蚁个数为100，α =1，β =2，ρ=0.1，ξ=0.1，a=100，τ0=1/n* Len( n 为城市节点数，Len 为最近邻算法找到的初始路径值)。云模型中相关参数则完全由算法根据其自身运行状况自适应地确定。

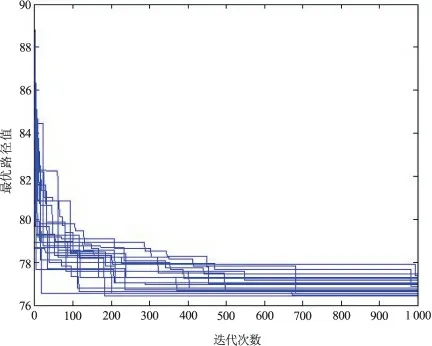
图2 ACS 运行结果(ulysses22 问题)

图3 MMAS 运行结果(ulysses22 问题)

图4 CACA 运行结果(ulysses22 问题)

图5 ACS 运行结果(bays29 问题)

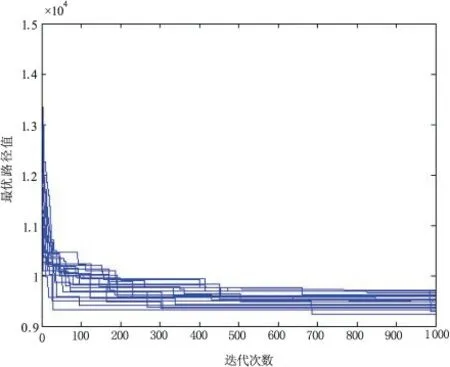
图6 MMAS 运行结果(bays29 问题)

图7 CACA 运行结果(bays29 问题)

使用ACS、MMAS 和CACA 算法，分别对ulysses22 问题和bays29 问题进行20 次独立实验，绘出算法找到的最优路径值随迭代次数的进化曲线图，其中ulysses22 问题的实验结果如图2-图4所示，bays29 问题的实验结果如图5-图7所示。同时，分别对三种算法运行20 次后的结果数据进行统计分析，记录了20 次实验中算法找到的最好值、最差值和平均值，如表1-表2所示。

由图2-图7和表1-表2很容易发现，无论是求解质量还是收敛速度，本文CACA 算法在求解ulysses22 问题和bays29 问题中均明显优于ACS 和MMAS 算法。CACA 算法基本上在迭代100 次左右就可以找到问题的最优解，而且基本上每次实验均可以找到最优解，这说明算法具有优良的全局搜索能力。而ACS 和MMAS 算法在1 000 次迭代后均没有找到问题的最优解。同时，随着问题复杂度(即城市节点数目) 的增加，ACS 和MMAS 算法性能明显下降，而CACA 算法却非常稳定，仍然表现出很好的性能。实验结果也再次表明，通过引入云模型理论及自适应机制，能够使算法具有较好的探索未知解的能力，使其搜索到高质量的解，同时又能使算法充分利用已知解的信息，促进其快速收敛。

5 结束语

本文将云模型作为算法的模糊隶属函数，通过对信息素分布状况进行评价，动态自适应地确定云模型的期望值，熵，超熵以及隶属度阈值，并对确定为全局最优及次优路径进行全局信息素更新，同时将信息素大小限制在一个最大最小区间，以提高算法的求解质量和收敛速度。通过对两个TSP 问题的多次仿真实验，结果表明本文算法具有明显的优越性。今后将进一步完善算法机制，扩大算法的应用领域。

[1]申铉京，刘阳阳，黄永平，等.求解TSP 问题的快速蚁群算法[J].吉林大学学报:工学版，2013，43(1):147-151.

[2]牟廉明. 求解子旅行商问题的改进蚁群算法[J]. 计算机工程，2012，38(23):190-193，197.

[3]刘 振，胡云安.一种多粒度模式蚁群算法及其在路径规划中的应用[J]. 中南大学学报: 自然科学版，2013，44(9):3 714-3 722.

[4]李 擎，张 超，陈 鹏，等.一种基于粒子群参数优化的改进蚁群算法[J]. 控制与决策，2013，28(6):873-878.

[5]刘 全，陈 浩，张永刚，等.一种动态挥发率和启发式修正的蚁群优化算法[J]. 计算机研究与发展，2012，49(3):620-627.

[6]马 颖，田维坚，樊养余.基于云模型的自适应量子粒子群算法[J]. 模式识别与人工智能，2013，26(8):787-793.

[7]刘红庆.基于云模型粒子群算法的WSN 节点部署优化[J]. 华中师范大学学报( 自然科学版)，2013，47(2):186-188.

[8]刘常昱，李德毅，杜 鹢，等.正态云模型的统计分析[J].信息与控制，2005，34(2):236-239，248.

[9]张煜东，吴乐南，王水花，等.基于隶属云模型蚁群算法与LK 搜索的TSP 求解[J]. 计算机工程与应用，2011，47(14):46-55.

[10]Dorigo M，Gambardella L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation，1997，1(1): 53-66.

[11]Stützle T，Hoos H H. MAX-MIN ant system[J]. Future Generation Computer Systems，2000，16(8): 889-914.