矿山边坡爆破振动高程放大效应研究

张伟康 谢永生 吴顺川，3 肖 术

(1.北京科技大学土木与环境工程学院，北京100083;2.中国有色矿业集团有限公司，北京100029;3.金属矿山高效开采与安全教育部重点实验室，北京100083)

针对爆破振动传播过程中的高程放大作用，国内外许多学者采用试验分析、理论分析及数值模拟等手段对其进行了相应研究。唐海［1-2］等的研究表明，地形造成高程放大效应具有一定的方向性，认为竖直方向的放大效应相较于水平方向更为明显;郭学斌［3］等通过一系列爆破振动测试试验实例的分析总结，得到了针对不同类型边坡坡面的高程放大效应公式;谭文辉［4］等利用爆破测试实验数据研究边坡高程影响，得到萨道夫斯基公式中K 与α 会受到传播介质岩性的影响;裴来政［5］认为边坡高程的放大作用，会受到边坡整体的完整性影响;V. Graizer［6］认为造成振动放大效应的主要因素是传播介质中的低速率带和地质地貌特征。

本研究对爆破振动传播过程中涉及到的物理量进行研究，通过量纲分析方法对传统的萨道夫斯基公式进行了改进，推导出了考虑传播介质高程放大效应的振动衰减公式(下文统称为改进公式)。通过与测试试验结果的对比发现，改进公式的推算振速相对误差明显小于传统萨道夫斯基公式，说明改进公式在考虑传播介质高程放大效应时更为准确。

1 工程背景

中色卢安夏穆利亚希北露天铜矿位于赞比亚北部铜带省卢安夏市以西12 km。矿区构造主要为褶皱，基本无断层影响。南帮地层主要为下罗恩群的RL6 组与RL7 组地层，总体呈顺倾趋势，平均倾角约40°，不利于边坡的稳定。其中RL6 组上部为云母片岩，下部为泥岩，RL7 组主要为泥质石英岩，局部夹有云母片岩和砾岩，岩层上部为风化或强风化。

现场地质调查和钻探资料表明:矿区地表岩石基本为软岩，风化严重、易破碎、强度低，风化深度一般不超过80 m，深部岩层为风化不严重的硬岩，强度相对较高。目前南帮固定边坡高度已达120 m，边坡最终高度将达200 m，最终边坡角为38° ～42°。随着开采进度的不断推进，现场爆破作业十分频繁。

2 爆破振动监测试验

2.1 试验方案

现场试验仪器采用爆破振动监测系统，如图1 所示。该系统主要由传感器、振动监测仪和微型计算机等组成。测振仪与计算机配合使用，分析速度快，波形清楚，可在现场通过仪器本身的功能读出特征值，预览采集到的信号波形。

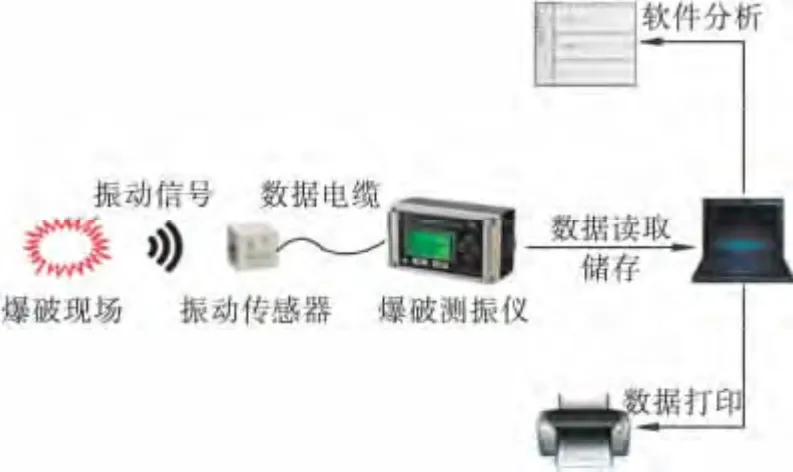
图1 爆破振动监测系统Fig.1 Monitoring system of blasting vibration

在现场试验中，将测振仪由爆心至边坡均匀布设，以测得不同爆心距质点的振动特征。

2.2 试验结果处理

本次爆破测试试验分4 次完成，每次试验布设5个监测点，共布设20 个监测点，获得有效监测数据20 组。4 次试验的监测点分A、B 组沿边坡不同台阶布置，其测试结果如表1 所示。

爆破振动涉及的物理量较多，为分析爆破振速的衰减规律，前苏联的萨道夫斯基等人通过研究集中药包的爆破地震效应，对大量的实测数据进行归纳推算得到经验公式，为国内外工程界普遍应用。其具体形式［7］为

式中，V 为质点振速峰值，cm/s;Q 为炸药量，kg，延时爆破时为最大单段药量，齐发爆破时为总药量;r为爆心距，即监测点到爆破区域的水平距离，m;K、α 为特定区域的场地系数和振动衰减指数。

表1 爆破测试试验结果Table 1 Result of blasting monitoring test

利用传统萨道夫斯基公式对表1 试验结果进行回归分析，分别得到矿区南帮边坡的场地系数K 和振动衰减系数α，进而推算出边坡爆破振速的衰减规律，如表2 所示。

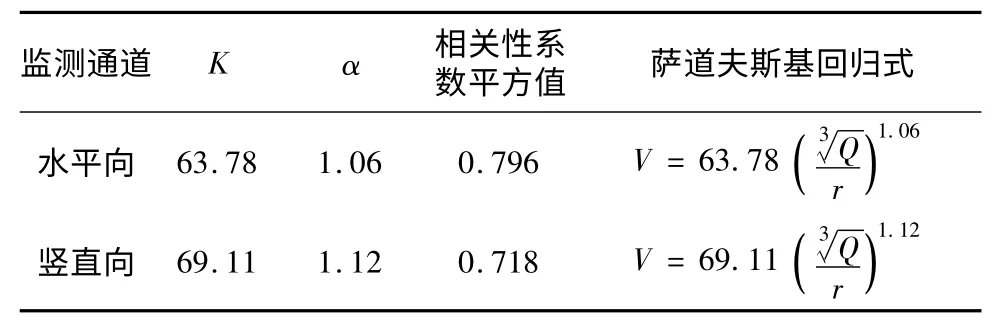
表2 测试试验数据回归结果Table 2 Regression result of monitoring data

3 考虑高程放大效应的振速改进公式

影响爆破振动传播规律的因素比较复杂，而高程放大效应通常受爆破荷载、振动传播介质特性等因素影响［8］。根据以往研究成果表明，爆破振动在传播过程中涉及到的物理量如表3 所示。

表3 影响爆破振动传播规律的物理量［9］Table 3 Physical quantities affecting the propagation rule of blasting vibration

根据白金汉定理［10］(Buckingham theorem)，所有物理量之间的函数关系可以表示为

选取高硫铝土矿试样，参照GB/T 2007.1—1987、GB/T 2007.2—1987制样，过75μm(200目)筛网，并在(110±5)℃烘箱内烘约2h，置于干燥器内，冷却，备用。

由表3 可知，影响爆破振动传播规律的物理量有10个。在一般量纲分析过程中，所取独立量纲个数通常为3，不妨取Q(M)、r(L)、c(LT－1)为独立量纲，则需研究的无量纲量为7 个，以π 代表无量纲量，有

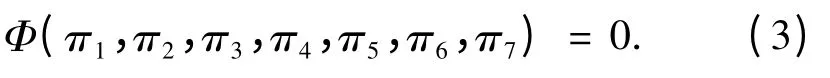
依照表3 中的物理量，令

其中，α、β、γ 为待定系数。

根据量纲齐次原则，因π 为无量纲量，可知H 与Qαrβcγ量纲相同，有

所以可知α=0，β=1，γ=0，所以有

同理有:

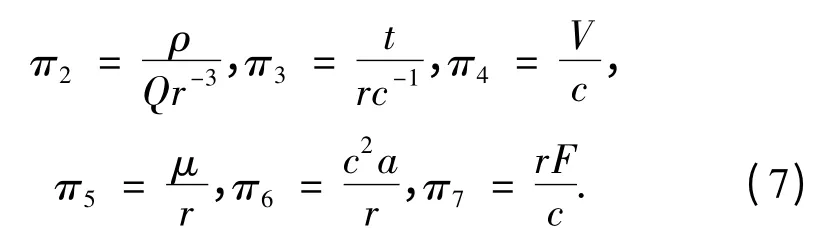
将π1至π7代入式(3)得:

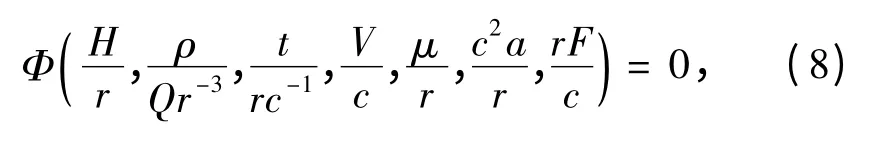
或

由白金汉定理，函数关系的物理量进行乘法、乘方或者取倒数运算，原函数关系仍成立，所以有

对π1、π2进行如下运算，设其结果为π8:

根据传统萨道夫斯基公式的推算方法，当考虑边坡高程放大影响时，不妨将此函数关系写为

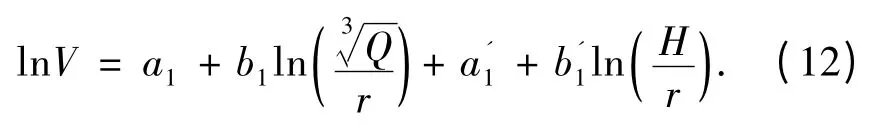
设a1=lnk1，则有

其中，k1代表振动传播地形平整时的场地系数。将上式代入式(12)有

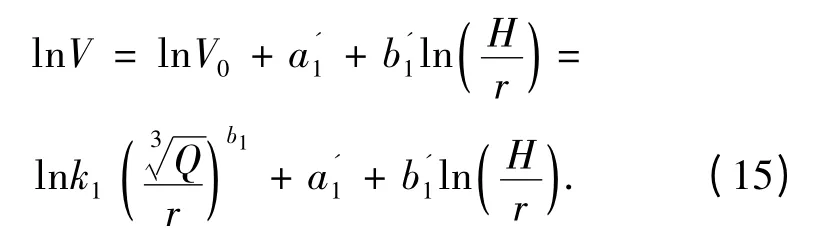
其中，k2为边坡地貌影响系数，b2为高程差影响系数。该公式考虑了传播介质的高程放大效应，可认为是由传统萨道夫斯基公式与改进部分组合而成的。使用过程中，待定系数仍需通过振动测试试验数据进行回归得到。

4 工程验证分析

以表1 中的水平方向振速为例进行研究，将无高程差的测点数据进行回归，得到式(13)中k1=65.41，b1=1.02。将k1与b1代入式(14)，推算出测点对应的平整地形振速V0，与具有高程差的测点实测振速进行对比，如表4 所示。

表4 试验测试结果Table 4 Result of the monitoring test

以表4 中数据作为研究样本，将H/r 作为横轴，Vx/V0作为纵轴进行回归分析，得到k2=0.74，b2=0.26。所以对于露天矿区南帮边坡区域，考虑高程放大效应爆破振速衰减规律形式为

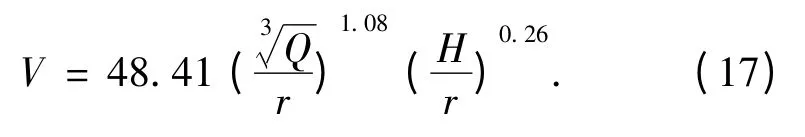
将测点振速的现场试验结果同萨道夫斯基公式和改进公式的推算值进行对比，如表5 所示。

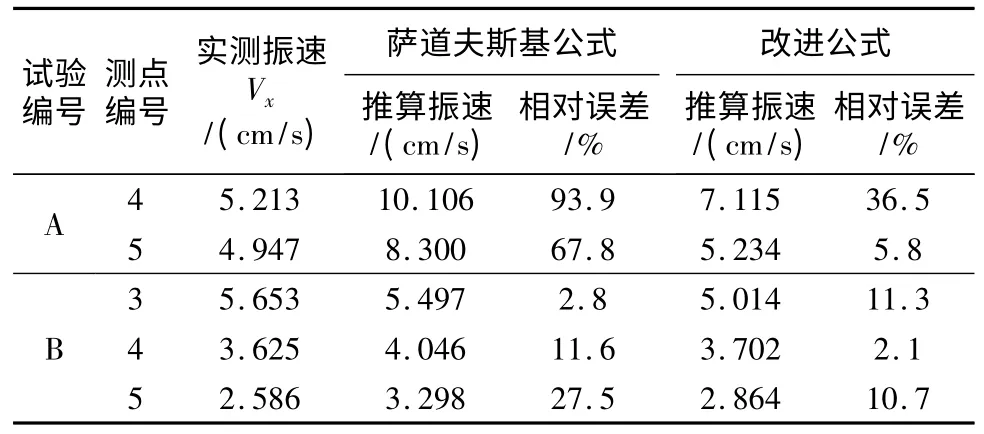
表5 推算振速精度对比Table 5 Comparison of the calculated velocity accuracy

由表5 中数据及图2 可以看出，萨道夫斯基公式与改进公式的平均相对误差分别为:40.7% 与13.3%。A、B 两组试验数据的回归结果表明，对于高程起伏变化较大的振动传播介质，利用萨道夫斯基公式推算的振速误差较大，平均误差为40.7%，最大误差可达93%;利用改进公式得到的推算振速误差较小，平均误差为13.3%，最大误差为36.5%。可以得出，在爆破区域地形高程起伏较大时，改进公式可以较准确地反映爆破振速的衰减规律。另外，对比图3中各组推算误差可以发现，除B3 组之外的其余数据，利用改进公式的推算误差均降至传统萨道夫斯基公式的38%以下，推算精度大为提高;对于B3 组数据，尽管改进公式的误差大于传统公式，但其误差仅为11.3%，属可以接受的误差范围。

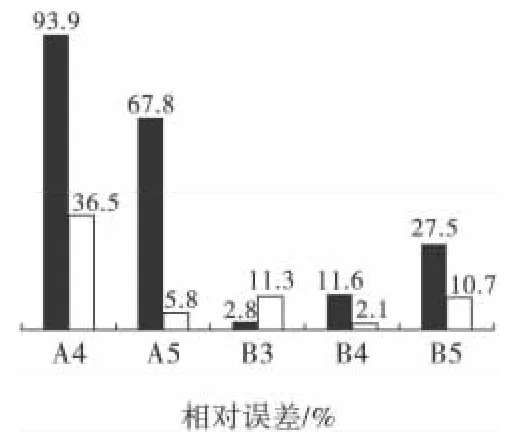
图2 相对误差对比Fig.2 Comparison of the vibration velocity error

5 结 论

(1)分析了可能影响爆破振速衰减规律的物理量，利用量纲分析原理得出了考虑传播介质高程放大效应的爆破振动公式。

(2)以穆利亚希露天矿爆破测试试验为工程实例，通过对比分析得出，当传播介质高程起伏较大时，传统的萨道夫斯基公式在推算爆破振速时误差较大，平均误差可达40.7%，得出的改进公式推算出的振速相对误差较小，平均为13.3%，说明得出的改进公式可以较准确地反映高程对爆破振速的放大效应。

［1］ 唐 海，李海波.反映高程放大效应的爆破振动公式研究［J］.岩土力学，2011，32(3):820-824.

Tang Hai，Li Haibo.Study of blasting vibration formula of reflecting amplification effect on elevation［J］. Rock and Soil Mechanics，2011，32(3):820-824.

［2］ 唐 海，李海波，蒋鹏灿，等. 地形地貌对爆破振动波传播的影响实验研究［J］.岩石力学与工程学报，2007，26(9):1817-1823.

Tang Hai，Li Haibo，Jiang Pengcan，et al.Experimental study on the effect of topography on the propagation of blasting wave［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26(9):1817 –1823.

［3］ 郭学斌，肖正学，张志呈.爆破振动作用的坡面效应［J］.岩石力学与工程学报，2001，20(1):83-87.

Guo Xuebin，Xiao Zhengxue，Zhang Zhicheng. Slope effect of blasting vibration［J］.Chinese Journal of Rock Mechanics and Engineering，2001，20(1):83-87.

［4］ 谭文辉，璩世杰，毛市龙，等. 边坡爆破振动高程效应分析［J］.岩土工程学报，2010，32(4):619-623.

Tan Wenhui，Qu Shijie，Mao Shilong，et al.Altitude effect of blasting vibration in slopes［J］. Chinese Journal of Geotechnical Engineering，2010，32(4):619-623.

［5］ 裴来政.金堆城露天矿高边坡爆破震动监测与分析［J］. 爆破，2006，23(4):82-85.

Pei Laizheng. Monitoring and analysis of blasting vibration at the high slope of Jinduicheng open-pit mine［J］.Blasting，2006，23(4):82-85.

［6］ Graizer V.Low-velocity zone and topography as a source of site amplification effect on Tarzana Hill，California［J］. Soil Dynamics and Earthquake Engineering，2009，29(2):324-332.

［7］ 吕 涛，石永强，黄 诚，等. 非线性回归法求解爆破振动速度衰减公式参数［J］.岩土力学，2007，28(9):1871-1878.

Lu Tao，Shi Yongqiang，Huang Cheng，et al.Study on attenuation parameters of blasting vibration by nonlinear regression analysis［J］.Rock and Soil Mechanics，2007，28(9):1871-1878.

［8］ 石 崇，周家文，任 强，等. 单面边坡高程放大效应的射线理论解［J］.河海大学学报:自然科学版，2008，36(2):238-241.

Shi Chong，Zhou Jiawen，Ren Qiang，et al.Ray theory solution of the elevation amplification effect on a single-free-face slope［J］. Journal of Hehai University:Natural Sciences，2008，36(2):238-241.

［9］ 蒋 楠，周传波，平 雯，等. 岩质边坡爆破振动速度高程效应［J］.中南大学学报:自然科学版，2014，45(1):237-243.

Jiang Nan，Zhou Chuanbo，Ping Wen，et al.Altitude effect of blasting vibration velocity in rock slopes［J］.Journal of Central South University:Science and Technology，2014，45(1):237-243.

［10］ Buckingham E.On physically similar system:illustration of the use of dimensional analysis［J］. Physical Review，1914，4(4):345-376.