灰色预测模型背景值改进方法比较分析

周 清，王奉伟

(1.东华理工大学测绘工程学院，江西南昌 330013;2.江西省数字国土重点实验室，江西南昌 330013)

GM(1，1)模型是灰色系统理论的重要内容，由于建模过程简单，模型表达式简洁，便于求解，能较好地对系统行为特征值进行预测，在很多领域得到了广泛的应用。但是GM(1，1)模型在应用的过程中也出现了预测精度不高的情形，因此对GM(1，1)模型的改进是当前研究的热点，背景值的构造是影响GM(1，1)模型拟合和预测精度的关键因素之一。谭冠军(2000)，姚颖康等(2009)采用了区间面积和重构背景值方法优化传统的GM(1，1)模型;周世健等(2002)，李大军等(2002)采用了背景值最佳生成系数法重构背景值，建立了PGM(1，1)模型;王钟羡等(2003)，李星毅等(2011)，王国兴(2013)，罗党等(2003)，毛文晋等(2011)，胡炎丙等(2013)采用了积分重构背景值方法对传统的GM(1，1)模型进行改进。为进一步探究三种方法的适用性和优劣性，文中通过三个实例进行比较分析。

1 传统的GM(1，1)模型

传统的GM(1，1)的建模原理及过程如下:

设原始数据序列为

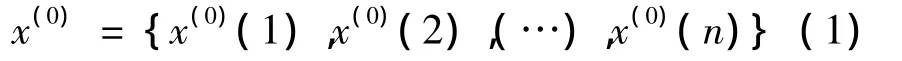
进行一次累加生成得到新的序列

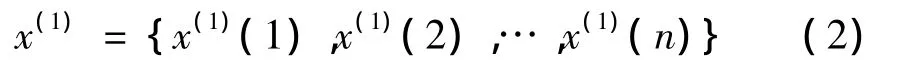
其中α、μ为待定参数，通过最小二乘有

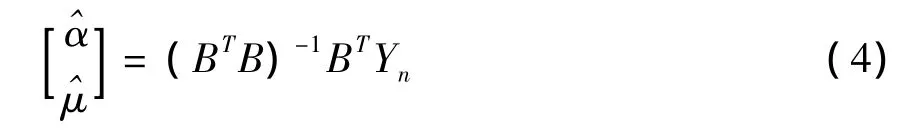
式中

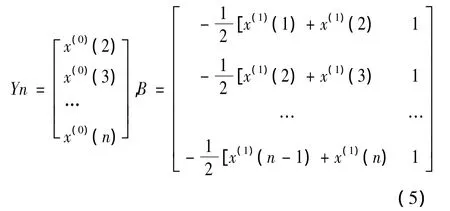
解方程(3)得:

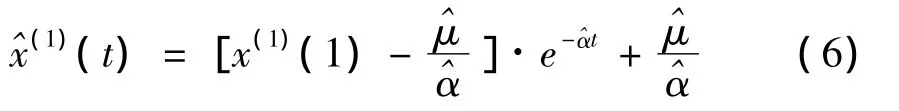
GM(1，1)模型的时间响应序列为

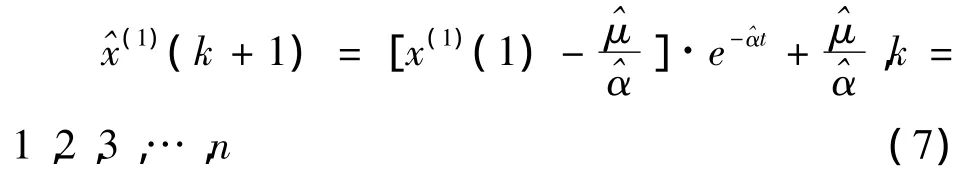
还原到原始数据可得原始序列的灰色预测模型为

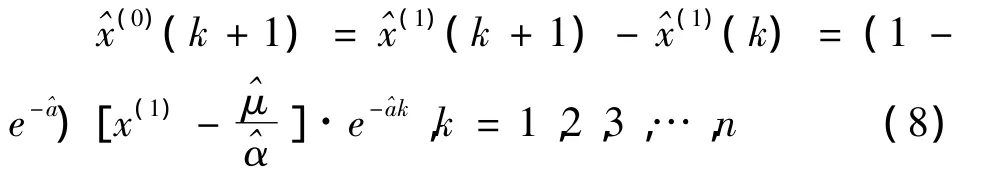
2 背景值的改进

2.1 区间面积和重构背景值

谭冠军(2000)，姚颖康(2009)认为传统的GM(1，1)模型在求解待定参数α，μ时，通过梯形面积代替曲边梯形面积，造成模型预测精度的降低。传统模型的背景值为

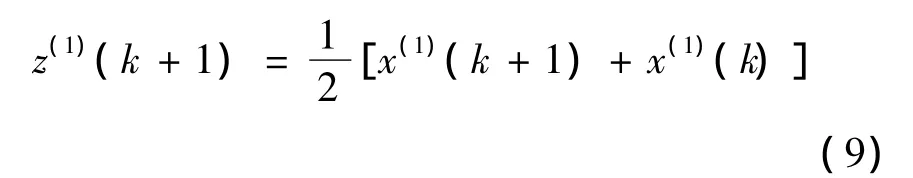
背景值的构造用曲边梯形面积更合适，但是原始序列是离散数据点，同时x(1)(t)未知，因此考虑将区间［k，k+1］等分为n个小区间，用n个小区间的面积和构造背景值。

重构的背景值为

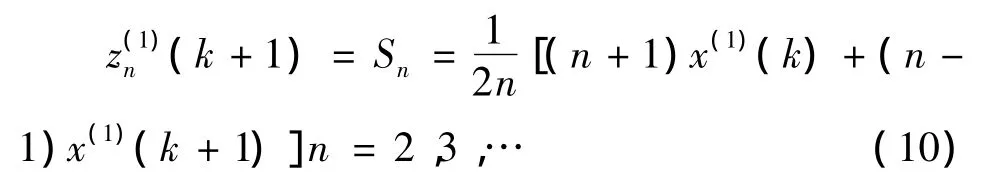
2.2 背景值最佳生成系数法重构背景值

传统的GM(1，1)模型在定义背景值时认为在Δt=1的很短时间内，x(t)→x(t+Δt)之间不会发生突变，因此取它们的平均值为背景值，但是在实际应用过程中也不可避免的会出现突变的情况，故而提出了一种新的背景值构造方法，构建PGM(1，1)模型，如(11)式(周世健，2002;李大军，2002)。式中p为背景值最佳生成系数。

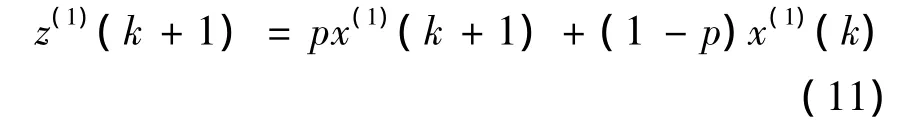
2.3 积分法构建背景值

王钟羡等(2003)，李星毅等(2011)，王国兴(2013)，罗党等(2003)，毛文晋等(2011)，胡炎丙等(2013)同样认为背景值的构造用曲边梯形面积更加合理，因此采用积分法重构背景值如(12)式。

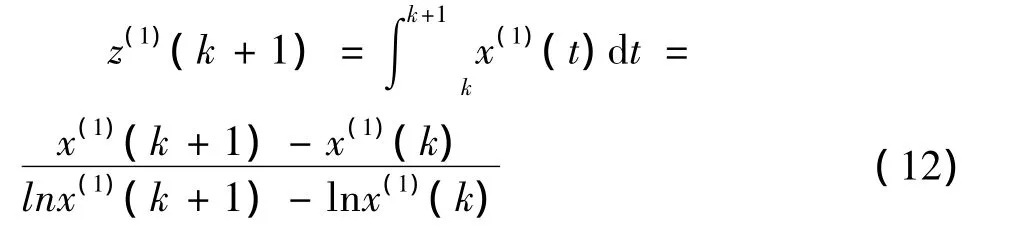
3 实例分析

实例1:以x=e0.8(i－1)，i=1，2，…，7生成原始数据，x(0)={1.000，2.226，4.953，11.023，24.533，54.598，121.510}。用传统的GM(1，1)模型，区间面积和、背景值最佳生成系数、积分四种重构背景值方法对模型进行拟合和预测。为了便于比较分析，采用MAE和MAPE为评价指标。其中，MAE= (∑e)/n，MAPE=(∑(e/y))/n，e为残差值，n数据个数。具体结果见表1、表2。

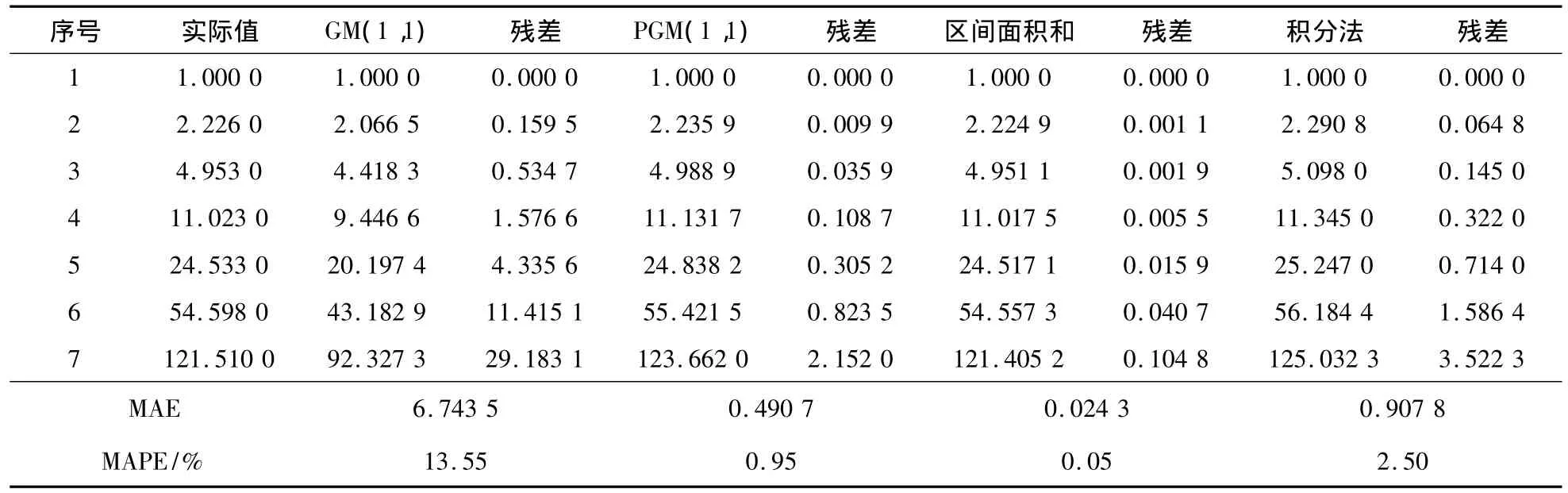
表1 各模型拟合情况对比(实例1)Table 1 Simulated Values for Four Models(Example 1)

表2 各模型预测结果与实际值对比(实例1)Table 2 Comparison of the results with Predicted Values of the Four Models(Example 1)

从实例1的拟合和预测精度可以看出，对于呈近似指数增长的序列，三种方法均优于传统的GM (1，1)模型，但是区间面积和重构背景值方法改进效果更为明显。

实例2:原始数列 ={2.718，7.389，20.086，54.598，148.41，403.43，1096.61}(王国兴，2013)。由于数据增长急剧，这是一个高增长序列。采用前五组数据建模并预测后两组数据，结果见表3、表4。

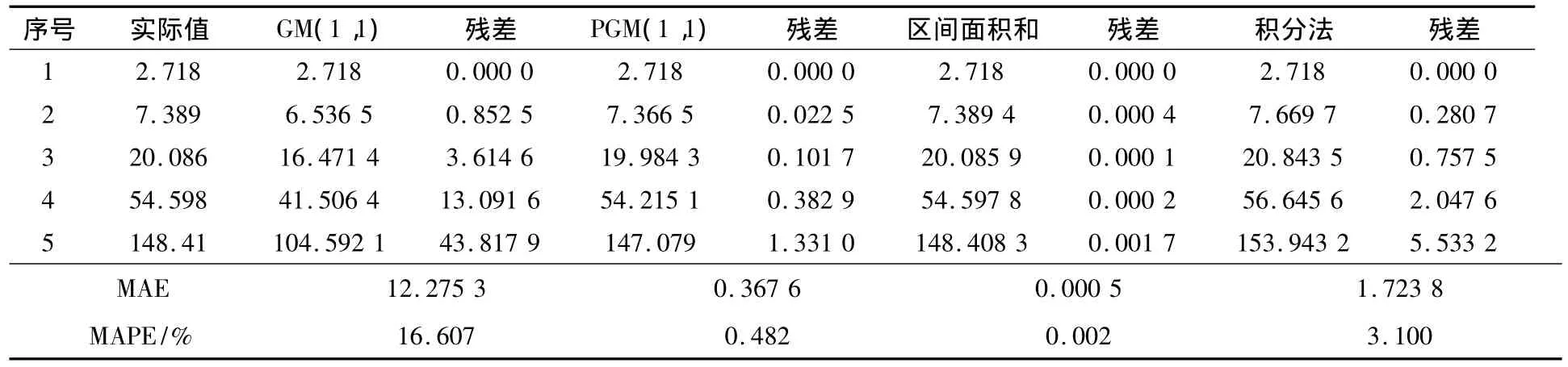
表3 各模型拟合情况对比(实例2)Table 3 Simulated Values for Four Models(Example 2)

表4 各模型预测结果与实际值对比(实例2)Table 4 Comparison of the results with Predicted Values of the Four Models(Example 2)

由表3和表4发现，对于高增长的序列，三种方法的拟合和预测精度均高于传统的GM(1，1)模型，区间面积和重构背景值方法改进效果尤为明显。

实例3:利用黄声享等(2003)中某炼钢厂钢炉的沉降观测点的10期沉降观测数据，={2.79，4.34，5.17，6.97，7.63，8.4，9.13，9.74，10.09，10.46}。由于数据变化平缓，为低增长数列。采用前七组数据建模并预测后三组数据，结果见表5、表6。

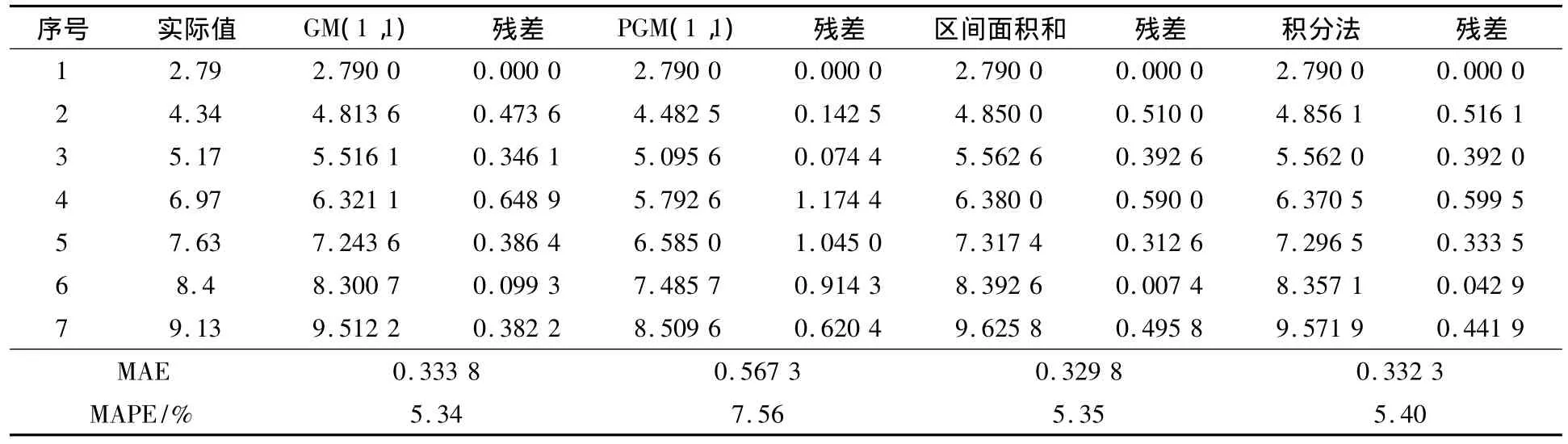
表5 各模型拟合情况对比(实例3)Table 5 Simulated Values for Four Models(Example 3)

表6 各模型预测结果与实际值对比(实例3)Table 6 Comparison of the results with Predicted Values of the Four Models(Example 3)

从实例3的拟合和预测精度可以看出，对于低增长的序列，三种方法与传统的GM(1，1)模型在拟合精度上相当，但在预测精度上背景值最佳生成系数法构建的PGM(1，1)模型更高，其他两种方法和传统的GM(1，1)模型相当。

4 结论

通过实例分析发现，对于呈近似指数增长的序列及高增长序列，应用区间面积和重构背景值方法改进GM(1，1)模型，在拟合和预测精度上较传统的GM(1，1)模型、积分重构背景值改进GM(1，1)模型、PGM(1，1)模型更好。对于低增长序列，三种方法和传统的GM(1，1)模型拟合精度相当，但是在预测精度上PGM(1，1)模型更好。

胡炎丙，陈勇明，赵月.2013.迭代优化背景值的GM(1，1)模型改进［J］.统计与决策，393(21):34-36.

黄声享，刘经南，柳响林.2003.小波分析在高层建筑动态监测中的应用［J］.测绘学报，32(2):153-157.

李大军，孙旭红，汤拥军.2002.PGM(1，1)灰色预测模型及其应用［J］.华东地质学院学报，25(1):40-43.

李星毅，李奎，施化吉，等.2011.背景值优化的GM(1，1)预测模型及应用［J］.电子科技大学学报，40(6):911-914.

罗党，刘思峰，党耀国.2003.灰色模型GM(1，1)优化［J］.中国工程科学，5(8):50-53.

毛文晋，冉璐.2011.基于改进背景值算法的优化GM(1，1)模型及其应用［J］.统计与决策，336(12):29-31.

谭冠军.2000.GM(1，1)模型的背景值构造方法和应用(Ⅰ)［J］.系统工程理论与实践，21(4):98-103.

王国兴.2013.GM(1，1)模型的改进及应用［J］.应用泛函分析学报，15(3):211-217.

王钟羡，吴春笃.2003.GM(1，1)改进模型及其应用［J］.数学的实践与认识，33(9):20-25.

姚颖康，张春艳，张坤.2009.改进的GM(1，1)模型在滑坡变形预测中的应用［J］.水文地质工程地质，36(5):102-106.

周世健，赖志坤，藏德彦，等.2002.加权灰色预测模型及其计算实现［J］.武汉大学学报:信息科学版，27(5):451-455.