基于二次场算法的CSEM二维有限单元法正演

殷哲琦，张志勇，黄临平，蓝泽鸾，周 乾

(东华理工大学核工程与地球物理学院，江西南昌 330013)

自Coggon(1971)将有限单元法引入地球物理领域起，有限单元法在地球物理电磁场计算问题中得到了广泛应用;陈乐寿(1981)提出了以矩形单元为主结合使用部分三角形单元对有限单元法进行改进，提高了对分界面形状的适应能力;Wannamaker等(1986)利用有限单元法对带地形的二维大地电磁(MT)进行数值模拟;Bouchard(1988)对大地电磁进行了二维地形改正的研究，表明起伏地形会产生明显的假异常，说明在进行MT数据解释时应消除地形的影响;Key等(2006)人利用非结构化自适应有限元网格对二维大地电磁进行研究，研究表明非结构化和自适应算法可以很好地对复杂2D模型进行剖分，自适应算法采用的是一种后验误差估计，其目的是使网格剖分能更好的满足实际模型，通过不断迭代得到最佳网格剖分，减少计算误差从而提高计算精度。国内学者也对有限元算法进行了研究;徐世浙等(1995)利用有限单元法对电导率连续分层变化的层状介质的大地电磁进行了正演研究;为提高计算精度，史明娟等(1997)对基于二次插值四边形网格剖分进行了大地电磁正演研究;柳建新等(2009)采用自适应有限元算法，通过非结构化自动网格剖分技术，使得网格剖分较好拟合复杂地形的边界;由于有限单元法进行数值模拟的网格边界为截断边界，影响计算精度，张继锋等(2010)模拟了MT的截断边界对计算结果的影响。

本文利用二次场进行CSEM数值模拟，在非均匀介质地电结构中传播电磁总场可以分为背景场和二次场的总和，研究工作从麦克斯韦方程组出发，导出了同时考虑电阻率与磁导率异常的可控源电磁法二次场方程;采用了基于二叉树结构的三角单元剖分，该剖分方法网格生成速度快、节点编号与访问容易，具有较好的拟合地质单元与地形的效果;并推导了三角单元双线性与双二次插值的单元钢度矩阵表达式;分别对电阻率异常及磁导率异常模型进行了试算，结果表明二次场算法无需对场源区域进行剖分，可有效的减小计算区间，提高计算效率;另二次场算法边界处理简单，有利用提高计算精度，解决了低频计算不稳定问题。

1 基于二次场的有限单元法二维大地电磁场数值模拟原理

考虑地下电导率与磁导率变化，则二次电磁场满足下面形式的麦克斯韦方程组(刘小军，2007):

其中取场值负谐变(e－iωt)，ω为角频率;Eb、Hb为一次电场与磁场，Es，Hs为二次电场与磁场=σiωε为复电导率，σ为电导率，σ=Δσ+σ0，其中Δσ为异常电导率、σ0背景电导率，ε为介电常数(取真空中介电常数ε0=8.8542×10－12F·m－1); μ磁导率、Δμ为异常磁导率，其中=iωμ= iωΔμ(取真空中磁导率μ0=4π×10－7H·m－1)。

二维条件下，取地质体走向为y轴，场源为沿y轴向无限延伸的线电流源，则走向方向二次电场满足偏微分方程(刘云，2010)，

式(2)为线源二维可控源二次场方程。

如视(2)式右端项为“源项”，则可写成以下形式，

构造(3)式的泛函

微分方程(3)的解与求解泛函(4)的极值问题等价。

对研究区域剖分，泛函式(4)可表示为离散形式(马为，2008)

对(5)变分式，得到有限单元计算方程组

求解上式即可得到节点的场值。

2 网格剖分

鉴于各种地表的地球物理观测方法，一般观测数据对浅部分辨率高、向深部逐渐降低，基于这样的认识，设计了基于二叉树的收缩网格剖分算法(Li，2008)。算法原理，假设由模型底部向地表分辨率变高，采用四边形剖分，则其具有二叉树式的结构;剖分形成的四边形可进一步三角化，实现三角剖分;利用对三角单元边的访问可实现二次插值;当然有二次插值结点的三角形还可进一步离散为四个三角形实现二次剖分，典型的剖分如图1 (张志勇，2013)。

3 钢度矩阵计算

收缩网格剖分的最后单元为一次和二次插值三角形，利用自然坐标可推导得单元上的钢度矩阵(Liu，1990)。三角单元节点逆时针编号i，j，m，如果有二次插值节点则为i，j，m，r，p，q，其中r为边i，j中点、p为边j，m中点、q为边m，i中点。如图2所示，下文中a，b，c的定义来自徐世浙(1994)。

3.1 泛函式第一项单元积分

当选择双线性插值，K1e矩阵元素为

当选择双二次插值，K1e矩阵元素为

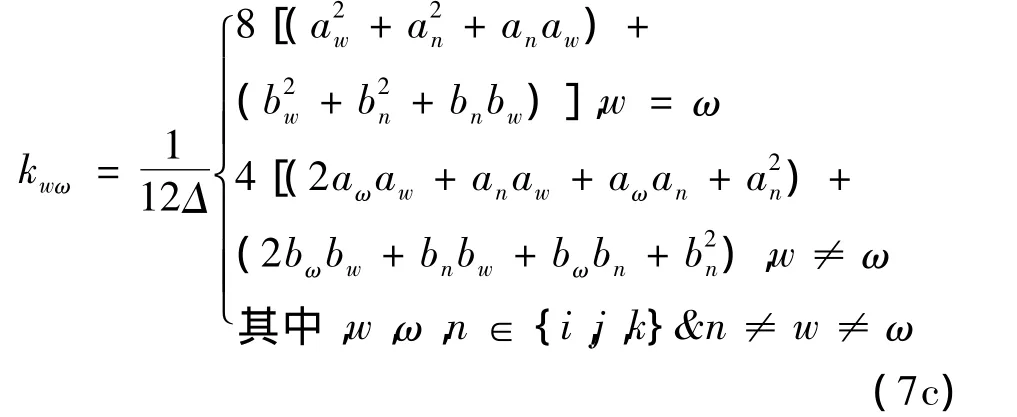
图1 基于二叉树的剖分结构Fig.1 The split structure based on the binary tree

图2 三角单元结构Fig.2 Triangle unit structure

3.2 泛函式(4)第二项单元积分

当选择双线性插值，则有

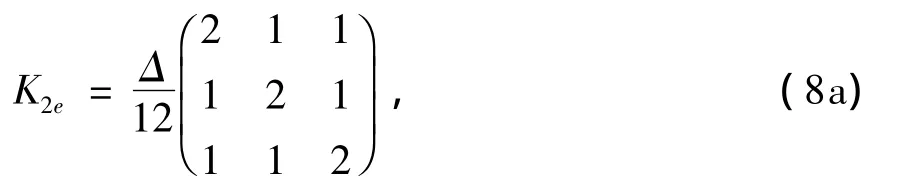
当选择双二次插值，则有

式(7)～(8)中Δ为三角形单元的面积。

3.3 泛函式源项计算

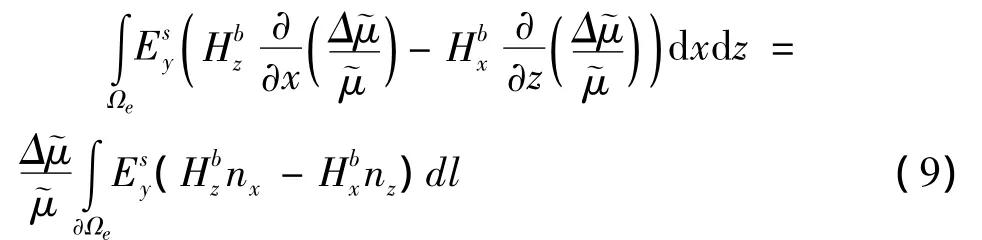
nz表示外法线方向与z轴夹角余弦。

当选择双线性插值，K5e三角单元闭合曲面积分，其中边上的积分矩阵元素为

当选择双二次插值

其中l为计算边的长度。

将K5e中nx换为nz即可得到K6e。

4 算例分析

在均匀半空间内设置三个截面为长方形(宽400 m，高500 m)的二度体，二度体上顶埋深100 m，间距1 600 m，模型设置如图3。在地表采用进行可控源电磁测量，观测频率为(1～214 Hz)。

图3 计算模型Fig.3 Model of test

算例一:电阻率模型，取异常体磁导率、介电常数等于围岩，围岩电阻率ρ0=100 Ω·m，M1异常体ρ1=50 Ω·m，M2异常体ρ2=100 Ω·m，M3异常体ρ3=200 Ω·m。

计算结果如图4，在只考虑电阻率影响条件下，M1形成低阻圈闭异常，最低电阻率等值线70 Ω·m;M3形成高阻圈闭异常，最高电阻率等值线130 Ω·m;过渡带与近区数据计算稳定。

图4 算例一计算结果Fig.4 Contours of apparent resistivity and phase for first test

算例二:磁导率与电阻率模型，取异常体介电常数等于围岩，围岩电阻率ρ0=100 Ω·m，磁导率为μ0，M1异常体ρ1=50 Ω·m，μ1=2μ0，M2异常体ρ2=100 Ω·m，μ2=2μ0，M3异常体ρ3=200 Ω ·m，μ3=2μ0。

计算结果如图5，同时考虑电阻率、磁导率影响条件下，三个异常体均形成明显异常。M1形成低阻圈闭异常，最低电阻率等值线80 Ω·m;M2形成高阻圈闭异常，最高电阻率等值线120 Ω·m;M3形成高阻圈闭异常，最高电阻率等值线130 Ω·m;过渡带与近区数据计算稳定。磁导率对视电阻率明显的影响，使视电阻率增大。

5 结论

本文引入二次场算法实现了二维CSEM正演模拟。研究了同时考虑电阻率与磁导率的可控源电磁法二次场方程，采用基于二叉树结构的收缩网格剖分，推导了三角单元双线性与双二次插值单元钢度矩阵，实现了有限单元模拟。实践表明，二次场算法无需对场源区域剖分，可有效的减小剖分区间，提高计算效率;与总场算法相比边界处理简单;解决可控源低频计算不稳定问题、提高了计算精度。对电阻率异常模型及同时考虑电阻率与磁导率异常的试算，试算表明磁导率对可控源视电阻率产生明显影响，使电阻率变大。

图5 算例二计算结果Fig.5 Contours of apparent resistivity and phase for second test

陈乐寿.1981.有限元法在大地电磁场正演计算中的应用及改进［J］.地球科学，(2):241-260.

陈小斌，张翔，胡文宝.2000.有限元直接迭代算法在MT二维正演计算中的应用［J］.石油地球物理勘探，35(4):487-496.

柳建新，蒋鹏飞，童孝忠，等.2009.不完全 LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用［J］.中南大学学报(自然科学版)，40(2):484-491.

刘小军，王家林，于鹏.2007.基于二次场的二维大地电磁有限元法数值模拟［J］.同济大学学报(自然科学版)，35(08):1113-1117.

刘云，王绪本.2010.大地电磁二维自适应地形有限元正演模拟［J］.地震地质，32(03):382-391.

马为，陈小斌，赵国泽.2008.大地电磁测深二维正演中辅助场的新算法［J］.地震地质，30(02):525-533.

史明娟，徐世浙，刘斌.1997.大地电磁二次函数插值的有限元法正演模拟［J］.地球物理学报，40(3):421-430.

徐世浙.1994.地球物理中的有限单元法［M］.北京:科学出版社: 229-247.

徐世浙，于涛，李予国，等.1995.电导率分块连续变化的二维MT有限元模拟(Ⅰ)［J］.高校地质学报，1(2):65-73.

张继锋，汤井田，王烨，等.2010.基于预处理共轭梯度的大地电磁快速正演［J］.中南大学学报:自然科学版，41(5):1877-1882.

张志勇，刘庆成.2013.基于收缩二叉树结构网格剖分的大地电磁二维有限单元法正演研究.石油地球物理勘探，48(3):482-487.

Bouchard M C A K.1988.Two-dimensional terrain correction in magnetotelluric surveys［J］.Geophysics，53(6):854-862.

Coggon J.H.1971.Electromagnetic and electrical modeling by the finite element method［J］.Geophysics，36(1):132-135.

Davis T.A.2006.Direct methods for sparse linear systems［M］.SIAM，99-133.

Key K，Weiss C.2006.Adaptive finite-element modeling using unstructured grids:The 2D magnetotelluric example［J］.Geophysics，71 (6):G291-G299.

Li Y，Pek J.2008.Adaptive finite element modelling of two-dimensional magnetotelluric fields in general anisotropic media［J］.Geophysical Journal International，175:942-954.

Liu J.1990.The Role of Elimination Trees in Sparse Factorization［J］.SIAM Journal on Matrix Analysis and Applications，11(1):134-172.

Wannamaker P.E，Stodt J.A，Rijo L.1986.Two-dimensional topographic responses in magnetotelluric modeled using finite elements［J］.Geophysics，51(11):2131-2144.

Wannamaker P E，Stodt J A，Rijo L.1987.A stable finite element solution for two-dimensional magnetotelluric modelling［J］.Geophysical Journal Research，88(01):277-296.