基于弹性形变的拉索索力测量系统*

蓝章礼，兰天凤，鲁云平

(重庆交通大学 信息科学与工程学院，重庆400074)

0 引 言

拉索作为稳定或承载刚结构件的核心部件，承担了刚结构件的大部分荷载，其健康状况直接影响结构件的内力分布、架构线型和整体安全。拉索作为一种承受拉力的结构构件，广泛应用于桥梁工程中，由于准确测量拉索的索力状态是衡量大桥是否处于正常运营状态的一个重要手段，且拉索索力监测为桥梁的安全与健康的准确分析提供重要依据，因此，对桥梁的拉索索力进行监测意义重大［1～4］。

桥梁拉索索力的测量是工程界的一个难题，对索力的在线监测是在国内外桥梁领域受到广泛重视的一项研究课题［5～8］。当前比较常用的方法有千斤顶压力表测定法、压力传感器法、频率测定法、磁通量法［9～12］。在目前的这些测量方法中，千斤顶压力表测定法简单易行，张力范围可调，但结果常存在人为的随机误差，也不适用于成桥的长期在线测量;压力传感器法测量精度最高可达0.5%～1%，但是压力传感器的售价昂贵，自身重量大，只能在特定场合使用;频率测定法应用方便，结果合理，但对于短索有时将过高估计实际索力超过50%;磁通量法测量成本低，又不容易破坏，但该技术在国内应用较少。

本文阐述了基于弹性形变的拉索索力测量系统的原理和实验流程，通过分析试验数据得出拉索形变量与拉索索力值的线性关系，并进行有效验证。

1 测量装置与原理

1.1 测量装置

图1 为所设计的测量装置图［13］。参照拉索一端利用连接装置与待测拉索固定连接，在参照拉索另一端前方的待测拉索上设置支架，支架与参照拉索相邻一端端面留有伸缩缝。位移计通过位移计信号线与位移计读数设备相连，并进而与计算机设备相连。在位移计附近安装相同规格的不受牵引的参照位移计，参照位移计仅仅一端与参照拉杆固定，且其信号线与计算机设备相连。

1.2 系统原理

胡克定律指出:在材料的弹性限度范围内，物体的形变量与引起形变的外力呈正比，其表达式为

图1 测量装置图Fig 1 Diagram of measuring device

或表示为

式中 K 为物体的弹性系数，其大小由材料的性质所决定，F 为物体所受的外力，ΔX 为物体所产生的形变量(弹性形变)。由此可知，只要获得拉索产生的形变量ΔX，即可根据公式计算出索力大小。

基于以上设计的装置和胡克定律，提出下面的测量系统方案:将待测拉索上被两支架固定的一段长度标记为A端和B 端(A 端和B 端之间的长度为定值，设为L0)，如图1所示。在对待测拉索拉伸或压缩前，先用传感器测量B 端参照拉索与支架间的初始间隙，并记录该读数;拉伸或压缩待测拉索后，再次测量伸缩缝的间隙大小，计算两次测量值的差值，即为拉索的形变量，记为ΔL0，用该差值乘以待测拉索受力段距离(即为拉索的总长度L)与待测拉索被测量段距离(A，B 两端之间的距离L0)的比值便可得到待测拉索总形变量

式中 ΔL 为整个拉索的形变量。再根据胡克定律将待测拉索总形变量乘以待测拉索倔强系数即可得到待测拉索所受拉力大小

其中，待测拉索的倔强系数可通过查表或是实验室标定获得。

2 测量过程与方法

2.1 标 定

由系统原理可知，要计算索力值，首先要已知拉索形变量和倔强系数，形变量可以在试验过程中通过位移传感器或更精密的尺度测量工具直接获取，而拉索的倔强系数要通过严格的实验标定，建立游标卡尺读数与拉索张拉力之间的对应关系。标定流程如下:

1)选取和实际测量拉索相同材料(包括直径和长短)的某段钢索作为被测对象;

2)选用液压万能试验机(量程为20 kN)作为拉力试验中的外力提供设备，并固定测量装置;

3)对钢索施加的固定外力，每加载一级等待系统稳定后记录传感器的测量数据;

4)重复步骤(3)4 ～5 次;

5)由以上测量数据计算出拉索的倔强系数K。

2.2 测量步骤

1)对实际拉索固定测量装置并连接位移传感器和信号线，开启无线收发设备，确保远程监测点正常接收数据;

2)由位移传感器测量拉索形变，每间隔1 min 记录一次数据;

3)根据公式(4)计算实际拉索索力。

3 数据处理与分析

3.1 滤 波

由监测系统获得的测量信号，由于测量误差的存在和采集、传输过程中存在各种噪声和干扰，会出现异常或偏离值较大的数据。为提高监测系统的精度，必须对监测所得到的数据进行适当处理以剔除或减小干扰。对于桥梁监测系统获得的监测数据，数据的滤波是常用的简单实用的处理方法。

常见的滤波算法主要有以下几种:限幅滤波算法、中位值滤波算法、算术平均滤波算法、递推平均滤波算法、消抖滤波算法等。考虑桥梁拉索索力的变化缓慢的特点，利用上述各滤波算法的优点，采用限幅消抖滤波算法，该算法结合继承了限幅和消抖的优点，又改进了消抖滤波法中的某些缺陷，避免将新的干扰导入系统。

3.2 数据分析

常有的数据分析方法主要有:简单的数学运算、统计、快速傅里叶变换、基线和峰值分析等。针对本系统研究的特点和目的，只对滤波后的数据进行了时域和频域分析。在时域中，通过观察拉索索力强度随时间的变化情况，得出索力值的总体变化趋势。但是时域分析只能反映信号的幅值随时间的变化，除单频率分量的简谐波外，很难明确揭示信号的频率组成和各频率分量的大小，所以，可通过快速傅里叶变换(FFT)将信号转换到频域，信号的频谱可以提供更直观、丰富的信息。

4 试验验证

4.1 标定实验

按照标定的流程，设计实施了标定实验。选取5 个固定拉力值(1，5，10，15，20 kN)对标定拉索进行加载试验，标定结果如表1 所示。由标定实验可得到拉力F 和拉索的形变量ΔL 间的对应关系。

由表1 可知，测量结果中“位移计读数”的值都是0.02的倍数，这是由于本次测量使用的位移传感器精度是0.02 mm，如果采用精度更高的测量工具，其结果更为理想。

表1 标定数据Tab 1 Calibration datas

根据表1 中的标定数据，将拉索索力值和拉索的形变量进行拟合，拟合结果如图2 所示。

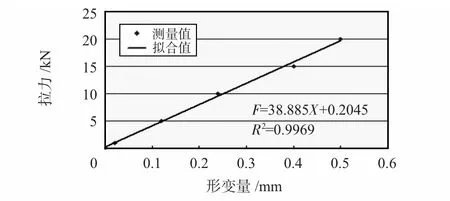
图2 数据拟合关系曲线Fig 2 Curve of data fitting relationship

由图2 可以看出:测量数据在拟合直线两侧均匀分布，有较好的回归性，如图显示拉索索力与拉索形变量间的拟合方程为

拟合的相关系数R2＞0.99，可见拉力F 和拉索的形变量ΔL 之间有很好的线性关系。

4.2 拉力试验验证

对拉索加载固定拉力以验证标定的结果的准确度，验证结果如表2 所示。

由表2 可知，计算拉力值与实际测量值差异不大，当对拉索加载拉力较小时，通过拟合方程F=38.885 X+0.2045计算得到的索力值与实际测量值有偏差，其相对误差约5%，当加载拉力较大时，此偏差逐渐较小，相对误差约2%。

从表2 中相对误差数据可以看到，随着拉索承载拉力的增大，其测量的相对误差整体趋势是逐渐减小。但是当荷载加载为20 kN 时，其相对误差出现跃升之势，误差比较前面的有点偏大，造成这种结果的原因可能是:

1)随着试验中对拉力试验机提供拉力的逐渐增大，试验机表盘的指针并不能标准指到刻度处，其实际提供的拉力要小于19 kN;

2)试验所用的参考拉索是固定长度为0.5 m 的钢索，其长度相对较短导致受力时形变量较小，要减少这样的误差只要增加拉索长度即可。

5 结 论

根据系统测量原理，设计了相应的测量装置，并搭建试验平台，标定拉索倔强系数，利用拉力试验机进行大量的拉力验证试验，通过对数据的分析可以得到以下结论:

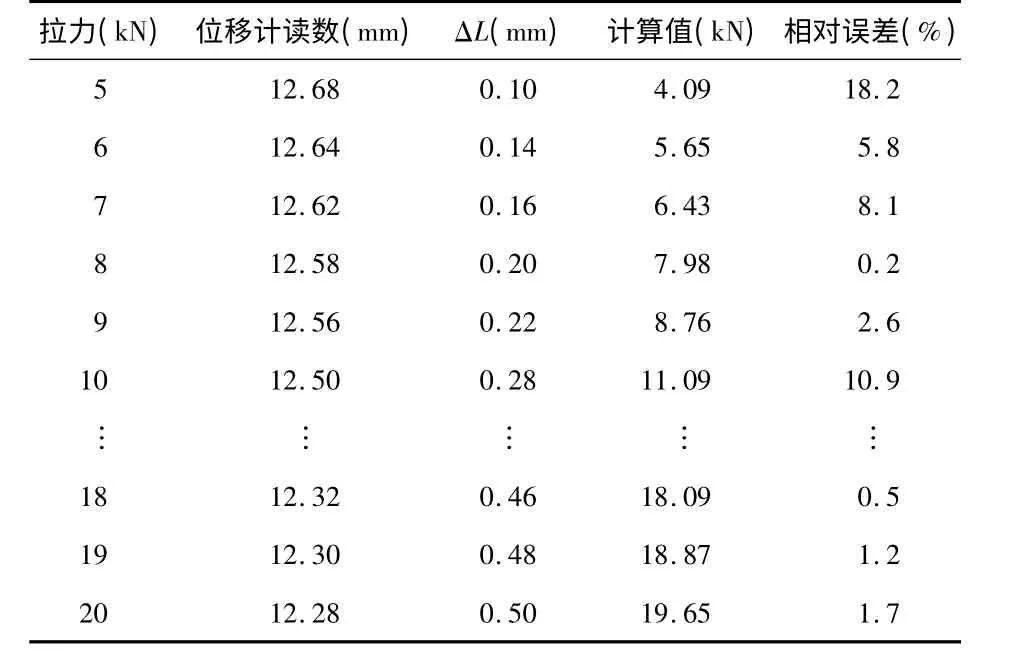
表2 验证结果Tab 2 Proof result

1)拉索索力F 和拉索的形变量ΔL 的存在较好的线性关系;

2)拉索受到的拉力越大，其相对误差越小;

3)基于弹性形变的拉索索力测量装置和方法是可行的。

［1］ Cunha A，Caetano E，Delgado R.Dynamic tests on large cablestayed bridge［J］.Journal of Bridge Engineering，2001，6(1):54－62.

［2］ Sumitro S，Okada Y，Saitoh K.Long－gage optical fiber sensors monitoring on deteriorated structure deformational properties［C］∥Proc of First International Conference on Structural Health Monitoring and Intelligent Infrastructure，Tokyo，2003:1277－1285.

［3］ Ren Weixin，Peng Xuelin，Lin Youqin.Experimental and analytical studies on dynamic characteristics of a large span cable－stayed bridge［J］.Engineering Structures，2005(27):535－548.

［4］ He Youquan.The application research of computer vision in bridge health monitoring［J］.Journal of Communication and Computer，2010，7(2):6－8.

［5］ 荣 立.浅谈钢丝绳无损检测技术［J］.中国科技信息，2005(21):100.

［6］ Zhou Qian，Tao Dexin，Jin Chaoqiu.Analysis on signal feature of magnetism leaking of wires broken in a steel wire rope［J］.Port Operation，2004(2):6－8.

［7］ 姜建山，唐德东，周建庭.桥梁索力测量方法与发展趋势［J］.重庆交通大学学报:自然科学版，2008，27(3):379－382.

［8］ Su Dagen.Analysis of corrosion and failure of bridge diagonal tie rods［J］.Materiais Protextion，1997，30(12):24－26.

［9］ 郭良友，林一宁，李文波，等.武汉长江二桥的索力、温度和应力测量［J］.桥梁建设，1995(3):44－46.

［10］李红杰，苗顺占，傅华明.基于振弦式传感器的桥梁检测系统设计［J］.传感器与微系统，2011，30(6):93－95.

［11］吴康雄，刘克明，杨金喜.基于频率法的索力测量系统［J］.中国公路学报，2006，19(2):62－66.

［12］褚建新，顾 伟.钢丝绳缺陷漏磁场的磁通门检测法［J］.仪器仪表学报，1997，18(4):437－440.

［13］曹建秋，蓝章礼，周建庭.一种大型建筑物拉杆拉力测量装置:中国，ZL201010042020［P］.2010—01—07.