由椭球到圆球的磁传感器补偿技术

范欣林

(北京中航智科技有限公司，北京100167)

0 引 言

低成本电子罗盘以其价格低廉、精度适中、使用简便等特点，越来越多地应用到了人体姿态定位、小型无人机导航、无人驾驶汽车以及康复医疗等领域［1］。

电子罗盘在倾角较大的情况下，航向误差会急剧增大。磁传感器传统的补偿方法主要以零位和灵敏度的调整为主，难以从原理上补偿上述误差。西北工业大学的刘诗斌博士等人提出了椭圆到圆的补偿方法，但也只能提高水平放置状态下的电子罗盘航向精度［2～4］。

本文提出了由椭球到圆球的补偿方法，将电子罗盘补偿技术由平面拓展到了三维空间。通过姿态误差矩阵将磁传感器测量到的地磁场矢量和由椭球补偿到圆球，提高了大倾角情况下的电子罗盘航向精度。

无论从控制的实时性与准确性、工程设计的简便性还是成本体积来说都是一个很好的设计方案，并不需要采用复杂昂贵的标准设备，能够有效地应用到惯性导航、无人飞机飞行器等航空航天领域［5，6］。

1 电子罗盘原理

电子罗盘一般分为平面电子罗盘和三维电子罗盘两种，本文采用三维电子罗盘。

电子罗盘通过测量载体坐标系下的三轴地磁分量，通过补偿由俯仰和滚转角引起的误差，就可得到比较精确的方位角［7，8］，原理如图1 所示。

图1 电子罗盘原理示意图Fig 1 Principle of electronic compass

其中，ψ，θ，γ 分别为椭球模型相对于圆球模型的航向、俯仰、滚转角。

补偿公式如下

其中

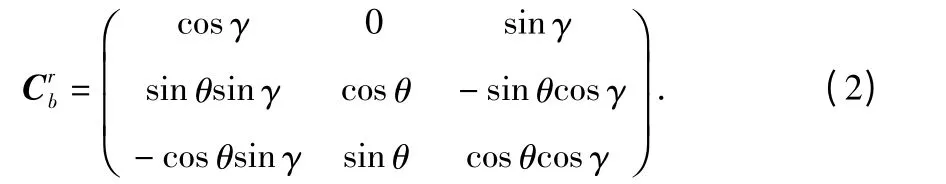
航向角可由式(2)得到

2 由椭球到圆球的补偿算法

电子罗盘往往因为环境的磁干扰或者安装误差的影响使得磁传感器三个轴向测量得到的地球磁场矢量和模型不是一个圆而是一个椭球，并且这个椭球的长轴、短轴等并不与东北天坐标系重合，带有航向、倾角误差［9］，使得难以采用式(3)补偿得到精确的航向角。椭球模型如图2 所示。

可以采用欧拉旋转将带有航向、倾角误差的椭球变化为长轴、短轴等与东北天坐标系重合的标准椭球，然后再进行线性变化将椭球变为圆球［10，11］。欧拉旋转原理如图3所示。

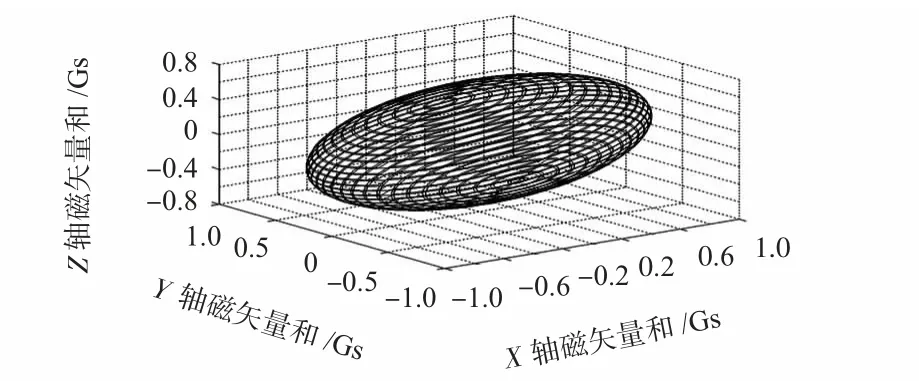
图2 磁传感器测量得到的三轴地磁矢量和模型Fig 2 Triaxial geo magnetic vector sum model measured by magnetic sensors

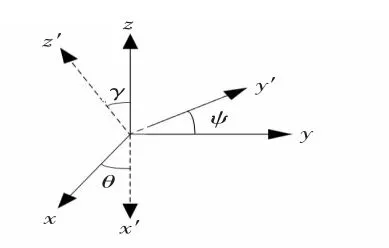
图3 欧拉旋转示意图Fig 3 Diagram of Euler rotation

图3 中，ψ，θ，γ 分别为椭球模型相对于圆球模型的航向、俯仰、滚转误差角。

xyz 坐标系为标准圆球坐标系，x'y'z'为椭球坐标系，［x y z］为磁场在圆球坐标系中的分量;［x0y0z0］为磁场在椭球坐标系下的分量;C 为坐标系x'y'z'到xyz 坐标系的转换矩阵，如式(4)、式(5)所示

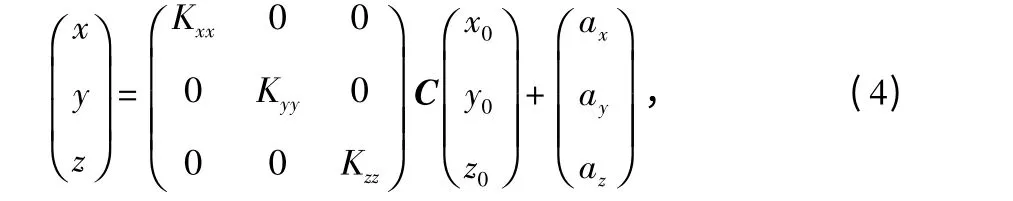
圆球的标准方程可以写为

将式(5)带入式(4)得

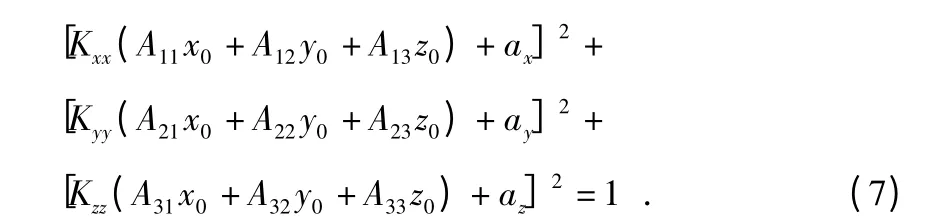
式(7)可以化简为

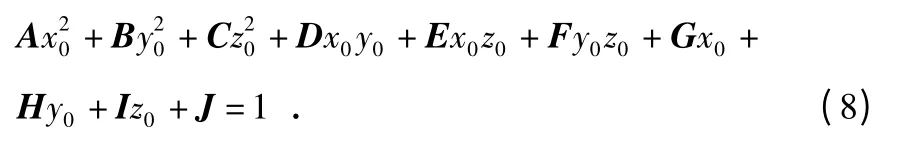
其中

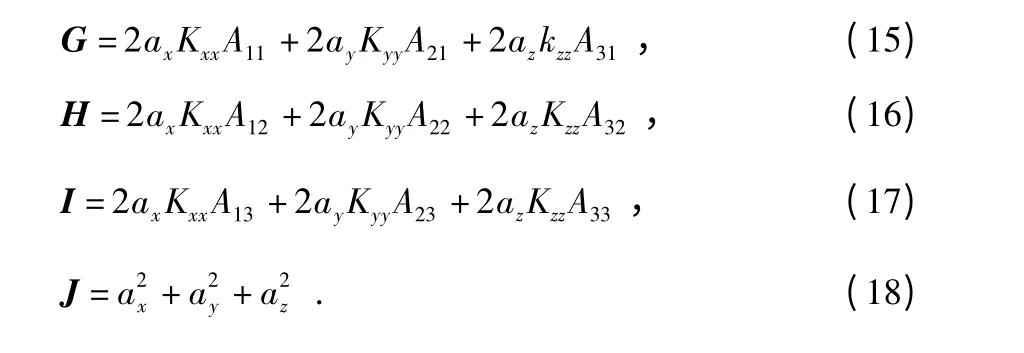
根据惯性导航相关的知识可知，对于欧拉旋转矩阵存在下面的关系

并且，实际上矩阵A 中只存在3 个变量即ψ，θ，γ，因此令

将式(22)带入式(5)得

式(23)是一个典型的非线性方程组，可以通过数值计算方法求的各参数的解。本文通过最快下降法求得各参数的解的范围后，通过牛顿法得到了比较精确的解值，并编制了相应的Matlab 程序。

3 硬件设计

为了验证补偿算法的有效性，设计了一种低成本的电子罗盘。硬件采用STM31F103 作为主处理器，MPU6050 加速度传感器和HMC5883L 地磁传感器作为敏感头。硬件框图如图4 所示。

STM32F103 负责分别读取MPU6050，HMC5883L 的加速度、磁信息，供电模块采用线性电压变换芯片将USB 接口提供的+5V 电源变为3.3V 为处理器和传感器供电。

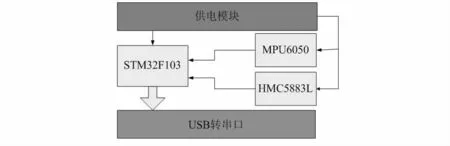
图4 电子罗盘硬件框图Fig 4 Hardware block diagram of electronic compass

USB 转串口采用CP2102，这是一种USB 转RS—232 芯片，具有很好的性价比。实物图如图5 所示。

图5 电子罗盘实物Fig 5 Physical map of electronic compass

4 实验验证

性能验证实验采用位置转台，其精度为2"，可以认为没有误差。

图6 是采集到的磁传感器的三轴矢量和的原始模型在XY 平面上的投影，可以看出，投影不是一个标准的圆球，它的两极在投影面并不重合;图7 是经过本方法补偿后的三轴矢量和在XY 面的投影，经过本文提出的椭球到圆球的补偿后，两极已经基本重合，两轴也基本等长。

如表1 所示，列出了未补偿的电子罗盘航向角和补偿后的电子罗盘航向角对比。

表1 只是选取了一个固定航向角度情况下的数据，实际上补偿后的电子罗盘在转台出于任意一航向角情况下，在－80°～+80°倾角情况下，航向误差不大于3°，而补偿前的误差最大达到20°左右。

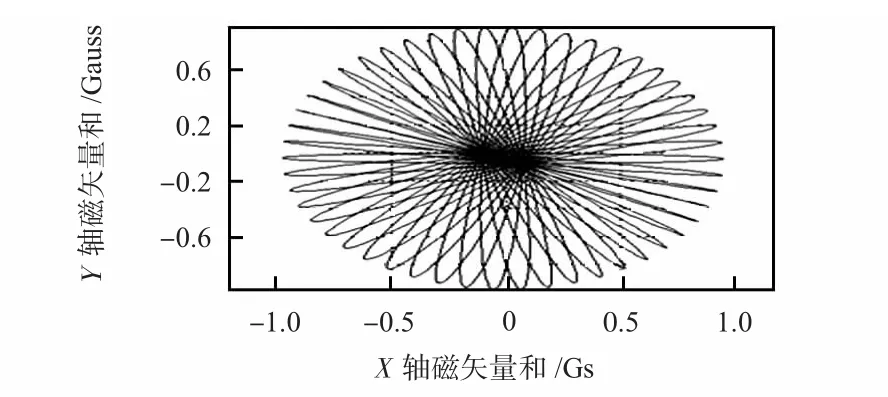
图6 补偿前的三轴磁矢量和Fig 6 Triaxial magnetic vector sum before compensation

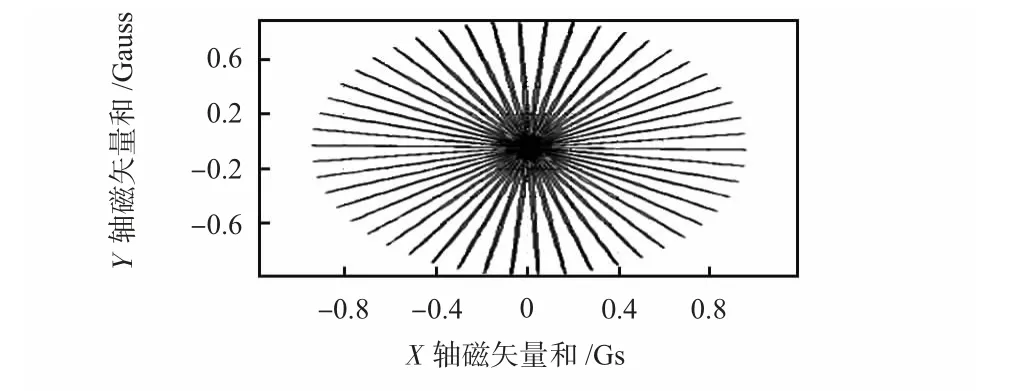
图7 补偿后的三轴磁矢量和Fig 7 Triaxial magnetic vector sum after compensation

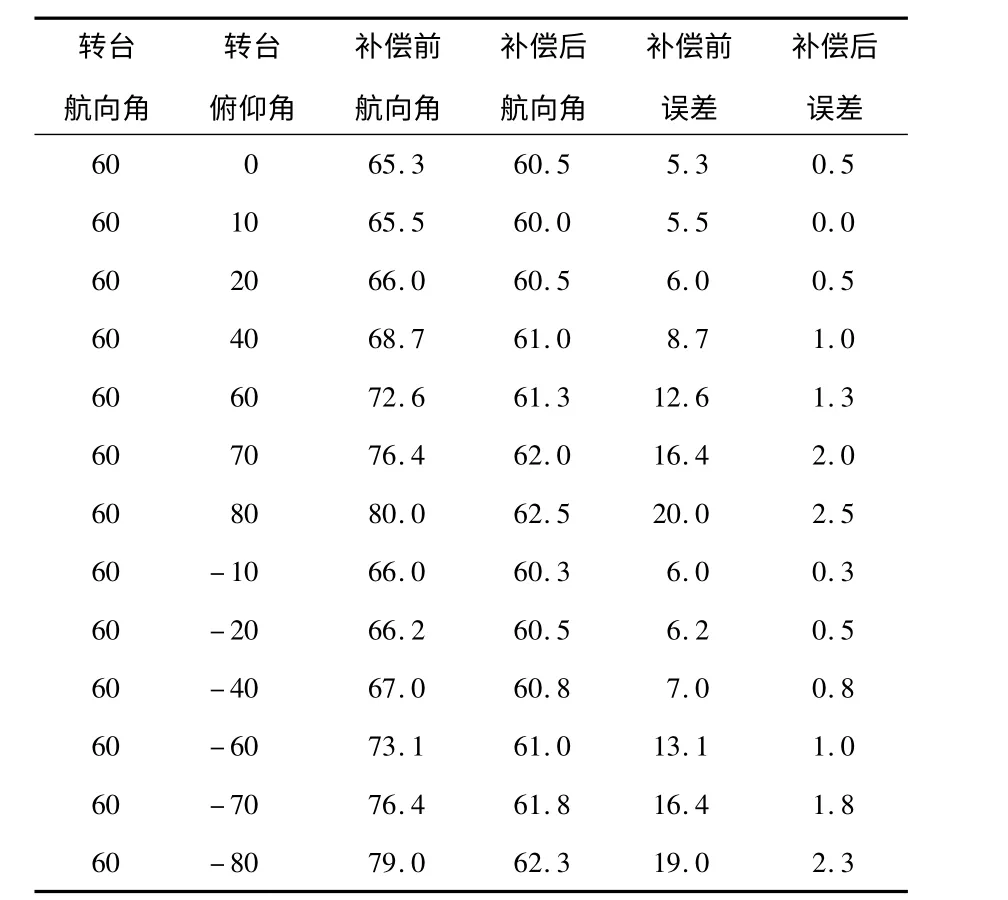
表1 补偿实验结果(单位:(°))Tab 1 Compensation experiment results(Unit:(°))

5 结 论

本文提出的由椭球到圆球的磁传感器补偿技术，经过实验证明:该方法可以有效地补偿电子罗盘在大倾角情况下的航向角误差，并且该方法可以与磁传感器的椭球拟合标定同时进行，不需要采用专业设备，通过手持旋转多个位置就可实现，有利于减少测试时间、减少成本支出，非常适合低成本的惯性导航、人体姿态测量以及机器人定位定向等领域。

［1］ 龙 礼，张 合.三轴地磁传感器误差的自适应校正方法［J］.仪器仪表学报，2013，33(1):161－165.

［2］ 刘诗斌，冯晓毅，李 宏.基于椭圆假设的电子罗盘误差补偿方法［J］.传感器技术，2002，21(10):28－33.

［3］ 杨 芳.基于MEMS 的惯性导航系统算法研究与仿真［D］.沈阳:沈阳理工大学，2007.

［4］ 刘哥群，薛荛舜.磁航向传感器在无人机飞行控制系统中的应用［J］.传感器技术，2003，22(12):54－56.

［5］ 张 炜，程锦房.一种三轴磁传感器正交误差校正的简便方法［J］.兵工自动化，2009，28(12):75－78.

［6］ Paul Leliak.Identification and evaluation of magnetic field sources of magnetic airborne detector equipped aircraft［R］.［s.l.］:IRE Trans Aerosp Navig Electron，1961.

［7］ 刘大鹏，马晓川，朱 昀.基于磁阻传感器的电子罗盘设计［J］.微计算机应用，2008，29(5):97－100.

［8］ Timo Pylvanainen.Automatic and adaptive calibration of 3D field sensor［J］.Applied Mathematical Modeling，2008，32(4):575－587.

［9］ 戴 磊，齐俊桐，吴 冲.旋翼飞行机器人磁罗盘误差分析及校准［J］.机器人，2009(4):418－423.

［10］张爱军，王昌明，赵 辉.三轴电子罗盘的磁航向角误差补偿研究［J］.传感器与微系统，2012，34(4):33－35.

［11］苑海静.船用MEMS 航姿测量系统算法研究与实现［D］.哈尔滨:哈尔滨工程大学，2010.