内外压复合作用下5A02铝合金管材的硬化行为

崔晓磊，王小松, ，苑世剑,

(1. 哈尔滨工业大学 金属精密热加工国家级重点实验室，哈尔滨 150001；2. 哈尔滨工业大学 材料科学与工程学院，哈尔滨 150001)

近年来，内高压成形技术已经成为汽车、航空航天等领域制造复杂空心变截面构件的最主要的一种轻量化成形技术。而准确测试和评价管材的成形性和力学性能是进行有限元分析并制定合理工艺参数的重要依据[1]。目前，测试管材力学性能的方法主要有单向拉伸试验[2]、整管拉伸试验[2]、环向拉伸试验[3]和液压胀形试验[4]。内高压成形用管材直径较大，所以，整管拉伸测试方法不太现实，最常用的方法是沿管材轴向切取弧形试样进行单向拉伸来测试管材的力学性能。然而，轴向试样单向拉伸只能反映管材轴向的力学性能而无法反映管材的环向性能，而在内高压成形中管材主要以环向变形为主。在此基础上人们提出了利用环向拉伸测试管材的力学性能，但是由于环向试样与D型块之间存在摩擦，所以测试得到的强度往往偏高[3, 5-6]。

在常规的内高压成形中，通常忽略法向应力而将管材假设在平面应力状态下发生变形，国内外学者为了得到双向应力状态下管材的应力-应变曲线对管材的液压胀形进行了大量的研究[7-12]。为了获得管材液压胀形过程中的等效应力与等效应变，需要在胀形过程中测试管材胀形区最高点处的高度、壁厚以及胀形区的轴向曲率半径[11-12]。轴向曲率半径的测量是一个难题，通常将管材胀形区轮廓形状假设为余弦函数、圆弧或者抛物线，忽略入口边界圆角的影响[13-14]。然而，HUANG 等[8-10]和何祝斌等[15]研究发现，将胀形区轮廓线假设为椭圆形且与模具圆角相切，计算得到的椭圆轮廓线与管材实际轮廓线更加吻合。HE等[16]假设管材胀形区为椭圆轮廓，首次发现了胀形过程中管材最高点处的壁厚线性模型，认为管材在胀形过程中最高点处的壁厚与胀形高度基本符合线性关系，并利用SUS409和AA6011等多种管材在不同长径比条件下得到了验证。

迄今为止，所有的管材液压胀形测试都是在平面应力状态的假设条件下进行计算的。然而，近年来众多学者为提高管材的成形性提出了管材双向加压成形的概念，即在管材的内部和外部同时施加高压的液体，使管材在内外压力差的作用下发生变形[17-19]。早在1966年FUCHS等[17]通过在管材内外同时施加液体压力，使得管材的成形性显著提高。JAIN等[20-21]根据MELLOR提出的方法研究了管材在不同加载条件下的塑性失稳，得到了均匀塑性变形结束时的临界应变，在无轴向补料和有轴向补料情况下，在管材外部施加液压均可以提高其成形极限。GUVEN[22]针对外压对薄壁管材塑性失稳的影响进行了研究，考虑3种不同的颈缩准则，得到了考虑法向应力影响的环向极限应变ε1L和轴向极限应变ε2L。

当管材在内外双向压力下发生变形时，管材不再处于平面应力状态，而必须按照三维应力状态进行处理。迄今为止，由于内外同时加压的实验装置较难实现，还没有实验研究管材在三维应力状态下的硬化行为。只有哈工大液力成形中心建立了管材的双向加压实验装置，并在此基础上进行了内外压复合作用下管材的自由胀形以及圆角填充行为研究[23-24]。

为了研究管材在内外压复合胀形三维应力状态下的硬化行为，本文作者首先理论推导得到了三维应力状态下管材应力应变分析模型。然后在已建立的双向加压实验装置上进行了 5A02铝合金管材的内外压复合胀形实验，初步得到了 5A02铝合金管材在内外压复合作用下的胀形区轮廓形状、壁厚分布以及其等效应力-应变曲线。

1 管材内外压复合胀形原理

传统管材液压胀形时管材仅受到内压的作用，此时由于内压作用于管材厚度方向产生的法向应力与面内应力相比较小，通常简化为平面应力状态。

管材内外压复合胀形是在传统管材液压胀形的基础上同时向管材外部施加高压液体，使管材在内外压力差的作用下发生胀形，其原理示意图如图1所示。在管材内外压复合胀形中，由于管材厚度方向所受的内外压力较高而不能忽略法向应力的影响，管材所受的应力由传统的面内双拉应力状态转变为面内双拉、厚向受压或三向全部受压的三维应力状态。

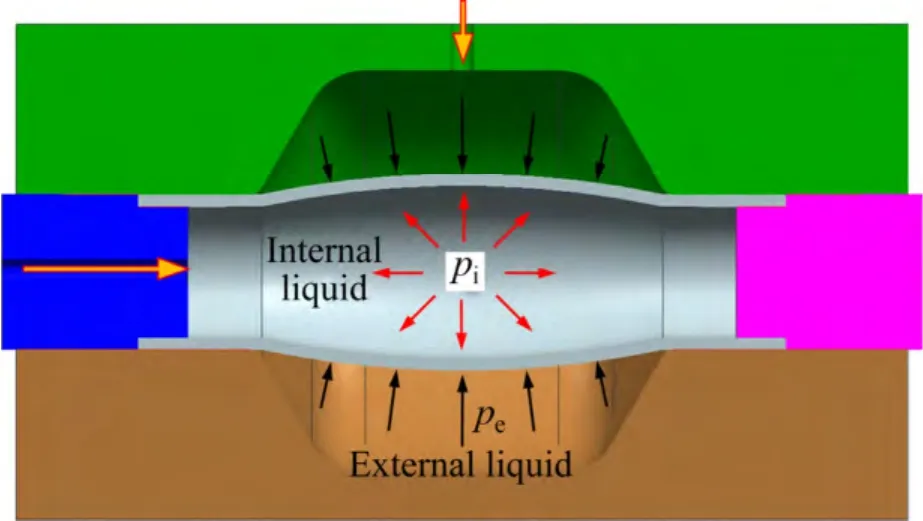
图1 管材内压(pi)和外压(pe)复合胀形原理示意图Fig. 1 Schematic diagram of tube bulging under combined action of internal (pi) and external pressure (pe)

2 内外压复合作用下应力应变理论模型

2.1 应力分析

管材在内外压复合作用下发生胀形，必须按照三维应力状态进行处理。为了求解管材的环向应力，取胀形区最高点的一个微小区域，如图2所示，由厚度方向的力学平衡条件可推导得到：

式中：ρφ和ρθ分别表示管材胀形区最高点p处中性层的轴向和环向曲率半径；σφ和σθ分别表示管材胀形区最高点的轴向和环向应力；pi和pe分别表示管材受到的内压和外压，tp为管材胀形区最高点的壁厚。

整理式(1)可得式(2)：

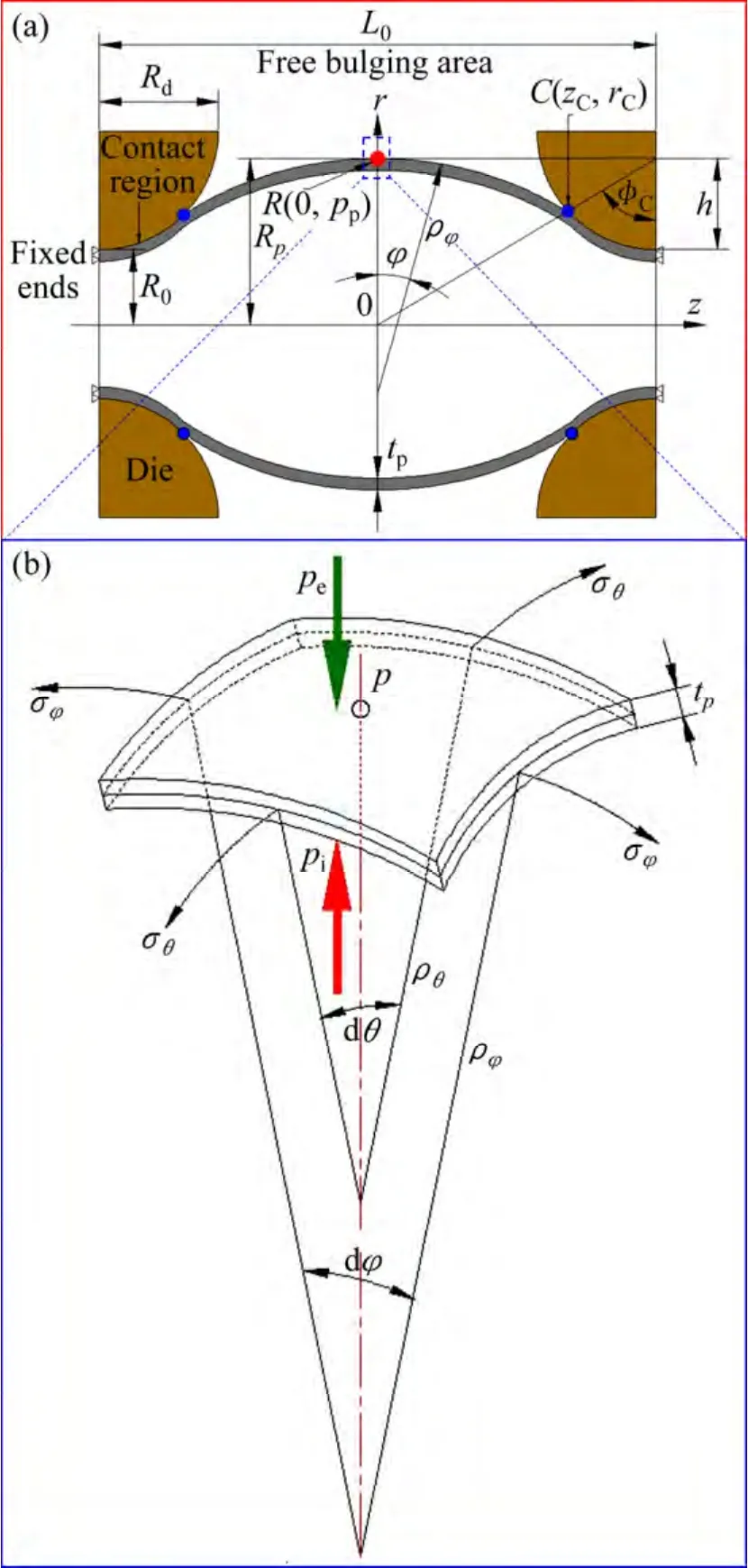
图2 管材内外压复合胀形过程力学平衡Fig. 2 Mechanical equilibrium during tube bulging under combined action of internal and external pressure: (a)Geometrical shape of die and tube; (b) Stress analysis at highest point p of bulging zone

根据文献[8]中的相关推导，考虑厚度影响，可以得到管材胀形区最高点处中性层的环向轴向的曲率半径 ρθ和 ρφ分别为

式中：Rp为轮廓椭圆的短半轴，即最高点p处的外半径；R2为轮廓椭圆的长半径。

此外，由胀形区最高点处轴线方向的力学平衡方程可以求得管材最高点处轴向的应力(φσ)(等同于两端封闭的情况)。

将式(5)代入式(2)中，即可求得胀形区最高点处管材的环向应力(θσ)：

管材胀形区最高点处的法向应力在管材的内表面等于内压pi，在管材的外表面处等于外压pe，在中性层处为

2.2 应变分析

对于管材胀形区最高点处的应变，环向应变(εθ)和厚度方向应变(εθ)可以分别表示为

式中：R0与t0分别为管材的初始外半径与初始壁厚；h为管材的胀形高度。管材胀形区最高点处的轴向应变(εφ)可以由体积不变条件求得

2.3 等效应力应变及硬化方程

在计算管材的等效应力与等效应变时，假设管材为各向同性材料，且忽略弹性应变的影响。对于内外压复合作用下的管材，必须按照三维应力状态处理。所以其等效应力可以表示为

通过测定管材的一些初始参数以及胀形过程中管材所受的内压、外压以及胀形高度等，即可根据上述理论分析得到管材的等效应力和等效应变。

很多金属的硬化曲线近似于抛物线形状，对于立方晶格的退火金属(如钢板和铝合金等)，其等效应力-等效应变曲线都可相当精确地用 Hollomon的指数型硬化方程来表示：

式中：K为强度系数。

3 5A02铝合金管材内外压复合胀形实验研究

3.1 实验材料

所用材料为5A02-O铝合金管材，其外径和名义壁厚分别为63和2 mm。沿管材轴向切取弧形拉伸试样后在电子万能材料试验机 Instron5569上进行单向拉伸测试，得到的真应力-真应变曲线如图 3所示。表1所列为单向拉伸得到的管材轴向力学性能参数。

图3 5A02铝合金管材轴向真实应力-应变曲线Fig. 3 True stress-strain curve of 5A02-O aluminum alloy tubes along axial direction

表1 5A02铝合金管材轴向力学性能参数Table 1 Mechanical property parameters of 5A02-O aluminum alloy tubes along axial direction

3.2 实验装置

管材内外压复合胀形的实验装置如图4所示。实验模具主要由外筒、芯轴、模具型腔、夹紧块和底板组成。不同于传统的由上模、下模和左右冲头组成的内高压成形模具，将本模具设计成闭式的圆筒形结构，易于实现外压的密封。内压的密封由管材和芯轴之间的O型密封圈实现，外压的密封由芯轴和底板以及外筒和底板之间的O型密封圈实现。

图4 管材内外压复合胀形实验装置Fig. 4 Experimental setup of tube hydroforming under combined action of internal and external pressures

在原有 10 MN内高压成形机的基础之上进行更新，建立管材内外压复合胀形实验装置。原先的内压增压器提供管材的内压，另外增加一个增压器提供管材的外压。这两个增压器可以同时由伺服阀进行控制。同时，控制系统也进行了更新，引入一个新的双向加压控制界面。

当进行管材内外压复合胀形实验时，内压增压器通过芯轴上的内压入口将高压液体充入管材的内部，外压增压器通过外筒上的外压入口将高压液体施加在管材的外部。最重要的是，这两个独立的增压器可以由两个伺服阀耦合在一起，从而达到精确的伺服控制。两个伺服阀接收来自控制系统发出的信号。所以，内压和外压可以通过预先输入控制系统的加载路径实现精确的加载与卸载。此外，变形过程中为了防止底板和外筒发生分离，从而造成外压的泄漏，必须施加一定的合模力。

3.3 实验方案

内外压复合胀形实验初始管材及模具的具体参数如表2所列。

表2 初始管材及模具参数Table 2 Initial parameters of tubes and die

管材胀形过程中需要测量管材的内压pi、外压pe以及最高点胀形高度h以及胀形区最高点壁厚tp。然而，当管材在内外压复合作用下进行胀形时，由于外部高压液体的存在，管材的胀形高度很难进行实时测量。所以，本研究中初步采用多点拟合的方式，即利用多根管材分别进行不同变形量的内外压胀形实验，本研究中采用4根管材，测量并记录4个中间状态时刻管材的胀形高度和最高点壁厚，然后根据上节中的理论推导即可得到管材在内外压复合作用下的应力应变关系。本实验中采用的外压为85 MPa (1.0σs)，内压取4个中间状态，最后一个对应于管材破裂状态。

4 结果与讨论

图5所示为外压为85 MPa时胀形得到的不同胀形高度的5A02铝合金管材试样，4个中间状态管材试样的胀形高度分别为1.06 mm、1.50 mm、2.38 mm和3.68 mm。实验中得到这4根不同胀形高度管材试样的内压与外压数值如表3所列。

图5 外压为85 MPa时不同胀形高度的管材照片Fig. 5 Photos of bulged tubes with different bulging heights under external pressure of 85 MPa

表3 管材内外压力值及胀形高度Table 3 Internal pressure, external pressure and bulging height

图6 外压85MPa时管材胀形区椭圆轮廓形状Fig. 6 Elliptical profile of bulging zone under external pressure of 85 MPa

4.1 胀形区轮廓形状

对不同中间状态的管材的直径进行测量，即可得到其胀形区的轮廓形状尺寸，如图6所示。在Origin根据上述2.1节的理论推导即可得到管材胀形区最高中对4组轮廓形状数据分别用椭圆函数进行拟合，拟合得到的决定系数 R2值分别为 0.956、0.961、0.978和0.995。由此可以发现，5A02铝合金管材在内外压复合条件下进行胀形时，其胀形区轮廓可以非常准确地用椭圆函数来进行拟合，且随着胀形高度的增加管材胀形区轮廓形状越接近椭圆形。在管材内外压复合胀形过程中，假设管材胀形区形状符合椭圆几何模型，点处的应力状态。

4.2 壁厚分布

文献[16]在研究管材内压胀形时提出了壁厚线性模型，认为管材在两端固定的条件下进行胀形时，管材胀形区最高点处的壁厚与胀形高度成线性关系，如式(14)所示：

式中：b为常数。

在管材内压胀形过程中，胀形高度h很容易进行实时测量，只要知道常数b值，即可计算胀形过程中每一时刻的壁厚，最后根据前述的理论推导即可计算得到管材的应力-应变曲线。对于本研究中管材内外压复合胀形，由于外部高压液体的存在，管材胀形高度的实时测量非常困难，所以在本实验中将中间4个中间状态管材的胀形高度和壁厚分别进行测量，结果如图7所示。

由图7可以发现，在管材内外压复合胀形中，管材胀形区最高点处壁厚与胀形高度同样存在着线性关系。对4个实验点进行线性拟合，即可得到最高点壁厚与胀形高度的线性关系为

另外，由式(14)可以发现，常数 b可以由下式得到：

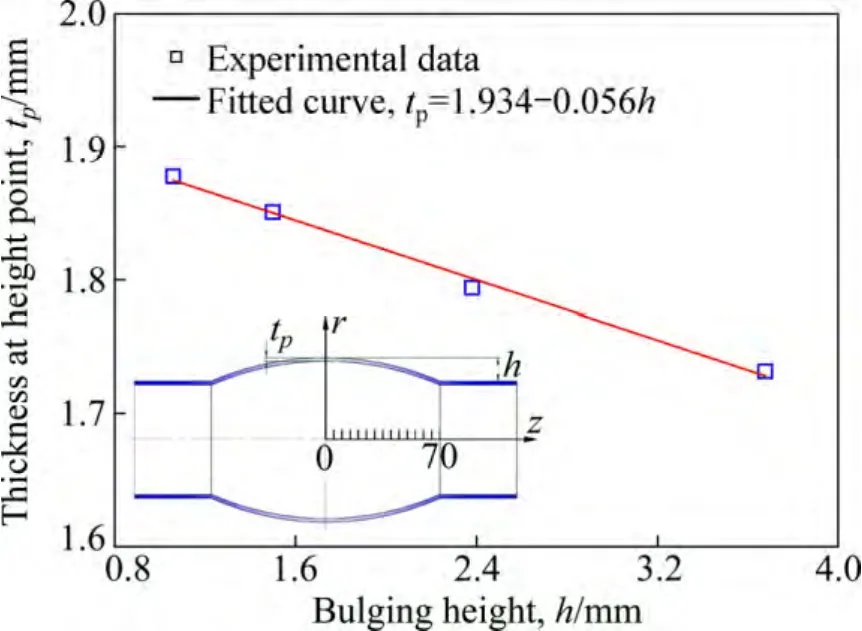
图7 外压为85 MPa时管材胀形区最高点处壁厚与胀形高度的线性关系Fig. 7 Linear relationship between thickness at highest point in bulging zone and bulging height and bulging height under external pressure of 85 MPa

式中：tend和hend分别为胀形破裂时管材的最高点壁厚和胀形高度。用最后一个状态的管材数据进行求解 b值，其中测试点处管材原始实际壁厚为1.935 mm，得到的b值为0.0553，则由此得到的壁厚线性模型为

由式(17)可以发现：由此得到的壁厚线性关系与直接测量得到的壁厚线性关系(见式(15))基本一致，如果内外压复合胀形过程中可以解决实时测量胀形高度的难题，只需测量胀形最终管材的壁厚即可根据前述理论推导得到管材在内外压复合作用下的应力-应变关系。

4.3 硬化曲线

将上述实验测量得到的管材的内压、外压、胀形高度以及最高点壁厚数值代入第2节中的应力应变理论推导公式，即可得到外压为85 MPa情况下5A02铝合金管材的等效应力-应变关系曲线，如图 8所示。其硬化方程如式(18)所示

由图8及式(18)可以发现，5A02铝合金管材在内外压复合胀形条件下得到的等效应力-应变曲线的硬化指数n值为0.274，相比于轴向弧形试样单向拉伸得到的n值(0.304)发生了降低。这是因为无缝管材的轴向和环向性能不可避免地存在差异，环向的性能相对于轴向的性能稍弱一些，所以三维应力状态下测试得到的管材的应力应变曲线比轴向单向拉伸测试得到的应力应变曲线稍低一些，而n值发生了降低。

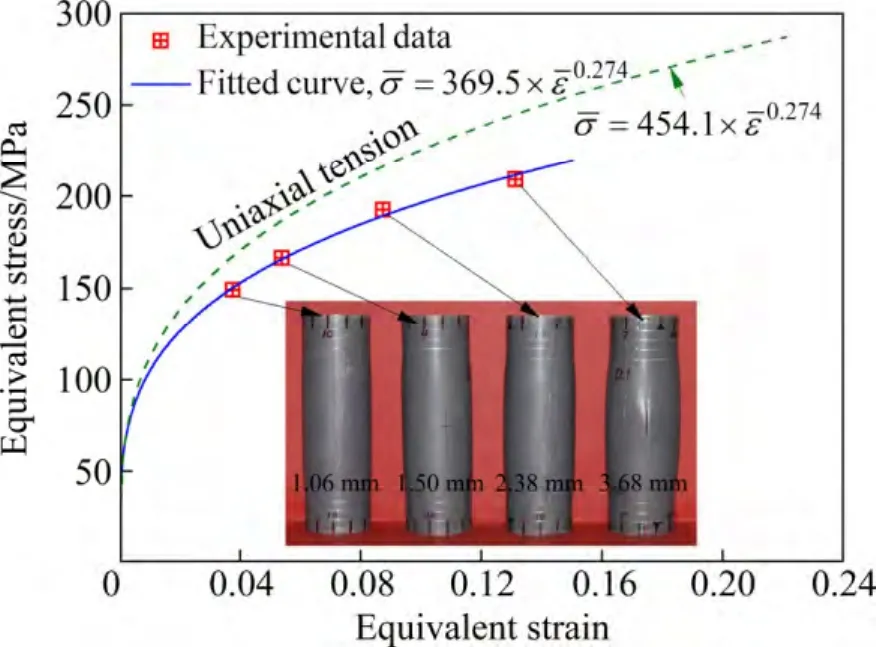
图8 外压为85 MPa管材胀形得到的等效应力-应变曲线Fig. 8 Equivalent stress-strain curve obtained from double-sided tube bulging at external pressure of 85 MPa

5 结论

1) 理论推导得到了内外压复合作用下管材的应力应变分析模型，值得注意的是求解力学平衡方程时必须考虑厚度的影响，求解得到的环向应力与轴向应力必须包含厚度项。

2) 外压为85 MPa时，管材在胀形过程中其胀形区轮廓形状可以用椭圆函数进行拟合，其最高点壁厚与胀形高度符合线性关系。

3) 通过实验得到了外压为85 MPa时5A02铝合金管材的硬化曲线(等效应力-应变曲线)，其得到的n值为0.274，低于单向拉伸得到的0.304。这是因为无缝管材的轴向和环向性能不可避免地存在差异，环向的性能相对于轴向稍弱一些，所以三维应力状态下测试得到的应力应变曲线比轴向单向拉伸测试得到的应力应变曲线稍低一些，致使n值降低。

4) 对于双向加压的内高压胀形工艺，采用由内外液压胀形得到的等效应力-应变曲线更能准确反映管材在内高压成形中的真实受力状态，肯定会使结果预测精度更高。然而，目前液压胀形测试管材力学性能的方法也存在一些缺点，如测试过程较单向拉伸更加复杂，但相信随着测试技术的不断发展，这些问题都会迎刃而解。

[1] 苑世剑, 何祝斌, 刘 钢, 王小松, 韩 聪. 内高压成形理论与技术的新进展[J]. 中国有色金属学报, 2008, 18(10):2523-2533.YUAN Shi-jian, HE Zhu-bin, LIU Gang, WANG Xiao-song,HAN Cong. New developments in theory and processes of internal high pressure forming[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(10): 2523-2533.

[2] GB/T 228.1-2010. 金属材料—拉伸试验-第 1部分: 室温试验方法[S].GB/T 228.1-2010. Metallic materials—Tensile testing: Part 1:Method of test at room temperature[S].

[3] LIN Y L, HE Z B, YUAN S J, WU J. Formability determination of AZ31B tube for IHPF process at elevated temperature[J].Transactions of Nonferrous Metals Society of China, 2011, 21:851-856.

[4] FUCHIZAWA S, NARAZAKI M. Bulge test for determining stress-strain characteristics of thin tubes[C]//WANG Z R, HE Y X. Proceedings of the Fourth International Conference on Technology of Plasticity. Beijing: International Academic Publisher, 1993, 1: 488-493.

[5] JIANG L, JONAS J J, BOYLE K, MARTIN P. Deformation behavior of two Mg alloys during ring hoop tension testing[J].Materials Science Engineering A, 2008, 492: 68-73.

[6] 何祝斌, 苑世剑, 查微微, 梁迎春. 管材环状试样拉伸变形的受力和变形分析[J]. 金属学报, 2008, 44(4): 423-427.HE Zhu-bin, YUAN Shi-jian, CHA Wei-wei, LIANG Ying-chun.Force and deformation analysis of tube ring specimen during hoop tension test[J]. Acta Metallurgica Sinca, 2008, 44(4):423-427.

[7] SOKOLOWSKI T, GERKE K, AHMETOGLU M, ALTAN T.Evaluation of tube formability and material characteristics:hydraulic bulge testing of tubes [J]. Journal of Materials Processing Technology, 2000, 98: 34-40.

[8] HWANG Y M, LIN Y K. Evaluation of flow stresses of tubular materials considering anisotropic effects by hydraulic bulge tests[J]. Journal of Engineering Materials and Technology, 2007,129(3): 414-421.

[9] HWANG Y M, WANG C W. Flow stress evaluation of zinc copper and carbon steel tubes by hydraulic bulge tests considering their anisotropy[J]. Journal of Materials Processing Technology, 2009, 209: 4423-4428.

[10] HWANG Y M, LIN Y K, ALTAN T. Evaluation of tubular materials by a hydraulic bulge test[J]. International Journal of Machine Tools and Manufacture, 2007, 47(2): 343-351.

[11] BORTOT P, CERETTI E, GIARDINI C. The determination of flow stress of tubular material for hydroforming applications[J].Journal of Materials Processing Technology, 2008, 203:381-388.

[12] YANG L F, GUO C. Determination of stress-strain relationship of tubular material with hydraulic bulge test[J]. Thin-Walled Structures, 2008; 46: 147-154.

[13] STRANO M, ALTAN T. An inverse energy approach to determine the flow stress of tubular materials for hydroforming applications[J]. Journal of Materials Processing Technology,2004, 146(1): 92-96.

[14] 李泷杲. 金属薄壁管液压成形应用基础研究[D]. 南京: 南京航空航天大学, 2007.LI Long-gao. Fundamental study on tube hydroforming process[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007.

[15] 林艳丽, 何祝斌, 苑世剑. 管材自由胀形时轮廓区轮廓形状的影响因素[J]. 金属学报, 2010, 46(6): 729-735.LIN Yan-li, HE Zhu-bin, YUAN Shi-jian. The factors affecting the profile of middle bulging region during tube bulging test[J].Acta Metallurgica Sinca, 2010, 46(6): 729-735.

[16] HE Z B, YUAN S J, LIN Y L, WANG X S, HU W L. Analytical model for tube hydro-bulging tests, part II: Linear model for pole thickness and its application[J]. International Journal of Mechanical Sciences, 2014, 87: 307-315.

[17] FUCHS F J. Hydrostatic pressure: its role in metal forming[J].Mechanical Engineering, 1966, 88(4): 34-40.

[18] SMITH L M, GANESHMURTHY S, ALLADI K. Double-sided high-pressure tubular hydroforming[J]. Journal of Materials Processing Technology, 2003, 142(3): 599-608.

[19] JAIN N, WANG J, ALEXANDER R. Finite element analysis of dual hydroforming processes[J]. Journal of Materials Processing Technology, 2004, 145(1): 59-65.

[20] JAIN N. Modeling and analysis of dual hydroforming process[D].Texas: Texas A&M University, 2003: 47-66.

[21] JAIN N, WANG J. Plastic instability in dual-pressure tube-hydroforming process[J]. International Journal of Mechanical Sciences, 2005, 47(12): 1827-1837.

[22] GUVEN U. Effect of the external pressure on the plastic instability of thin-walled tubes[C]//Proceedings of the Institution of Mechanical Engineers, Part B. Journal of Engineering Manufacture, 2009, 223: 1361-1365.

[23] CUI X L, WANG X S, YUAN S J. Deformation analysis of double-sided tube hydroforming in square-section die[J]. Journal of Materials Processing Technology, 2014, 214(7): 1341-1351.

[24] CUI X L, WANG X S, YUAN S J. Experimental verification of the influence of normal stress on the formability of thin-walled 5A02 aluminum alloy tubes[J]. International Journal of Mechanical Sciences, 2014, 88(11): 232-243.