基于最小梯度支撑的2.5D井地电位法正则化聚焦反演

张志勇，周 峰，李泽林

(1.中南大学 地球科学与信息物理学院，长沙 410083；2.东华理工大学 核资源与环境教育部重点实验室，南昌 330013)

直流电阻率法是矿产资源勘查、水资源调查的常用方法之一，近年来特别是在环境与工程地球物理中得到广泛应用。直流电阻率方法采用地表观测，通过视电阻率曲线或拟断面图对地下目标体进行推断解释。在某些情况下，由于测区、目标体电阻率差异的限制，严重影响探测深度与分辨率，井地电法由于井中电极的引入，大大改善了传统方法的不足，但是井地电位方法难于采用视参数拟断面图表示，因此，资料解释更依赖反演技术，当前井地电位正演与反演成为了研究的热点[1-6]。SCRIBA[7]和SPITZER[8]利用边界元法实现了三维井地电位正演模拟；PRIDMORE等[9]利用有限元法实现三维井地电位正演模拟；徐凯军等[10]和王志刚等[11]采用有限差分实现了垂直线源井地电位法三维正演模拟；戴前伟等[12]进行了井地电位2.5有限元数值模拟异常分析；柳建新等[13]进行了坑道内的聚焦超前探测电阻率法有限元数值模拟研究；LI等[14]进行了地面和井中观测数据的三维反演研究；柯敢攀等[15]应用非线性阻尼最小二乘迭代算法实现了井地电法的三维正反演研究；吕玉增等[16]采用了共轭梯度法求解最小二乘目标函数实现了井地三维激电数据的快速反演；王志刚等[17]实现了Born近似快速三维井地电法数据的反演；安然等[18]实现了井地三维电阻率反演。

众所周知，地球物理反问题存在不稳定性与多解性，正则化方法是得到稳定解的重要方法之一。正则化方法通过在反演目标函数中引入稳定因子，对模型解空间进行约束，减少反问题的不适定性。地球物理中常用的稳定因子形式有：最小模型约束、最大平滑模型约束、模型总变化量约束、最小支撑约束、最小梯度支撑约束等。CONSTABLE等[19]、SMITH等[20]和ZHDANOV等[21-22]成功地将最大平滑模型约束应用到地球物理反演解释，其中，以CONSTABLE等[19]和DEGROOT-HEDLIN等[23]提出的OCCAM反演算法应用最为广泛。RUDIN等[24]在对图像边界的识别研究中提出了模型总变化量约束，该方通过模型参数梯度在定义域中L1范数最小进行约束，识别陡变边界；GAO等[25]将模型总变化量约束应用到生物荧光成像中；BURSTEDDE等[26]在一维全波场反演中也采用了模型总变化量约束；韩波等[27]结合模型总变化量和经典正则化方法的优点，实现了电阻率成像的混合正则化反演算法。为了减少随机的局部不均匀体，LAST等[28]提出最小体积支撑约束，应用于重力资料反演解释；之后GUILLEN等[29]和BARBOSA等[30]对这一方法进行改进，使约束条件具有方向性；CANDANSAYAR[31]、MEHANEE 等[32]和PORTNIAGUINE等[33]将其引入 MT数据反演；GRIBENKO等[34]将其用于CSEM三维反演；VIGNOOLI等[35]分析了最小支撑稳定因子中β取值对反演结果的影响。最小梯度支撑约束是一种有利突出陡变边界实现聚焦反演的约束形式，它是由PORTNIAGUINE等[36]提出并应用到地球物理反演中；之后，ZHDANOV等[37]实现了重力的聚焦反演；SALAH[38]同样将此方法应用到井间电磁模型反演；刘小军等[39]进行了二维大地电磁数据的聚焦反演算法研究。

反演是井电位法数据处理的核心，直接影响后期资料解释。为了提高陡变边界地质体的识别能力，本文作者采用最小梯度支撑的稳定因子实现了聚焦反演。为提高计算速度，采用了基于最小填入元思想的稀疏矩阵LDLT分解算法；为了快速精确选择正则化因子，研究“L-curve”改进算法，避免求曲线曲率过程中对离散数据求导引起的误差；采用重加权共轭梯度法(RRCG)求解正则化目标函数[36]，提高求解的稳定性与收敛速度，且该方法只需在初始迭代时选择一次正则化因子，在后面的迭代中自动调整。反演试算例表明，该方法具有较好的陡变边界识别能力和良好的应用前景。

1 井地电位正演理论

直流电阻率三维问题对地质体走向(z方向)进行傅里叶变换，得到2.5D井地电位的边值问题[40]，其表达式为

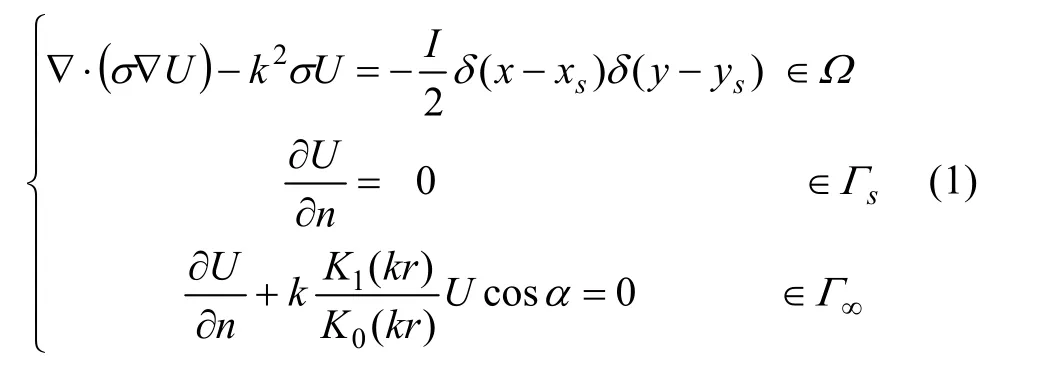
式中：区域Ω为二维研究区域；Γs、Γ∞为二维区域的边界(Γs为区域Ω的地表边界，Γ∞为区域Ω的地下边界)；σ为电导率；r为点电源到边界的距离；n为边界外法向方向；k为傅氏变换波数；α为边界外法向方向与供电点到边界矢量夹角；K0、K1分别为零阶、一阶第二类贝塞尔函数；(xs，ys)表示xy平面上的供电点坐标；δ(x)表示以x点为中心的一维狄拉克函数；I为供电点电流。

为了更好地模拟地下地质体的形态和提高正演计算的精度，采用了三角单元双二次插值有限单元法求解。式(1)的边值问题与求解式(2)的变分问题等价。

求解式(3)即可求得结点上傅氏域电位。通过傅里叶反变换得到电位u，研究工作采用八点滤波系数进行傅里叶变换及反变换，正变换系数(km)与反变换系数(gm)如表 1 所列[41]。

表1 傅氏变换系数km和gmTable 1 kmand gmparameters of Fouriers inverse transform

分析式(2)可知，如果将区域Ω分成目标区和边界区，目标区为异常体存在的区域，其网格步长采用等距剖分，边界区的网格步长采用指数递增的形式来模拟无穷边界。由于采用指数扩边，供电点到边界的矢径r相对计算区目标区足够大，因此，可采用目标区中心到边界的矢径近似，这样刚度矩阵只与波数有关，而与供电点无关。依据这一特点，为了提高计算的效率，结合基于图论理论的矩阵重排与填入元分析算法，设计了稀疏矩阵的LDLT分解算法。对于确定的剖分形式，只需一次基于最少填入元的符号分析[42]，对于同一波数只需一次LDLT分解算法，大大提高了正演的计算速度为反演研究奠定了基础，具体计算流程如图1所示。

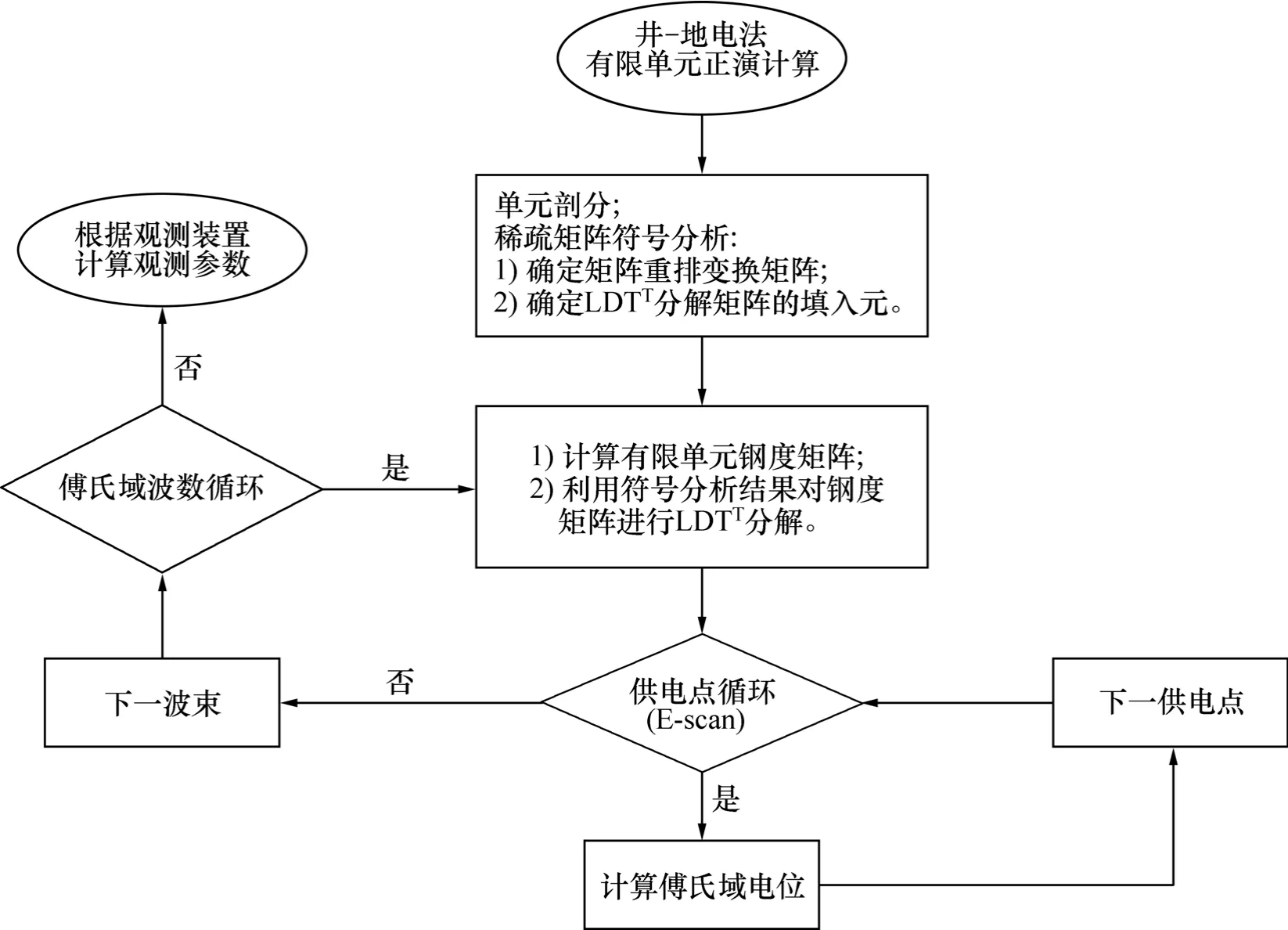
图1 井地电位有限单元正演计算流程Fig.1 Flow chart of borehole-surface electrical numerical simulation using FEM

2 井地电位聚焦反演

反演是井地电位资料解释的重要环节。为实现陡变边界地质体反演，研究了基于最小梯度支撑稳定因子的正则化反演技术。正则化因子的选择与目标函数的最优化求解是正则化反演的两个关键环节，本文作者在“L-curve”基础上提出了一种改进的“L-curve”方法，实现了正则化因子快速选择；采用RRCG方法求解反演目标函数，提高了反演过程的稳定性与计算效率。

2.1 基于最小梯度支撑的正则化反演

Tikhonov正则化，

式中：P(α，m)为目标函数；α为正则化因子(Regularization parameter)；φd(m)为数据目标函数；φm(m)为模型约束目标函数，也称稳定因子(stabilizer)[21]；m为模型参数。

通常采用实测数据与预测数据的距离来表示φd(m)，即

式中：dWˆ为数据权重矩阵；A(m)正演函数；d为观测数据。

ZHDANOV等[21]利用最小范数形式给出了一种稳定因子的统一表示形式。最小模型稳定因子是最常采用的稳定因子形式，它采用了当前模型和先验模型之差的L2范数。模型约束目标函数的表达式为

式中：mapr为先验模型；mWˆ为模型权重矩阵。如果以式(6)为标准形式，通过引入矩阵eWˆ则可以得到不同稳定因子的统一表示形式[33]。

为实现陡变异常体的边界反演，PORTNIAGUINE等[36]提出了最小梯度稳定因子：

式中：β为聚焦因子。分析可知，式(7)作为稳定因子将突出模型梯度的变化，从而实现聚焦反演。

为了利用式(7)统一表示稳定因子，采用式(7)构造模型权重函数：

式中：m(r)为模型参数分布函数；)(rm∇为模型参数梯度；e为与计算机数值精度有关的一个很小正数。

然后将式(5)、(6)和(8)代入到式(4)中，有

即可得到基于最小梯度支撑稳定因子的正则化反演目标函数。

2.2 重加权共轭梯度法(RRCG)

采用重加权共轭梯度法求解式(9)表示最优化问题，该方法在每一次迭代过程中利用前一次计算得到的模型向量重新计算权重矩阵 W ˆe，令Wˆe= W ˆen(mn)， mn为第n次迭代的模型向量。重加权共轭梯度法模型更新为

n度搜索方向向量。

式中： )(nmIα为第n步迭代的最速下降方向向量，可表示为

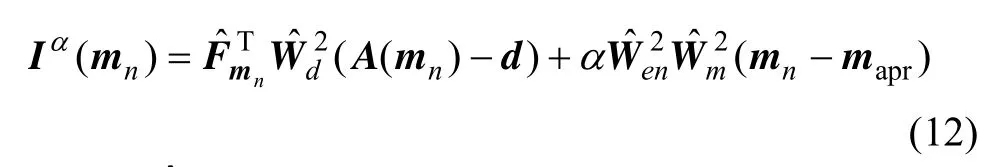
为确保式(10)每一次搜索目标函数充分下降，线性搜索的迭代步长为

为确保目标函数下降，可以利用稳定因子进行正则化因子自适应调整，

2.3 修正“L-curve”方法

正则化因子α是数据目标函数和模型约束函数的加权系数，是反演的关键参数之一。HANSEN[43]提出用“L-curve”(见图2(a))来确定正则化因子，该方法通过求取双对数坐标下φd(m)与φm( m)曲线最大曲率κ来确定正则化因子α。双对数坐标下φd(m)与φm( m)曲线曲率可表示为

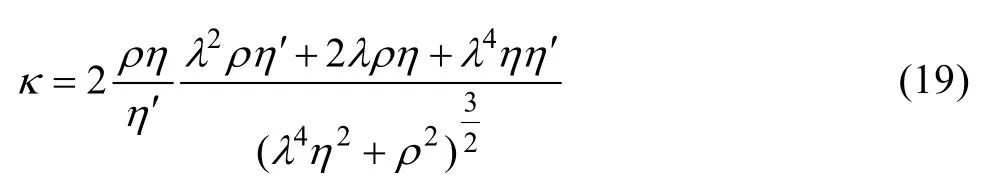
式中：ρ=φd(m)、η= φm(m)；η′为η对α的一阶导数。在反演过程中，由于η是离散的，其导数只能通过数值方法计算，精度不高，严重影响了κ值。另外，在实际试算中发现双对数坐标下φd(m)与φm(m)曲线并不总是呈“L”形，很多情况下表现为两个拐点(见图 2(b))。

针对上述情况，提出了“L-curve”的改进算法，其基本原理是基于点与直线的关系，利用点到直线的距离进行计算，算法具体步骤：

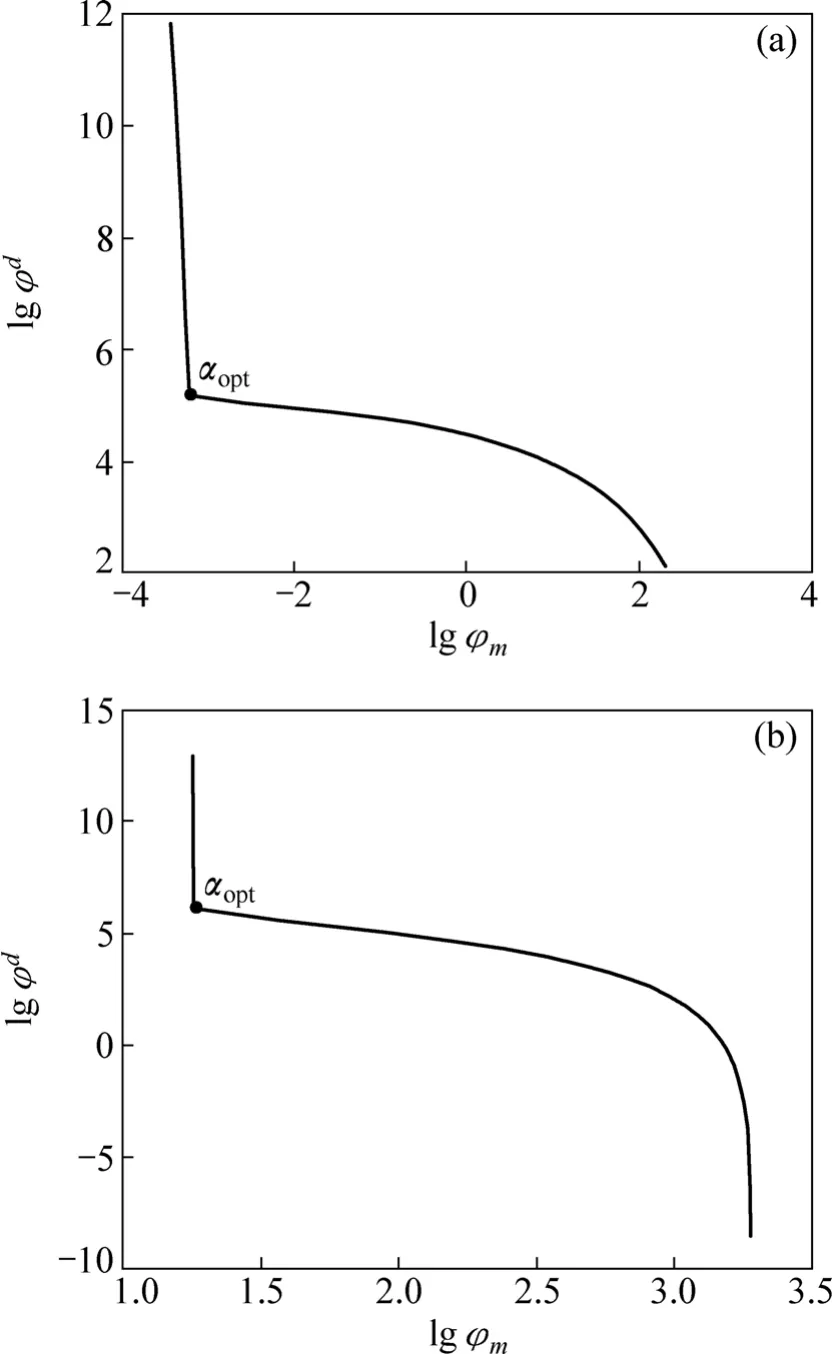
图2 L-Curve特征图Fig.2 L-curve feature map:(a)One inflection point;(b)Two inflection points

1)给出初始的正则化因子{αi}，求解式(9)得到{mαi}， 并 计 算 对 应 的 {( pi,qi)=(lgφd(mαi),lgφm( mαi))}；

2)令 βi=lg αi，对{(βi,pi)}和{(βi,qi)}分别作3次样条插值，分别将插值函数记为p(β)和q(β)；

3)取“L-curve”上的两个端点，计算直线表达式M(Ax+ B y+C=0)；

4)取“L-curve”上的任意点 ( pk,qk)，将其带入直线表达式M中，计算{(pk+Bqk+C＜0}；

5)计算所有 ( pk,qk)到直线M的距离{dk}，筛选出距离最大的点dh；

6)在区间 (αh-1, αh+1)加密剖分，作为初始值重新计算步骤1)～步骤5)，直到满足收敛条件。

改进的“L曲线”算法，无需利用 φm( m)的导数信息，可以自动舍弃错误曲率点，提高了正则化因子的求取精度。

3 反演算例分析

3.1 模型试算

均匀半空间中存在一个倒“L”型的低阻异常体(见图3)，低阻异常体的电阻率为50 Ω·m，背景电阻率为100 Ω·m，在水平坐标10 m与20 m布设井中电极(共32个，每口井16个)，地表布设30个电极。反演数据由模型正演结果加入2%随机噪声得到。分别采用最小梯度支撑、最平滑模型及最小模型稳定因子进行反演，反演断面如图4所示。各种稳定因子均能反映低阻异常体的存在，最小梯度稳定因子得到的反演结果相对其它稳定因子，边界更明显，并且背景电阻率接近100 Ω·m；其它两种稳定因子，反演断面存在多处假异常，异常体边界的陡变程度受到井位置的影响，离井越近边界越明显。

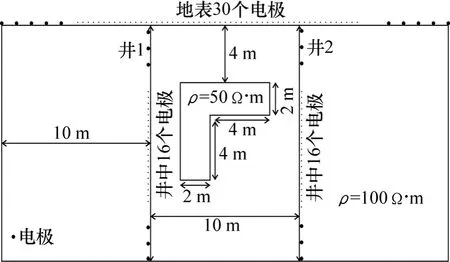
图3 模型示意图Fig.3 Schematic diagram of model

图4 反演电阻率断面Fig.4 Inversion resistivity sections:(a)Minimum gradient support;(b)Maximum smoothness;(c)Minimum norm

3.2 某汉代墓葬区主剖面反演

文物保护单位对某汉代墓葬区进行保护性挖掘，为确定墓室、陪葬坑、墓道的位置及是否存在古代盗洞等情况，进行了直流电法勘探工作。在主剖面探测过程中，利用一个垂向盗洞开展了井地电法测量，地表采用2.5 m极距，共布置60个电极；盗洞中采用1.0 m极距，共布置井中电极8个(电极位置见图5，其中部分在反演区外的地表电极未画出)。采用最小梯度稳定因子的正则化反演目标函数，应用RRCG方法进行了反演，反演电阻率断面如图5所示。

从地表地形推断，两处高程最高的地方(水平坐标20～32 m，55～75 m)为主墓与陪葬墓的封土区，其下方应当存在墓室。两个封土堆的正上方均存在垂向盗洞，其中，右侧年代较久，根据当地百姓反映可能发生在20世纪80年代，左侧盗洞正在开挖还没有达到墓室，左侧盗洞也是利用布置井中电极的盗洞。由反演电阻率断面(见图5)可知，该断面电阻率变化范围为40～400 Ω·m，其中高电阻率区(＞280 Ω·m)主要分布在高程较高和地形变化大的位置，推测主要是由于这些区域有利于排水比较干燥而造成；-10 m以下为低电阻率区(＜100 Ω·m)，结合水文地质资料推测，与地下潜水面有关；右侧封土下在160～220 Ω·m的包围区内存在220～280 Ω·m的封闭异常，推测中间封闭异常为墓室，墓室周围的高阻推测与夯土等施工有关；左侧封土下在 100～160 Ω·m 的包围区内存在 40～100 Ω·m 的封闭异常，推测中间低阻封闭异常为墓室。左、右两侧墓室分别表现为低阻与中高阻，后经现场考查发现，左侧盗洞内部有水，而右侧盗洞内部较为干燥。

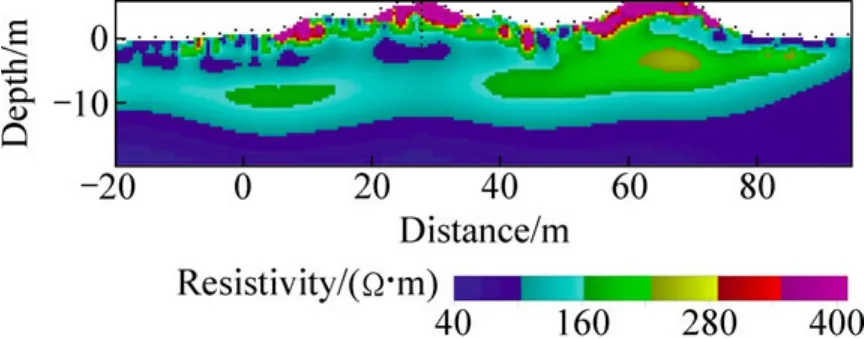
图5 主剖面反演电阻率断面Fig.5 Inversion resistivity section of mainly survey line

4 结论

1)近似的边界处理以及基于符号分析的LDLT分解算法有利于提高了正演计算效率，为快速反演奠定基础。

2)采用改进的“L-curve”求取正则化因子，计算方便，无需对离散数据求导，提高了反演的稳定性。

3)重加权共轭梯度方法通过在每次迭代过程中，计算变权重矩阵eWˆ，并且利用前一次稳定因子与本次稳定因子的比值作为正则化因子的衰减系数，这种迭代过程中自适应求取正则化因子的方法提高了反演效率及结果的稳定性。

4)最小梯度支撑稳定因子有利于提高2.5D井地反演陡变异常体边界的识辨能力。

[1] SMITH N C,VOZOOFF K.Two-dimensional DC resistivity inversion for dipole-dipole data[J]. IEEE Transactions Geoscience Remote Sensing,1984,22(1):21-28.

[2] ZHOU B,GREENHALGH S A.A synthetic study on cross-hole resistivity imaging with different electrode arrays[J].Exploration Geophysics,1997,28(2):1-5.

[3] ZHANG J,MACKIE R L,MADDEN T R.3-D resistivity forward modeling and inversion using conjugate gradients[J].Geophysics,1995,60(5):1313-1325.

[4] OLDENBURG D W,MCGILLICRAY P R,ELLIS R G.Generalized subspace methods for large-scale inverse problem[J].Geophysical Journal International,1993,114(1):12-20.

[5] LI Y G,OLDENBURG D W.Approximate inverse mapping in DC resistivity problems[J].Geophysical Journal International,1992,109(2):343-362.

[6] MAURIELLO P,PATELLA D.Resistivity anomaly imaging by probability tomography[J].Geophysical Prospecting,1999,47(3):411-429.

[7] SCRIBA H.Computation of the electrical potential in the three-dimensional structures[J].Geophysical Prospecting,1981,29(5):790-802.

[8] SPITZER K.3-D finite-difference algorithm for DC resistivity modeling using conjugate methods[J].Geophysical Journal International,1995,123(3):903-914.

[9] PRIDMORE D F,HOHMANN G W,WAED S H,SILL W R.An investigation of finite-element modeling for electrical and electrical and electromagnetic data in three dimensions[J].Geophysics,1981,46(7):1009-1015.

[10]徐凯军,李桐林.垂直有限线源三维地电场有限差分正演研究[J].吉林大学学报(地球科学版),2006,36(1):137-141.XU Kai-jun, LI Tong-lin.The forward modeling of three-dimensional geo-electrical field of vertical finite line source by finite difference method[J].Journal of Jilin University(Earth Science Edition),2006,36(1):137-141.

[11] 王志刚,何展翔,魏文博.井地直流电法三维数值模拟中若干问题研究[J].物探化探计算技术,2006,28(4):322-326.WANG Zhi-gang,HE Zhan-Xiang,WEI Wen-bo.Study on some problems upon 3D modeling of DC borehole-ground method[J].Computing techniques forgeophysicaland Geochemical Exploration,2006,28(4):322-326.

[12] 戴前伟,侯智超,王洪华.井地电位2.5维有限元数值模拟异常分析[J].物探化探计算技术,2013,35(4):457-462.DAI Qian-wei,HOU Zhi-chao,WANG Hong-hua.Anomalous analysis of the 2.5D finite element numerical simulation of borehole-ground electrical method[J].Computing Techniques for Geophysicaland GeochemicalExploration,2013,35(4):457-462.

[13] 柳建新,邓小康,郭荣文,刘海飞,童孝忠,柳 卓.坑道直流聚焦超前探测电阻率法有限元数值模拟[J].中国有色金属学报,2012,22(3):970-975.LIU Jian-xi,DENG Xiao-kang,GUO Rong-wen,LIU Hai-fei,TONG Xiao-zhong,LIU Zhuo.Numericalsimulationof advanced detection with DC focus resistivity in tunnel by finite element method[J].The Chinese Journal of Nonferrous Metals,2012,22(3):970-975.

[14]LI Y G,OLDENBURG D W.3-D inversion of induced polarization data[J].Geophysics,2000,65(6):1931-945.

[15]柯敢攀,黄清华.井地电法的三维正反演研究[J].北京大学学报(自然科学版),2009,45(3):264-272.KE Gan-pan,HUANG Qing-Hua.3D Forward and inversion problems of borehole to surface electrical method[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2009,45(3):264-272.

[16] 吕玉增,阮百尧,黄俊革.直流电井间三维直接成像[J].物探化探计算技术,2003,25(1):60-64.LÜ Yu-zeng,RUAN Bai-yao,HUANG Jun-ge.The 3-D immediate cross hole tomography with directcurrent[J].Computing TechniquesforGeophysicaland Geochemical Exploration,2003,25(1):60-64.

[17] 王志刚,何展翔,魏文博.Born近似快速三维反演井地电法数据[J].地球物理学进展,2007,22(2):508-513.WANG Zhi-gang,HE Zhan-xiang,WEI Wen-bo.Fast 3D inversion of borehole ground electrical method data based on born approximation[J].Progress in Geophysics,2007,22(2):508-513.

[18] 安 然,李桐林,徐凯军.井地三维电阻率反演研究[J].地球物理学进展,2007,22(1):247-249.AN Ran,LI Tong-lin,XU Kai-jun.Well-surface 3-D resistivity inversion[J].Progress in Geophysics,2007,22(1):247-249.

[19]CONSTABLE S C,PARKER R L,CONSTABLE C G.Occam’s inversion:A practical algorithm for generating smooth models from EM sounding data[J].Geophysics,1987,52(3):289-300.

[20]SMITH J T,BOOKER J R.Rapid inversion of two-and three-dimensional magnetotelluric data[J]. Journal of Geophysical Research:Solid Earth,1991,96(3):3905-3922.

[21]ZHDANOV M S. Geophysical inverse theory and regularization[M].New York:Elsevier Science,2002:149-165.

[22]ZHDANOV M S,FANG S.3-D quasi-liner electromagnetic inversion[J].Radio Science,1996,4(3):741-745.

[23]DEGROOT-HEDLIN C,CONSTABLE S.Occam’s inversion to generate smooth,two dimensional models from magnetotelluric data[J].Geophysics,1990,55(12):1613-1624.

[24]RUDIN L I,OSHER S,FATEMI E.Nonlinear total variation based noise removal algorithms[J].Physical D:Nonlinear Phenomena,1992,60(14):259-268.

[25]GAO H,ZHAO H K.Multilevel bioluminescence tomography based on radioactive transfer equation Part 2:Total variation and l1 data fidelity[J].Optics Express，2010,18(3):2894-2912.

[26]BURSTEDDE C,GHATTAS O.Algorithmic strategies for full wave-form inversion:1D experiments[J].Geophysics,2009,74(6):37-46.

[27]韩 波,窦以鑫,丁 亮.电阻率成像的混合正则化反演算法[J].地球物理学报,2012,55(3):970-980.HAN Bo,DOU Yi-xin,DING Liang.Electrical resistivity tomography by using a hybrid regularization[J].Chinese Journal of Geophysics,2012,55(3):970-980.

[28]LAST B J,KUBIK K.Compact gravity inversion[J].Geophysics,1983,48(6):713-721.

[29]GUILLEN A,MENICHETTI V.Gravity and magnetic inversion with minimization of a specific functional[J].Geophysics,1984,49(8):1354-1360.

[30]BARBOSA V C F,SILVA J B C.Generalized compact gravity inversion[J].Geophysics,1994,59(1):57-68.

[31]CANDANSAYAR M E.Two-dimensionalinversion of magnetotelluric data with CG and SVD:A comparison study of differentstabilizers[J].SEG TechnicalProgram Expanded Abstracts,2002,21(1):669-672.

[32]MEHANEE S, ZHDANOV M S. Two-dimensional magnetoelluric inversion of blocky geo-electrical structures[J].Journal of Geophysical Research,2002,107(B4):2065-2075.

[33]PORTNIAGUINE O,ZHDANOV M S.3-D magnetic inversion with data compression and image focusing[J].Geophysics,2002,67(5):1532-1541.

[34]GRIBENKO A,ZHDANOV M.Rigorous 3-D inversion of marine CSEM data based on the integral equation method[J].Geophysics,2006,25(1):815-819.

[35]VIGNOLI G,DEIANA R,CASSIANI G.Focused inversion of vertical radar profile(VRP)travel time data[J].Geophysics,2012,77(1):9-18.

[36]PORTNIAGUINE O,ZHDANOV M S.Focusing geophysical inversion images[J].Geophysics,1999,64(3):874-887.

[37]ZHDANOV M S,ELLIS R,MUKERJEE S.Three-dimensional regularized focusing inversion of gravity gradient tensor data[J].Geophysics,2004,69(4):925-937.

[38]SALAH A M. Multidimensional finite difference electromagnetic modeling and inversion based on the balance method[D].Utah:The University of Utah,2003.

[39] 刘小军,王家林,陈 冰,于 鹏.二维大地电磁数据的聚焦反演算法探讨[J].石油地球物理勘探,2007,42(3):338-342.LIU Xiao-jun,WANG Jia-lin,CHEN Bing,YU Peng.The focusing inversion of 2-D magnetotelluric[J].Oil Geophysical Prospecting,2007,42(3):338-342.

[40]徐世浙.地球物理中的有限单元法[M].北京:科学出版社,1994:159-178.XU Shi-zhe.The Finite element method in Geophysics[M].Beijing:Science Press,1994:159-178.

[41]ERHAN E,ISMAILD,MEHMETE C.Incorporating topography into 2D resistivity modeling using finite-element and finite-difference approaches[J]. Geophysics, 2008, 73(3):135-142.

[42] LIU J.The role of elimination trees in sparse factorization[J].SIAM Journal on Matrix Analysis and Applications,1990,11(1):134-172.

[43]HANSEN P C.Analysis of discrete ill-posed problems by means of the L-curve[J].Siam Review,1992,34(4):561-580.