5052铝合金冲压成形过程中韧性断裂的仿真研究

余海燕，王 友

(同济大学 汽车学院，上海 201804)

铝合金由于具有密度低、耐腐蚀高、比强度高等特点，近来作为重要的轻质材料在汽车制造中被广泛使用[1-3]。破裂、起皱和回弹是板料冲压成形中的三大主要质量缺陷。铝合金和钢板相比，总伸长率更小，在室温下铝合金的成形性比钢板的差，更容易出现破裂现象[4-6]。准确模拟板料成形过程中的破裂现象，对成形工艺和模具设计具有重要意义。

金属材料的断裂主要可以分为脆性断裂和韧性断裂，多数铝合金属于韧性断裂[7-8]。韧性断裂准则从细观损伤力学角度出发，认为材料内部孔洞的缺陷在外力作用下不断地形核、长大并聚合, 最终引起了材料的损伤，可以较好地预测塑性差的板料成形性能[9-10]。

影响韧性断裂的因素很多，主要可以分为两大类。一类与材料相关[11]，如应变硬化水平、空穴体积分数和第二相粒子组成等；第二类与工艺相关[12-14]，如应变速率、摩擦和成形温度等。韧性断裂是制约金属成形的一个重要因素，因此，很多学者以损伤思想为背景，提出了韧性断裂准则。

LEMAITRE[15]基于热力学提出塑性损伤模型：

式中：εR和εD分别为材料单向拉伸损伤应变与损伤应变门槛值；σm是平均应力；是等效应力；ν是泊松比；p是塑性应变累积；Dc是临界损伤值；D为材料常数。OYANE等[16]研究多孔体材料在压缩状态下的本构关系，考虑平均应力的影响提出如下韧性断裂准则：

COCKCROFT等[17]认为对于某些给定的材料，最大拉应力是导致破坏的主要因素，当单位体积的塑性功达到某一极限值时材料发生破坏。将最大拉应力沿塑性应变路径积分，得到如下断裂准则：

式中：maxσ为最大拉应力；C为材料常数。

于忠奇等[18]针对塑性差的材料在破裂前无颈缩的现象，提出如下断裂准则：

式中：p和C均为材料常数。

由于有限元计算可获得板料变形过程中单元应力应变分布，因此可方便地将韧性断裂准则引入板料成形仿真，用于预测断裂的发生。CLIFT等[19]对墩粗、双向等拉、单向拉伸和压缩试验进行了预测。研究结果显示，考虑了材料广义塑性功极限值的断裂准则能更准确地预测材料断裂。TAKUDA等[20]将 Oyane准则、Cockcroft-Latham准则、Brozzo准则和Clift准则等用于铝合金和低碳钢板拉深成形的断裂预测中。结果表明，通过Cockcroft-Latham准则、Oyane准则和Brozzo准则均能够得出比较准确的预测。考虑到Cockcroft-Latham韧性断裂准则在铝合金板拉深成形中预测较准确，且材料常数容易确定，因此本研究中球头胀形数值模拟使用该准则作为材料的破裂判据。

本文作者通过标准单向拉伸试验获得 5052铝合金的应力-应变曲线，并通过拟合曲线获得5052铝合金的Voce模型参数，选择合适的韧性断裂准则，结合单向拉伸试验与有限元数值模拟确定 5052铝合金的材料失效参数。将获得的材料参数引入球头胀形数值模拟中，使用LS-DYNA软件预测5052铝合金极限胀形能力，并进行试验验证。

1 单向拉伸试验

试验所用材料为5052防锈铝合金，铝合金板厚度为1 mm。试样依据ASTM E8/E8-09单向拉伸试验标准制备，试样尺寸如图1所示，采用电火花线切割加工。单向拉伸试验在电子万能试验机SANS上进行，为了减少应变速率波动的影响，试验中拉伸速度设置为1 mm/min。

图1 单向拉伸试样尺寸Fig. 1 Dimensions of uniaxial tensile specimen (Unit: mm)

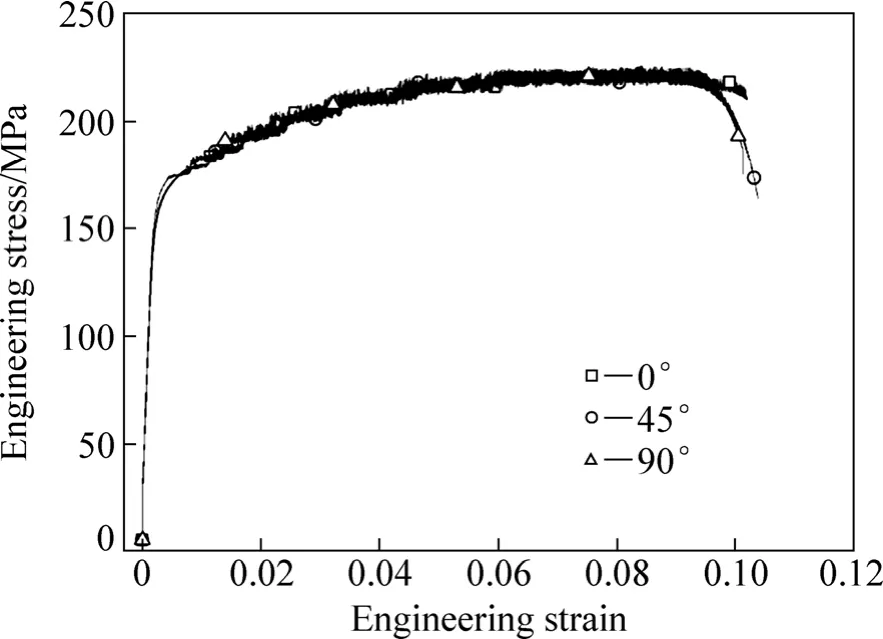
图2 5052铝合金板单向拉伸工程应力-应变曲线Fig. 2 Engineering strain—stress curves of 5052 aluminum alloy sheet in uniaxial tensile tests

5052铝合金的工程应力-应变曲线如图2所示。由图2可以看出，0°、45°和90°这3个方向的拉伸试验曲线非常接近，弹性模量均为60624 MPa；名义屈服强度分别为175 MPa、185 MPa和175 MPa；抗拉强度分别为220 MPa、210 MPa和215 MPa；总伸长率分别为10%、11.2%和10.5%。由试验结果可知，5052铝合金3个方向的弹性模量、屈服强度、抗拉强度和总伸长率都非常接近，这说明5052铝合金各向异性较弱。

图3所示为拉伸断裂后的铝合金试样照片。试样断口与轴向所成角度约为45°，断口平整。使用扫描电子显微镜观察5052铝合金拉伸试样断口的形貌，结果如图4所示。从图4可以看出，5052铝合金拉伸试样断口存在两种类型的韧窝。第一种韧窝的外形大而深，说明5052铝合金属于韧性断裂；第二种韧窝外形较小，在韧窝的底部和四周分布着一定量的球形颗粒，说明5052铝合金有部分脆性断裂。由于第二种韧窝比例较少，因此5052铝合金的主要断裂机制属于韧性断裂。

图3 拉伸断裂后铝合金试样照片Fig. 3 Photo of failed aluminum alloy tensile specimen

图4 单向拉伸试样断口的SEM像Fig. 4 SEM image of fracture surface of tensile specimen

表1 5052铝合金的材料参数Table 1 Material parameters of 5052 aluminum alloy

2 材料参数识别

使用LS-DYNA有限元软件分别对单向拉伸和球头胀形进行仿真。材料模型选择MAT_135，该模型能够使用Voce非线性各向同性硬化模型，以及将材料的断裂应变能作为失效判据。由于5052铝合金表现出来的各向异性较弱，因此，MAT_135对其具有较好的适用性。仿真中使用的材料本构模型由Barlat89屈服准则，Voce模型和流动方程[21]结合而来。采用Cockcroft-Latham韧性断裂准则进行断裂预测。

2.1 Voce硬化模型参数拟合

根据文献[22]，Voce模型的各参数可以通过拟合材料应力-应变曲线得到，使用Voce模型对 5052铝合金的应力-应变曲线进行拟合，拟合所得曲线和材料参数分别见图 5和表 1，其中 Q1、Q2、C1、C2为Voce模型的材料参数。拟合曲线和试验曲线的相关系数为0.995，拟合相似度较高。

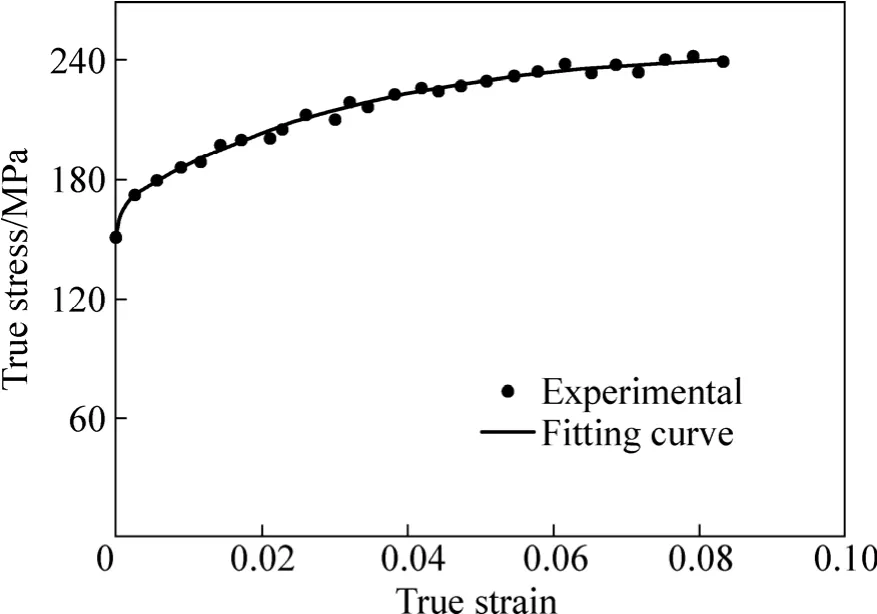
图5 试验和拟合所得5052铝合金的应变硬化曲线Fig. 5 Experimental and fitting strain-hardening curves of 5052 aluminum alloy

图6所示为单向拉伸试样有限元模型，网格平均尺寸为1 mm。厚度方向采用5个积分点，使用16号全积分壳单元。试样的一端添加固定约束，另一端以1 mm/min的恒定速度沿轴向运动。材料使用MAT_135模型，硬化模型选择Voce非线性各向同性硬化模型，采用如表1所列的拟合得到的Voce模型参数，材料的泊松比和各向异性指数由材料供货方提供。使用LS-DYNA的隐式模块进行求解。

在仿真过程中，单向拉伸试样随着变形增加先后会出现均匀变形和局部颈缩。由于仿真模型中缺少材料失效判据，所以当拉伸位移不断增加时，试样的厚度会持续减薄直至为 0，但是不会出现直观断裂。试样在拉伸仿真中厚度分布云图变化如图7所示。由图7可知，随着试样变形的增加，试样厚度不断减薄，中间区域厚度减薄得最快。在初始时刻，试样标距区域变形均匀，随着拉伸位移的增加，试样变形不断增大，试样中部宽度出现明显变窄，即局部颈缩。

图 8所示为仿真与试验获得的应力-应变曲线对比结果。由图8可以看到，在试样发生颈缩之前仿真和试验结果吻合较好。一方面，说明采用拟合所得Voce模型参数描述材料断裂之前的应力应变行为有较高的精度。另一方面，在有限元数值模拟中由于没有添加断裂失效判据，所以单元的拉应力在出现颈缩之后依然会随着拉伸位移的增大而继续变大，与实际应力-应变曲线出现不同趋势走向。因此，以下将对断裂准则中的参数进行反求，以更准确地模拟材料弹塑性直至断裂整个变形过程的力学行为。

图6 单向拉伸试样有限元模型Fig. 6 FE model of uniaxial tensile specimen

图7 单向拉伸试样厚度分布云图Fig. 7 Thickness distribution contours of uniaxial tensile specimen: (a) t=10.4 s; (b) t=35.7 s; (c) t=82.3 s

图8 仿真和试验所得的拉伸应力-应变曲线Fig. 8 True stress-strain curve from tensile simulation and experiment

图9 单向拉伸仿真中试样最小厚度的变化曲线Fig. 9 Changing curve of minimum thickness of specimen in numerical uniaxial tensile test

图10 最大应变能随等效塑性应变的变化曲线Fig. 10 Changing curve of maximum strain energy with equivalent strain

2.2 Cockcroft-Latham断裂准则参数反求

根据Cockcroft-Latham韧性断裂准则，材料单元的断裂应变能等于试样单元中最大拉应力沿塑性应变路径的积分。本实验中使用模型中最大拉应力对最大等效塑性应变进行积分，得到材料的断裂应变能。

单向拉伸仿真中试样最小厚度随时间的变化曲线如图9所示。将不同时刻单元最大拉应力对塑性应变积分得到单元最大应变能，作出单元最大应变能随塑性应变变化的曲线如图 10所示。使用光学显微镜测量拉伸断裂试样断口的最小厚度值为0.42 mm，从图9中读出仿真中试样达到实测最小厚度的时刻为58 s，该时刻即为试样发生韧性断裂时刻。在仿真结果中查到58 s时模型中最大等效塑性应变为0.458，由图10可知，此时模型中单元最大应变能为109 MPa，此单元应变能即为5052铝合金的断裂应变能。5052铝合金材料的失效模型参数如表2所示。

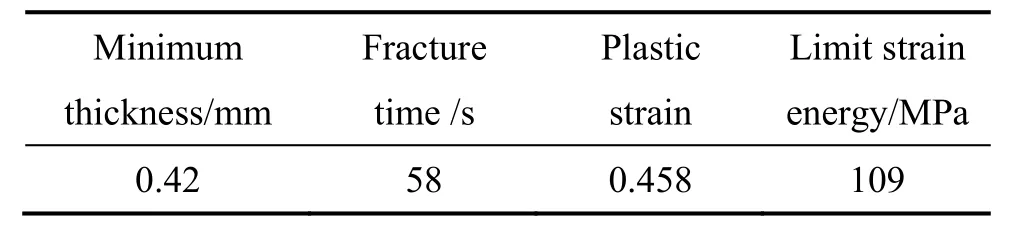
表2 5052铝合金的失效模型参数Table 2 Parameters of fracture model of 5052 aluminum alloy

3 球头胀形仿真与试验

球头胀形模具尺寸如图11所示，凸模直径为100 mm，模具单边间隙为2 mm，拉延筋半径为5 mm，凹模圆角半径为5 mm。毛坯为180 mm×180 mm的5052铝合金方形板料，厚度为1 mm。在板料中部直径为100 mm圆形区域内使用平均尺寸为0.8 mm的四边形网格进行划分，其他区域使用平均尺寸为 5 mm的四边形和三角形混合网格划分。采用16号全积分

壳单元，厚度方向采用 5个积分点。接触类型选择FORMING_ ONE_WAY_S_S，摩擦因数设为0.125。冲压速度为 1mm/s，冲压深度 25mm。参考冲压手册[23]，选择单位压边力为0.85 MPa，根据压边圈尺寸选取压边力为20 kN。材料模型选择MAT_135模型，使用2.1和2.2节中获得的Voce模型参数和断裂应变能。球头胀形数值模拟中不同时刻板料的外形如图12所示。

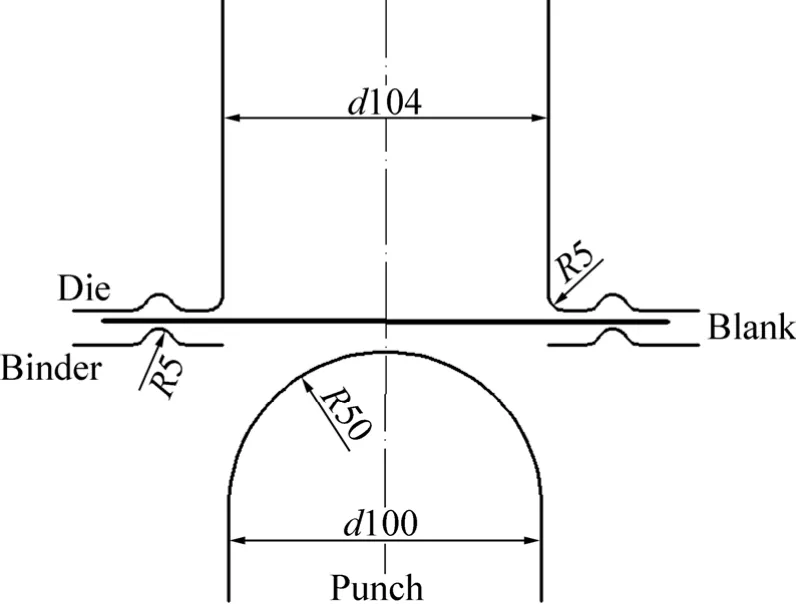
图11 球头胀形模具尺寸Fig. 11 Dimensions of spherical bulging moulds (Unit: mm)

图12 球头胀形过程中不同时刻板料外形Fig. 12 Shapes of sheet in spherical bulging at different time: (a) t=8.8 s, h=8.8 mm; (b) t=18.2 s, h=18.2 mm; (c) t=22.3 s, h=22.3 mm; (d) t=25 s, h=25 mm

板料在成形过程中单元的应变能会随着变形的增加而增加，当单元的应变能(W)达到材料的断裂应变能(Wc)时单元失效。LS-DYNA模拟成形仿真时会自动删除失效单元并且释放周围节点的自由度，以此模拟成形过程中裂纹的扩展。从图12可以看到，球头顶部侧围减薄最多(见图12(a)中蓝色圆环区域)。随着冲压深度的增加，在球头的侧围出现一条平行于水平面的裂纹(见图12(b))。当冲压深度达到22.3 mm时，在水平面内垂直于第一条裂纹方向出现第二条裂纹，同时第一条裂纹扩大(见图12(c))。当凸模行程增加至25 mm时，两条裂纹同时扩大，并形成一个巨大的缺口(见图12(d))。

球头胀形试验在天锻THP01-500A型多功能冲压成形模拟机试验上完成。试验所用模具尺寸、试样尺寸和冲压工艺参数均与仿真模型相同，试验过程中采取双面润滑。在试验过程中不断调整冲压深度直至板料出现破裂；当冲压深度为25 mm时，板料出现破裂，如图13所示。

图13 板料球头胀形破裂Fig. 13 Cracked sheet in spherical bulging experiment

从图13可以看到，板料在成形至断裂的过程中出现了明显的颈缩，宏观断口表现为沿着与厚度方向成45°方向断裂，开裂部位断口比较平整，没有出现不规则的起伏，板料厚度在刃口附近出现了明显的减薄。

图14所示为板料球头胀形仿真与试验结果对比。从图 14可以看到，有限元仿真结果与试验结果较吻合，板料开裂处裂纹的位置和形状大小与试验结果接近。说明有限元仿真分析具有较高的模拟精度以及上述获得的Voce模型参数Q1、C1、Q2、C2和断裂应变能Wc是合理的，Cockcroft-Latham韧性断裂准则能够很好地预测5052铝合金板料成形的开裂失效。

图14 板料球头胀形仿真与试验结果对比Fig. 14 Comparison of sheet deformation results in spherical bulging: (a) Simulation; (b) Experiment

4 结论

1) 对5052铝合金板进行了单向拉伸试验，使用Voce模型对试验应力应变曲线进行了拟合。将Cockcroft-Latham韧性断裂准则引入到单向拉伸有限元模型中，结合试验结果，反求了5052铝合金材料失效参数。

2) 采用拟合的 Voce模型参数和 Cockcroft-Latham韧性断裂准则参数对5052铝合金板料球头胀形开裂进行了仿真预测，并进行试验验证，结果表明仿真预测板料开裂位置及裂口形状与试验结果吻合。

3) 使用该方法进行铝合金板料的成形开裂极限预测具有材料参数求解方便，计算精度高的优点，可为相关研究提供参考。

[1] 叶延洪, 何 静, 蔡建鹏, 孙加民, 邓德安. 6061-T651铝合金薄板接头的焊接变形[J]. 中国有色金属学报, 2014, 24(10):2435-2442.YE Yan-hong, HE Jing, CAI Jian-peng, SUN Jia-min, DENG De-an. Welding deformations of 6061-T651 Al alloy thin-plate joints[J]. The Chinese Journal of Nonferrous Metals, 2014,24(10): 2435-2442.

[2] THUILLIER S. Influence of a tensile pre-strain on bending of aluminium alloy[C]//Key Engineering Materials. Switzerland:Trans Tech Publications, 2014, 611: 1742-1749.

[3] 马闻宇, 王宝雨, 周 靖, 唐学峰. AA6082铝合金热变形损伤本构模型[J]. 中国有色金属学报, 2015, 25(3): 595-601.MA Wen-yu, WANG Bao-yu, ZHOU Jing, TANG Xue-feng.Damage constitutive model for Thermal deformation of AA6082 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals,2015, 25(3): 595-601.

[4] ZHU H, QI F. Mechanical properties and fracture behaviors on 6061 aluminum alloy under shear stress state[J]. Rare Metals,2011, 30(5): 550-554.

[5] FAGERHOLT E, DØRUM C, BØRVIK T, LAUKLI H.Experimental and numerical investigation of fracture in a cast aluminium alloy[J]. International Journal of Solids and Structures, 2010, 47(24): 3352-3365.

[6] HIRSCH J. Recent development in aluminium for automotive applications[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(7): 1995-2002.

[7] 叶 拓, 王 冠, 姚再起, 李落星. 汽车用 6xxx系铝合金薄壁件的韧性断裂行为[J]. 中国有色金属学报, 2014, 24(4):878-887.YE Tuo, WANG Guan, YAO Zai-qi, LI Luo-xing. Ductile fracture behavior of 6xxx aluminum alloy thin-walled components of automobile[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(4): 878-887.

[8] 刘 超, 孙 秦, 刘彦杰. 三维应力状态下2A12试件有限变形和断裂的数值模拟[J]. 中国有色金属学报, 2014, 24(5):1157-1166.LIU Chao, SUN Qin, LIU Yan-jie. Numerical simulation of finite deformation and failure of 2A12 specimens under three-dimensional stress state[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(5): 1157-1166.

[9] 谢延敏, 于沪平, 陈 军, 阮雪榆. 板料成形中韧性断裂准则应用研究进展[J]. 工程设计学报, 2007, 14(1): 6-10.XIE Yan-min, YU Hu-ping, CHEN Jun, RUAN Xue-yu. Recent advances of research on application of ductile fracture criteria in sheet metal forming process[J]. Chinese journal of Engineering Design, 2007, 14(1): 6-10.

[10] XING H U, ZHAO Y X, LI S H, LIN Z Q. Numerical simulation of ductile fracture behavior for aluminum alloy sheet under cyclic plastic deformation[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(7): 1595-1601.

[11] OLOFSSON J, SVENSSON I L, LAVA P, DEBRUYNE D.Characterization and investigation of local variations in mechanical behaviour in cast aluminium using gradient solidification, digital image correlation and finite element simulation[J]. Materials & Design, 2014, 56: 755-762.

[12] FOURMEAU M, BØRVIK T, BENALLAL A, HOPPERSTAD O S. Anisotropic failure modes of high-strength aluminium alloy under various stress states[J]. International Journal of Plasticity,2013, 48: 34-53.

[13] EBNOETHER F, MOHR D. Predicting ductile fracture of low carbon steel sheets: Stress-based versus mixed stress/strain-based Mohr-Coulomb model[J]. International Journal of Solids and Structures, 2013, 50(7): 1055-1066.

[14] LE MAOÛT N, THUILLIER S, MANACH P Y. Aluminum alloy damage evolution for different strain paths-application to hemming process[J]. Engineering Fracture Mechanics, 2009,76(9): 1202-1214.

[15] LEMAITRE J. A continuous damage mechanics model for ductile fracture[J]. Journal of Engineering Materials and Technology, 1985, 107(1): 83-89.

[16] OYANE M, SATO T, OKIMOTO K, SHIMA S. Criteria for ductile fracture and their applications[J]. Journal of Mechanical Working Technology, 1980, 4: 65-81.

[17] COCKCROFT M G, LATHAM D J. Ductility and the workability of metals[J]. Journal of the Institute of Metals, 1968,96: 33-39.

[18] 于忠奇, 杨玉英, 王永志, 孙振忠. 基于韧性断裂准则的铝合金板材成形极限预测[J]. 中国有色金属学报, 2003, 13(5):1223-1226.YU Zhong-qi, YANG Yu-ying, WANG Yong-zhi, SUN Zhen-zhong. Application of ductile fracture criterion to prediction of forming limit in aluminum alloy sheet forming[J].The Chinese Journal of Nonferrous Metals, 2003, 13(5):1223-1226.

[19] CLIFT S E, HARTLEY P, STURGESS C E N, ROWE G W.Fracture prediction in plastic deformation processes[J].International Journal of Mechanical Sciences, 1990, 32: 1-17.

[20] TAKUDA H, MORIK, HATTA N. Application of some criteria for ductile fracture to the prediction of the forming limit of sheet metals[J]. Journal of Materials Processing Technology, 1999,95(1/3): 116-121.

[21] REYES A, HOPPERSTAD O S, LADEMO O G, LANGSETH M. Modeling of textured aluminum alloys used in a bumper system: Material tests and Characterization[J]. Computational Materials Science, 2006, 37(3): 246-268.

[22] TARIGOPULA V, HOPPERSTAD O S, LANGSETH M,CLAUSEN A H, HILD F, LADEMO O G, ERIKSSON M. A study of large plastic deformations in dual phase steel using digital image correlation and FE analysis[J]. Experimental Mechanics, 2008, 48(2):181-196.

[23] 王孝培. 冲压手册[M]. 2版. 北京: 机械工业出版社, 2000:309-311.WANG Xiao-pei. Stamping manual[M]. 2nd ed. Beijing: China Machine Press, 2000: 309-311.