大跨径悬索桥施工猫道气动力系数数值分析

李胜利，胡亚楠，杜道倾，王东炜

(郑州大学 土木工程学院，河南 郑州450001)

0 引言

猫道是大跨度柔性透风索结构且刚度小，对风敏感．猫道在风荷载作用下，若产生较大变位将会影响主缆的施工安全甚至成桥后主缆的受力［1-3］．为了加快施工进度，降低费用，保证正常的通航要求，国内外均开始使用不设抗风缆的猫道，这就对该类猫道的抗风安全提出了更高的要求［4-5］．为了确保无抗风缆猫道安全，有必要对其气动力系数进行分析． 在过去相当长的一段时间里，风工程中常假定具有尖锐边角断面的实体(即钝体)周围流场不依赖于雷诺数的变化［6］．实践表明，在钝体断面的桥梁结构流场中存在雷诺数效应［7］随着悬索桥跨度越来越大，猫道也向大跨、轻质方向发展，雷诺数对猫道断面气动力系数的影响日渐突出，忽略其影响会给猫道抗风设计带来危险［8-10］．因此，研究雷诺数对猫道断面气动力系数的影响显得非常必要，随着计算机技术和计算流体力学方法的迅速发展，CFD 数值模拟方法已经成为研究猫道断面气动力系数的新手段，该方法不仅可以按照实际尺寸进行计算，而且费用少、速度快、资料完备，同时，还具有模拟真实和理想条件的能力［11］．笔者以某大跨径悬索桥猫道断面气动力系数为研究对象，利用计算流体力学软件Fluent，通过采用3 种不同湍流模型，即标准k-ε 模型、RNG k-ε 模型和SST 模型，对猫道断面的气动力系数在不同风速、不同攻角和不同雷诺数情况下进行CFD 方法识别，与节段模型风洞试验的试验值进行对比分析．

1 猫道气动力系数模拟参数确定

1．1 工程概况

图1 ～3 为某大跨径悬索桥猫道的平面图、横断面图和侧面图． 西南交通大学风工程试验研究中心对该猫道进行了节段模型静力试验，试验风速为:v=10，20，30 m/s;试验攻角为:α = -5° ～+5°，节段模型采用1∶6 的几何缩尺比，其模型长L=2．100 m，宽B=0．692 7 m，高H=0．241 7 m，长宽比L/B=3．03［12］．本研究采用数值模拟的参数设置方法，CFD 模型所采用的尺寸、比例、风速、攻角和风洞试验相同，计算采用风轴坐标系，其定义如图4 所示．

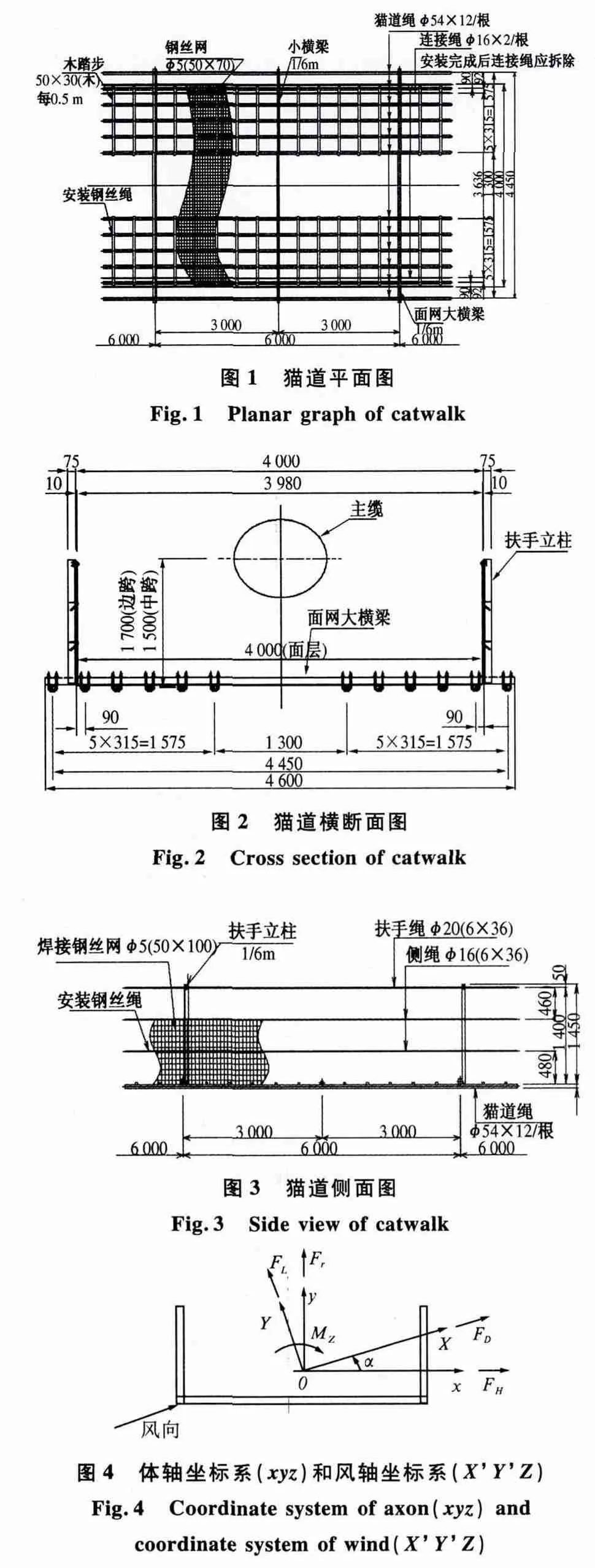
1．2 计算参数的设置

本研究采用Gambit 软件建立数值模型．由于风洞试验一般要求测出气动力系数在-5° ～5°区间的变化曲线，因此通过数值模拟得到猫道断面风攻角在-5° ～5°范围内的气动力系数是合理的、可行的．猫道断面用横向单排直径为4 mm 和竖向单排直径为2 mm 的圆来模拟，模拟透风率分别为84．09%和85．6%，猫道实际透风率分别为84．2%和85．5%，模拟值和实际值差别很小．模型缩尺比取1/6，计算域为24 m ×8 m 的矩形区域(如图5 所示)，入口距迎风面的距离取8 m，计算域上下边界距模型的距离分别为3．75 m 和4 m，背风面距出口的距离取15．3 m，这样可以尽量避免物体后部卷起的分离漩涡打到外边界又反射回来，同时也使外边界附近的流场参数分布较好地与所假定的边界条件相容，求解可以达到很好的收敛性［13］． 边界条件:迎风面边界条件定义为速度进口边界条件，空气密度取1．225 kg/m3;背风面边界条件定义为压力出口边界条件，相对压力值取为零;上下边界均为无滑移的墙面;猫道断面外壁定义为无滑移的墙面(如图5 所示)． 由于猫道断面沿纵向基本不变，因此猫道计算模型可近似按二维模型处理，横风向空气的流动处理为二维定常不可压，在计算分析中不考虑温度变化和能量交换，静力计算按定常来处理，流场计算方法选择SIMPLE 算法，离散格式选择二阶迎风格式．同时采用非结构化网格对猫道断面计算域进行网格划分，并对猫道断面壁面处采取加密网格，使数值模拟更接近于实际情况，迭代残差值控制为10-6．因为网格划分的质量好坏直接影响模拟结果的精度，所以在进行计算分析之前，要对网格划分的质量进行评估，对于网格划分质量较差的要进行优化［14］．笔者在划分网格时通过数次优化调节，最终得到较合理的网格划分形式，如图6 所示．

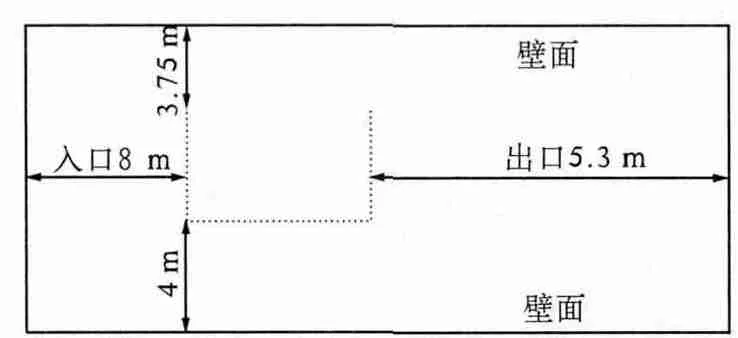
图5 猫道断面计算域Fig．5 Computational domain of catwalk cross section

图6 猫道断面CFD 计算网格Fig．6 The catwalk cross section of CFD computational grid

1．3 湍流模型的选择

目前，在实际工程中被广泛采用的钝体的绕流湍流模式是涡黏性模式即两方程模型里的标准k-ε 模型、RNG k-ε 模型和SST 模型．

标准k-ε 模型是应用最广泛同时也是经验积累最多的湍流模型．其方程形式简单，计算量比较小，也能很好地模拟实际工程的湍流运动，并能取得较好的模拟结果，因此是模拟湍流流动的首选模型［15］．由于标准k-ε 模型假定动黏性系数是各向同性的标量并且在弯曲流线的情况下，湍流流动是各向异性的，从而在模拟强旋流、弯曲流线或弯曲壁面时出现一定的失真． 为了弥补标准k-ε模型的缺陷，许多研究者对标准k-ε 模型进行了修正，RNG k-ε 模型就是其中的一种修正方案．RNG k-ε 模型是标准k-ε 模型的改进方案，与标准k-ε 模型相比，RNG k-ε 模型修正了湍流的黏度和在ε 方程中增加了反映流体的时均应变率项．为了弥补标准k-ε 模型对湍流模拟的缺陷，Mente 通过混合函数将二者结合起来而产生的SST 模型，既可以在靠近壁面的区域采用k-ω 湍流模型，又可以在边界层边缘以及自由剪切层采用k-ω 形式的k-ε 模型并且过渡区域可以通过混合函数来过渡［16］，所以SST 模型集结了标准k-ε湍流模型和k-ω 湍流模型的优点［17］．为了比较选择合适的猫道数值模拟湍流模型，笔者进行了3种湍流模型的计算．

1．4 气动力系数的定义

对于阻力系数来说，由图7 可见，在-5° ～0°攻角范围内，SST 湍流模型的模拟值和试验值非常接近，但试验值比模拟值略大;在0° ～5°攻角范围内，标准k-ε 湍流模型的模拟值均比试验值大;-5° ～5°攻角范围内，SST 湍流模型的模拟值变化趋势总体较其他计算模型更符合试验值变化趋势．可见，不同风攻角时，理论模拟值和试验值差别大小不同，但整体上SST 湍流模型的模拟值更接近试验值．

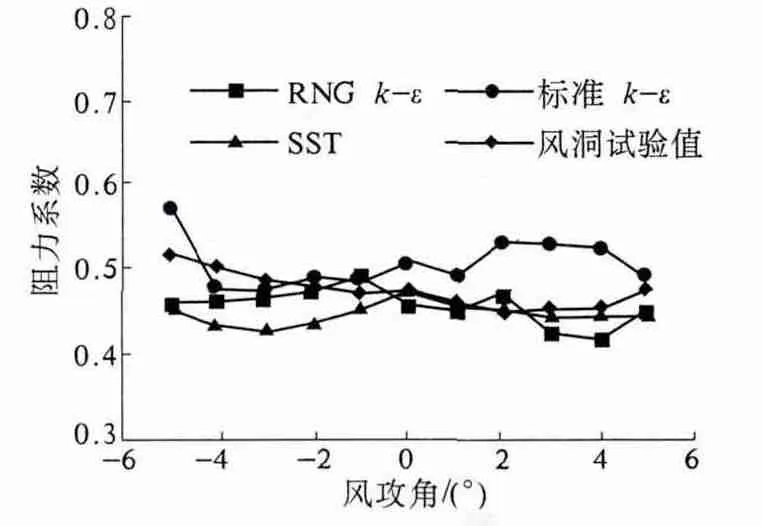
图7 猫道断面阻力系数与风洞试验值对比Fig．7 Compared drag coefficients of the catwalk cross section with results of wind tunnel test

作用在猫道上的静风荷载可分为横向风载(阻力)D，竖向风载(升力)L． 在静风作用下，结构的姿态发生改变，静风与猫道截面的相对攻角随之改变，气动力系数是随攻角变化而改变的，同时平均风速也随着猫道的变形而改变，因此引入有效风攻角和有效风速的概念，将静风荷载表示为有效风速、气动力系数和有效风攻角的函数，具体气动力系数的定义如下

对于升力系数来说，由图8 可见，在所有风攻角范围内，3 种湍流模型的模拟值差别微小． 在-5° ～-3°攻角范围内，标准k-ε 湍流模型和试验值有较大差别;在-5° ～-3°攻角范围内，试验值均比RNG k-ε 和SST 湍流模型模拟值大;在-3° ～5°攻角范围内，试验值与模拟值变化趋势基本相同;整体来说，RNG k-ε 和SST 湍流模型的模拟值与风洞试验值更为接近．

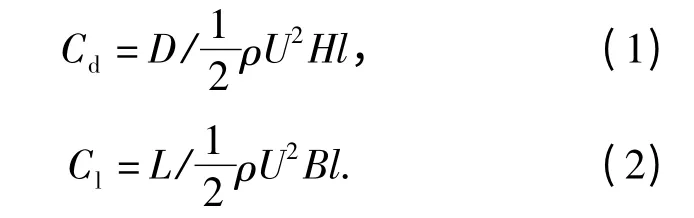
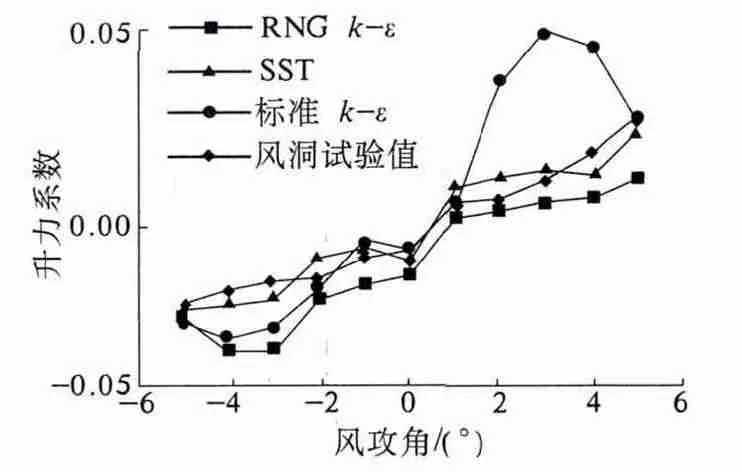
图8 猫道断面升力系数与风洞试验值对比Fig．8 Compared life coefficients of the catwalk cross section with results of wind tunnel test

式中:Cd、Cl分别为阻力系数、升力系数;D，L 分别为风轴坐标系下猫道所受到的气动阻力、升力;ρ为空气密度，取1．225 kg/m3;U 为离断面足够远处来流的平均风速;H 表示节段模型的高度;l 表示节段模型的长度;B 为节段模型宽度．

2 数值模拟与试验结果对比分析

3 种不同湍流模型的数值计算结果与试验结果如图7 和8 所示．

由上述分析可知，在-5° ～5°风攻角范围内，CFD 计算的阻力和升力系数与试验值变化趋势基本一致，并且在阻力系数曲线吻合程度上，SST模型曲线的变化趋势与试验结果趋势基本一致，能较好地反映试验值的变化规律． 虽然3 种模型计算结果与试验值均有一定差距，但是考虑到绝对误差值均较小，因此阻力和升力系数的模拟值和试验值的差别是可以接受的，同时也说明本研究所用猫道透风率的二维模拟方法是可行的．

3 猫道气动力系数的雷诺数效应

由上节的计算结果可知，SST 模型为猫道断面气动力系数CFD 方法识别的最合理的模型．因此笔者采用SST 模型，研究雷诺数Re 变化对不同风攻角下猫道断面气动力系数的影响，雷诺数的设置方法如表1 所示． CFD 模拟计算不同雷诺数对猫道气动力系数的影响结果如图9 和10 所示．

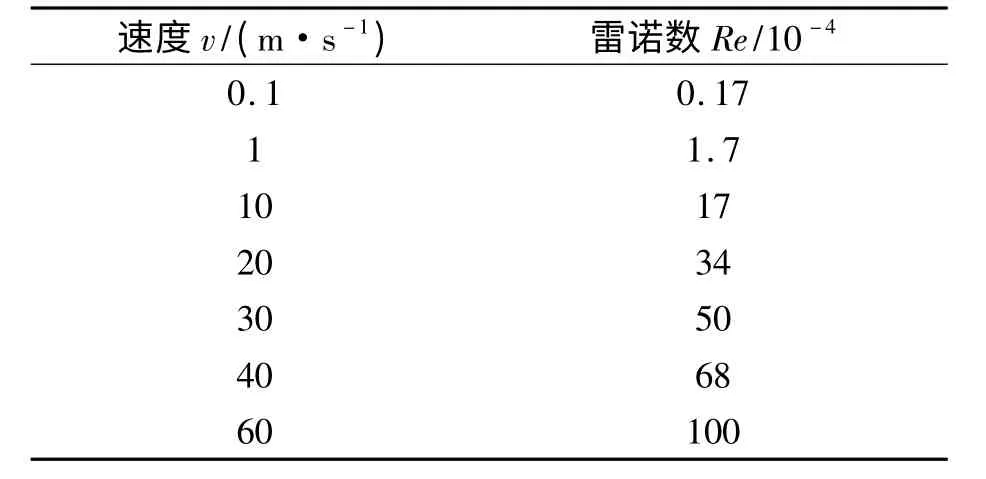
表1 猫道试验断面风速和雷诺数表Tab．1 The table of catwalk test cross section wind speed and reynolds numbers

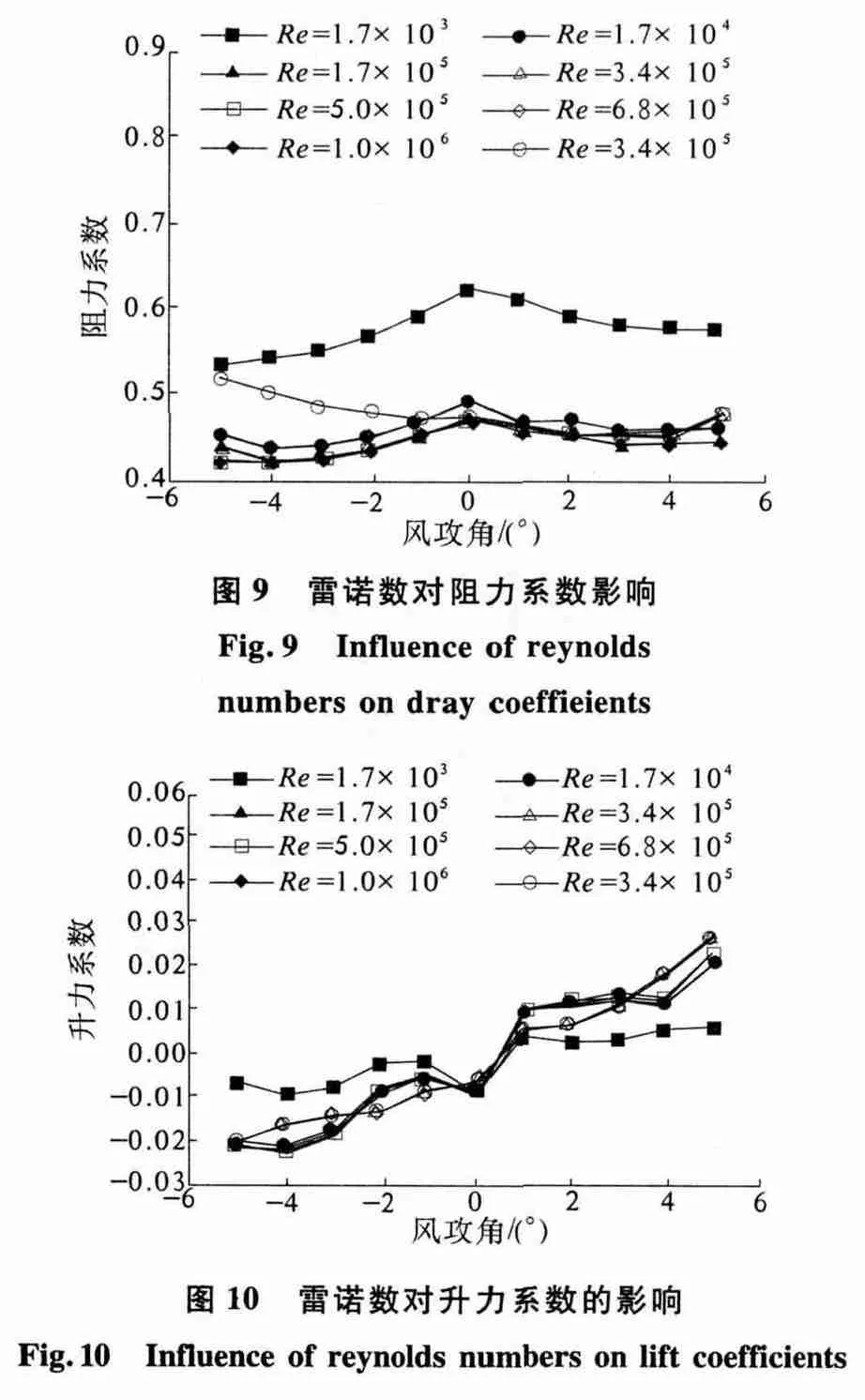
由图9 可见，当雷诺数为104～106数量级时，0°攻角附近，不同雷诺数阻力系数相差很小;在-5° ～0°攻角范围内，雷诺数较小时，阻力系数较大，随着雷诺数的增大，阻力系数减小，雷诺数达到105数量级时，阻力系数非常接近;在0° ～5°攻角范围内，随着雷诺数的增大，阻力系数减小，且雷诺数较大时，阻力系数相差微小．整体来看，随雷诺数的增大，阻力系数CFD 模拟的相对误差最大为15．4%，模拟值和试验值［17］相对误差最大为13．8%，误差不大．

由图10 可见，当雷诺数为104～106数量级时，在-5° ～0°攻角范围内，随着雷诺数的增大，升力系数增大，当雷诺数较大时，升力系数几乎相同;在0° ～5°攻角范围内，雷诺数的大小和升力系数没有明显变化规律，但不同雷诺数之间升力系数差别很小．整体来看，随着雷诺数的增大，个别升力系数CFD 模拟的相对误差最大为41．3%，模拟值和试验值相对误差最大为41．6%，但从图上总体来看，模拟值与试验值变化趋势基本吻合，模拟结果是可以接受的．

另外，由图9 和图10 可知，当雷诺数为103数量级时，阻力系数和升力系数均和风洞试验数据有相当大差距．阻力系数普遍偏大，相对误差都在20%以上;个别升力系数差值甚至达到4 倍．阻力系数与升力系数变化无规律可循，对其模拟数据分析意义不大．

由上述分析可知，当雷诺数大小数量级与风洞试验一致，或相差不大时，雷诺数的变化对阻力系数影响较小，但对个别升力系数影响较大，雷诺数越接近风洞试验，雷诺数的数量级误差越小，因此在进行猫道的数值模拟时，选择与风洞试验一致的雷诺数很有必要．

4 结论

(1)当数值模拟时设置的雷诺数大小数量级与试验工况本身实际的雷诺数一致，或与试验工况本身雷诺数本身相差不大时，雷诺数的变化对阻力系数相对误差影响较小，但对个别升力系数影响相对较大，所以在进行猫道的数值模拟时，选择接近与试验工况本身实际的雷诺数很有必要;

(2)在-5° ～5°风攻角范围内，SST 湍流模型为猫道断面阻力和升力系数CFD 方法识别的较合理的模型．

［1］ 杨学祥，张明卓，朱艳，等．大跨度悬索桥施工猫道若干问题综述［J］．世界桥梁，2007(2):61 -64．

［2］ 吴胜东，冯兆祥，蒋波．特大跨径悬索桥上部结构施工关键技术研究［J］． 土木工程学报，2007，40(4):32 -37．

［3］ 贾宁，刘健新，刘万锋．悬索桥施工猫道静风失稳机理分析［J］．公路交通科技，2008，25(3):99 -102．

［4］ 李胜利． 大跨径悬索桥施工期暂态结构抗风性能及控制［D］． 哈尔滨:哈尔滨工业大学土木工程学院，2010．

［5］ 李胜利，胡亚楠，王东炜．台风-波浪耦合作用下钢管桩施工平台力学行为分析［J］．郑州大学学报:工学版，2014，35(6):82 -85．

［6］ 何晗欣，刘健新． 大跨度悬索桥抗风措施及其优化研究［J］． 公 路 交 通 科 技，2011，28 (3):93 -97，102．

［7］ 赵凯，李永乐，欧阳韦，等．大跨度斜拉桥的静风失稳特性［J］．公路交通科技，2011，28(8):67 -72．

［8］ SELVAM R P，BOSCH H，JOSHI R． Comparison of 2D and 3D CFD Modeling of Bridge Aerodynamics［C］∥The 5th International Symposium On Computational Wind Engineering (CWE2010)． Chapel Hill:North Carolina，2010:23 -27．

［9］ 李加武，崔欣，张宏杰，等． 粗糙度对雷诺数效应的影响［J］．长安大学学报:自然科学版，2009，29(2):56 - 59．

［10］李薇，胡兆同，李加武． CFD 方法研究桥梁断面三分力系数的雷诺数效应［J］． 长安大学学报:自然科学版，2010，30(6):44 -49．

［11］谭红霞，陈振清． CFD 在桥梁断面静力三分力系数计算中的应用［J］． 工程力学，2009 ，26(11 ):68 -72．

［12］廖海黎．舟山西堠门大桥猫道抗风稳定性风洞模型试验［R］．成都:西南交通大学风工程试验研究中心，2005．

［13］瞿伟廉，刘琳娜．基于CFD 的桥梁三分力系数识别的数值研究［J］． 武汉理工大学学报，2007，29(7):85 -88．

［14］林斌，孙晓颖，武岳． 大庆石油学院体育馆屋面风荷载的风洞试验及CFD 数值模拟［J］． 沈阳建筑大学学报:自然科学版，2006，22(3):357 -361．

［15］ WATANABE S，FUMOTO K． Aerodynamic study of slotted box girder using computational fluid dynamics［J］． Wind Engineering and IndustrialAerodynamics，2008，96:1885 -1894．

［16］ SIRIBOONLUCKUL N，JUNTASARO V． Turbulence modeling for wall-bounded particle-laden flow with separation［J］． International Communications in Heat and Mass Transfer，2007，34(3):331 -338．

［17］ BAGLIETTO E，NINOKATA H． A turbulence model study for simulating flow inside tight lattice rod bundles［J］． Nuclear Engineering and Design，2005，235(7):773 -784．