静止同步补偿器新型双闭环控制策略研究

曹 原，尉乔南

(南阳理工学院 电子与电气工程学院，河南 南阳473004)

0 引言

静止同步补偿器(STATCOM)是采用逆变器电路组成的无功补偿装置，通过对逆变器中全控型开关管控制，可以快速实现该装置在不同工况下的运行［1-2］． 目前对于STATCOM 无功补偿系统中的控制策略问题研究已有很多文献论述，文献［3］在直接转矩控制的基础上引入了空间矢量控制及预测控制思想，可以克服直接转矩控制中开关频率不固定的不足． 但是这在一定程度上也增加了控制系统的复杂性和实现难度．文献［4 -5］中对基于解耦控制的间接电流控制策略进行了详细的分析，但是这种控制策略中有个固定的缺陷，就是其中的解耦控制算法需要精确知道逆变系统与电网之间连接电感的值，但是由于制作电感的材料和工艺的差别以及系统运行中电感量会变化，这将导致电感值无法精确获取，随着逆变系统输出的电流过大、连接电感饱和、电感量变化，由此会导致控制系统失去控制或者更严重的情况发生．笔者主要在上述文献的基础上，就传统解耦控制需要精确知道连接电感量值或者电感值变化导致系统失去控制等问题，提出一种改进方法，这种新型的控制策略无需知道电感值，去除了电感量变化带来的控制影响，而后简单介绍了该装置的调制算法，并重点就60°坐标系下虚拟SVPWM 两种调制算法下平衡其直流母线电容压差的算法做了仿真研究，接着按照上述的理论在PSIM 中搭建了新型解耦控制系统仿真模型，最后通过实验验证了理论的正确性和可行性．

1 三电平STATCOM 结构与运行原理

电压源型桥式电路结构在电力系统无功补偿装置中应用比较广泛，电压源型逆变器电路直流侧为电容．笔者研究的也主要是基于电压源型桥式电路的三相三电平静止同步补偿器，其采用L型滤波器并联接入电力系统中的功率电路连接图如图1 所示．

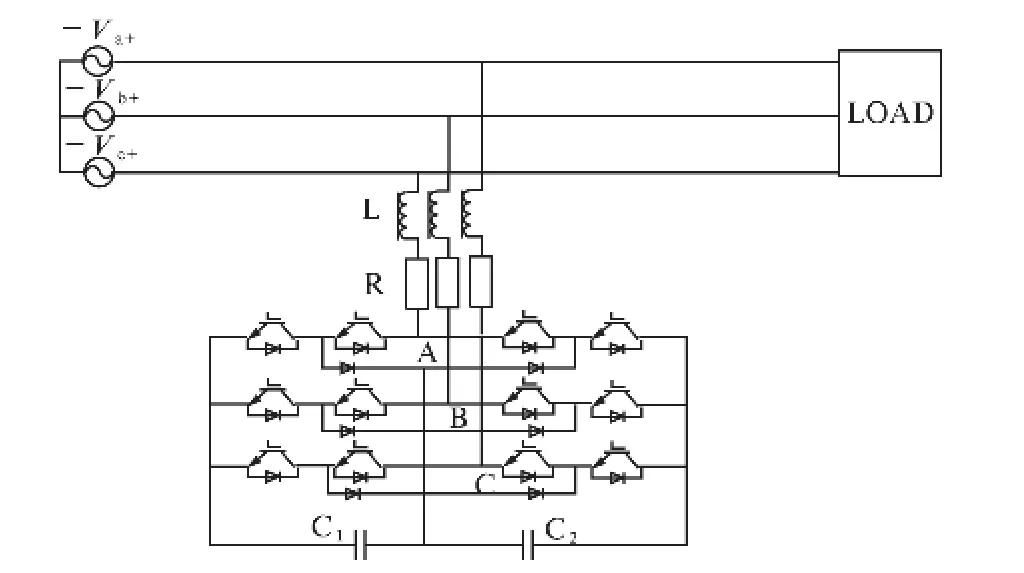
图1 三电平静止同步补偿器拓扑结构Fig．1 Three-level STATCOM topology structure

静止同步补偿器的工作原理就是通过控制装置中的开关管使得逆变器交流侧输出电流快速地跟踪上系统中检测到的无功电流指令值，有效地抵消电力系统中的无功电流，从而实现对系统的无功功率的动态补偿．

2 系统数学模型与新型控制策略分析

2．1 系统数学模型

踪上无功电流指令，由此可能会让整个系统崩溃［6］．

三电平静止同步补偿器系统电路连接图如图1 所示．不计输电线路阻抗时，静止同步补偿器接入点电压即为电网电压． 电网电压为三相对称正弦波，令其相电压有效值为vsa，vsb，vsc，也即:vsa=vsb=vsc=vs;静止同步补偿器装置交流侧输出的三相基波电压有效值为vca，vcb，vcc．

电流取从电网流入到逆变器的方向，可得:

图2 DQ 坐标下传统解耦控制框图Fig．2 Traditional decoupling control block under DQ coordinate system

该系统在三相ABC 静止坐标系下的数学模型，再经过坐标变换可得该系统在DQ 坐标系下的简化数学模型，详细推导见参考文献［4］，这里不再赘述．

下面就基于STATCOM 数学模型的基础上提出一种无需知道电感值L 的新型控制策略，由上述可知STATCOM 在DQ 坐标系下的数学模型如式(2)所示．

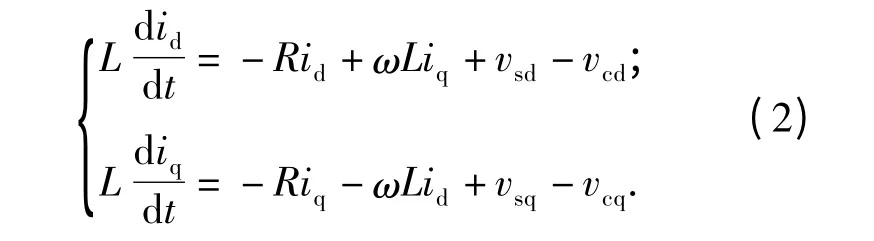
对静止同步补偿器的数学模型，引入中间变量x1，x2，其中经坐标变换vsd=vs，vsq=0，其中vs是电网相电压的有效值，代入可得:

式中:vsd，vsq为电网电压在DQ 坐标系下的分量;vcd，vcq为逆变器交流侧基波电压在DQ 坐标系下的分量;ω 为旋转角速度．

根据式(2)的数学模型，可得出其控制系统结构框图，该装置的控制系统一般设计为电压外环和电流内环控制． 电压外环主要完成逆变器直流侧电容电压稳定的控制，电流内环主要完成指令电流的跟踪控制． 传统的双闭环解耦控制框图如图2 所示．

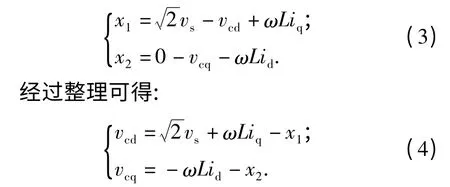
上式中需要知道电感L 的准确值，因此对上式中电感值L 的设计如下的PI 控制参数:

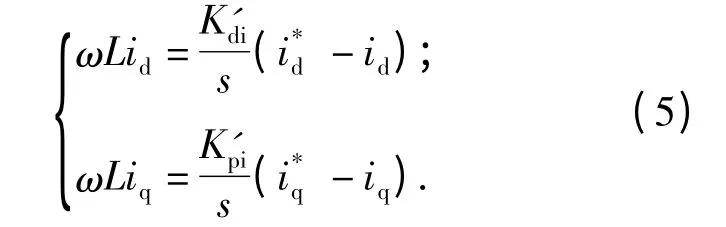
vdc-ref为设定的逆变器直流侧电压给定值为直流侧电压采样值与vdc-ref的差经控制器后得出的有功指令是通过无功电流检测环节得到的指令值．

2．2 新型控制系统设计

对于x1，x2，可以设计如下的PI 控制参数:

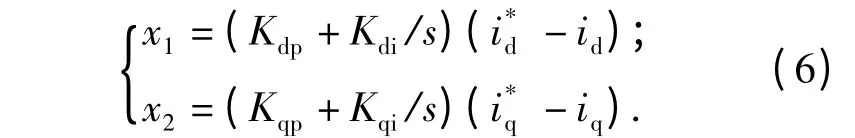
将式(5)和式(6)带入式(4)中可得:

由上述STATCOM 在DQ 坐标下传统双闭环解耦控制框图可知，传统控制系统中需要知道连接电感的准确值，由于工艺和材料的差异，电感值L 无法准确测得，而且STATCOM 系统在运行过程中由于电流过大会导致电感出现饱和等情况，这将会导致STATCOM 输出的无功电流无法准确跟

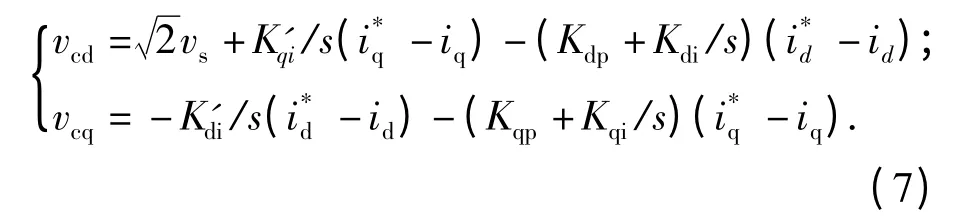
根据式(7)可以得出STATCOM 新型解耦控制策略框图如图3 所示．

从上图中可以看到，DQ 轴耦合部分可以分别进行参数整定，其中含有电感L 的部分被替换，因此该控制策略中电感量的影响就不存在了．

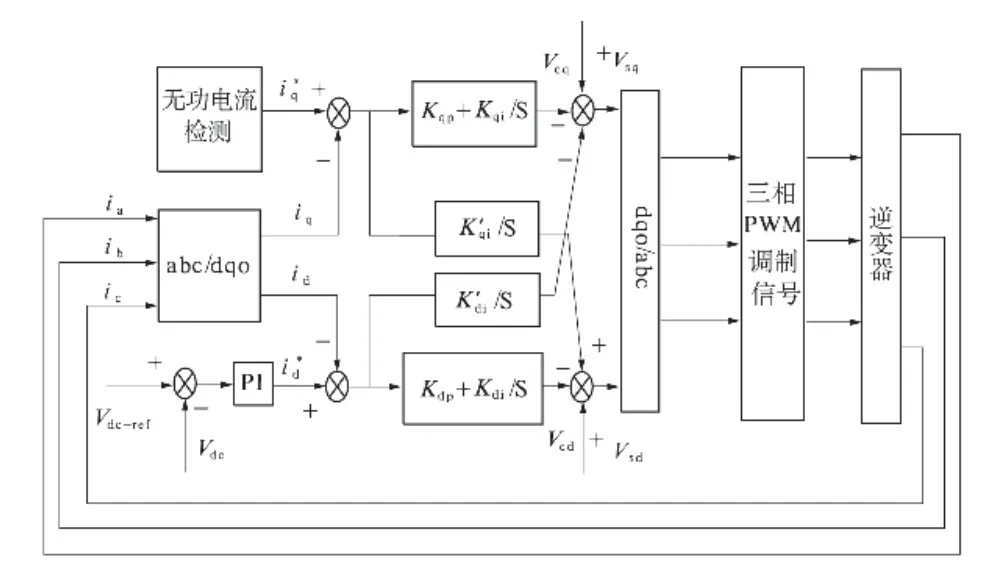
图3 DQ 坐标下新型解耦控制框图Fig．3 Novel decoupling control block under DQ coordinate system

3 SVPWM 调制算法与压差平衡控制

空间电压矢量调制法(SVPWM)是用逆变器不同开关状态所产生的实际电压矢量终点的运行轨迹去逼近电压矢量的理想标准圆［7-9］．

笔者采用60°坐标系下虚拟空间矢量调制算法，在60°坐标系下，大小区域判断只需要比较整数数值的大小，方便了计算和编程．而且虚拟空间矢量调制策略主要作用就是在每个开关周期内，采用3 个可以相互抵消对直流侧中点电位影响的电压矢量合成目标矢量，从而保证任何开关周期内中点电位都处于平衡状态． 其中60°坐标系下三电平逆变器矢量图如图4 所示．

矢量在α -β 坐标系 和g -h 坐标系下的对应关系如式(8)所示．

考虑两电平内任意参考电压矢量Uref=［ug，uh］，首先确定参考电压矢量位于哪个扇区，每个扇区的判断逻辑运算见表1．

考虑在两电平的S1 扇区内，选择合成参考矢量的电压矢量为U1=［0，0］，U2=［2uc，0］，U3=［0，2uc］，根据伏秒平衡原理可得

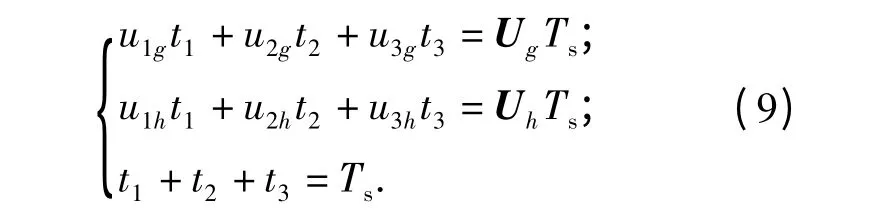
式中:Ts为采样周期;t1，t2，t3分别为U1，U2，U3对应的作用时间;u1g，u2g，u3g分别为U1，U2，U3在g轴上的投影值;u1h，u2h，u3h分别为U1，U2，U3在h轴上的投影值．

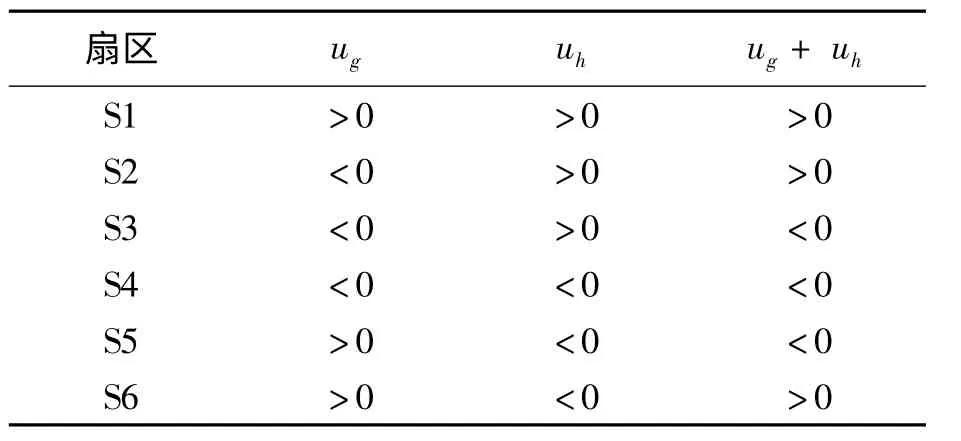
表1 扇区判断逻辑运算Tab．1 Logical operation for sector determine

图4 60°坐标系下三电平空间电压矢量图Fig．4 Space vector states for three-level based on 60° coordinate frame

后续的算法步骤详细参见参考文献［7］． 采用60°坐标系下虚拟空间矢量调制算法后的直流侧上下电容电压的波动范围很小，平衡直流侧电容电压效果好了很多． 直流侧电容电压的波动是无法避免的，只有将其稳定在一定的范围之内才能使三电平逆变器可靠的运行．

4 系统仿真与实验验证

在PSIM 中搭建了基于新型双闭环控制策略无功补偿系统的仿真模型，其主参数为:电网线电压有效值380 V，基波频率50 Hz，装置的无功容量为±50 kVar，采用60°坐标系下虚拟空间矢量调制算法，载波频率取10 kHz．

根据上述所搭建的三电平静止同步补偿器系统仿真模型进行系统的双闭环控制仿真． 整个仿真的时间设为0．5 s，并设置在0．25 s 时改变负载特性由阻感负载变为阻容负载，以验证三电平静止同步补偿器是否能够在两种工况下运行．

无功补偿前后电网的A 相电压和电流波形如图5 所示，系统运行时的直流侧上下电容电压波形如图6 所示．

为了进一步验证该系统的可行性，搭建了三相三电平静止同步补偿器实验平台，其中控制策略采用的就是上述新型双闭环的控制算法，并进行无功补偿装置的实验［10-11］．具体实验参数如表2 所示．

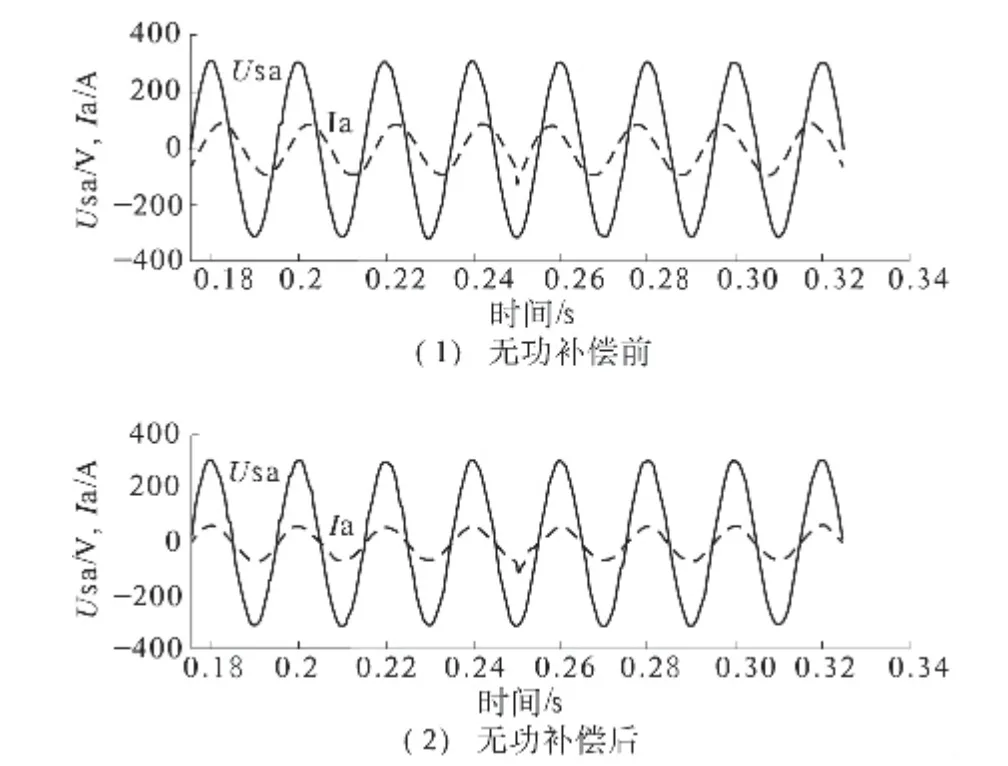
图5 无功补偿前后系统A 相电压和电流波形Fig．5 Voltage and current waveform of A phase before and after reactive power compensation

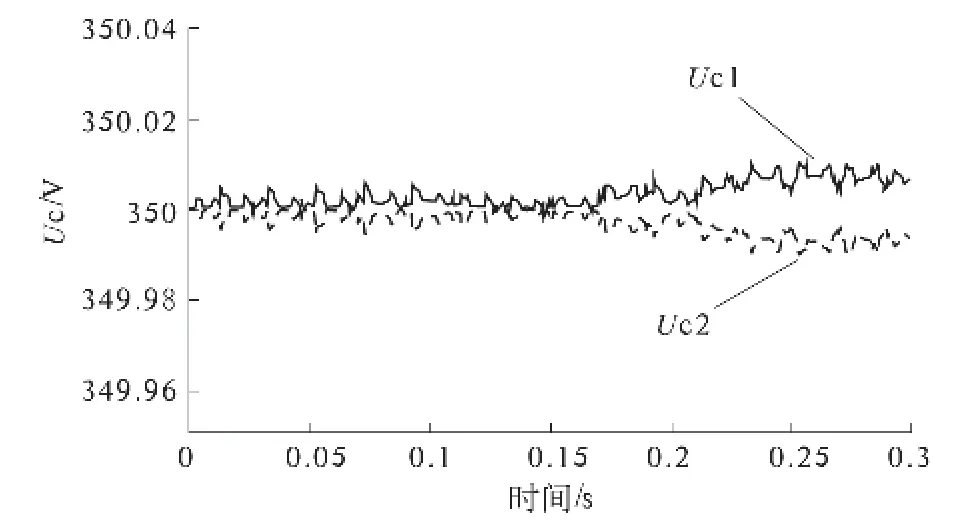
图6 直流母线电容电压波形图Fig．6 Capacitor voltage waveforms of DC bus

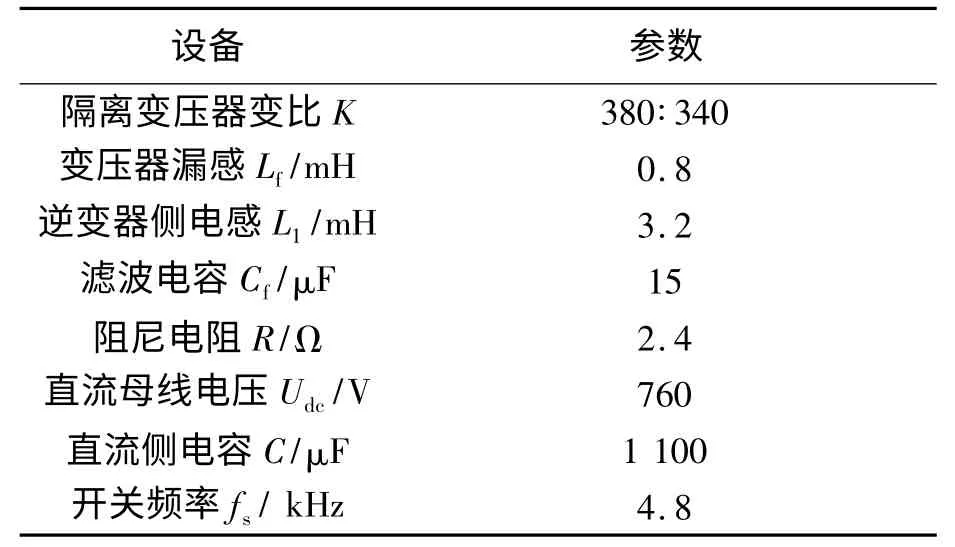
表2 实验参数Tab．2 Experimental parameters

系统带阻感性负载，补偿前系统A 相电压和电流的波形如图7 所示，由于感性无功电流的存在，负载电流滞后系统电压一定的角度．

补偿之后系统A 相电压和电流的波形如图8所示，从图中看出电流和电压同相位，说明负载无功功率得到了完全补偿，也证明了解耦控制策略的正确性．

60°坐标系VSVPWM 平衡控制代码的直流母线上下电容电压的波形如图9 所示． 在该调制算法下直流母线上下电容电压相差7．3 V，由此证明了直流母线电容电压平衡控制算法的有效性，也只有在直流母线电容电压处于容许的范围内波动时才能使整个系统更可靠地运行．

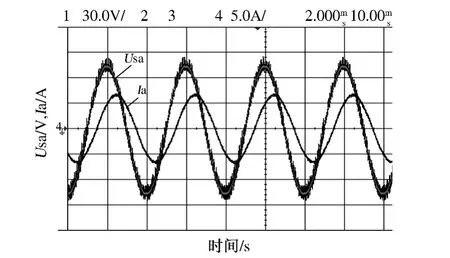
图7 补偿前系统A 相电压和电流波形Fig．7 Voltage and current waveform of A phase before reactive power compensation

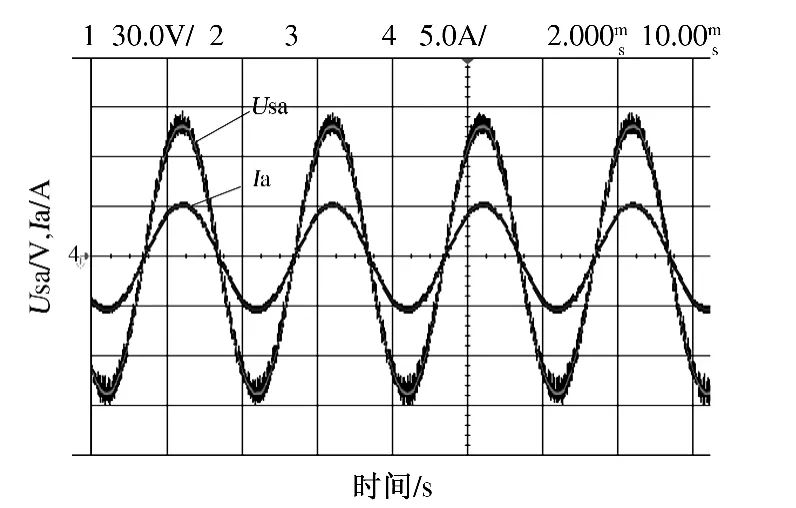
图8 补偿后系统A 相电压和电流波形Fig．8 Voltage and current waveform of A phase after reactive power compensation

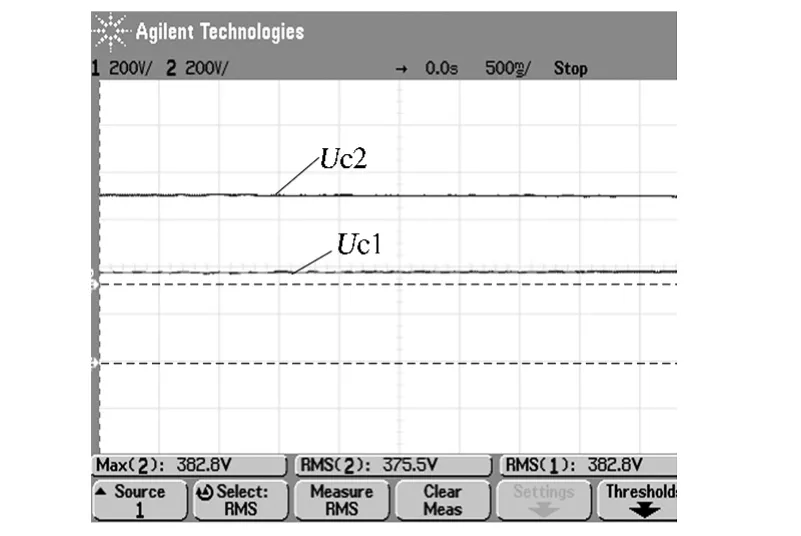
图9 加平衡控制代码后系统稳态直流母线电容电压波形Fig．9 System steady capacitor voltage waveforms of DC bus with balance control code

5 结论

笔者主要在前人文献的基础上，就传统解耦控制的连接电感量值不精确或者变化导致系统失去控制等问题提出一种改进方法，这种新型的控制策略无需知道电感值，消灭了电感量变化带来的控制影响． 而后简单介绍了60°坐标系下虚拟SVPWM 调制算法，接着按照上述的理论在PSIM中搭建了新型解耦控制系统仿真模型，通过典型的PI 控制和虚拟SVPWM 方法实现了整个系统的控制，仿真结果验证了PI 参数整定和解耦控制策略的正确可行性．最后进行了系统模拟实验，实验结果与理论分析基本相符，该方法对多电平逆变技术在电力系统中的应用，起到重要的作用．

［1］ 王兆安，杨君，刘进军，等． 谐波抑制和无功功率补偿［M］．北京:机械工业出版社，2005．

［2］ 陈坚． 电力电子学——电力电子变换和控制技术［M］．2 版． 北京:高等教育出版社，2002．

［3］ BOUAFIA A，GAUBERT J P，KRIM F． Predictive direct power control of three-phase pulse width modulation (PWM)rectifier using space-vector modulation(SVM)［J］．IEEE Transactions on Power Electronics，2010，25(1):228 -236．

［4］ 许湘莲． 基于级联多电平逆变器的STATCOM 及其控制策略研究［D］． 武汉:华中科技大学电气与电子工程学院，2006．

［5］ 张益华，孙玉坤，张亮．一种新型的NPC 三电平矿用无功补偿器及其解耦控制研究［J］． 电测与仪表，2014，51(3):54 -58．

［6］ 陈耀军，钟炎平．基于合成矢量的电压型PWM 整流器电流控制研究［J］． 中国电机工程学报，2006，26(2):143 -148．

［7］ 胡存刚，王群京，李国丽，等． 基于虚拟空间矢量的三电平NPC 逆变器中点电压平衡控制方法［J］．电工技术学报，2009，24(5):100 -107．

［8］ CELANOVIC N，BOROYEVICH D． A comprehensive study of neutral-point voltage balancing problem in three-level neutral-point-clamped voltage source PWM inverters［J］． IEEE Transactions on Power Electronics，2000，15(2):242 -249．

［9］姜卫东，王群京，陈权，等． 考虑中点电压不平衡的中点箝位型三电平逆变器空间矢量调制方法［J］．中国电机工程学报，2008，28(30):20 -26．

［10］同向前，焦妍莹，申炜． 静止同步补偿器滤波电感的选择［J］．电力电子技术，2007，41(2):93 -95．

［11］荣飞． 配电网静止同步补偿器技术研究［D］．长沙:湖南大学电气与信息工程学院，2008．