一种大地坐标变换近似算法

马 娟，倪世道，任小叶

(中国电子科技集团公司第38研究所，合肥 230031)



一种大地坐标变换近似算法

马 娟，倪世道，任小叶

(中国电子科技集团公司第38研究所，合肥 230031)

机载雷达数据处理系统需要频繁使用大地坐标变换算法将测量数据转换到公共参考坐标系下。针对精度要求相对较低但计算负载大的机载预警雷达系统，提出一种近似大地坐标变换算法以解决常规算法计算复杂度大、需要迭代实现等问题。数值计算结果表明：文中所提算法精度损失较小，计算复杂度低。

大地坐标变换；近似算法；计算复杂度；精度

0 引 言

机载雷达系统中，载机处于运动状态，雷达测量值的坐标中心不断发生变化，同时接收其它传感器的参考信息可能采用不同的坐标系。因此，为获得可靠的目标信息，需要将测量数据转换到公共参考坐标系下[1]。坐标变换算法直接影响雷达系统的计算效率和情报质量。目前，应用较多的坐标变换方法有球极投影法、大地坐标变换法及平移变换法等。作为一种高精度的坐标变换方法，大地坐标变换方法已经在很多领域获得成功应用[2-3]。该方法以大地坐标系为统一坐标系进行变换，即利用大地坐标完成从传感器测量值所在坐标系到跟踪或指控中心所在坐标系的转换。传统的大地坐标变换算法从地心直角坐标系转换到地理坐标系时需要多次迭代实现，本文所提近似算法不需要迭代计算，在保障精度损失较小的情况下显著降低了算法的计算复杂度。

1 标准大地坐标变换算法

常用的大地坐标有2种表示方式：地心直角坐标系(ECEF)与地理坐标系(LGLT)[3]。图1为大地坐标示意图。地心直角坐标系是一种惯性坐标系，原点选在地球球心，X轴沿赤道平面指向本初子午线，Z轴沿地球自转轴指向北极，Y轴在赤道平面内与X轴垂直并形成右手坐标系。地理坐标系用经度、纬度和高度表示。经度L定义为点T在赤道平面上的投影T′与X轴的夹角；过参考椭球上一点M的垂线TM与赤道平面相交的角度B为地理纬度(也称大地纬度)，过参考椭球体上一点N与地心O的连线OT与赤道平面的夹角B′为地心纬度。一般情况下，纬度默认为地理纬度。

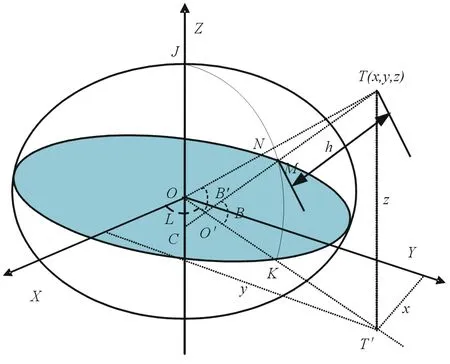
图1 大地坐标示意图

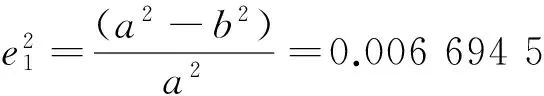
假设雷达的经度、纬度和高度分别为L、B、h，则其在地心直角坐标系中的坐标为：

(1)

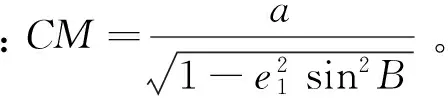
式(1)将地理坐标系参数转换到地心直角坐标系，该过程中未带入任何误差。

假设雷达在地心直角坐标系中的坐标为x、y、z，则其在地理坐标系中可表示为：

(2)

由于从地心直角坐标系到地理坐标系的转换方程式为非闭形式，故由x、y、z获得对应的L、B、h较为困难，需经过多次迭代实现。

2 大地坐标变换近似算法

2.1 椭圆相关公式

图2为经过T所在经度线，并通过地轴的局部切面图，即图2上弧MN所在经度的切面。JOK为1/4椭圆，点P、Q分别为过点M的椭圆切线与W轴、Z轴的交点，过点M作W轴的垂线，R为垂足。根据椭圆和椭球性质，可得JOK所在椭圆方程和过椭圆上点M(w0，z0)的椭圆切线方程：

(3)

(4)

式中:w2=x2+y2。

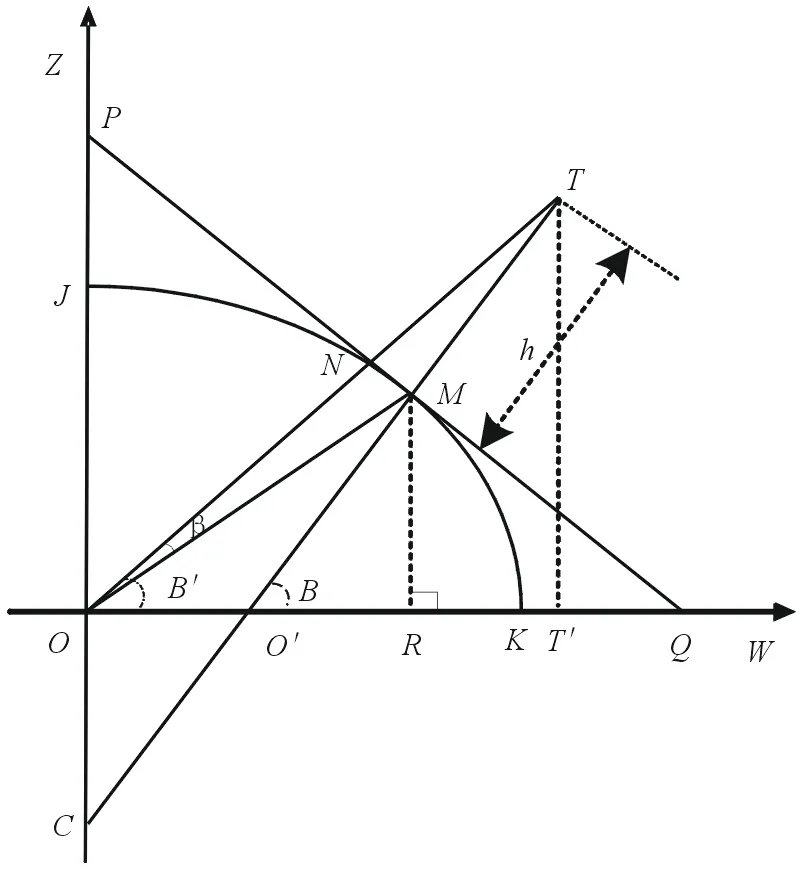
图2 沿经度线过地轴的1/4切面图

根据相似三角形原理和式(4)，可得:

(5)

因此:

(6)

(7)

(8)

将式(7)代入椭圆方程，可得:

(9)

(10)

由三角函数公式和式(8)、(9)，可得:

(11)

根据相似三角形原理和式(6)，可得：

(12)

(13)

由三角函数公式和式(13)，可得：

(14)

由三角函数正切公式和式(8)、式(14)可得：

2.2 LGLT到ECEF变换公式

雷达载机和目标所在高度h一般小于1.5×104m，而CM大于6×107(见式(10))，由式(14)可得：

(16)

因此，地心纬度B′可由下式近似计算：

(17)

由式(15)可知：

(18)

由于β值很小，所以:

OT≈OM+h

(19)

(20)

从LGLT到ECEF近似变换公式为：

(21)

通过上述变换，x、y、z的误差数量级为101m，误差为十万分之一。

2.3 ECEF到LGLT变换公式

根据与前面相同的近似关系，可得：

(22)

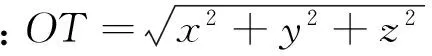
通过上述反变换，L无误差，B的误差值数量级为10-6，h的误差值数量级为10-2m。

3 对比实验

取中国范围内的经度(73°～135°)、纬度(4°～53°)和雷达探测范围内的高度(0～15 000 m)，将本文所提近似算法与精确计算的结果比较，统计近似算法的转换误差。其中精确计算时从地心直角坐标系转换到地理坐标系采用迭代实现，纬度计算误差小于(10-6)°。

为了充分说明近似算法的误差范围，对比实验包括3个：

(1) 经度变化，观察转换误差与经度关系。目标纬度为28°，高度为8 000 m，经度以相同步长变化50次，变化范围为73～135°。比较近似算法从LGLT到ECEF和从相应的真实ECEF到LGLT转换误差。

(2) 纬度变化，观察转换误差与纬度关系。目标经度为104°，高度为8 000 m，纬度以相同步长变化50次，变化范围为4～53°。比较近似算法从LGLT到ECEF和从相应的真实ECEF到LGLT转换误差。

(3) 高度变化，观察转换误差与高度关系。目标经度为104°，目标纬度为28°，高度以相同步长变化50次，变化范围为0～15 000 m。比较近似算法从LGLT到ECEF和从相应的真实ECEF到LGLT转换误差。

图3为3组对比实验的经度转换误差。从图上可以明显看出，经度转换无误差。

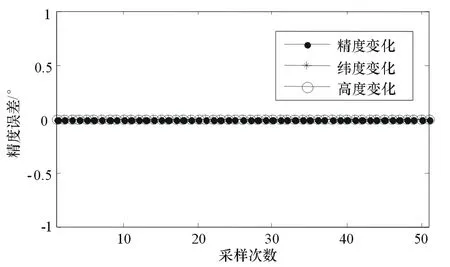
图3 近似算法的经度转换误差

图4为3组对比实验的纬度转换误差。

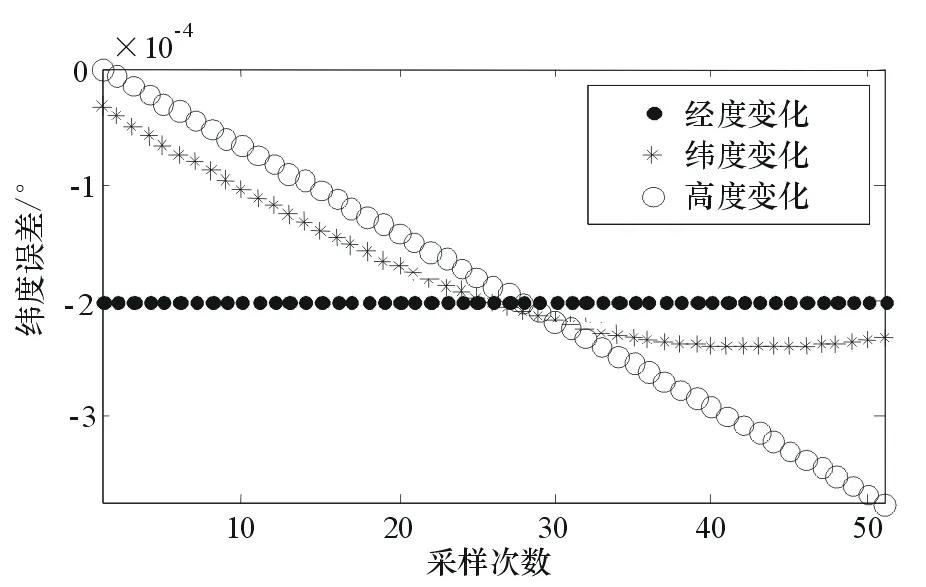
图4 近似算法的纬度转换误差

在本文的实验条件下，纬度转换的最大误差为(-3.75×10-4)°。

图5为3组对比实验的高度转换误差。

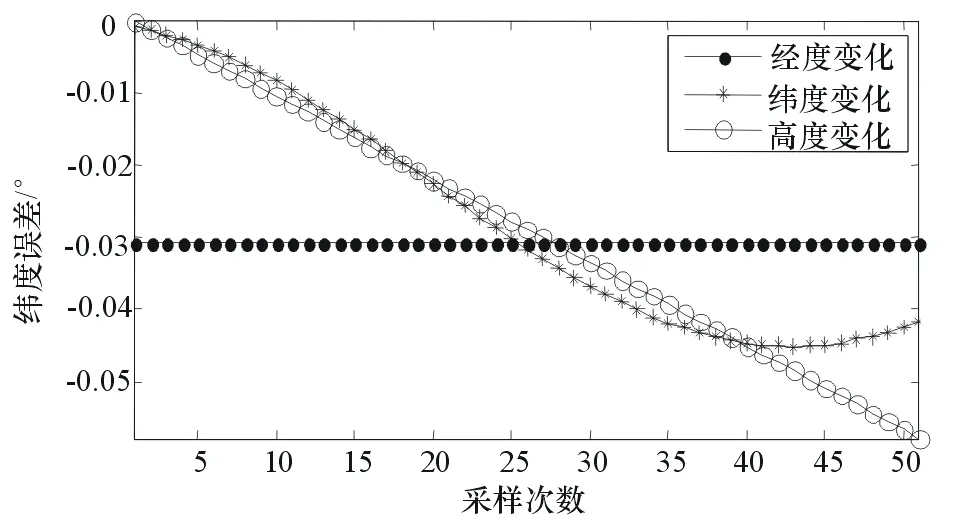
图5 近似算法的高度转换误差

在本文的实验条件下，高度转换的最大误差为-0.057m。

图6为3组对比实验的X坐标转换误差。在本文的实验条件下，X坐标转换的最大误差为7.36 m。

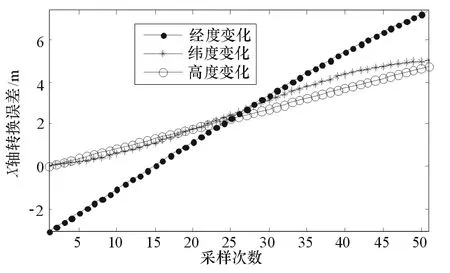
图6 近似算法的X坐标转换误差

图7为3组对比实验的Y坐标转换误差。在本文的实验条件下，Y坐标转换的最大误差为-20 m。

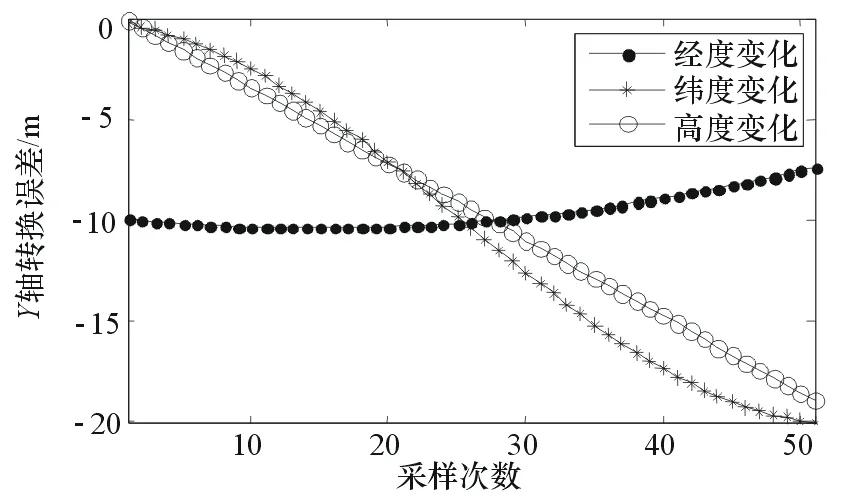
图7 近似算法的Y轴转换误差

图8为3组对比实验的Z坐标转换误差。在本文的实验条件下，Z坐标转换的最大误差为36.83 m。

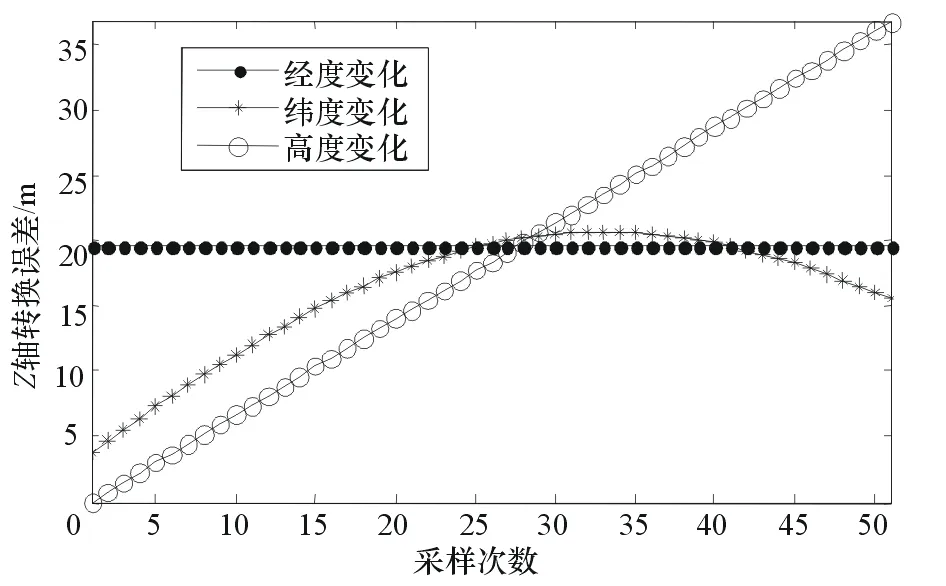
图8 近似算法的Z轴转换误差

综合图3～图8可以看出，不管是从LGLT转换到ECEF还是从ECEF转换到LGLT，本文算法的精度损失都很小，完全满足常规雷达的精度转换要求。

4 结束语

标准大地坐标变换算法中，由地理坐标系参数可以较容易地获得地心直角坐标系参数，而从地心直角坐标系转换到地理坐标系则需要经过多次迭代才能获得精度许可范围内的参数。本文所提的近似算法不需迭代即可实现两者之间的相互转换，显著 降低了计算量，数学分析和仿真实验证明该算法具有较高的精度，适用于坐标变换频繁使用或对精度要求不是特别高的机载雷达数据处理系统。

[1] 何友，修建娟，关欣，等.雷达数据处理及应用[M].北京：电子工业出版社，2013.

[2] 王放，魏玺章，黎湘.传感器组网坐标变换及其精度分析[J].系统工程与电子技术，2005,27(7):1231-1234.

[3] 苏海军，林宏亮，李侠，等.基于ECEF的雷达组网目标综合定位精度分析[J].空军雷达学院学报，2007，21(2):88-89.

[4] 张勤，李家权.GPS测量原理及应用[M].北京：科学出版社，2010.

[5] 韩崇昭，朱洪艳，段战胜，等.多源信息融合[M].北京：清华大学出版社，2006.

An Approximate Algorithm of Geodetic Coordinate Transformation

MA Juan,NI Shi-dao,REN Xiao-ye

(No.38 Research Institute of CETC,Hefei 230031，China)

The geodetic coordinate transformation algorithm is used frequently to transform the measured data into the data in common reference coordinate in airborne radar data processing system.For airborne early warning radar system with lower accuracy request and large calculation load,this paper presents a kind of approximate algorithm of geodetic coordinate transformation to resolve the problems such as large calculation complexity and iteration implementation,etc..The numerical value calculation result shows that the accuracy loss of the algorithm presented in this paper is small and the calculation complexity is low.

geodetic coordinate transformation；approximate algorithm；calculation complexity；accuracy

2015-04-30

TN959.72

A

CN32-1413(2015)04-0040-04

10.16426/j.cnki.jcdzdk.2015.04.011