常微分方程数学建模案例分析

刘洪霞， 周绍伟

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

常微分方程数学建模案例分析

刘洪霞， 周绍伟

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

在常微分方程教学中，选取与实际生活密切相关的问题，采用数学建模的思想解决，对学生应用数学的能力和学习兴趣的提高具有积极的作用.案例教学能使学生理论联系实际，更好地掌握常微分方程理论.

常微分方程；数学建模；实际案例

0 引言

传统的大学数学教学强调理论知识的推导和计算技巧的掌握，忽视数学思想的来源及在实际生活中的应用，学生在学习过程中通常感到抽象难懂，而当面对实际问题时，更不知如何用数学知识解决.因此，在高等数学课堂教学中开展实际案例教学是大学数学教学改革的重要方向.案例教学是由贴近生活的实际情境引出数学问题，转化为数学知识，然后用所学的数学知识处理各种实际问题，缩短教学情境与实际生活情境的差距，提高学生学习的兴趣，同时培养学生的实践能力与创新能力.

常微分方程是高等数学中的一个重要内容，学生在学习时往往只知道如何解方程，并不懂这些方程的实际背景，因此造成学生缺乏学习兴趣与动力.案例教学在授课过程中从实际案例出发，加强学生对微分方程实际应用的了解，同时加深学生对数学建模思想的理解，从而提高学生数学建模能力，以及分析问题和解决实际问题的能力.将数学建模思想渗透在常微分方程教学中,确保学生对常微分方程教学的方法、背景以及意义有一定了解，提高学生对数学的学习兴趣和应用数学知识解决实际问题的能力.

笔者选取常微分方程中的若干习题，将其用数学语言阐述，并按数学建模解决问题的思想对其作合理假设，构造微分方程模型，并用学生所学的知识进行模型求解，将课程内容和数学建模内容进行有机融合，最终将数学建模方法与思想表达出来，使学生在学习课堂知识的同时掌握数学建模的思想.

1 数学建模案例分析

1.1 湖水污染问题

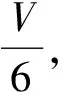
模型假设 1)假设河水是湖水的唯一水源且湖水容量不变；

2)假设湖泊中A的浓度是均匀的；

3)假设河水流进湖后立即与湖水充分混合从而使有毒污染物全部溶解在湖水中.

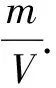
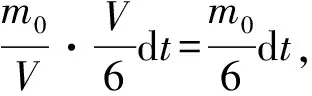
得

t=6ln 3．

故最多需经过6ln 3年，湖泊中污染物A的含量可降至m0以内．

1.2 信号灯问题

问题2 在北京、上海、深圳等大城市乘坐公共汽车，等交通信号灯一直是一个比较烦恼的问题.交通路口的指挥信号灯有红、黄、绿3种颜色，在绿灯转换为红灯之前有一个过渡状态，这个过渡状态是由黄灯来完成的，通常是亮一段时间黄灯以后才变成红灯信号.交通指挥灯信号设置合理，既可保证交通安全又可避免某一方向的车流等待时间太长，减少司机、乘客的烦恼.如果交通指挥灯闪烁时间设置不合理，虽然可保证交通安全，但往往会造成人们等待时间太长，增加司机、乘客的烦恼[3].那么怎样设置交通指挥灯中各种颜色信号闪烁时间的长短，特别是黄灯闪烁多长时间才合理？

模型分析 黄灯信号的作用之一是提醒驾驶员注意红绿信号灯，当遇到红灯时应立即停车让横向车流和人流通过，但已越过停止线的车辆可以继续通过；黄灯信号的作用之二是：当黄灯亮时，机动车、行人在保证安全的原则下通行.

停车是需要时间的，在这段时间内，车辆仍将向前行驶一段距离L,假设道路的宽度是D.现在的问题是如何确定L的大小.

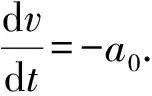
模型求解 两边同时积分得v(t)=-at+c.由初始条件v(0)=v0，得c=v0，这样

v(t)=v0-at.

所以，

那么黄灯究竟能亮多久呢？通过上面的推导可知，黄灯闪烁时间包括从驾驶员看到黄灯开始到汽车停下来所用时间和让已经过线的车顺利穿过路口所用时间，因此黄灯闪烁时间至少应该为

1.3 传染病预报模型

问题3 一只游船上有800名乘客，其中有一名乘客患了某种传染病，12 h后3人发病.由于这种传染病没有早期症状，因此传染者无法被及时隔离，救援人员将在60～72 h将疫苗送到，请估计疫苗送到时患这种传染病的人数.

模型分析 设y(t)表示发现首例病人后th感染的人数，则800-y(t)表示此时刻未受感染的人数.由题意知，y(0)=1,y(12)=3.当感染人数y(t)很小时，传染病的传播速度较慢，但当感染人数y(t)较大时，传播速度加快，因此感染人数与当时病人数成正比，比例系数即为单位时间内一个病人能传染健康人数的数目.

模型建立 单位时间内的发病人数和当时受感染者的人数以及未受感染的人数之积成正比，设比例系数为k.考虑t到t+Δt时刻，感染人数的增加量Δy=y(t+Δt)-y(t)，根据上面的分析，应该有

Δy=y(t+Δt)-y(t)=ky(800-y(t))Δt，

则有

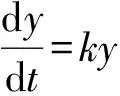
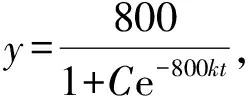
2 结束语

微分方程是研究自然科学、工程技术及社会生活现象的重要工具.通过研究微分方程解的各种属性，能够解释一些现象，对未来的发展趋势做出预测，为人们设计的新装置提供参考.微分方程为自动控制设计、气象数值预报、人口增长宏观预测等提供了重要的理论依据[4].本文仅选取微分方程中的部分内容，将数学建模思想融入常微分方程教学中，把数学与实际生活紧密联系在一起.在教学过程中采取“案例式教学”，案例的分析采用“提出问题——问题分析——模型建立——模型求解”的教学模式，向学生讲清微分方程的实际背景，列出微分方程并进行求解，再返回到实际问题中去解释生活中的实际现象.这样，既提高了学生的学习兴趣，又增强了学生的学习能力，通过案例教学的开展，学生学习数学的积极性有了较大幅度的提高，也对数学建模有了更深的认识，这种新型教学模式值得我们在教学过程中长期坚持.

[1] 李薇,李卫军,戴明强.将建模思想融入数学教学,培养大学生数学素质[J].湖北师范学院学报：自然科学版,2009,29(3):108-111.

[2] 熊佐亮, 蒋鹏, 朱向洪,等.微分方程应用若干举例[J].江西教育学院学报，2006,(12):1-3.

[3] 王宪杰，候仁民，赵旭强.高等数学典型应用实例与模型[M].北京：科学出版社，2006:57-58.

[4] 陈代进.案例教学在高职计算机网络基础理论教学中的实践探索[J].计算机教学与教育信息化，2009,23(4)：1 083-1 084.

Analysis on Cases of Mathematical Modeling in Ordinary Differential Equations

LIU Hongxia， ZHOU Shaowei

(CollegeofMathematicsandSystemScience，ShandongUniversityofScienceandTechnology，Qingdao266590，China)

In the teaching of differential equation, the issues related to practical life are selected and solved by adopting the idea of mathematical modeling. The case teaching helps the student to integrate theory with practice, and grasp the theory of ordinary differential equations better.

ordinary differential equations; mathematical modeling; actual case

2015-06-18

山东科技大学教育教学研究“群星计划”项目(QX2013265)；山东科技大学教学研究项目(JG201504)

刘洪霞(1979—)，女，山东泰安人，山东科技大学数学与系统科学学院讲师.

10.3969/j.issn.1007-0834.2015.04.018

O13;G642.0

A

1007-0834(2015)04-0065-03