电力无线传感器网络中不良数据的检测与修正

甄倩倩， 王丁磊

(安阳师范学院 软件学院，河南 安阳 455000)

电力无线传感器网络中不良数据的检测与修正

甄倩倩， 王丁磊

(安阳师范学院 软件学院，河南 安阳 455000)

为检测无线传感器网络中的不良数据并对其修正，提出了一种新的不良数据检测与修正方法.该方法利用空间相关性以及先验数据建立一个数学模型，然后给出一定的偏离度范围.如果检验数据的偏离度在给定的偏离度范围内，则该数据为正常数据，反之，该数据为不良数据.在数据集上多次测试结果表明，该算法能够对不良数据进行检测与辨识，并给出了相对精确的估计值.

无线传感器网络；空间相关性；不良数据；检测与修正；偏离度

0 引言

在电力系统无线传感器网络采集、传输、存储等过程中,由于工况复杂，数据在收集过程中可能产生各种噪声、离群点或较大的误差[1]，如果测量值与真实值之间偏差较大，则该数据即可称为不良数据.电力系统运营中包含很多数据，这些数据是否准确将直接影响电力系统的运行安全，因为无线传感器的自身特点以及其部署区域的外部环境造成不良数据的出现在电力系统的日常运营中是不可避免的.如果不对其进行处理，那么它的存在有时会使电力调度人员对电力系统的状态估计不清，从而影响电力系统的正常运营以及安全.所以不良数据检测与辨识是电力系统状态估计的重要功能之一，其功能是发现和排除测量采样数据中偶然出现的少数不良数据，以提高状态估计的可靠性[2].电力系统中不良数据检测与修正对状态估计结果的准确性起着重要作用[3].电力系统不良数据检测与修正能够避免一些错误数据的出现，减少误差，从而在一定程度上提高在线或离线计算程序的可信度[4].基于以上原因提出了一种不良数据检测并修正的算法，用于修正电力系统中存在的不良数据，从而提高数据系统的可靠性.

1 相关工作

近年来，许多学者以数学、控制理论和其他新理论为指导，进行电力系统不良数据检测与辨识问题的研究，并结合电力系统的特点，在理论研究与工程应用方面取得了大量的成果，进一步丰富和发展了相关算法[5]，并提出很多与之相关的算法，例如基于k-means聚类算法[3]、基于模糊数学理论[5]、基于残差信息辨识的不良数据[6]、新息图[7]、基于模糊聚类[8]、基于小波的[9-10]、基于最大指数绝对值目标函数[11]、基于神经网络的以及基于模式匹配的不良数据检测方法等.

文献[3]对具体的应用背景提出了相应的不良数据辨识方法，主要研究日负荷曲线中的不良数据，提出了一种基于改进的k-means聚类算法，该算法首先结合有效指数准则，提取出电力系统中的日负荷曲线，并利用提取出的负荷曲线对待检测曲线进行检测与辨识，最终确定出待检测曲线中是否含有不良数据.文献[5]提出了一种基于模糊数学理论的综合评价算法，并根据算法建立隶属度函数以及评价指标，并对不同的算法进行评价，比较各个算法的优缺点.文献[6]提出了一种解决多不良数据辨识的方法，该方法不存在残差污染和残差淹没的问题.该方法首先选取部分数据进行估计，然后用剩余的数据替换掉参与估计的待检测数据，并计算替换后的各个数据的标准化残差的大小对数据进行评估，从而辨别出不良数据.文献[7]提出了一种新息图法，该方法寻找新息偏大的可疑的节点并寻找该节点是否存在突变路径，从而最终确定突变子网存在与否，进而识别不良数据.文献[8]在模糊集理论的基础上提出的一种检测方法，该方法将相邻的两个采样时刻的数据差以及标准残差作为特征对象进行模糊聚类分析，根据已知的优良数据，辨别出其他优良数据，从而最终检测出变异的不良数据.文献[9]使用傅里叶函数变换以及小波分析法对不良数据进行检测.文献[10]利用小波自身的去除噪声的原理以及其奇异性检测理论，提出了一种对不良数据进行辨识的新方法.该算法能够确定不良数据的类型及位置.文献[11]中提出了一种用最大指数绝对值来衡量数据是不是不良数据，通过引进辅助变量得到等价模型，并进行求解，该算法可以抑制多个强相关的不良数据.

但上述所列举的这些算法都没有考虑到无线传感器的特性，所以无法应用在无线传感器网络的不良数据辨识上.无线传感器网络某些节点之间空间上具有很大的相关性，以及节点本身时间序列的特性，所以本文针对特定的用处选择了充分考虑无线传感器网络的空间相关性的算法对不良数据进行检测与修正.

2 基于空间相关性和偏离度的不良数据检测与修正算法

2.1 相关定义

定义1 偏离度(degree of deviation)：偏离度是指真实数据偏离目标数据的程度.

偏离度计算公式如式(1)所示，

(1)

其中dev:偏离度，abs:绝对值，real:真实数据，target:目标数据.

定义2 相似性度量(similarity measurement)：相似性度量是用于比较一些形状、图像、信息或数据相似性的一个函数[12].

文献[12]中比较了几种不同的相似性度量，例如，积相关、绝对差、平方差、平均绝对差、平均平方差、归一化积等.另外，在数据挖掘中还有一些常用的衡量相似性的函数，常用的相似性函数有欧氏距离.但欧氏距离等计算虽然简单，却不能处理不等长序列，在两个序列完全相似而只是沿y轴移动一段距离的情况下会出现错误的判别，而且它们并不能反映两个序列相似性的本质[13].文献[14]提出了一种斜率相似性度量.基于斜率的时间序列相似性度量方法在线性分段的基础上，对两个序列间的斜率差进行加权[14].选择不同的相似性度量函数对最后的结果会产生很大的影响，所以选择一个合适的相似性度量函数相当重要.为了选择一个合适的相似性度量函数，结合无线传感器的具体特性进行考虑，即用空间上的相关性来度量节点之间的相似性.对于某一个实测节点来说，由于无线传感器之间的空间相关性，在数据质量正常的情况下，节点之间会有近似的函数对应关系.

2.2 算法描述

对于正常的电力系统运营过程中的数据，都在固定的范围内波动，不会有很大的偏差，所以基于这一原理，本文在有先验经验的基础上,利用历史的正常数据先建立数学模型，然后对数据进行判定.具体过程如下：

1)求皮尔逊相关系数，选取相关性大于0.3的节点.任意节点i与j之间的皮尔逊相关系数计算为

(2)

其中，j=1,2,…,i-1,i+1,…,n.yik代表节点i的第k个值，yjk代表节点j的第k个值.yi代表节点i的平均值，yj代表节点j的平均值.r(i,j)∈[-1,1]，用以反映两个变量之间关系密切程度的统计指标.

2)建模.根据参与建模的节点用最小二乘法按照公式(3)构造多元回归分析函数，给每一个节点建立一个拟合模型,其中k为相关变量的数目，Xk为第k个变量，βj(j=1,2,…,k)称为回归系数.

Yi=β0+β1X1+β2X2+β3X3+…+βkXk.

(3)

3)利用模型预测并判定不良数据.判定某一节点中检测序列数据点是不是不良数据.首先根据建立的模型求出检测数据点的预测值，然后根据预测值与检测值求出偏离度，如果偏离度在正常偏离度的范围内，则该数据为正常数据，继续对下一个值进行判定，反之，该数据为不良数据，用预测模型得到的值替换检测值，继续对下一个值进行检测.

3 实验结果及分析

本文在MATLAB R2012b下进行仿真实验，数据采用电力系统运营过程中由6个传感器采集到的真实完整且数据质量良好的空气预热器烟气出口温度数据集(如图1所示).为了验证算法的有效性与精确性，对数据集进行一定的修改，使得数据集中含有一定的不良数据，使用算法对其进行辨识，检验算法是否能够识别，并检验修正后的值与真实值之间的误差范围.

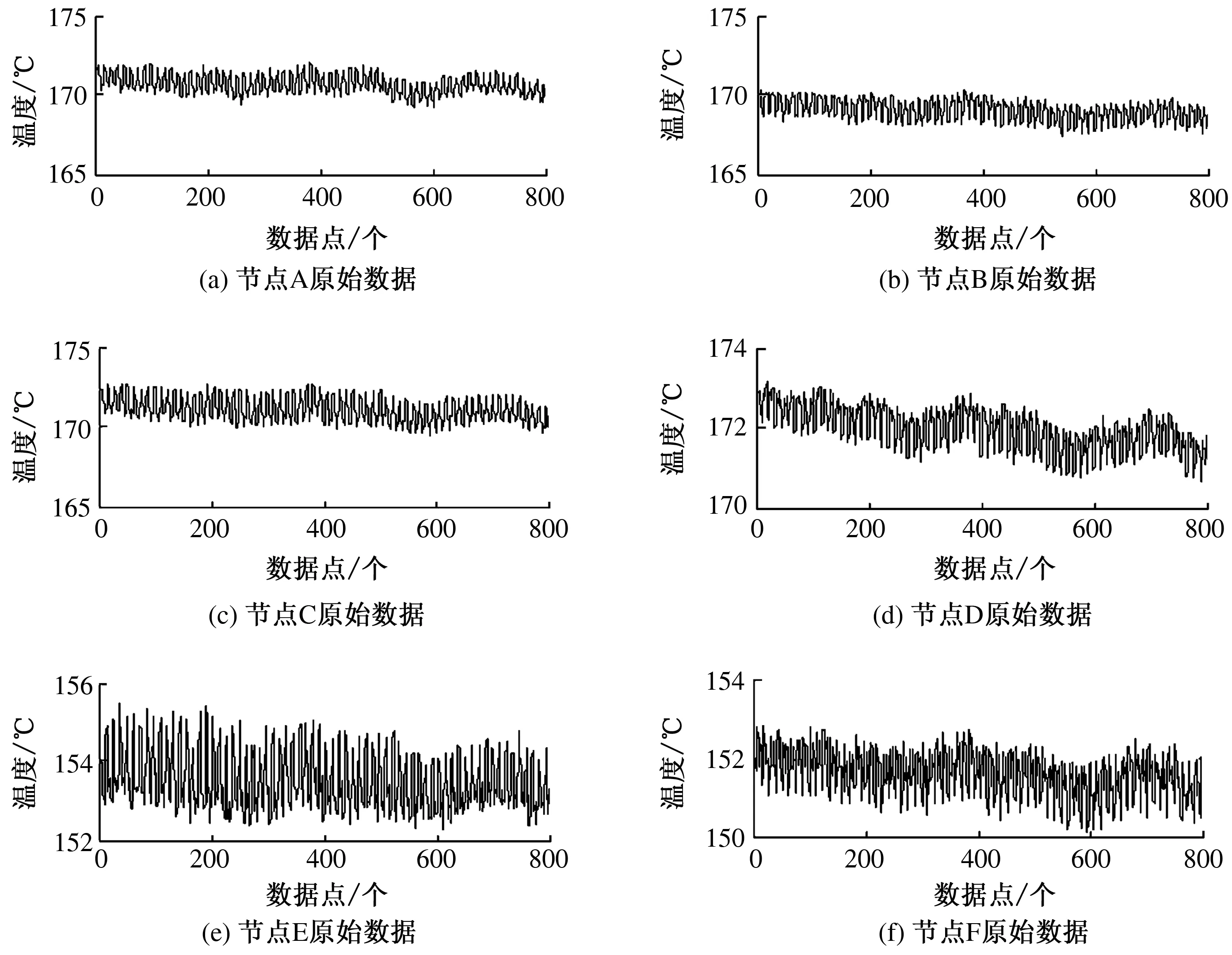
图1 原始数据Fig.1 Raw Data

3.1 实验设定

实验选用的是6个温度传感器采集到的空气预热器出口温度值，分别命名为节点A、节点B、节点C、节点D、节点E、节点F.图1是这6个节点所采集到的800个数据的详细信息.由图1可知，一段时间内，数据固定在一定的范围内波动,所以为了检测不良数据，选取前400个正常数据点作为训练样本建立数学模型，并求出误差范围的大小.

为了验证数据的有效性，可以进行以下两种假设条件实验：

(1)假设节点A的第500和第600个节点是不良数据，原数据值分别为169.997,171.385，将它们分别修改为168.997,172.385，即为第500个数据减少了1 ℃，第600个数据增加了1 ℃，并分析设定偏离度的大小对实验结果的影响.

(2)假设节点A的第601到第650个数据以步长0.1 ℃的方式递减，即601个数据减少了0.1 ℃,602个数据减少了0.2 ℃,第603个数据减少了0.3 ℃，依次类推，并分析设定偏离度的大小对实验结果的影响.

3.2 实验结果分析

通过求解相关系数，得出节点A与节点B、C、D、E、F的相关系数分别为0.705 9、0.965 9、0.727 6、0.240 4、0.020 2.如果节点与节点A的相关性大于0.3，则将其加入参与回归分析的队列中，故节点B、C、D参与回归分析，得到线性回归分析模型为dataA=26.153 8-0.091 9×dataB+0.809×dataC+0.125 8×dataD，其中dataA、dataB、dataC、dataD分别代表节点A、B、C、D的数值.根据上述拟合模型求得的预测值与真实值之间的误差范围为[-0.401 8, 0.378 9],误差绝对值的平均值为0.104 1，预测序列的平均值为171.086 8.

首先实验设定(1)，根据建立的多元线性回归模型，依次求得节点A第401到800的预测值，并将其与真实值之间的误差进行对比.

根据偏离度的定义可知，第401到第800个数据的偏离度情况如图2所示.

根据偏离度在设定范围内为正常数据，反之则为不良数据的概念，由图2可以明显分析出如果偏离度的设定范围在0.2%以内，那么很多正常点都被识别为不良数据，如果偏离度设定在0.3%以内，那么会有两个点有误，如果偏离度范围设定在0.4%以内，则正好能够检出这两个不良数据.即第500个和第600个数据不在正常偏离度的范围内(分别为0.687 8和0.567 3)，而其他值都在正常偏离度的范围内，所以可以把它们识别为不良数据，使用预测的数据值代替原始数据，从而可以达到修正不良数据的目的，它们的预测值分别为170.167 3、171.412 6，与修改前的数据误差都很小，与实验前的真实值基本吻合.

实验设定(2)中，依旧根据已经求出来的多元线性回归模型对第401到第800个数据点依次进行判定，已经建立的数学模型为：dataA=26.153 8-0.091 9×dataB+0.809×dataC+0.125 8×dataD.求出的预测序列与实验设定(1)中所求的相同，因为参与计算的其他节点值没有改变，都是正常值.实验设定(2)检测序列的偏离度如图3所示.

图2 检测序列的偏离度Fig.2 Deviation of detection sequence

图3 检测序列的偏离度Fig.3 Deviation of detection sequence

图4 预测值与原始真实值之间的对比Fig.4 The comparison of predicted value and real value

由图3可知，第600到第650个数据点数据远远偏离正常的偏离度范围.实验结果表明，如果偏离度的范围设定在0.2%以内，会有很多数据被检测为不良数据，如果偏离度的范围设定在0.3%以内，仍然会有部分数据被误检，而偏离度如果设定在0.4%以内，则刚好能够检测出第606到第650个数据点.因为从第606个数据开始偏离度大于0.4%，所以在本实验中该算法能够检测出与真实值误差大于0.8的不良数据.所以从第606个数据到第650个数据均被检测出来，并用预测值对其进行修正，具体的预测值与原始真实值之间的对比图如图4所示.

由图4所示，预测值与原始真实值序列基本重合，它们之间误差很小，可以忽略，所以可以使用预测值来对不良数据进行修正.这样的值很接近真实值，对电力系统中的决策具备良好的参考价值.

综合两个实验分析可知，偏离度设定在0.4%，刚好能够检测出不良数据，而又不至于将正常数据误辨识为不良数据，所以偏离度设定在0.4%比较合理.

4 结论

本文针对电力系统运营中无线传感器网络中存在不良数据的问题，提出了一种基于空间相关性以及偏离度的不良数据检测方法，并对不良数据进行数据修正.通过多次比对实验得到了一个最合理的偏离度的取值，最后在真实数据集上进行仿真分析，实验结果表明，该算法能够检测出系统中存在的不良数据，且不会产生误检的情况，对于不良数据修正后的结果接近真实值.本文提出的算法估计精度高，精确的数据为数据分析等进一步工作奠定了良好的基础，从而使得电力人员能够正确评估设备等的运营情况并能够及时做出调整.

[1] 黎灿兵,刘晓光,赵弘俊,等.中压配电网不良负载数据分析与处理方法[J].电力系统自动化，2008,32(20):97-99.

[2] 刘莉,翟登辉,姜新丽.电力系统不良数据检测与辨识方法的现状与发展[J].电力系统保护与控制,2010,38(5):143-147.

[3] 刘莉,王刚,翟登辉.k-means聚类算法在负荷曲线分类中的应用[J].电力系统保护与控制,2011,39(23):65-68.

[4] 王兴志, 严正, 沈沉, 等. 基于在线核学习的电网不良数据检测与辨识方法[J].电力系统保护与控制, 2012, 40(1): 50-55.

[5] 蒋德珑,王克文.不良数据检测与辨识算法的评估研究[J].计算机工程与应用, 2012,48(22) :239-243.

[6] 卢志刚,张宗伟.基于量测量替换与标准化残差检测的不良数据辨识[J].电力系统自动化,2007,31(13):52-56.

[7] 毛志强，蔡中勤，周苏荃，等.基于新息图法的电力系统负荷突变辨识[J].电力系统自动化,2011,35(12):37-41.

[8] 蒋德珑,王克文,王祥东.基于模糊等价矩阵聚类分析的不良数据辨识[J].电力系统保护与控制,2011,39(21):1-6.

[9] 康仁.基于小波分析的母线负荷预测不良数据检测[J].中国电力,2011,44(8):5-8.

[10]李慧,杨明皓.小波分析在电力系统不良数据辨识中的应用[J].继电器,2005,33(3):10-14.

[11]付艳兰,陈艳波,姚锐,等.基于最大指数绝对值目标函数的抗差状态估计方法[J].电网技术,2013,37(11):3 166-3 171.

[12]刘宝生,闫莉萍,周东华.几种经典相似性度量的比较研究[J].计算机应用研究, 2006, 23(11): 1-3.

[13]汤胤.时间序列相似性分析方法研究[J].计算机工程与应用,2006,42(1):68-71.

[14]张建业,潘泉,张鹏,等. 基于斜率表示的时间序列相似性度量方法[J].模式识别与人工智能, 2007, 20(2): 271-274.

Detection and Correction of Bad Data in Wireless Sensor Network of Power System

ZHEN Qianqian, WANG Dinglei

(SchoolofSoftwareEngineering,AnyangNormalUniversity,Anyang455000,China)

In order to detect and amend the bad data in wireless sensor network, a new bad data detection and correction algorithm is proposed. The proposed algorithm uses prior data bank and spatial correlation of wireless sensor network, and it gives the range of deviation. If the detected data in a certain deviation of given range, the data are normal data, otherwise, bad data. The test results on the data sets show that the proposed algorithm is able to detect and identify bad data and give bad data an estimated value.

wireless sensor network; spatial correlation; bad data; detection and correction; degree of deviation

2015-07-15

甄倩倩(1988—)，女，河南开封人，安阳师范学院软件学院教师.

10.3969/j.issn.1007-0834.2015.04.011

TP391

A

1007-0834(2015)04-0038-05