连续型L′Hospital法则与离散型Stolz定理的关联性探讨
2015-03-24刘志红
刘志红
(郑州财经学院 计算机系,河南 郑州 450044)
连续型L′Hospital法则与离散型Stolz定理的关联性探讨
刘志红
(郑州财经学院 计算机系,河南 郑州 450044)
通对Stolz定理和L′Hospital法则的推导证明,有效架起了Stolz定理和L′Hospital法则联系的桥梁,使之相互融会贯通,将应用Stolz定理和L′Hospital法则一体化.通过一些实例的应用,进一步探索这两个重要工具的内涵性和广延性.
Stolz定理; L′Hospital法则;未定式;推广形式;中值定理
0 引言
1 理论储备
1.1 Stolz定理[1]

1.2 L′Hospital法则
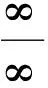


(2)在点a附近(x≠a),f′(x)和g′(x)都存在,并且g′(x)≠0;

注记1 定理对于无限变化过程x→a+和x→a-都是适用的.

2 中心桥梁——Stolz定理的推广形式


(1)g(x+T)>g(x),x∈[a,+∞);



(1)0 3.1 利用推广定理证明Stolz定理 证明如下: 作g(x)=bn,x∈[n,n+1),f(x)=an,x∈[n,n+1). 取T=1,则显然 (1)g(x+1)>g(x); 于是由推广定理,有 从而 证明如下: 只须验证f(x)及g(x)在[a,+∞)上满足推广定理条件即可. 这里T=1,首先g′(x)≠0,x∈[a,+∞).由达布定理,知g′(x)在[a,+∞)内不变号. 下面验证条件: (1)由Lagrange公式,∀x∈[a,+∞)有θx∈(0,1)使 g(x+1)-g(x)=g′(x+θx),x∈[a,+∞),g′(x+θx)>0, 所以,g(x+1)-g(x)>0,即g(x+1)>g(x)[4]; (2)由条件f(x)可导,故f(x)在[a,+∞)的任意子区间上有界,g(x)=+∞已由条件直接给出; 由(1)、(2)和(3),并由L′Hospital法则假设条件推得f(x)及g(x)满足条件. [1] 刘泽庆.数学分析中的典型例题和例题选讲[M].大连:大连海事出版社,1987:127-135. [2] 菲赫金哥尔茨 T M.微积分教程[M].北京:人民教育出版社,1956:87-101. [3] 陈伟侯,翟连林,段云鑫.微积分基础:上册[M].北京:科学出版社,1984:92-98 [4] 孙本旺,汪浩.数学分析中的典型例题和解题方法[M].长沙:湖南科学出版社,1981:165-174. Discussion on Connection Between L′Hospital Rule of Continuous Type and Stolz Theorem of Abstract Type LIU Zhihong (DepartmentofComputerScience,ZhengzhouInstituteofFinanceandEconomics,Zhengzhou450044,China) By the derivation of Stolz Theorem and L′Hospital Rule, the connection of Stolz Theorem and the law of L′Hospital are given. The integration of Stolz Theorem and L′Hospital Rule will apply. Through some examples of the application, the connotation and the wide ductility of these two important tools are further explored. Theorem of Stolz; Rule of L′Hospital; undecided type; promotion form; mean value theorem 2015-07-10 河南省高等学校重点科研项目计划 (15B110010) 刘志红(1983—),男,河北邯郸人,郑州财经学院计算机系讲师. 10.3969/j.issn.1007-0834.2015.04.002 O172 A 1007-0834(2015)04-0007-03

3 中心桥梁的辐射应用
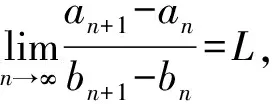






4 结语
