摆镜平台寿命的Bootstrap估计*
2015-03-24王景宇戴妍峰
王景宇,戴妍峰
(1. 中国科学院国家天文台,北京 100012;2. 中国科学院太阳活动重点实验室 (国家天文台),北京 100012)
摆镜平台寿命的Bootstrap估计*
王景宇1,2,戴妍峰1,2
(1. 中国科学院国家天文台,北京 100012;2. 中国科学院太阳活动重点实验室 (国家天文台),北京 100012)
摆镜平台是大口径空间天文望远镜图像稳定控制系统中的一个活动部件,为评估其寿命,进行了摆镜平台寿命试验。摆镜平台寿命试验为单子样寿命试验,先验概率信息很少,采用Bayes方法进行寿命估计有一定的困难。Bootstrap方法是一种非参数统计方法,它对未知分布不做任何假设,仅利用计算机对原始样本数据进行再抽样模拟未知分布,通过再生抽样将小样本问题转化成大样本问题。Bootstrap方法要求子样数要大于等于5。采用半经验虚拟增广子样和Bootstrap相结合的方法进行摆镜平台寿命的区间估计。在摆镜平台寿命服从威布尔(Weibull)分布的假定下,通过以往类似产品寿命试验数据推断出威布尔分布形状参数,然后用寿命试验值和威布尔分布形状参数推导出摆镜平台寿命的方差,在此基础上进行子样虚拟增广。虚拟增广子样需要满足两个条件:(1)增广子样的均值等于寿命试验值;(2)虚拟增广子样的方差等于类似产品寿命的经验方差。根据这两个条件建立一个方程组,用数值计算法求解方程组得到增广子样。这些作为Bootstrap区间估计原始样本的增广子样用于计算样本的经验分布和样本重抽样。通过重抽样得到10 000个样本,计算每个样本的均值,然后对10 000个均值进行排序,得到均值μ1≤μ2≤…≤μ10 000,采用分位数法计算置信水平为1-α的Bootstrap置信区间,得到置信区间(μk1,μk2),其中k1=[10 000 ×α/2],
摆镜平台;Bootstrap方法;增广子样;Weibull分布;置信下限
摆镜平台是空间太阳望远镜图像稳定控制系统中的一个部件,为研究摆镜平台在空间环境下的使用寿命,国家天文台建立了摆镜平台寿命试验系统,并在此系统上进行了摆镜平台寿命试验。由于摆镜平台是一种高可靠性且价格昂贵的产品,因此,在进行寿命试验时只采用一个摆镜平台作为试件。在这种情况下,摆镜平台寿命评估属于单子样寿命试验评估问题。通常处理小子样估计的方法有Bayes方法和Bootstrap方法[1-2]。由于摆镜平台的验前信息极少,采用Bayes方法进行寿命评估有一定的困难。Bootstrap方法是一种非参数统计方法,它对未知分布不做任何假设,仅利用计算机对原始样本数据进行再抽样模拟未知分布,通过再生抽样将小样本问题转化成大样本问题[3]。Bootstrap方法要求子样数n≥5,为使用Bootstrap方法对摆镜平台寿命进行评估,采用文[2]中的方法对子样数进行虚拟扩展,将子样数由1增加到5以上,然后再利用Bootstrap方法进行摆镜平台寿命估计,给出摆镜平台平均寿命的置信区间和置信下限。
1 半经验虚拟增广子样与Bootstrap方法相结合的极小子样评估方法
文[2]给出了极小子样试验的半经验评估方法,同时指出这种评估方法由于试验均值的标准差大导致置信下限下降很大。为克服这一缺点,文[2]的作者提出了一种半经验虚拟增广子样与Bootstrap方法相结合的极小子样评估方法。
1.1 半经验虚拟增广子样方法
为使虚拟增广新子样所蕴含的随机特性与原子样随机性的差别在允许范围之内,虚拟增广子样应满足下列条件:
(1)虚拟增广后的子样均值应与原来的子样均值相等;
(2)虚拟增广后的子样标准差与类似件的子样标准差相等。
具体增广方法如下:设T0为试验值,σ为半经验所得的试验值的标准差,由于试验中试件只有一个,只得到一个试验值T0,因此,只能以此试验值作为试验均值的估计值。虚拟增广子样为Ti,i=1,2,…,n,其中某一子样值为T0,满足下列方程组:
.
(1)
采用数值计算的方法解上述方程组得到虚拟增广子样。
1.2Bootstrap方法
Bootstrap方法是美国Stanford大学教授Efron于1979年提出的一种新的统计推断方法,是一种只依赖于给定观测信息,而不需要其它假设的统计推断方法。
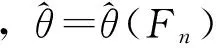
≜Tn,
由观测X=(x1,x2, …,xn)估计R(X,F)分布特征的基本步骤如下[3]:

.
(2)
(2)从Fn中抽取子样
X*
X*称为Bootstrap子样。
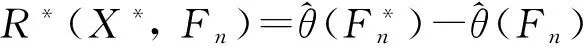
利用Rn的分布模拟Tn的分布,可以对分布参数θ进行区间估计。
1.3 单子样寿命试验的区间估计
利用半经验虚拟增广子样与Bootstrap方法相结合的极小子样评估方法可进行单子样寿命试验的区间估计,具体步骤如下:
(1)利用虚拟增广方法将子样由1个增广到n个;
(2)将n个子样值按从小到大顺序排列,然后计算经验分布函数Fn;
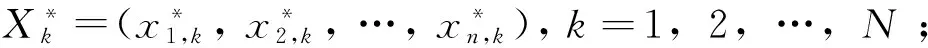
(4)利用上述抽样集合计算寿命的Bootstrap置信区间[4]。
1.4 算例
文[2]给出了一个用此方法估计飞行器结构寿命的算例:一飞行器结构做了一次寿命试验,得出其寿命为T0=20 000 h,由经验知其寿命为对数正态分布,对数寿命的标准差σY=0.17,其中Y=logT,利用(1)式将Y由1个Y0=logT0=4.301,虚拟增广到5个{3.801,4.105,4.301,4.497,4.801},再用Bootstrap方法求出均值估计密度分布,得到Y均值90%置信度下限为4.084 76,对应寿命T均值的置信下限为12 153 h。
2 摆镜平台寿命估计
2.1 摆镜平台寿命的分布
威布尔(Weibull)分布是瑞典物理学家Weibull在分析材料强度时推导的一种概率分布类型。由于威布尔分布含有两个或三个参数,它对各种类型试验数据拟合的能力强,因此,使用广泛,许多随机现象可认为近似服从威布尔分布。

(3)
式中,ηi为各部件分布的比例参数。
寿命试验中的试件为德国PI公司的S-340型摆镜平台,由两对压电陶瓷触动器推动摆镜平台台面摆动,S-340摆镜平台中的压电陶瓷促动器为PI公司的PICMA(PICeramicco-firedmultilayeractuators),根据文[5]PICMA的寿命服从两参数威布尔分布,形状参数m的平均值为1.4。通过对摆镜平台构成部件的分析,认为摆镜平台寿命主要由PICMA决定。由于摆镜平台中两对PICMA的使用环境和工作条件相同,因此,可以认为其寿命分布的形状参数相同。假定摆镜平台的寿命为最薄弱的一个PICMA的寿命,根据(3)式摆镜平台寿命分布也为威布尔分布,且形状参数与PICMA相同为1.4。
2.2 单子样摆镜平台寿命试验的寿命Bootstrap置信下限计算
文[6]给出了寿命服从威布尔分布情况下的半经验虚拟增广子样与Bootstrap结合的方法,将子样数由1虚拟增广到7,用Bootstrap方法计算平均寿命的置信下限。用此方法计算摆镜平台平均寿命置信下限的过程如下:
摆镜平台寿命T服从两参数威布尔分布,概率密度函数为
(4)
式中,m为形状参数;η为比例参数。摆镜平台寿命T的均值、方差用Γ函数表示为
(5)
(6)
设T0为摆镜平台寿命的试验值,根据威布尔分布将其虚拟扩展为7个子样,记为T1、T2、T3、T4、T5、T6、T7,由于威布尔分布密度函数是偏态的,因此,在进行虚拟子样扩展时,在试验值T0左边取4个点,右边取2个点,且满足T1 (7) 化简后为 . (8) 因为只有一个试验值T0,只能将它作为试验值均值的估值,即E(T)≈T0,由(5)、(6)式及m=1.4得D(T) (9) 将(9)式代入(8)式得 (10) 令Ti=kiT0,i=1, 2, 3, 4, 6, 7代入(10)式得 (11) 利用数值计算方法解(11)式,可给出ki,i=1,2,3,4,6,7,由此得到扩展子样X: X=(k1T0,k2T0,k3T0,k4T0,T0,k6T0,k7T0), 利用X计算摆镜平台平均寿命的Bootstrap置信区间,具体步骤如下: 为加快寿命试验的进程,在寿命试验中引入了加速过程,目前加速因子为5.5。摆镜平台寿命试验从2013年1月1日开始,到2014年3月18日已进行442天,摆镜平台工作正常。因此,可以认为寿命试验值T0=442×24×5.5=58 344 h,h表示小时。利用(11)式选出一组系数ki,i=1,2,3,4,6,7 与T0相乘得到的增广子样为 单位为h。取N=10 000,按上述Bootstrap置信区间的方法用Matlab编程计算,得到摆镜平台寿命90%、95%、98%和99%的Bootstrap置信区间,具体值见表1。 如果摆镜正常工作2年,寿命试验值T0=730×24×5.5=96 360 h,摆镜平台寿命90%、95%、98%和99%的Bootstrap置信区间计算结果见表2。 表1 摆镜平台正常工作442天情况下寿命 Bootstrap置信区间计算结果 Table 1 Confidence intervals for the lifetime of the tip-tilt platform at the time when it has been working normally for 442 days as calculated using our bootstrap method 置信度/%置信下限/h置信上限/h903576684146953146889163982859896688992680899916 表2 摆镜平台正常工作2年情况下寿命 Bootstrap置信区间计算结果 Table 2 Confidence intervals for the lifetime of the tip-tilt platform at the time when it has been working normally for 2 years as calculated using our bootstrap method 置信度/%置信下限/h置信上限/h9057889138975955197114726098466451573249944277163833 从表1可知95%置信区间为[31 468 h,89 163 h],或[3.59年, 10.18年],置信下限为T0.95=31 468h=3.59年。 从表2可知95%置信区间为[51 971h,147 260h],或[5.93年, 16.81年],置信下限为T0.95=51 971h=5.93年。 对单子样摆镜平台寿命试验,在摆镜平台近似服从威布尔分布的假定下,根据以往摆镜平台组件寿命试验数据推断威布尔分布的形状参数,在此基础上可以采用半经验虚拟增广子样与Bootstrap方法相结合的方法进行摆镜平台寿命的Bootstrap区间估计,给出摆镜平台寿命的置信区间和置信下限。 [1] 冯蕴雯, 冯元生. 极小子样高可靠性成败型产品试验的贝叶斯评估方法研究[J]. 机械科学与技术, 1999, 18(2): 198-200.FengYunwen,FengYuansheng.StudyofBayes’estimationforproducttestofextremesmall-samplehigh-reliabilitysafe-or-failurepattern[J].MechanicalScienceandTechnologyforAerospaceEngineering, 1999, 18(2): 198-200. [2] 冯蕴雯, 黄玮, 吕震宙, 等. 极小子样试验的半经验评估方法[J]. 航空学报, 2004, 25(5): 456-459.FengYunwen,HuangWei,LvZhenzhou,etal.Thesemiempiricalevaluationmethodforextremesmallsampletest[J].ActaAeronauticaEtAstronauticaSinica, 2004, 25(5): 456-459. [3] 唐雪梅, 张金槐, 邵凤昌, 等. 武器装备小子样试验分析与评估[M]. 北京: 国防工业出版社, 2001. [4] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京: 高等教育出版社, 2008. [5]PertschP,BroichB,BlockR,etal.DevelopmentofhighlyreliablepiezomultilayeractuatorsandlifetimetestunderDCandACoperatingconditions[EB/OL]. 2010[2013-12-18].http://www.piezo.ws/pdf/Development_Highly_Reliable_Piezo_Actuators_white_Paper_PI_Ceramic.pdf. [6] 杨海峰, 冯蕴雯, 冯元生. 单子样结构疲劳试验寿命评估方法研究[J]. 机械设计与制造, 2010(9): 109-111.YangHaifeng,FengYunwen,FengYuansheng.Researchonreliabilityassessmentofsinglesample[J].MachineryDesign&Manufacture, 2010(9): 109-111. CN 53-1189/P ISSN 1672-7673 Estimation of the Lifetime of a Tip-Tilt Platform Using a Bootstrap Method Wang Jingyu1,2, Dai Yanfeng1,2 (1. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China,Email: wangjingyu@bao.ac.cn; 2. Key Laboratory of Solar Activities, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China) Tip-Tilt Platforms; Bootstrap method; Augmented sample; Weibull distribution; Lower confidence bound 国家自然科学基金 (11078018) 资助. 2014-03-18;修定日期:2014-04-24 王景宇,男,研究员. 研究方向:天文仪器与方法. Email: wangjingyu@bao.ac.cn TP273 A 1672-7673(2015)01-0096-06 上述方法计算0.95置信水平的Bootstrap置信下限为3.59年,如果正常工作两年,0.95置信水平的Bootstrap置信区间为(5.93年,16.81年)。
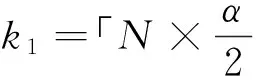

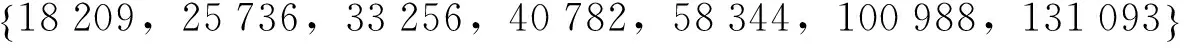


3 结 论


