基于反射信号提取的双星系统轨道估算*

高 扬, 周建锋

(1. 清华大学工程物理系天体物理中心，北京 100084; 2. 粒子技术与辐射成像教育部重点实验室 (清华大学)，北京 100084)

基于反射信号提取的双星系统轨道估算*

高 扬1,2, 周建锋1,2

(1. 清华大学工程物理系天体物理中心，北京 100084; 2. 粒子技术与辐射成像教育部重点实验室 (清华大学)，北京 100084)

在观测双星系统时，接收的信号包含伴星反射成分。反射信号的时延可以给出伴星的位置、运动等信息，提取反射信号可以实现双星系统的轨道估算。利用相关函数，可实现对反射信号的提取，但由于双星的相对运动，直接对接收信号进行自相关运算不能提取反射信号。提出了一种基于对接收信号在时域做变换的方法，计算接收信号与变换后信号的互相关函数，可以解决运动情形下反射信号的提取。利用MATLAB对具体的情形进行了模拟，成功地提取了反射信号，验证了该方法的有效性。

双星；时延估计；相关函数；参数空间

天体发射源周围存在反射介质，因此观测得到的信号中会有反射成分。利用相应的方法，分析反射成分可以获得超新星遗迹的前身星、活动星系核(Active Galactic Nuclei, AGN)核心黑洞的质量等重要信息。

反射信号与发射信号之间有一定的时间延迟，利用时延可以研究反射介质的相对位置、速度等参数及相关信息。例如，可以利用回光现象确定超新星前身星。超新星爆发时周围若存在大量的尘埃，其爆发时发出的光线抵达尘埃所在的地方，尘埃会散射光线，同时尘埃会吸收超新星的光线，并以不同的波长辐射，即是超新星的回光现象[1]。回光到达地球的时间较爆发的时间有延迟，但可以保存爆发时与光线有关的信息，利用回光分析可确定超新星遗迹周围星际介质的分布、超新星遗迹的年龄及距离等信息，并且可以获得超新星爆发时的光谱以确定超新星的类型[2]。通过观测回光，文[3]证实了Cassiopeia A Supernova是来自红超巨星氦核坍缩的IIb型超新星。观测到第谷超新星的436年后，Krause等人观测到其回光，并获得回光图像与光谱，确定了第谷超新星为正常Ia型超新星[4]。由于回光现象较超新星爆发信号有延迟，因此利用回光现象可以进行距离的测定及光谱分析，对超新星的诸多细节进行研究，例如确定前身星、测量尘埃环的半径等[5]。

信号处理中，利用相关函数可以有效地检测带有噪声的信号，以及信号的周期性，测量信号的时延长度。在提取反射信号与发射信号间的延迟信息时，相关函数是常用的方法[6]。

天体物理中，在测量活动星系核核心黑洞质量时所用到的反响映射(Reverberation Mapping)原理，就是利用信号的相关函数检测时延长度，通过时延长度确定宽线区(Broad-Line Region, BLR)与核心的距离，利用这一距离可以确定活动星系核核心黑洞的质量[7]。

在活动星系核统一模型中，核心有由吸积驱动的超大质量黑洞，吸积盘的外侧是宽线区，核心黑洞的连续辐射传播到宽线区，由于光致电离效应，此处的尘埃会受激产生发射线，同时，宽线区的尘埃会绕黑洞旋转，因此发射线会有多普勒展宽，利用维里定理和宽线区的谱线展宽，可以计算核心黑洞的维里质量[8-10]。由于光由核心黑洞传播到宽线区有时间延迟，同时光致电离的特征时间较传播时延很短，因此宽线区的半径可以由这一时延与光速的乘积描述[11]。通过计算连续光变曲线和发射线光变曲线的互相关函数(Cross-Correlation Function, CCF)，可以确定平均时延长度与相关系数的关系，可以将使得相关系数值最大时的时延作为线谱与连续谱的时延，实际求解时一般通过求解互相关函数的质量中心(Centroid)确定平均时延长度[12]。反响映射的主要工作就是利用转移方程及观测量，确定平均时延长度。具体的求解过程利用了相关原理，通过相关函数可以确定发射线与连续谱的时延。

发射天体与反射天体之间的距离过近，同时都离地球极其遥远时，将不能区分发射信号与反射信号，此时接收信号是发射信号和反射信号的叠加。当反射体与发射源相对静止时，发射信号与反射信号之间的延迟固定不变，可以直接求解接收信号的自相关，且会出现两个相关峰值，峰值的间隔即给出了延迟大小。而当反射体与发射源之间有相对运动时，反射信号和发射信号的延迟将成为一个随时间变化的函数，此时对接收的信号求解自相关将得不到第2个相关峰，即不能直接给出延迟信息。本文提出了一种基于对接收信号在时域做变换的方法进行求解，可以有效地在有相对运动时求解延迟信息，具体的做法在基本原理部分进行说明。

双星系统是由两个围绕共同质心运动的恒星组成的恒星系统，较亮的一颗恒星被称作主星，另一颗被称作伴星。当双星系统中包含了致密天体，如白矮星、中子星或黑洞时，来自另一颗恒星(donor)的气体会在致密天体周围吸积(accretion)，产生大量的辐射。致密天体是白矮星时，被称作激变变星(cataclysmic variable)[13]。致密天体是中子星或者黑洞时，即是X射线双星。X射线双星会有更高的亮度，本文提出的方法可以在X射线双星系统得到更好的应用。

本文包含3部分内容，第1部分介绍了利用相关原理提取延迟信息的方法与缺陷，并提出了一种可以在发射天体与反射介质间有相对运动时提取延迟信息的方法，在此基础上给出了对双星系统轨道的估算方法；第2部分利用该方法，进行了MATLAB的模拟，验证了这种方法的可行性；第3部分是对该方法以及模拟结果的总结。

1 基本原理

利用相关原理可以提取时延信息，对于发射源与反射介质没有相对运动的情形，可以直接利用接收信号的自相关函数提取反射信号的时间延迟，从而给出反射介质的位置信息。当发射源与反射介质之间存在相对运动时，反射信号的时间延迟是时间的函数，此时已经不能直接用相关原理处理。双星系统沿椭圆轨道运动，因此不能直接使用自相关函数计算时延。利用参数空间搜索的方法，实现信号在时域的变换，可以计算反射信号与发射信号的时延，进行双星系统轨道的估算。

1.1 相关原理

这里研究的发射信号为有限带宽随机信号，其自相关信号是有一定展宽的脉冲函数。反射体与发射源相对静止，即信号传到接收者的时间差为常数。还需要做如下几点具体的说明。

首先，该发射信号具有一定的相干长度。由于处理信号的主要手段是进行相关运算，得到较好的相关结果的基本要求即是待处理信号具有一定的相干长度。因此只进行对具有良好的相干长度的信号进行处理。

其次，发射信号要足够强。由于被观测的双星系统距离地球很远，导致信号衰减幅度很大，同时信号反射时会大幅衰减，若发射信号不够强，可能导致接收的信号中反射信号成分过于微弱，无法提取所需的信息。

同时，由于被观测的双星系统与地球相距甚远，且伴星和主星间的距离较小，故可以认为接收的发射信号和反射信号是平行光。

记接收的信号为R(t)，发射信号为S(t)，在双星系统中，反射介质是伴星，记伴星的反射系数为κ，反射信号与发射信号的时间延迟为d，

反射信号可以表示为SRef(t)=κS(t-d)，

(1)

接收信号可以表示为R(t)=S(t)+κS(t-d)，

(2)

(3)

其中CS(τ)是有一定展宽的脉冲函数，如图1，除τ=0处有明显峰值外，其余的都是随机涨落。

接收信号R(t)的自相关信号为

(4)

利用(3)式，化简(4)式，可得

CR(τ)=(1+κ2)CS(τ)+κCS(τ+d)+κCS(τ-d).

(5)

可以看出，在τ=0处会出现峰值外，在τ=±d处也会出现峰值，由于反射信号抵达的时间一定比发射信号晚，τ=-d处的峰值没有物理含义，即说明如果有反射信号，且其延时为d时，对应的接收信号的自相关函数将在τ=d处出现峰值。这样，检验接收信号的自相关函数，即可以搜索出反射信号，确定在接收信号中是否存在反射信号。

1.2 存在相对运动情形

存在相对运动时，反射信号的时间延迟是时间的函数，记作d(t)，则反射信号为

SRef(t)=κS[t-d(t)],

(6)

图1 发射信号自相关函数。发射信号是模拟产生的有限带宽伪随机信号，信号长度为10s，相干长度为200ms，采样间隔为1ms

Fig.1TheAuto-CorrelationFunction(ACF)ofasequenceoftransmittedsignals.Here,thetransmittedsignalsaresimulatedpseudorandomsignalsofalimitedbandwidth.Thesignalsequencehasatotallengthof10s,acoherencelengthof200ms,andasamplingintervalof1ms

接收信号为R(t)=S(t)+κS[t-d(t)],

(7)

接收信号的自相关函数为

t.

(8)

可以看出，直接对接收信号进行自相关处理已经得不到明显的相关峰值。如图3，自相关函数仅在τ=0处出现了明显峰值。

记y=f(t)=t-d(t)，接收信号可改写为R(t)=S(t)+κS[f(t)]，其中d(t)由双星的轨道及运动信息确定，可以给出待定参数的具体表达式，这些参数是不随时间变化的，可以完全描述双星的轨道和运动。

图2 接收信号自相关函数。发射信号是模拟的有限带宽伪随机信号，信号长度为4 000 s，相干长度为100 ms，采样间隔为10 ms，反射信号时间延迟为1 500 s，反射系数为0.5，由于τ<0没有物理含义，只画出τ>0的部分
Fig.2 The Auto-Correlation Function (ACF) of a sequence of received signals. Here, the received signals are from transmitted signals simulated to be pseudo random signals of a limited bandwidth. The transmitted-signal sequence has a total length of 4000s, a coherence length of 100ms, and a sampling interval of 10ms. The time delay of the reflected signals is 1500s, and the reflection coefficient is 0.5. We only show the ACF forτ>0 becauseτ<0 has no physical meaning

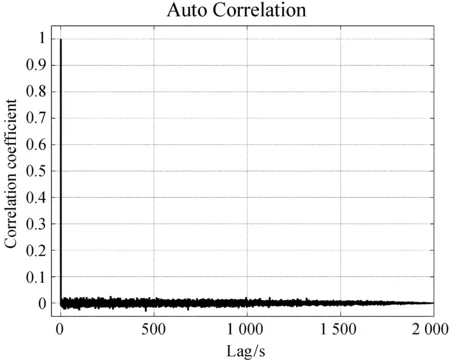
图3 接收信号自相关函数。发射信号是模拟的有限带宽伪随机信号，长度为2 000 s，相干长度为100 ms，采样间隔为50 ms，反射体作初始距离为600 ls，速度为0.06 c的匀速直线运动，反射系数为0.5，由于τ<0没有物理含义，只画出τ>0的部分
Fig.3 The Auto-Correlation Function (ACF) of a sequence of received signals. Here, the received signals are from transmitted signals simulated to be pseudo random signals of a limited bandwidth. The transmitted-signal sequence has a total length of 2000s, a coherence length of 100ms, and a sampling interval of 50ms. A reflector is assumed here to be moving in a constant velocity of a speed 0.06c. The initial distance of the reflector from the signal emitter is 600ls. The reflector has a reflection coefficient 0.5. We only show the ACF forτ>0 becauseτ<0 has no physical meaning

在对R(t)的时域做了如上映射后，可以得到新的信号：

RC(t)=S[D(t)]+S(t+t0)，

(9)

D(t)是t的函数，这里不关心D(t)的具体表达式。

接收信号R(t)与映射后信号RC(t)的互相关函数为

(10)

利用(3)式，化简可得

(11)

上式中积分项可以看作无穷小量，即互相关函数可以简化为

CRRC(τ)=κCS(τ-t0).

(12)

可以看出，互相关函数会在τ=t0处出现峰值，使用本文的修正方法，t0=0，因此在τ=0处出现峰值。

做上述时域映射需要给出f(t)=t-d(t)的除时间t外不含其它变量的表达式。在双星系统中，d(t)由轨道参数与运动参数唯一确定，但这些参数的具体值需要求解。可以给出这些参数的大致取值范围，遍历此范围内的值，每一个值对应的f(t)进行时域映射操作后计算接收信号R(t)与映射后信号RC(t)的互相关，当互相关有明显的峰值，并且峰值达到最大，即相关性最好时，可以认为此组参数是所要求解的轨道参数与运动参数。

因此进行参数空间搜索，对每一个参数组做时域映射并计算接收信号与映射后信号的互相关，找出互相关峰值最大时对应的轨道参数和运动参数，即是需要估算的双星系统的轨道参数与运动参数。

2 双星系统轨道估算的数值模拟

利用时域映射的方法，用模拟产生的信号进行数值模拟，搜索模拟接收数据中的反射信号，验证该方法。

模拟时采用的发射信号为有限带宽伪随机信号，在生成接收信号时，由于t时刻的反射信号是由该时刻之前对应的发射信号给出的，因此需要截取生成的发射信号中间的一段信号进行模拟。

针对X射线双星系统进行模拟，考虑反射体与发射天体、接收者在同一平面内的二维情形，且伴星围绕主星以椭圆轨道运行，该椭圆轨道的长轴和发射天体与观测者的连线垂直。建立以主星所在的椭圆焦点为极点的极坐标系，极径记作r，极角记作θ。这种情形可以看做是一个Edge On的双星系统。

图4 时域映射示意图。将y=f(t)分割成若干可以看作线性的小段，将(ti,yi)点与(ti+1,yi+1)点之间的线段局部放大画在图中。写出其两点式，即可以利用给出的映射方式得到映射后的直线yC=t

Fig.4 Illustration of the map of time to time delay. The map divides time into small intervals in each of which the map functiony=f(t) is approximately linear. The map within an arbitrary time interval is shown in the plot after being magnified, with the end points of the interval and corresponding map values marked as (ti,yi) and (ti+1,yi+1). The lineyC=tcan be determined using the linear-approximation formula of the mapping method

描述一个三维空间双星系统的轨道参数(Orbital Elements)有：倾角(Orbital inclination)、升交点黄经(Ecliptic longitude of the ascending node)、近星点经度(Ecliptic longitude of the periastron)、半长轴(Semimajor axis)、离心率(Eccentricity)、近星点时刻(Time at the periastron)[14]。在本文中，考虑二维平面内的情形，可以使用更少的轨道参数描述双星运动。

模拟伴星围绕主星做椭圆轨道运动的情形，选择利用离心率、半长轴、起始观测时的极角作为描述伴星轨道形状的轨道参数，伴星单位时间内扫过的面积是常数，可以用这一个参数作为描述伴星的运动的参数。所选择的4个参数可以完全描述伴星的轨道和运动。

生成长度为40 000 s的序列作为发射信号，由于存在时延，计算t时刻反射信号时需要之前的发射信号，因此计算接收信号时，只将后20 000 s的序列作为被接收的发射信号，同时被接收的反射信号可以利用整个40 000 s的序列通过计算时延给出。

利用搜索的结果，下面给出相关函数峰值随各个参数变化的曲线。

将其他参数固定在搜索求解出的数值，在给出的搜索范围改变θ0的值，给出相关函数峰值随参数θ0变化的曲线，在θ0=0处出现了明显的峰值。θ0表示观测初始时伴星的位置，图5说明，通过搜索，很好地确定了伴星初始位置。

图5 相关峰值随θ0的变化。将相关峰值归一化， 使得相关峰值的最大值为1

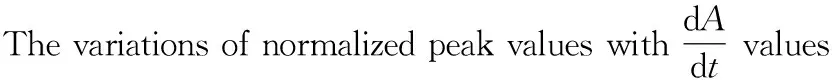
将其他参数固定在搜索求解出的数值，同时在给出的搜索范围改变参数e、a，画出相关函数峰值随参数e、a变化，在e=0.01、a=600 ls处出现了明显的峰值。参数e、a可以确定伴星的椭圆轨道形状，图7说明，通过搜索，很好地确定了伴星轨道。

3 结 论

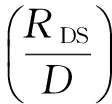
图7 相关峰值随e、a的变化。将相关峰值归一化， 使得相关峰值的最大值为1

Fig.7 The variations of normalized peak values witheandavalues

[1] 田文武, 杨雪娟. 当前超新星遗迹研究中的若干热点问题[J]. 天文学进展, 2010, 28(2): 97-111. Tian Wenwu, Yang Xuejuan. Light echoes and remnants of historically galactic supernovae[J]. Progress in Astronomy, 2010, 28(2): 97-111.

[2] Rest A, Suntzeff N B, Olsen K, et al. Light echoes from ancient supernovae in the Large Magellanic Cloud[J]. Nature, 2005, 438(7071): 1132-1134.

[3] Krause O, Birkmann S M, Usuda T, et al. The Cassiopeia A supernova was of type IIb[J]. Science, 2008, 320(5880): 1195-1197.

[4] Krause O, Tanaka M, Usuda T, et al. Tycho Brahe’s 1572 supernova as a standard Type Ia as revealed by its light-echo spectrum[J]. Nature, 2008, 456(7222): 617-619.

[5] Gouiffes C, Rosa M, Melnick J, et al. Light echoes from SN 1987 A[J]. Astronomy and Astrophysics, 1988, 198(1-2): L9-L12.

[6] 葛新成, 罗大成, 曹勇. 相关函数在数字信号处理中的应用[J]. 电光与控制, 2006, 13(6): 78-80. Ge Xincheng, Luo Dacheng, Cao Yong, Application of correlation function in digital signal processing[J]. Electronics Optics & Control, 2006, 13(6): 78-80.

[7] Peterson B M. Reverberation mapping of active galactic nuclei[J]. Publications of the Astronomical Society of the Pacific, 1993, 105(685): 247-268.

[8] Netzer H, Peterson B M. Reverberation mapping and the physics of active galactic nuclei[M]// Maoz D, Sternberg A, Leibowitz E M. Astronomical Time Series: Astrophysics and Space Science Library. 1997: 85-108.

[9] Peterson B M, Ferrarese L, Gilbert K M, et al. Central masses and broad-line region sizes of active galactic nuclei. II. A homogeneous analysis of a large reverberation-mapping database[J]. The Astrophysical Journal, 2004, 613(2): 682-699.

[10]Peterson B M. The central black hole and relationships with the host galaxy[J]. New Astronomy Reviews, 2008, 52(6): 240-252.

[11]Peterson B M, Horne K. Reverberation mapping of active galactic nuclei[C]// Planets to Cosmology: Essential Science in the Final Years of the Hubble Space Telescope. 2006: 89-98.

[12]Peterson B M. Variability of active galactic nuclei[C]// Advanced Lectures on the Starburst-AGN Connection, Proceedings of a conference held in Tonantzintla. 2001: 3-67.

[13]Smith R C. Cataclysmic variables[J]. Contemporary Physics, 2006, 47(6): 363-386.

[14]Benacquista M. An introduction to the evolution of single and binary stars[M]. New York: Springer, 2012: 13-28.

[15]Greiner J. The binary components of GRS 1915+ 105[C]// X-ray Binaries to Gamma-Ray Bursts: Jan van Paradijs Memorial Symposium. 2003: 111-120.

CN 53-1189/P ISSN 1672-7673

A Method of Estimating the Orbit of a Binary-Star System from Extracted Reflected Signals

Gao Yang1,2, Zhou Jianfeng1,2

(1. Center for Astrophysics, Department of Engineering Physics, Tsinghua University, Beijing 100084, China, Email: gaoyang12@mails.tsinghua.edu.cn; 2. Key Laboratory of Particle and Radiation Imaging (Tsinghua University) Ministry of Education, Beijing 100084, China)

Received signals from a binary-star system include signals reflected by the companion star. The time delay of reflected signals is related to the position and velocity of the companion star, so that the reflected signals after being extracted can be used to estimate the orbit of the binary-star system. In principle reflected signals can be extracted from the Auto-Correlation Function (ACF) of a received-signal sequence. However, a straightforward extraction is out of reach because of the relative motion within a binary-star system. In this paper we propose a method based on mapping the received signals in the time domain to those in a time-delay domain. Reflected signals can be extracted by calculating cross-correlation functions between raw received signals and signals in the time-delay domain after the mapping. We search for the peak value of cross-correlation coefficients within the space of parameters describing the binary-system orbit. The peak value is related to the values of the orbital elements. This allows finding the orbital-parameter values of a binary-star system. We have successfully tested the method through MATLAB simulations. Our simulations are for an X-ray binary system with an edge-on orbital plane, X-ray binary systems are usually rather luminous, which makes our method more easily applicable. There are 4 parameters needed to describe the elliptical-orbit motion of an X-ray binary system. These are the semi-axis, the eccentricity, the area swept per unit time by the line section from the centroid to the companion, and the initial polar angle of the companion. We finally discuss the influence of the reflection coefficient on the effectiveness of the method. We expect that our method is more effective for X-ray binary systems whose accretion processes are via Roche-lobe overflows than for other cases. This is based on some simple estimates and a case study of the X-ray binary system GRS1915+105.

Binary star; Time-delay estimation; Correlation function; Parameter space

国家自然科学基金 (11173038, 11373025)；清华大学自主科研计划 (20111081102) 资助.

2014-04-03；修定日期：2014-04-26

高 扬，男，硕士. 研究方向：天体物理. Email: gaoyang12@mails.tsinghua.edu.cn

P1

A

1672-7673(2015)01-0001-08