基于考虑结构体系刚度影响的高墩计算长度精细化分析

翁雅谷，高 宝，马越峰，戴显荣，史方华

(1．温州交投集团，浙江 温州 325003；2．浙江省交通规划设计研究院， 杭州 310006)

基于考虑结构体系刚度影响的高墩计算长度精细化分析

翁雅谷1，高 宝2，马越峰2，戴显荣2，史方华2

(1．温州交投集团，浙江 温州 325003；2．浙江省交通规划设计研究院， 杭州 310006)

在建立同时考虑墩顶支座和结构体系约束的等效刚度公式基础上，求解墩顶在弹性约束下的压杆计算长度系数精确方法。进而分别研究墩高和柱径对计算长度系数的影响，并基于不同的压杆计算长度系数选取方法，对高墩截面配筋的需求进行敏感性分析比较。

剪切变形；结构体系；弹性约束；计算长度

0 引 言

在山区公路项目中，受跨沟溪地形限制，采用较多的预制装配式高墩桥梁。对于采用先简支后连续结构体系的T梁或组合箱梁桥，其合理跨径选择以及下部结构设计均受墩高要素控制，而桥墩的尺寸选型及其强度、抗裂设计均与桥墩计算长度的选取密切相关，尤其对于高墩，合理确定计算长度显得尤为重要[1-2]。但目前规范[3]对压杆构件计算长度系数的选择，定义较为模糊，如仅指定若干理想状态，如上下两端固结时，则压杆长度系数为0.5；下端固结、上端自由时，则压杆长度系数取2.0等。对于预制装配式高墩桥墩，上述理想边界状态与实际情况均有较大的出入，如直接采用理想状态下的压杆长度系数，会使计算结果或偏保守、或偏不安全[4-6]。

对于长细比较大的高墩，墩身相对较柔，通常墩顶水平抗推刚度与墩顶支座剪切刚度大致在可比较的量级上，因此墩顶支座形成的弹性约束影响不容忽略，这里可定义为“柔墩强约束”边界状态；但对于较矮的桥墩，通常墩顶水平抗推刚度远大于墩顶支座的剪切刚度，墩顶支座形成的弹性约束影响相对较小，为“强墩弱约束”边界状态。另外如不计上部主梁的轴向伸缩变形，即假定主梁为刚体，则同一联其他桥墩可共同组成整体框架体系，其对分析对象的桥墩也构成一种约束影响。因此，如精细化确定的计算桥墩的压杆计算长度，需同时考虑上述两种约束影响，即墩顶支座和整联框架体系内其它桥墩形成的弹性约束，两者组成一个串联刚度体系。这里需指出，假如仅计墩顶支座约束，而忽略后者影响，则相当于假定支座顶为固结状态，会高估墩顶的约束刚度，进而会使压杆长度系数的计算产生较大的误差。

1 考虑墩顶弹性约束的压杆长度系数计算

1.1 墩顶约束刚度等效计算

对于先简支后连续结构体系的T梁或组合箱梁桥，如单联跨数不超过5跨，通常中间连续墩均采用普通板式橡胶支座，假定普通板式橡胶支座和梁体、墩顶接触良好，弹性板与混凝土之间磨阻系数一般可达到0.3，此时板式支座与墩梁混凝土接触面之间不会发生相对滑移，但在温度变化、制动力等外部荷载作用下，支座会产生可恢复的弹性剪切位移。另外不考虑上部主梁轴向伸缩变形的情况下，与桥墩相比，主梁可视为刚体，其抗弯刚度远大于桥墩抗推刚度[7-9]。如基岩埋藏较浅的山区桥梁，桥墩受力的边界条件，可视作下部为固结(或者按“m法”考虑桩入土一定深度处嵌固，此处不再展开)，墩顶承受一定的弹性约束，因此确定桥墩压杆计算长度的关键，就在于精确确定墩顶弹性约束。

图1 整体框架体系桥墩墩顶约束刚度计算示意

对于一联结构体系内中间第i个桥墩，其对应支座顶位置的水平组合刚度k组合i有两部分组成，分别为该桥墩自身的抗推刚度k墩i和支座的抗剪切刚度k支i，两者为并联体系。

k组合i=k墩i·k支i/(k墩i+k支i)

(1)

其中，k墩i=3mEIh/H3，k支i=nA/t，式中，EIh为桥墩抗弯刚度，H为墩高，m为墩柱个数，n为先简支后连续体系转换后墩顶设置一排板式支座个数，A为一个支座的平面面积,G为橡胶支座的剪切弹性模量，t为支座的橡胶层厚度。如为变截面高墩，则k墩i可根据截面、墩高换算成等效抗推刚度。

(2)

式中，j为同一联内其它桥墩的编号,j≠i。

单独以第i个桥墩为分析对象，其首先受到第i个桥墩的墩顶橡胶支座的剪切刚度约束，其次受到同一联结构体系内其它桥墩提供的刚度约束，两者组成并联体系，构成分析对象的墩顶等效约束刚度k等效i，计算如下：

(3)

1.2 考虑等效弹性刚度约束的桥墩计算长度数值解法

上述计算模型，可简化为下端固结，上端为弹性铰支撑的压杆，建立弯曲平衡方程如下：

Ely″+py=pδ-k等效δ(L-x)

(4)

(5)

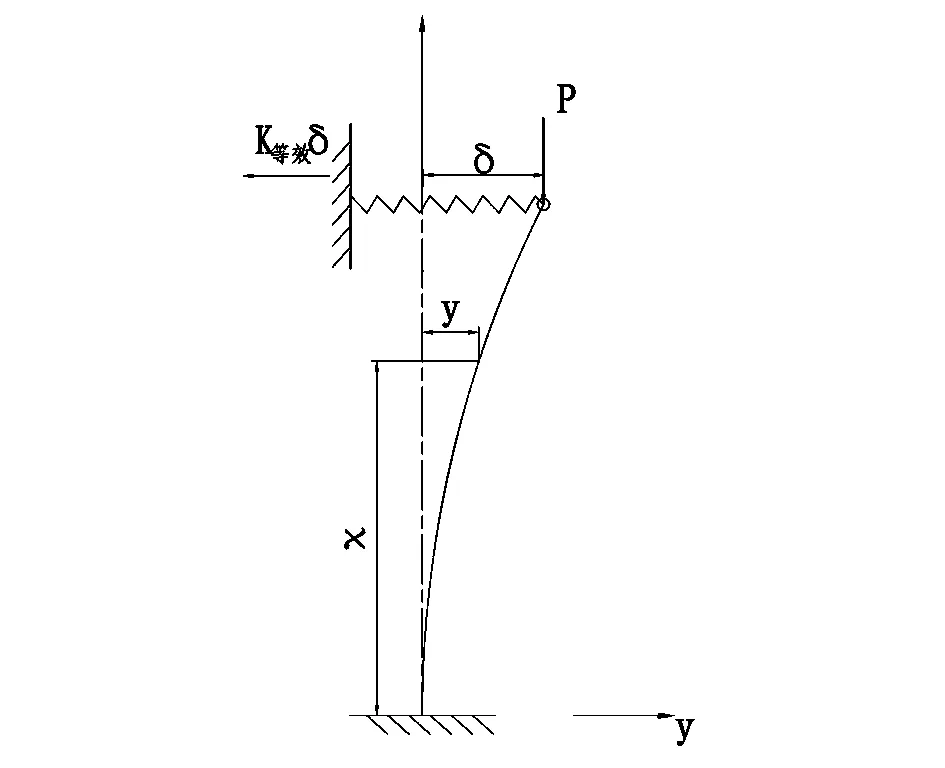
图2 上端弹性支撑压杆计算简图

由下端固结边界条件知， 当x=0时，y=0，y′=0得到

由上端弹性铰支撑边界条件知，当x=L时，y=δ，得到稳定方程如下：

(6)

上述方程可通过函数编程，采用数值法逐次逼近求解，得到最小的α，即可求得压杆长度系数μ：

(7)

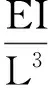
2 算例分析

某山区高速公路为受地形限制，桥隧结构占比较高，局部出现桥隧相连，跨沟溪最大墩高约50m，桥梁结构以采用40m跨径的先简支后连续T梁为主，桥宽24.0m,单幅5片梁板，梁高2.5m。下部桥墩均采用双柱式桩柱墩形式，桩柱直径根据墩高作相应调整。中间连续处桥墩墩顶设置一排板式橡胶支座，规格为GJZ450×550×104mm。桥位处覆盖层一般埋藏较浅，局部基岩裸露，桩基础以端承桩为主。墩柱均采用C30混凝土。

2.1 不同墩高的计算长度系数分析

选取常用的四跨一联40mT梁进行分析，根据不同的墩高范围，设计采用不同的桩柱直径，根据前述公式得到计算长度系数(见图3)。从图中可以看出，随着墩高增加，计算长度系数会逐渐减小。当墩身越矮时，计算长度系数越趋向于2.0，此时墩身本身抗推刚度较大，上端弹性约束较弱，越接近下端固结，上端自由的边界状态；当墩身越高时，计算长度系数越趋向于1.0，此时墩高本身抗推刚度较小，而上端弹性约束同比较大，计算长度系数接近于两端铰接的状态。由此可见，桥墩的计算长度系数本质上与墩身抗推刚度与墩顶约束刚度比相关，取值范围介于1.0～2.0，低墩时接近上限，高墩接近下限。

图3 40mT梁不同墩高的计算长度系数比较

2.2 墩柱直径的影响分析

设定在35m墩高情况下，假定不同的墩柱直径，考察计算长度系数的变化规律。从图4情况看，随着墩柱直径增加，计算长度系数逐渐增大，如柱径选用2.2m,则对应计算长度系数为1.266；如选用2.5m，则对应计算长度系数为1.369。分析原因，随着墩柱直径增加，则墩身刚度会逐渐增加，相应的墩顶约束刚度效应减弱，则计算长度系数会逐渐增大。由于较大的计算长度系数对墩身受力计算并不利，因此结构设计时，尺寸选型在满足基本荷载要求的情况下，不应保守选用较大的尺寸，否则结构会增加不必要的配筋。

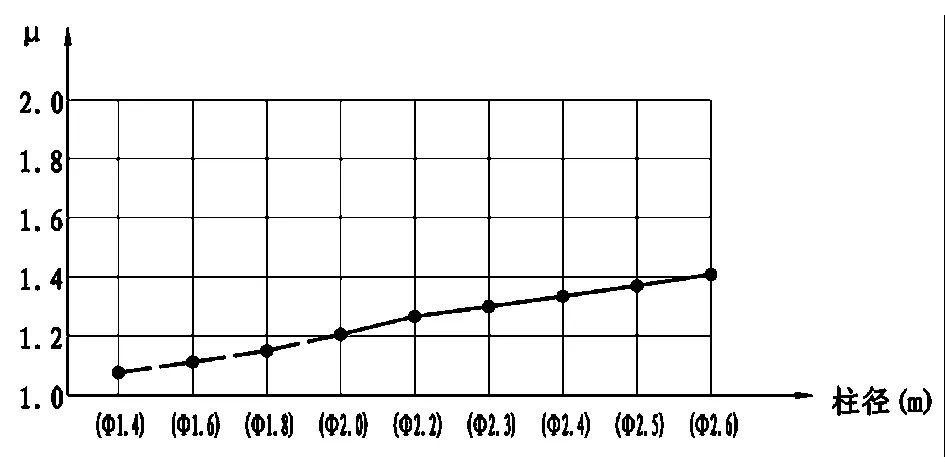
图4 相同墩高(假定35m)

2.3 不同计算长度系数对高墩配筋的敏感性分析

同样设定在35m墩高情况下，柱径确定为2.2m,如计算长度系数选择不同，则影响偏心受压构件的偏心距增大系数，进而影响墩柱截面的配筋。一般情况下，桥墩承受的水平力通常为温度荷载、制定力等组合，竖向力为恒载与活载等组合，墩底作为偏心受压构件，其配筋受承载能力极限组合控制。图5为4选择四种边界模式，比较不同的计算长度系数对高墩配筋的影响分析。第一种为按本文公式推导计算长度，对应截面配筋需求为364mm2；第二种假如不考虑结构体系的刚度约束，仅计入支座约束，支座顶与主梁接触点视作不动铰约束，则推算计算长度系数为0.878，对应截面配筋需求为154mm2，配筋量仅为前者的42%；假如按下端固结、上端自由状态计算，截面配筋需求为815 mm2，则配筋量需求为第一种的2.24倍；假如按两端铰接状态计算，截面配筋需求201mm2，则配筋量需求为第一种的55%。

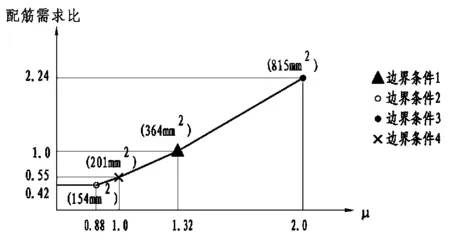
图5 不同计算长度系数下高墩配筋比较

由以上分析，高墩承载能力配筋需求对计算长度系数的选取非常敏感，因此只有精确的确定计算长度系数，才能确保桥墩结构设计的经济、合理、安全。

3 结 语

1)确定高墩计算系数需同时考虑墩顶支座约束和同一联结构体系内其它桥墩的刚度约束贡献，利用本文推导的墩顶等效约束刚度计算公式，可精确确定高墩的计算长度系数，从力学本质上看，桥墩的计算长度系数受制于墩身抗推刚度与墩顶约束刚度比。

2) 随着墩高增加，桥墩的计算长度系数逐渐减小，取值范围介于1.0～2.0。当墩身越矮时，计算长度系数趋向于下端固结、上端自由的状态；当墩身越高时，计算长度系数趋向于两端铰接的状态。

3) 随着墩柱直径的增加，计算长度系数逐渐增大，结构尺寸选型在满足基本荷载要求情况下，不应过于保守选用较大的尺寸，否则结构配筋会更不经济。

4)高墩结构配筋需求对计算长度系数非常敏感，如墩顶不考虑结构体系刚度约束，仅计入支座约束影响，会明显低估计算长度系数，造成配筋偏少的不安全设计。只有精确确定长度系数，才能确保桥墩结构设计的经济、合理、安全。

[1]陈立平，等．山区高速公路桥梁高桥墩压杆稳定性设计分析[J]．公路交通科技，2006(12)：107-109.

[2]程祥云．高桥墩设计计算的两个问题[J]．重庆交通学院学报，2000(2)：6-10.

[3]JTG D62-2004，公路钢筋混凝土及预应力混凝土桥涵设计规范[S]．

[4]李军，等．梁桥高墩计算长度的一种计算方法[J]．城市道桥与防护，2009(6)：50-52．

[5]齐宏学，等．装配式梁桥高墩计算长度系数探讨[J]．中外公路，2011(11)：51-55.

[6]曾照亮，等．高墩计算长度探讨[J]．中外公路，2008(5)：160-162.

[7]项海帆．高等桥梁结构理论[M]．北京：人民交通出版社，2001．

[8]李存权．结构稳定和稳定内力[M]．北京：人民交通出版社，2000．

[9]刘光栋．杆系结构稳定[M]．北京：人民交通出版社，1988．

Accurate Analysis of the Calculated Length Coefficient of High Pier by Considering Structure System Stiffness

WENG Yagu1, GAO Bao2, MA Yue-feng2, DAI Xian-rong2, SHI Fang-hua2

(1．Wenzhou Communications Investment Group， Wenzhou 325003，china；2．Zhejiang Provincial Institute of Communications Planning Design ﹠Research, Hangzhou 310006,China)

Considering the pier top bearing and the constraint of the structural system, the equivalent stiffness formula has been established, and the accurate calculated length coefficient method of pressure bar in the pier top under elastic restraint is also derived. then the Influence of pier height and column diameter is respectively discussed. Based on the different calculation length coefficient of pressure bar, the sensitivity of the high pier reinforcement demand is analyzed .

shear deformation；structural system ；elastic restraint；calculated length coefficient

2015-06-02

翁雅谷(1973-)，男，浙江温州人，高级工程师，E-mail:903307050@qq.com。

U443.22 ?

A ?

0.3969/j.issn.1671-234X.2015.03.004

1671-234X(2015)03-0017-05