指数平滑法在青少年吸毒分析中的应用

王松敏，刘丽芳，吴翠芳

(武警学院，河北 廊坊 065000)

指数平滑法在青少年吸毒分析中的应用

王松敏，刘丽芳，吴翠芳

(武警学院，河北 廊坊 065000)

采用定量分析的方式，运用指数平滑法对2004至2013年某地区青少年吸毒的相关数据进行了相关分析和预测，为相关部门采取措施提供了更科学的依据。

青少年吸毒；指数平滑法；分析预测

要成功预防和减少青少年吸毒违法行为的发生，就必须了解青少年吸毒的现状及特点，为制定和完善青少年吸毒的措施提供依据。[1]为了使相关决策更加科学，文章借助了一种数学方法——指数平滑法对某地区青少年的吸毒问题进行相关分析和预测，进而避免了只从定性的角度分析青少年吸毒这一问题。

一、吸毒数据的选取及简单分析

本文选取了2004-2013年某地区21岁以下(不含21岁)青少年吸毒的相关数据(来源于官方网站http：//www.nd.gov.hk/)。数据中的“所有呈报人数”包含“首次被呈报人士”和“曾被呈报人士”。下面的表1给出了2004-2013年“所有呈报人数”与“曾被呈报人士”随年份变化的数据，以及该地区吸毒青少年“曾有犯罪记录”的人数。

把上面的数据用散点图画出后，可清楚地看出其变化趋势(见图1)：三组数据在2008年或2009年达到高峰后持续下降。这说明现行政策还是比较有效的。

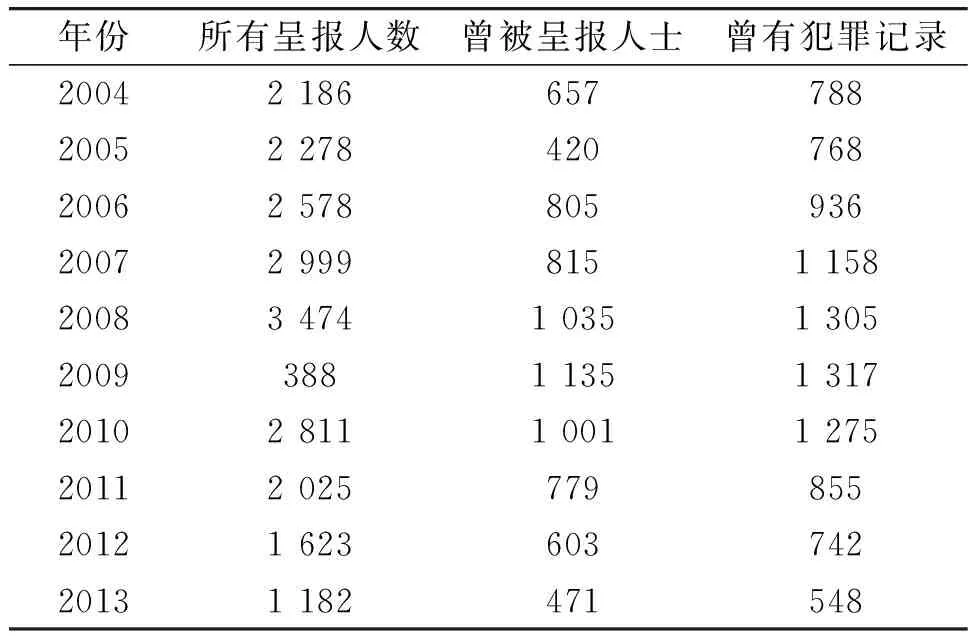
表1 2004-2013年某地区青少年吸毒的相关数据

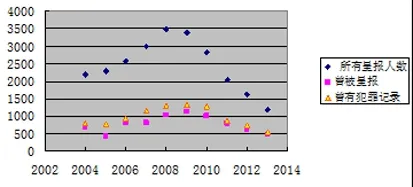
图1 2004-2013年某地区青少年吸毒数据散点图

但是，“曾被呈报人士”及吸毒青少年中有“曾有犯罪记录”的人数占青少年吸毒总数的比例(见表2)整体上都处于上升的趋势，这点通过下面的图2可清楚地看出。

图2 两组数据占总数的百分比的散点图

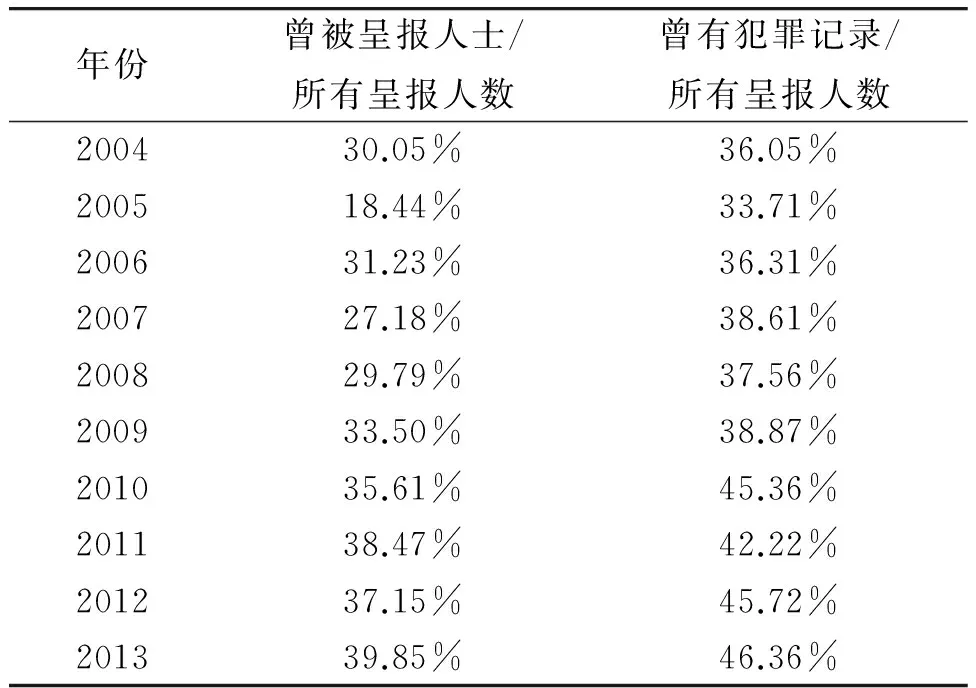
年份曾被呈报人士/所有呈报人数曾有犯罪记录/所有呈报人数200430.05%36.05%200518.44%33.71%200631.23%36.31%200727.18%38.61%200829.79%37.56%200933.50%38.87%201035.61%45.36%201138.47%42.22%201237.15%45.72%201339.85%46.36%

因此，有必要弄清楚表2中的数据在未来几年内的发展趋势，进而为相关部门更好地制定禁毒措施提供重要的参考依据。下面先介绍指数平滑法，然后运用该方法对“曾被呈报人士”及吸毒青少年中有“曾有犯罪记录”的人数这两组数据进行分析及预测，并对青少年吸毒的预防工作提出合理化建议。

二、指数平滑法

指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，其原理是任一时间点的指数平滑值都是本时间点的实际观察值与前一时间点的指数平滑值的加权平均。这里的权重主要是平滑系数。平滑系数越小，实际观察值所占比重越小，平滑作用越强；反之，平滑系数越大，平滑作用越弱。一般情况，原数据较平稳，波动不大时，可选用较小的平滑系数(0.05～0.2)；反之，当数据波动较大，或变化趋势明显时，可选较大的平滑系数(0.3～0.8)[2]。

在情报分析中，当时间序列无明显线性趋势时，可考虑用一次指数平滑法；若时间序列大致呈线性趋势或者从某一项开始具有线性趋势，那么用一次指数平滑法就会出现滞后偏差，就需要对所得结果进行修正，此时可考虑用修正指数平滑法进行预测。

(一)一次指数平滑法

设时间序列为y1,y2,…,yt,…yn，则一次指数平滑预测模型为:

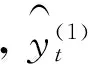
(二)修正指数平滑法

该方法也称为二次指数平滑法，即对一次指数平滑序列再进行一次指数平滑，具体公式如下：

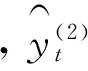
其中，t为当前时期，l为预测时期与当前时期的时间差，Yt+l为第t+l时期的预测值，at与bt为线性修正系数，计算公式为:

三、具体应用与分析

(一)指数平滑法在青少年吸毒分析中的应用

从图2可知，表2中的两组样本数据整体都呈线性趋势，且都有10%左右的波动差异。为提高预测精度，我们分别选取平滑系数α=0.2，α=0.3及α=0.4进行比较，进而选择平均绝对误差最小的α进行预测。

两组数据的初始值都取各自原始数据前三项的平均值，即“曾被呈报人士占总数比例”的一次指数平滑和二次指数平滑的初值都是

(0.300 5+0.184 4+0.312 3)/3=0.265 7

“曾有犯罪记录占总数比例”的一次指数平滑和二次指数平滑的初值都是

(0.360 5+0.337 1+0.363 1)/3=0.353 6

考虑到近期数据与未来的预测更贴切，故以t时期对应的平滑值为基础建立线性修正模型预测下一个t+1时期的值，即由公式(3)可得:

Yt+1=at+bt·1=at+bt

具体计算结果见下面的表3与表4。

表3 “曾被呈报人士占总数比例”在不同平滑系数下的预测值及对应的绝对误差

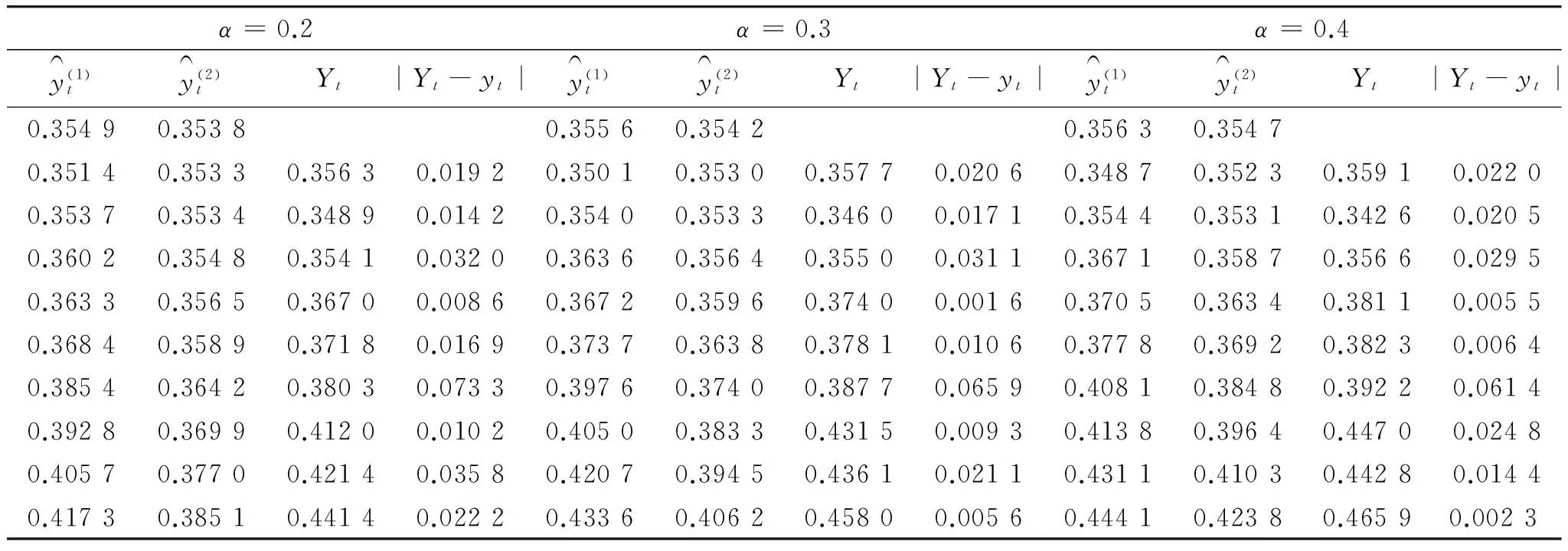
表4 “曾有犯罪记录占总数比例”在不同平滑系数下的预测值及对应的绝对误差

下面利用下式计算两组数据在不同平滑系数下的预测值对应的平均绝对误差:

另外，表4中，当α=0.2时，MAD=0.025 8；当α=0.3时，MAD=0.020 3；当α=0.4时，MAD=0.020 7。可以看出，也是α=0.3时对应的平均绝对误差最小，从而也选取平滑系数α=0.3做预测。

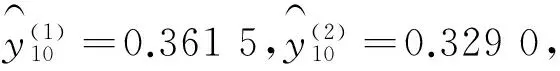
当l=1时，代入(5)式可得Y11=0.408 1；当l=2时，代入(5)式可得Y12=0.422 1。由此预测得2014年及2015年“曾被呈报人士占总数的百分比”分别为40.81%与42.2%。

另外，采用同样的步骤，对第二组数据按照上述方法处理，可得其线性修正模型为:

当l=1时，代入(6)式可得Y11=0.472 6；当l=2时，代入(5)式可得Y12=0.484 3。由此，根据此预测得，2014年及2015年“曾有犯罪记录占总数的百分比”分别为47.26%与48.43%。

(二)结果及对策分析

从上面的预测结果可知，青少年吸毒中“曾被呈报人士占总数的百分比”和“曾有犯罪记录占总数的百分比”都有增加趋势，复吸和犯罪是该地区青少年吸毒问题中十分突出的问题。

若按照现在的发展趋势，从上面的分析可得该地区21岁以下(不含21岁)吸毒的青少年中，复吸的人数每年将按照1.4%的百分比增长，有犯罪记录的人数每年将按照约1.17%的百分比增长，即这两组人群将逐渐成为该地区青少年吸毒的主力军。

另外，从表1或图1可以看出，复吸的人数总是小于有犯罪记录的人数，且当复吸人数增加(或减少)时，对应的有犯罪记录的人数也会增加(或减少)，可见复吸青少年与犯罪问题的关联性，即可推断复吸中部分青少年会走上犯罪的道路。

对于戒毒者来说,生理上的脱毒可以在短时间完成,但其心理康复和戒除“心瘾”则需要相当长时间。再加上青少年一般意志力较薄弱，在周围吸毒人群的诱惑下，往往更不堪忍受戒断症状的痛苦，而重新走上了复吸的道路，这也是复吸人员成为该地区吸毒青少年主要人群的原因。

吸毒是一种高额消费，青少年大多无固定经济来源，往往会采用非法的手段来获得钱财，以致诱发多种违法犯罪，从而给自身发展和社会带来极大的危害。另外，有犯罪记录的青少年回归社会后，有时由于缺乏社会帮扶和家庭原因，加之心理空虚自身没有重新融入社会的动力，往往会依赖毒品消磨时光，忘记烦恼，寻求精神上的慰藉。因此相关部门一定要重视青少年吸毒问题和犯罪问题的关联性。

预防青少年复吸和因吸毒而导致的犯罪是一项非常复杂而艰巨的工作,需要全社会的高度重视和全方位的共同努力。[4]根据前面的分析，相关部门应做好以下几方面的工作。

第一,社会各部门应密切配合。强制戒毒所、公安缉毒机构、学校单位、家庭、社区、管辖地公安派出所,在禁毒问题形成共识，主动协调配合,才会收到成效。第二，借助大众传媒传递正能量。现在大众传媒已存在于生活的方方面面,借助于他们对吸毒的相关知识进行宣传,对青少年进行教育指导,相信是一种影响广泛的好办法。[5]第三,改善或改变青少年戒毒者的原来生活环境。斩断与“道友”或“粉友”的联系，彻底使他们脱离原有的生活环境。

[1] 万志红.云南青少年吸毒现状分析[J].云南警官学院学报，2007,62(1):52-55.

[2] 邓超风.指数平滑模型探讨[J].中国水运：学术版，2006,(9).

[3] 张桂喜，马立平.预测与决策概论[M].北京：首都经济贸易大学出版社，2006.

[4] 缪清鑫.关于吸毒青少年戒毒问题的思考[J].天府新论,2004,116(2):82-84.

[5] 栾昕畅.香港青少年吸毒影响因素与解决对策[J].中国学校卫生，2010,31(6):767-768.

(责任编辑 杜 彬)

The Application of Exponential Smoothing Method in the Analysis of Youth Drug Abuse

WANG Songmin， LIU Lifang， WU Cuifang

(TheArmedPoliceAcademy，Langfang，HebeiProvince06500，China)

Having collected data related to youth drug abuse in an area from 2004 to 2013, the paper analyzes and predicts the data by exponential smoothing, aiming at providing scientific suggestion for drug control efforts.

youth drug abuse; Exponential Smoothing; analysize and predict

2015-06-16

河北省统计科学研究(计划)项目“基于灰色系统理论的吸毒数据统计与分析”(2014HZ03)

王松敏(1982— )，女，河南清丰人，副教授； 刘丽芳(1978— )，女，河北大城人，讲师； 吴翠芳(1980— )，女，山东莱芜人，讲师。

D669.5;O212.1

A

1008-2077(2015)09-0019-04