基于改进人工势场法的机器人路径规划的研究

潘 洲，万 衡，王凯凯，胡中华

PAN Zhou, WAN Heng, WANG Kai-kai, HU Zhong-hua

（上海应用技术学院 电气与电子工程学院，上海 201418）

0 引言

随着智能技术的不断发展，自主移动机器人路径规划技术的研究也成为了各国学者研究的热点。研究路径规划的意义是想让机器人拥有感知、规划和控制等高等技能，其基本思想是旨在按照某一评估准则（像移动耗费最小、路径最短、时间最少等），在存在障碍物的室内复杂场景下，搜寻一条从起点到目标点的无碰撞的路径[1]。目前常用的路径规划方法主要有人工势场法[2]、模糊逻辑算法[3]，可视图法[4]，栅格法[5]，蚁群算法[6]，神经网络法[7]等。由于人工势场法相对于其它算法来说具有反应快速、计算简单以及实时性强等优点，因而获得了广泛的应用。

虽然人工势场法有很多优点，但也存在固有的缺陷：局部极小问题。文献[8]提出了一种基于虚拟障碍点（Virtual Obstacle Point）的方法来处理局部极小问题。该方法在一定程度上解决了局部极小问题，但还存在一定的缺陷：第一，在某种特殊情况下会反复陷入局部极小点，无法到达目标点；第二，盲目的放置虚拟障碍点的位置，未考虑路径规划的效率问题。本文在此基础上，提出了一种改进的虚拟障碍点法（Improved Virtual Obstacle Point），改进后的算法可以很好的解决文献[8]中所存在的问题。仿真结果表明，APF-IVOP算法更具优越性。

1 传统人工势场法原理

人工势场法是由Khatib[9]提出的一种方法。其基本思想是设计出一种抽象的虚拟力场来处理机器人的运动，目标对机器人产生“引力”，障碍物对机器人产生“斥力”，再利用它们的合力来控制机器人的动作。在势场中包含有斥力极和引力极，障碍物区域属于斥力极，目标区域为引力极。引力极和斥力极周围产生相应的势场。移动机器人在虚拟势场中获得一定的抽象力，推动移动机器人避开障碍物，朝目标运动。

势场函数包含引力场函数和斥力场函数。在势场中，障碍物O（Obstacle）对机器人R（Robot）产生排斥力，且距离越近，排斥力就越大，反之就越小；目标点G（Goal）对机器人R产生引力，且距离越近，引力就越小，反之就越大。最后用引力与斥力的合力来牵引移动机器人运动，构造的势场函数表示为：

式中，U为总势场，UO为斥力场，Ug为引力场。势场中的合力为：

式中，F为合力，决定了移动机器人的运动；Fg为引力，FO为斥力。

在势场中移动机器人的受力分析图如图1所示。

2 APF-IVOP算法对局部极小问题的优化

所谓局部极小，就是在多障碍物环境中，当机器人、障碍物、目标点在同一条线上，并且障碍物在机器人和目标点之间，在机器人尚未到达目标点时，由于障碍物的位置因素，机器人在某一点受力平衡，机器人所受到的引力和斥力恰好大小相同方向相反，此时的合力为0，从而导致该点的势场全局最小，致使机器人在此处停止不前或者徘徊，不知道下一步的运动方向，造成机器人无法到达目标点，这就是人工势场法的局部极小值问题。为了让机器人逃出局部极小值，研究学者们提出了很多的方法[10,11]，比如虚拟目标点法、沿墙走、随机逃走法等。

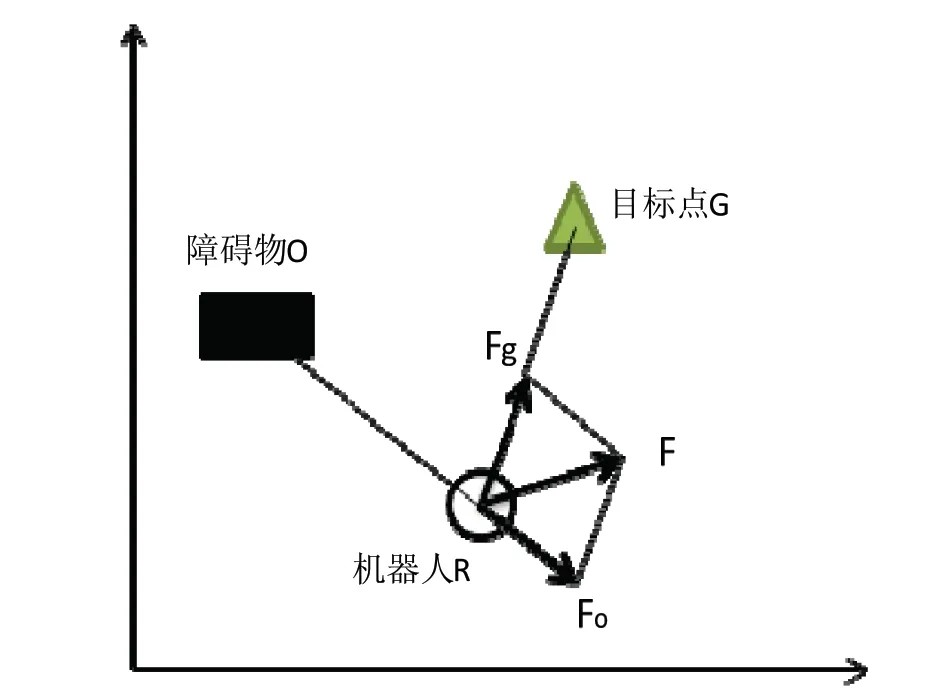
图1 机器人受力分析图

本文首先对文献[8]中所提到的算法进行叙述并分析其所存在的缺陷，然后再针对其存在的缺陷提出改进方法。

文献[8]中的方法如下：

1）如图2所示，首先连接局部极小点R和目标点G。

2）在RG上选择一点V，使RV=dv，该点就是虚拟障碍点的位置。

3）根据下式得到V点的坐标值，并记录到虚拟障碍点的信息表中。

式中，(xr,yr)、(xv,yv)、(xg,yg)分别是R、V、G的坐标值；atan2(yg-yr，xg-xr)为直线RV与X轴的夹角，加入的随机数，避免机器人、虚拟障碍点、目标点在同一条直线上时，消除一个局部极小点后又产生一个新的局部极小点，如此反复，使得机器人无法摆脱局部极小点。

4）在计算虚拟力时，虚拟障碍点的斥力计算和普通障碍物一样。

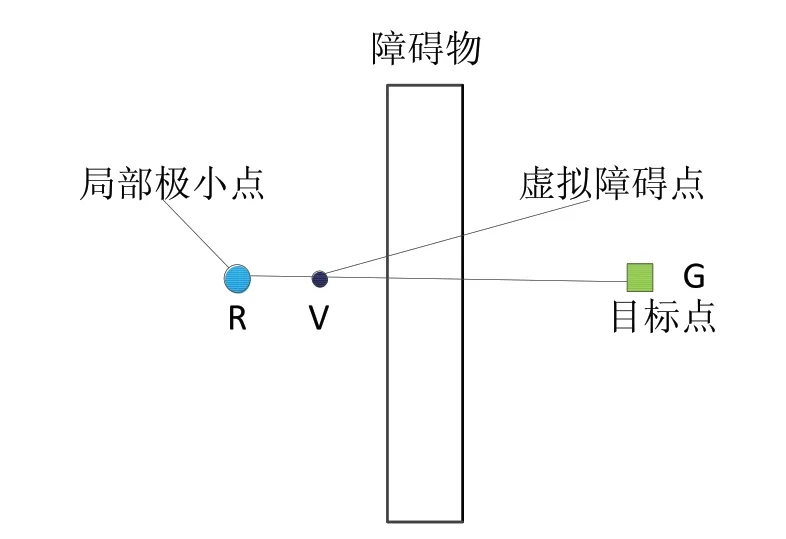
图2 文献[8]中虚拟障碍点位置选择

从本质上说，原文献中设置虚拟障碍点的方法就是随机在机器人附近添加一个虚拟障碍点，这样做是有缺陷的：

2）文献[8]并没有判断机器人所处位置与障碍物之间的关系，这样盲目的添加虚拟障碍点，很有可能使得机器人多走很多弯路，不仅增加了机器人的规划时间，降低了规划的效率，而且完成路径规划的代价也增多。

本文中的做法是：

1）如图3所示，首先连接局部极小点R和目标点G，取dv为一个适当的常数。

2）其次判断机器人、障碍物、目标点间的位置关系：首先通过传感器获取周围障碍物的信息，计算出障碍物两边与连线间的夹角判断的大小。

计算公式如下：

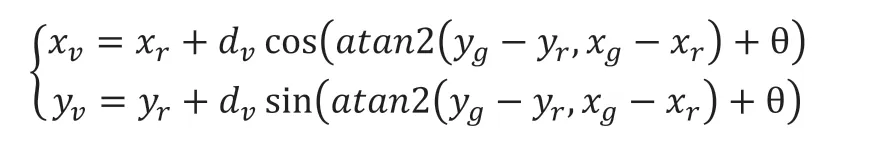
式中，(xr,yr)、(xv,yv)、(xg,yg)分别是R、V、G的坐标值；atan2(yg-yr,xg-xr)为直线RG与X轴的夹角，

6）在计算虚拟力时，虚拟障碍点的斥力计算和普通障碍物一样。

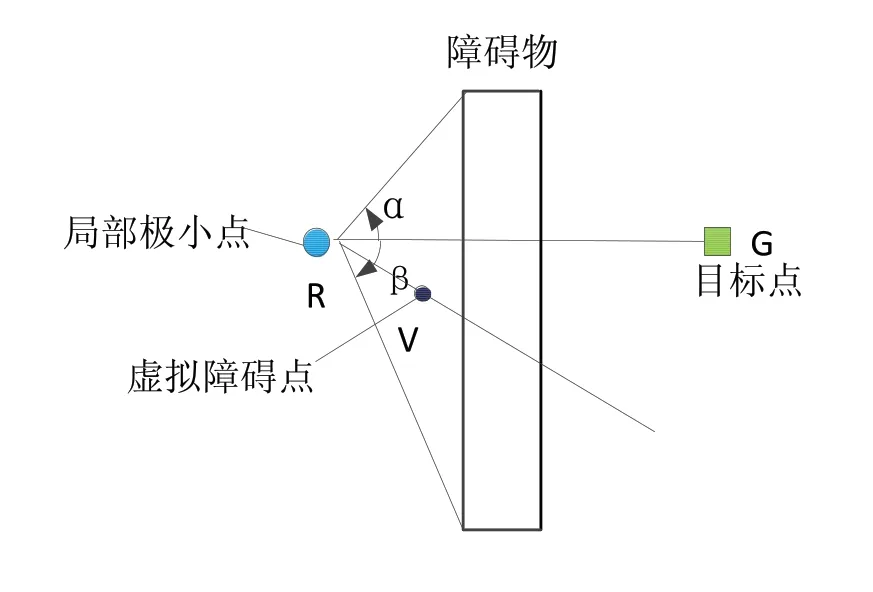
图3 本文虚拟障碍点位置选择

利用APF-IVOP算法进行路径规划的过程如下：

1）初始化起点和目标点。

2）判断机器人是否到达目标点，如果是，则成功找到路径，路径规划结束；如果否，则转3）。

3）判断机器人是否陷入局部极小，如果是，则添加一个虚拟障碍点后转4）；如果否，直接转4）。

4）根据势场模型，计算当前位置的合力。

5）计算机器人下一步位置，将机器人由当前位置移至下一位置，转2）。

APF-IVOP算法流程如图4所示。

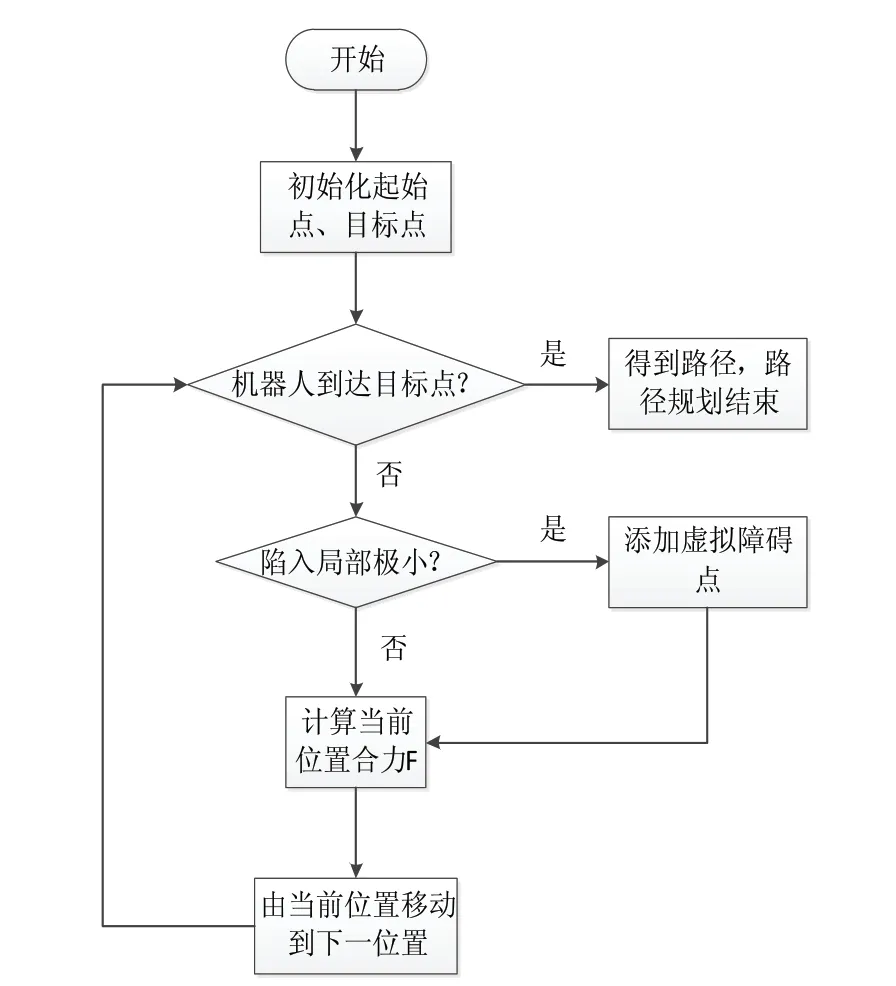
图4 算法流程图

3 仿真实验与结果

针对上文提到的部分问题进行了MATLAB仿真，仿真结果如图5、图6所示。从图5中可以看出，当RV与X轴夹角为0时，文献中的算法会使得机器人无限陷入局部极小点，无法到达目标点，本文中的算法有效的解决了这个问题。从图6中可以看出，在机器人陷入局部极小值时，当RV与X轴夹角不为0时，原文献中的算法在没有对环境进行判断的情况下随机选取了较差的路径，连续两次陷入局部极小点，耗费了大量的时间，完成路径规划所花费的代价较高，规划出的路径也较长，规划路径的效率偏低；经过判断后的路径，即用本文中算法规划的路径，其效果要明显好于未经过判断的路径，大大缩短了规划的时间，规划的效率明显提升，完成路径规划所消耗的代价明显降低，规划出的路径也更短更优。通过以上仿真可以看出，APF-IVOP算法具有一定的优越性和有效性。

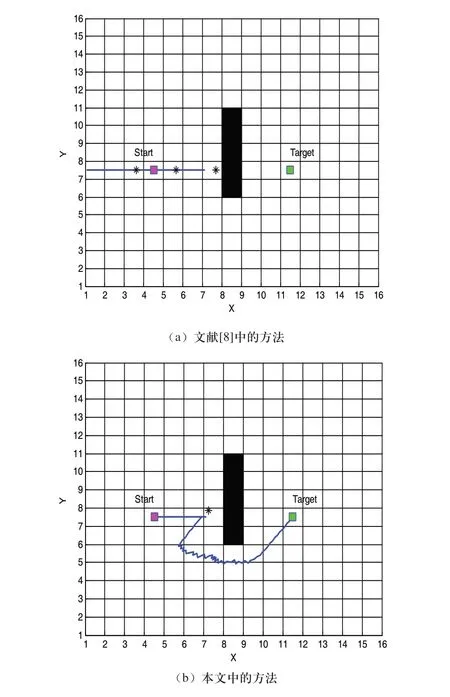
图5 RV与X轴夹角为0时

图6 RV与X轴夹角不为0时

4 结束语

人工势场法因其结构简单、容易实现、能够平滑路径等优点，而得到了广泛的重视。本文针对传统人工势场法存在的局部极小问题，提出了一种改进的人工势场法，即APF-IVOP算法。该算法可以对周围环境进行探测并能够动态设置虚拟障碍点的位置，同时能够有效处理不同位置关系下的局部极小问题，该算法具有简单且易于实现、计算速度快、实时性好等优点。基于APFIVOP算法下的路径规划，所规划出来的路径更优，消耗的代价更低，路径规划的效率也更高。最后通过MATLAB仿真验证了APF-IVOP算法的有效性。另外，对于路径的平滑度和震荡问题的改进可以采用文献[12]中提到的采用模糊逻辑算法来进行改进。

[1] 李磊,叶涛,谭民,等.移动机器人技术研究现状与未来[J].机器人,2002,24(5)：475-480．

[2] 卢恩超,张邓斓,宁雅男,等.改进人工势场法的机器人路径规划[J].西北大学学报：自然科学版,2012,42(5)：735-738.

[3] Yang S X, Luo C. A neural network approach to complete coveragepathplanning[J].IEEE Transactions on Syatems,Man and Cybernetics：Part B,2004,34(1)：718-724.

[4] GoerzenC,KongZ,Mettler B. A Survey of Motion Planning Algorithms from the Perspective of Autonomous UAV Guidance[J].Journal of Intelligentand Robotic Systems,2010, 57(1-4)：65-100.

[5] 董宇欣.移动机器人路径规划方法研究[J].信息技术,2006,30(6)：108-111.

[6] ColorniA,Dorigo M,ManiezzoV.Distributed Optimization by Ant Cnlnnies[A].Proceedings of the First European Conference 0nArtifial Life[C].1991：134-142.

[7] 王仲民.移动机器人路径规划与轨迹跟踪[M].北京：兵器工业出版社,2008.

[8] 黄健生.移动机器人的路径规划研究[D].浙江：浙江大学,2008.

[9] Khatib O. Real-time Obstacle Avoidance for Manipulators and MobileRobots[J].The International Journal of Robotics Research, 1986,5(1)：90-98．

[10] KoeingS,LikhachevM.Inproved fast replanningfor robot navigation in unknownterrain[A].2002 IEEE International Conf. on Robotics andAutomation,Washington[C].2002：968-975.

[11] Ke Liang, Zhiye Li,Dongyue Chen. Improved Artificial Potential Field for Unknown NarrowEnvironments[A].Proceeding of the 2004 IEEE International Conference on Robotics andBiomimetics, August[C].22-26,2004,688-692.

[12] 潘洲,万衡,李嘉琦.基于模糊人工势场法的移动机器人路径规划[J].制造业自动化,2015,