基于模型仿真技术的PID参数整定优化

郭 波，邹丽梅，钱学毅

GUO Bo, ZOU Li-mei, QIAN Xue-yi

（武夷学院 机电工程学院，武夷山 354300）

0 引言

PID控制通过调节比例P、积分I与微分D三个参数，分别与输出偏差值相乘，其代数和输入系统，从而调节系统输出响应，期望满足快速、准确和稳定的控制需求。PID控制算法历史悠久，简单可靠，参数物理意义明确，控制器容易实现，至今仍在工业控制中占统治地位。PID控制难点在于整定合适的PID参数值，许多场合仍采取人工整定参数的方式。目前许多设备的自动整定功能局限于整定过程的特定条件，且整定效果不够理想。利用智能优化算法实现PID参数的全局寻优是当前自动整定的一个发展方向，算法实现一般以编程模拟PID控制过程，求取误差积分准则的目标函数作为优化目标。

但工业应用中PID控制器种类繁多，控制目标与实现方式千差万别。程序模拟跟踪此控制过程，求取误差建立目标函数的难度较高。因此许多文献资料的算法仅测试最简化PID控制仿真，难以说明实际控制效果。MATLAB Simulink提供了动态建模仿真开发环境，是目前开发实际控制模型的最简单可行的方法。若目标函数程序设计用命令行仿真技术实现，建模过程可替代传统编程工作方法，使优化开发过程更为简便。若模型程序接近实际控制系统，优化的PID参数整定结果就可直接应用于实际工业控制过程。

1 设计PID控制模型

Simulink是一个面向多域仿真并和基于模型设计的框模块图环境，是MATLAB软件的扩展。用户可利用功能块化的模块搭接生成系统模型，不需编程就可完成系统的输入输出仿真，仿真输出值不仅可通过Scope模块（示波器）直接观察，还可输出至MATLAB工作空间中。

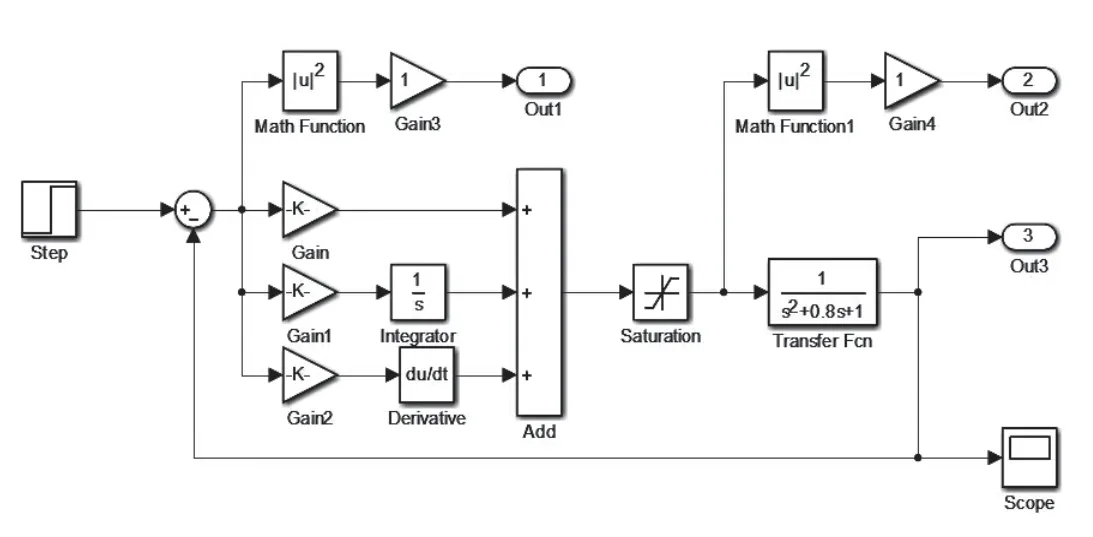
图1 PID控制模型

图中设计三个仿真过程数据输出，其中Out1模块输出系统仿真过程误差值的平方，Out2模块为经过限幅的控制值的平方，Out3模块为系统输出值。

Gain、Gain1、Gain2增益模块设置为PID控制参数整定对象的变量，并声明为MATLAB全局变量，便可接受多个M程序的数值调用。优化算法的优化对象即是此变量组成的向量。

实际控制系统虽然远比以上算例复杂，但实现模型中若干个参数的寻优原理是相同的，相对MATLAB自带的优化工具箱，该方法的寻优算法可根据需要选择。方法实现核心在于应用MATLAB的命令行仿真技术。

2 命令行仿真建立优化目标函数

2.1 命令行仿真函数

大多数控制算法与优化算法都需要目标函数比较控制优化效果，在MATLAB中通常用M文件编写。MATLAB提供了用于M文件的命令行仿真函数sim（），可实现在程序中调用模型动态仿真，其命令格式为：

参数model为仿真的模型文件名称，timespan为设置系统仿真的时间范围，可单设终止时间tFinal，也可设置起始时间、终止时间与时间间隔，如仿真时间20秒，仿真间隔0.01秒，仿真模型名为pid的命令为：

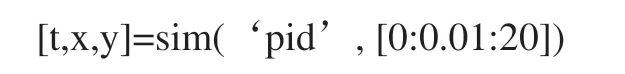
仿真间隔决定仿真耗费的时间与函数值计算工作量，但较大的时间间隔可能影响到优化结果的准确性。PID参数寻优过程可能使仿真产生大量过零，引起Simulink错误停止仿真，因此需要在Simulink参数选项中关闭过零错误。

输出矩阵t为仿真时间向量，x为仿真中间状态矩阵，按先连续状态后离散状态输出过程中间值，y为仿真输出矩阵，当模型有Out1至Out3的三个输出，y即为三列输出。对图1PID控制模型仿真后，y输出矩阵的第一列y(：,1)输出误差平方，第二列y(：,2)输出控制值平方，第三列y(：,3)输出系统输出值，目标函数所需数据可采用类似方式设置输出。

2.2 PID参数整定多目标函数设计

目标函数程序一般定义为M函数文件，方便在优化算法的M脚本文件中调用。PID优化向量在仿真前必须做全局变量声明。命令行仿真所获得的输出矩阵y提供了求取性能指标所需数据。

PID控制系统目标是使输出值y(：,3)的变化过程与期望过程尽量接近。系统的阶跃响应要接近输入的阶跃过程，按照不同的控制品质需求，有超调量、稳态误差、调节时间等多目标值。

许多技术文献将误差积分准则设置为优化目标函数。常见的有平方误差积分准则，缩写为ISE，准则形式为其中e（t）为实际输出或主反馈信号之间的偏差，目标函数可通过累加y(：,1)实现。

不同的准则提供不同的目标函数性能，基于ISE的性能着重于抑制过渡过程中的大偏差的出现，基于ISTE的性能指标在控制大偏差的同时还可缩短调节时间。但是任何误差积分准则均有局限性，不可能完全适应多样的实际控制需求。

经过反复PID参数优化比较，将组成误差积分准则的多个目标，如偏差e(t)、时间t、控制值y(：,2)、输出值y(：,3)、超调量、稳态误差等仿真结果组合构成单一目标函数适应度值。当偏差与控制值取100至0.01数量比值，输出值超调作为惩罚项，分别五次优化的取最优控制输出结果比较如图2所示。

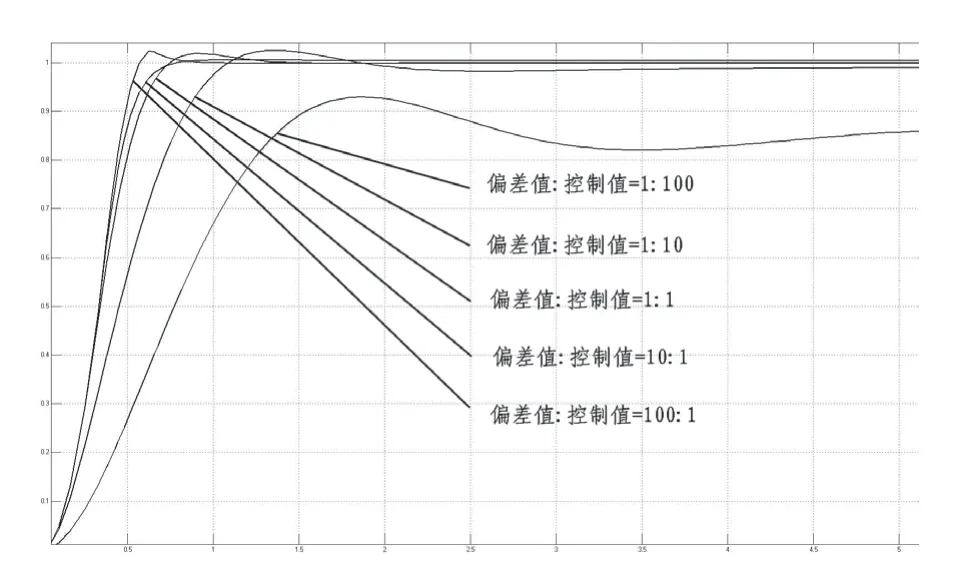
图2 权重数量级寻优结果对比

从结果曲线可看出，控制值决定系统的输入量改变与速度变化，实际系统的控制量不可能无限大，较小的控制量影响着系统能耗，控制值权重最大的曲线响应缓慢，稳态误差大。偏差值是最主要的指标量，决定了输出过程信号与期望过程的接近程度，偏差值权重最大的曲线出现了较陡的超调，以偏差为指标的优化结果将趋向高比例增益，强震荡的控制输出，反而有害。时间t与偏差e(t)相乘，可扩大稳态精度的影响。对优化过程比较分析，优化算法仅能根据适应度最小值使优化目标收敛，多目标误差积分准则影响着控制曲线的不同特性，当追求均衡的控制效果，必须设置数值为均衡的多目标误差积分，多目标权重比在10倍以内，即是使其累计数值处于同一数量级上下，PID控制曲线则可获得较满意的控制品质。

3 粒子群优化算法整定PID参数结果

粒子群优化算法(particle swarm optimization, PSO)是近年发展出的群智能优化算法，利用鸟群生物原理，模拟鸟群觅食的社会行为，基于迭代进行优化。MATLAB实现粒子群算法整定PID参数具体流程如下：

1）建立如图1的Simulink PID控制模型。

2）建立M函数文件fitness作为粒子群适应度函数。函数在命令行仿真后，设定目标函数为累加输出误差平方y(：,1)×权重值，累加控制值y(：,2)×权重值，累加输出值y(：,3)惩罚项。

3）初始化粒子群规模N=40，在可行域随机产生每一粒子的位置Xi和速度Vi，取权重初值为1，计算每一粒子适应度，初始化每个粒子个体极值Pi与全局极值Pg。计算极值粒子偏差值与控制值数量级，更改权重值调整至两者数量级相同。

4）迭代群体所有粒子，按照下面公式更新粒子的速度Vi和位置Xi。

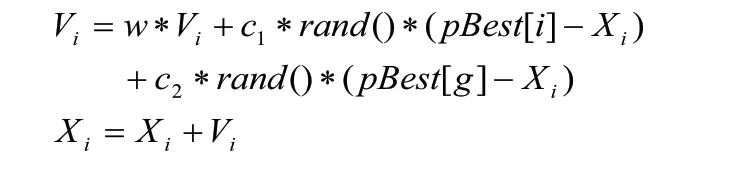
其中c1、c2为常数，称为学习因子；rand ()是[0，1]上的随机数；w是惯性权重(inertia weight)；pBest[i]为对应个体极值的粒子位置，pBest[g]为对应全局极值的粒子位置。

5）对更新后的粒子计算适应度，与粒子个体极值比较，若优于个体极值则替代最优个体位置，并更新个体极值。与粒子全局极值比较，若优于全局极值则替代全局极值位置，并更新全局极值。

6）当适应度值达到精度要求或迭代次数达到上限，则给出最优结果，否则迭代次数加1，跳回流程4）。

优化执行过程若打开了Simulink模型，则可实时观察优化后的仿真输出，可以明显观察到优化效果。针对图1PID控制模型，以40个粒子迭代100次，反复10次优化获得的PID参数如表1所示，最优的5个控制输出曲线如图3所示。可见整定参数后的PID控制有控制输出曲线调节时间小，超调量小，稳态精度高的特点，优化结果满足工程实践的整定需要。

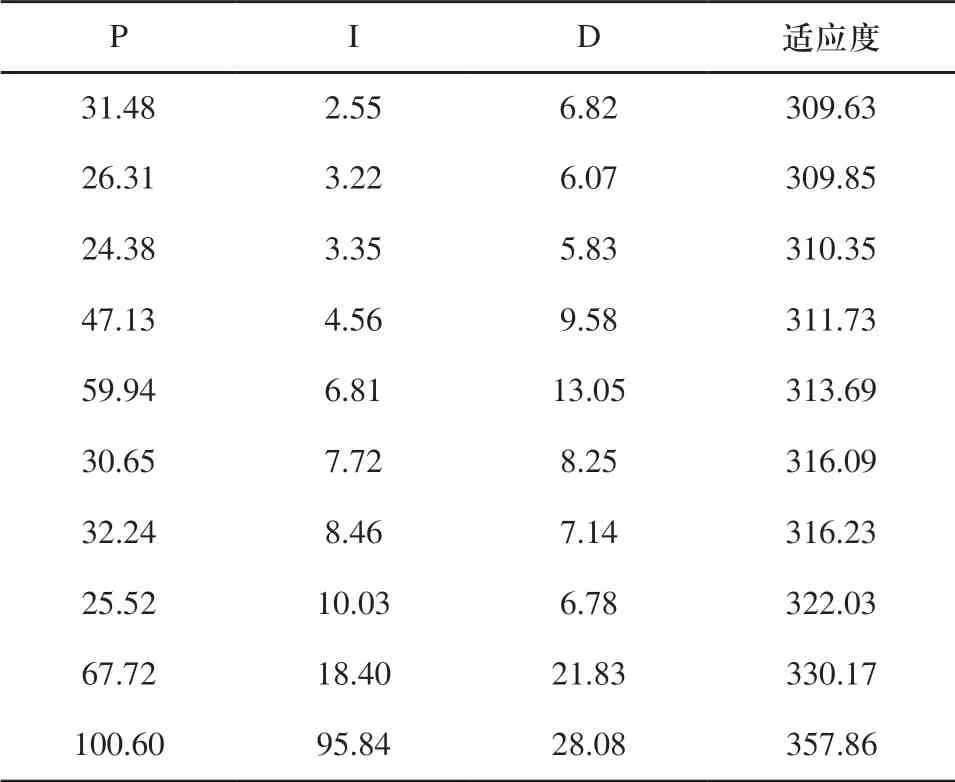
表1 PID控制模型参数整定结果

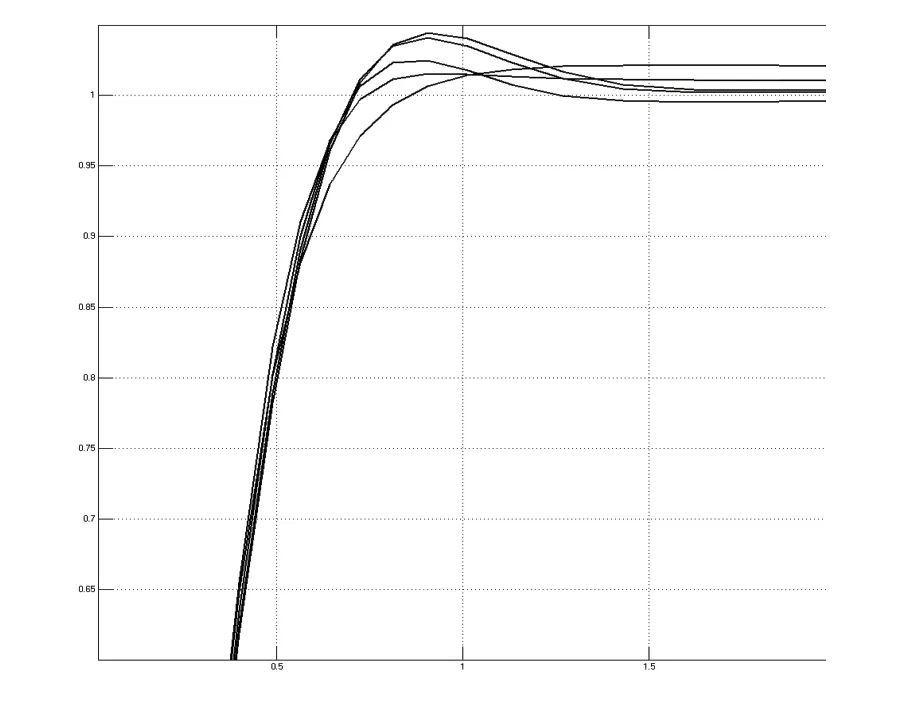
图3 仿真输出示波器结果

4 结论

随着计算机技术进步，仿真速度不断提升，使提取仿真数据，建立目标函数的误差积分准则的方法变得有效。基于模型仿真技术的PID参数整定优化具有简单、通用等特点，优化的重心将建立在模型的准确性与算法的选择上。

比较整定实验与仿真结果，利用优化算法整定PID控制器参数，依赖某一单独误差积分准则为目标函数，难以获得满意的优化结果。根据控制实际，设计误差积分准则构成，提取Simulink模型仿真输出矩阵，构建算法目标函数，通过粒子群优化算法对PID控制参数寻优，是一种有效的计算机辅助离线PID参数整定方法。

[1] 何晋元,周国鹏.用于控制器参数寻优的目标函数研究[J].微计算机信息.2006(07)：86-88

[2] 周国鹏,柳学坤,何晋元.基于控制系统优化的ITSE目标函数的研究[J].微计算机信息.2006(22)：46-47.

[3] Kennedy J, Eberhart R.Particle swarm optimization[A].IEEE International Conference on Neural Networks： Perth, Australia. Piscataway. NJ： IEEE Service Center[C].1995：1942-1948.

[4] Eberhart R,Kennedy J. A new optimizer using particle swarm theory[A].Roc. Sixth International Symposium on Micro Machine and Human Science： Nagoya, Japan. Piscataway,NJ： IEEE Service Center[C].1995：39-43.

[5] 张利彪.基于粒子群优化算法的研究[D].吉林大学,2004.

[6] 刘道.基于改进粒子群优化算法的PID参数整定研究[D].南华大学,2012.

[7] 李刚,王庆林.基于阶跃跟踪响应的PID控制器性能评价与调节[J].系统仿真学报.2008(14)：3763-3766.