基于主观赋权法的控制系统优化研究

洪 烽，曾智勇，周琬婷，郭楚珊

HONG Feng, ZENG Zhi-yong, ZHOU Wan-ting, GUO Chu-shan

（华北电力大学，北京 102206）

0 引言

控制系统的品质常从稳定性、准确性和快速性三个方面来评价，而随着控制系统的复杂程度以及用户对控制精度的要求日渐增高，不同的情况下决策者对稳定性、准确性、快速性的倾向程度又不同，仅凭经验或者简单的实验方法已无法确定满足要求，传统整定方法又比较复杂、耗时。最优理论的不断发展，为控制器参数的寻优提供了理论依据。在控制工程中，二阶欠阻尼系统的典型应用十分普遍，并且不少高阶系统的特性在一定条件下可用二阶系统的特性来表征。因此，本文着重研究二阶欠阻尼系统的控制参数优化。

文献[2]中利用离散相似法数字仿真获取控制系统的目标函数, 并利用单纯形法对调节器参数进行寻优, 改善了超调量和调节时间。文献[3]中利用单纯形法对基于“ISE”准则的目标函数进行了改进, 改进后的参数寻优对动态性能指标有一定的改善，但是最优的结果和工程实际有一定的误差。文献[4]中在MATLAB工具箱基于ITSE准则的目标函数的基础上，提出一种适用于控制系统参数寻优的新的目标函数，实现了对控制系统的时域性能指标的改善。但其整定系统的时域响应固定不变，不能满足不同系统对稳定性、快速性、准确性之间重要程度的不同倾向，无法灵活适应现阶段实际工程对复杂控制系统性能的要求。

本文在寻优思路的启发下，显式的利用控制系统超调量、上升时间、衰减率、调节时间等性能指标的加权组合作为目标函数，根据决策者对不同性能指标的倾向程度利用主观赋权法确定加权系数。故该方法在清晰地反映出系统控制精度的基础上，还可根据用户对控制性能的不同期望灵活的找出合适的控制参数。最后通过仿真证明该方法的有效性。

1 理论推导及算法实现

1.1 二阶系统对象的分析

在控制工程中，除了那些不容许产生振荡响应的系统外，通常都希望控制系统具有适度的阻尼、较快的响应速度和较短的调节时间。因此，二阶控制系统的设计，一般都需优化常用的方法是对对象进行零极点的配置来达到所期望的输入输出响应，对于二阶系统：

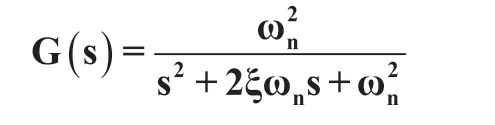
有：

而工程整定中常用衰减曲线法。该方法对于扰动频繁，过程进行较快的控制系统不适用，要准确地确定系统响应的衰减程度比较困难，且整定依靠经验公式，对于实际的复杂系统无法适应，整定过程繁琐且容易带来较大误差。

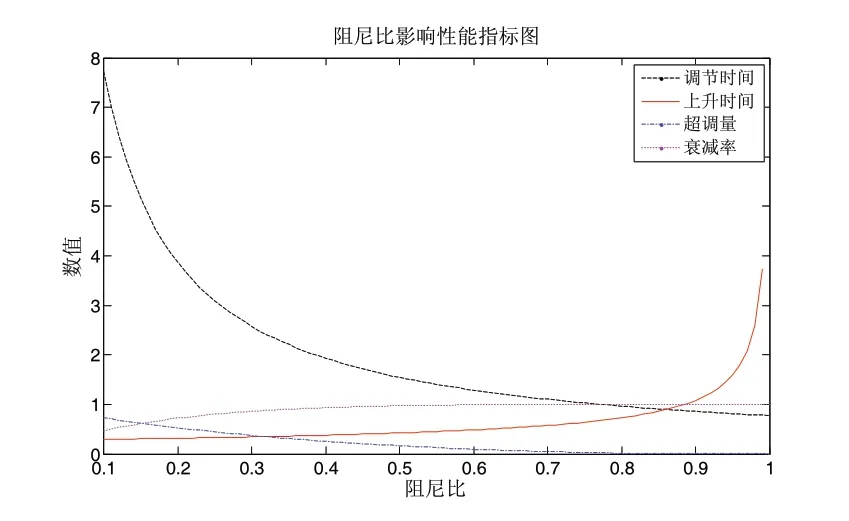
图1 阻尼比-性能指标图

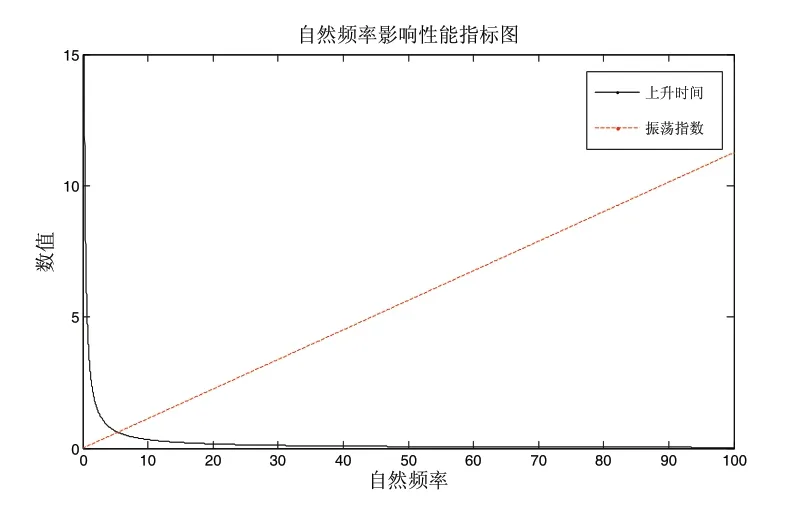
图2 自然频率-性能指标图

1.2 目标函数

由上一小节可知，控制系统常用的性能指标之间相互矛盾，而实际控制中往往存在决策者研究需要或条件限制，对不同的性能指标有不同的重视程度和要求等，有些极端情况下甚至可以在考虑满足研究需要的前提下放弃一些性能指标，故单纯得利用误差时间积分等准则作为目标函数不能体现出实际控制中复杂的情况。本文基于控制系统常用的性能指标和主观赋权法寻优的思想设计了针对二阶欠阻尼系统对象模型的目标函数：

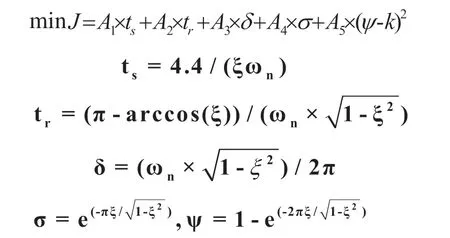
其中，A1,A2,A3,A4,A5分别为调节时间、上升时间、振荡指数、超调量、衰减率的主观权值，k值为期望的衰减率（工业过程中常取0.9）。

从表达式中可以看出，新的目标函数J显式的考虑了控制系统的各组性能指标，并可以调整各指标的重要程度。对将各指标数值进行无量纲归一化之后（下文均在此基础上变动主观权值），利用主观赋权法确定一组主观权值组，带入目标函数，即可进行各指标参数寻优。

1.3 “限制型”主观赋权法

主观赋权法是由决策者根据主观上对各指标的重视程度来决定权系数的一类方法。常见的有专家调查法、相对比较赋权法、连环比率法、关联树法、集值迭代法和特征值法等。主观赋权法由于基于决策者主观偏好或经验给出指标权重，体现了决策者的经验判断，权重的确定一般符合现实，所以解释性强，但其客观性偏弱。针对客观性偏弱的缺点，本文在主观赋权法（特征值法）的基础上对加权系数增加“限制”，来满足系统客观上对各个指标的最低限度。

在实际系统中，对稳定性、准确性、快速性的倾向程度由于决策者研究需要或条件限制不尽相同，本文将5个性能指标赋予权值即可量化这种倾向程度并将之体现在优化过程中，可以较为准确的整定出符合实际运行工况的参数，且实现快速、简单，可以用于复杂系统的在线整定。

1.4 遗传算法寻优

遗传算法是一种借鉴生物界自然选择和遗传机制的高度并行、随机、自适应的全局优化概率搜索算法。本文出于对全局最优以及实时性的考虑，利用实数编码的遗传算法对目标函数进行参数寻优。

2 仿真试验（Simulation）

基于主观赋权法目标函数的控制器参数寻优系统如图3所示。

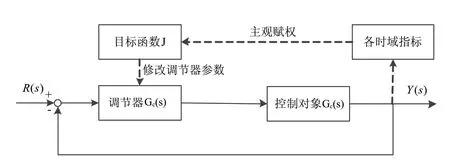
图3 控制器参数寻优图

首先根据用户对期望性能指标的不同要求给不同的权值，利用主观赋权法（特征值法）确定各个性能指标的主观权值，然后利用遗传算法对阻尼比和自然频率进行寻优，即能设计出更加适用于用户的控制器参数。

已知控制对象的传递函数为：

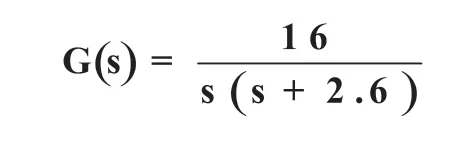
表1给出了几组典型的参考权值。其中标准权重组（即每个性能指标的重要性一样）得出的控制器为：

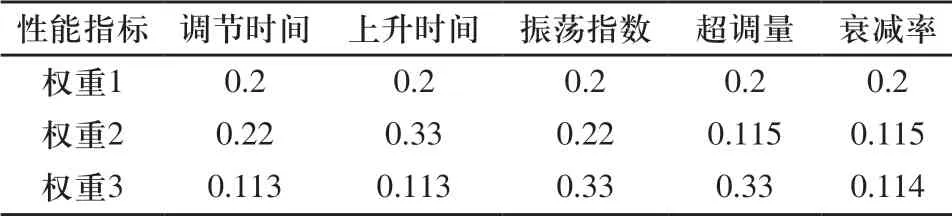
表1 典型参考权值

通过新的目标函数得到的参数组合如表2所示。

表2 典型参数组合

对表2中各组参数所得的控制系统进行单位阶跃响应，仿真结果如图4所示。

由图4可知，对象未优化时，系统的超调量为33.97%，调节时间为3.38s，曲线1（标准组）作为标准权重的阶跃响应，综合考虑了上升时间、超调量、调节时间等性能指标，此时系统的超调量为2.63%，调节时间为1.02s，大大提高了系统的快速性和准确性。而曲线2显然是把系统响应的快速性视为更加重要，即上升时间、调节时间的权重相对较大。曲线3则把系统响应的阻尼程度视为更加重要，即超调量、振荡指数的权重相对较大。由此可以看出，本文提出的新的目标函数可以十分灵活且有效的适应用户各种不同的要求而产生不同的控制参数组合。

图4 仿真结果图

3 结论

本文基于控制系统常用的性能指标和主观赋权法的思想设计了针对二阶欠阻尼系统对象模型寻优的目标函数，然后又用遗传算法对控制系统调节器的参数寻优。大量仿真实验表明该方法可以根据用户对各个时域性能指标重要性的倾向，灵活地对系统进行优化，优化设计后的系统各个性能指标都能得到改善，且能很好得适应用户研究需要或条件限制，具有一定的工程实际意义。

[1] 胡寿松.自动控制原理(第5版)[M].北京：科学出版社,2007.

[2] 王福永.单纯形法在控制系统调节器优化设计中的应用[J].苏州大学学报（工科版）：2002,22(4)：38- 41.

[3] 唐小艳,颜玉崇.用于参数寻优的ISE目标函数研究[J].福建电脑,2003,9：14.

[4] 周国鹏,柳学坤,何晋元.基于控制系统优化的ITSE目标函数的研究[J].微计算机信息,2006,22：46-47.