基于有限元模拟铝质易拉罐的罐底结构优化

林明山，林 娜，胡滨铠

LIN Ming-shan, LIN Na, HU Bin-kai

（漳州职业技术学院 机械与自动化工程系，漳州 363000）

0 引言

铝质易拉罐具有质轻、保质期长、防假冒性强、携带方便、可回收性好等优点，消费量逐年增长。受材料价格及市场竞争等因素的影响，降低成本是行业永恒的主题，而铝板材的减薄始终是重要课题。易拉罐用铝材占罐体成本约70%左右，板材厚度每减薄0.01mm，罐体可增产2.8%，其效益显而易见[1]。但材料厚度每减薄0.005mm都是一个艰难的级差，与冶金、化工、机械、电子等诸多行业的技术进步紧密关系。

美国是易拉罐发源地及消费大国，60年代用的罐材厚度为0.45mm，之后不断利用相关行业的技术进步进行材料减薄研究，90年代后期减薄至0.270mm，现已减至0.250mm。中国易拉罐生产始于八十年代初期，该时期生产用的板材厚度为0.351mm。因引进生产线时设备工装使用的材料厚度规格在上限，为板材的减薄留下空间，罐厂通过对引进的设备工装技术进行消化，结合生产经验积累实现了减薄至0.300mm的目标。之后，业界根据二十多年积累的经验实现减薄到0.285mm的跨越。从0.351mm减薄至0.285mm的进程中，技术瓶颈是薄板材的变薄拉伸技术及减薄后的确保罐体轴向压力问题。随着材料厚度继续减薄至0.280mm时，则开始出现罐底耐压强度低于产品性能要求的问题，成为材料厚度减薄进入新的拐点。因此，进行这方面的研究具有较高的应用价值。

1 罐底耐压力的有限元模拟

图1是用于0.351mm板材厚度的罐底结构（主要参数如表1所示），多次材料厚度减薄直至0.285mm时，一直沿用这个结构，在此厚度规格下生产的产品未出现耐压力不能满足产品性能要求的问题，继续减薄至0.280时，该厚度规格生产的产品经检测，有些产品出现耐压力低于指标值。

罐底的强度主要取决于材料的性能、材料厚度、罐底结构以及金属的变薄程度。在这些因素中，材料性能的改进牵涉面广，难于实现。可行的办法是进行罐底结构优化。

用传统的试模方法进行罐底结构优化，这种方法是按经验值选取，然后根据试模结果进行修正，存在设计周期长、试模次数多、生产成本高等缺点。用有限元方法，则可以克服上述缺点，比较准确地预测铝合金板料罐底成形后的耐压力情况，为生产实践提供重要指导[2]。

根据图1参数进行三维造型，利用ALGOR有限元分析软件就材料厚度减薄至0.280mm的底部耐压强度进行模拟分析，找出影响罐底耐压力的关键结构参数，然后结合罐底成形工艺，优化设计出新的罐底结构。

本研究采用的铝合金板材规格与目前罐业使用的3104H19一致，该材料是在原使用的3004H19基础上进行改进，其化学成分中除了增加硅和铁的比重外还增加了0.10%的钛和0.05%的钒，以增加材料的强度和延伸率[3]，对材料减薄后的罐体成形有较好的工艺适应性。

根据铝材供应商提供给罐厂的材料技术指标表明，3104H19铝合金板材的机械性能指标，屈服强度Re≥255Mpa，抗拉强度Rm≥295Mpa[4]。有研究表明，罐体铝合金材料在加热时发生软化, 经常规烘烤处理后（200oC烘烤7分钟后）强度下降8%～10%[5]。因罐厂在制造罐体时，根据生产工艺需要罐体拉深后经三次常规烘烤处理，温度上限达到200oC。因此，材料减薄后应考虑常规烘烤处理对罐底部耐压力产生的影响。据此，罐体制造后材料实际的屈服强度Rm为235Mpa～225Mpa，要确保罐体质量稳定性则Rm的指标取225Mpa为依据进行分析较为可靠。

对弹塑性材料采用弹塑性有限元分析变形时，假设材料满足以下条件， 即材料体积不可压缩，材料均质且各向同性[6]。根据罐业国家标准，罐底耐压力≥610Kpa[7]。据此，与生产实验方法相同，约束设置在罐口，对罐内施加610KPa的压力。模拟结果表明，作用在罐底内侧壁红色标示处的等效应力σe最大值为229.25Mpa，如图2所示。根据Von Mises屈服准则，在一定的变形条件下，当受力物体内一点的等效应力达到某一定值时，该点就开始进入塑性状态[8,9]。因此，对于塑性材料，受力物体在任何一点的等效应力都应小于屈服强度。因235＞σe＞225Mpa，在生产过程中罐体的常规烘烤处理的温度，如果控制在上限200oC以下，则本结构适用0.280mm板材生产。由于生产过程中烘烤处理的温度不是恒定值，在上限运行期间，罐体最大等效应力为229.25Mpa，大于铝材的实际屈服强度（225Mpa），该罐底结构会发生屈服变形。因此，本结构使用0.280mm厚度板材生产出的罐体耐压力有不稳定性，与生产实践一致。由此可见，材料减薄至0.280mm时候，罐底耐压力进入一个拐点，若要材料减薄要继续下去，则必须解决这个问题。

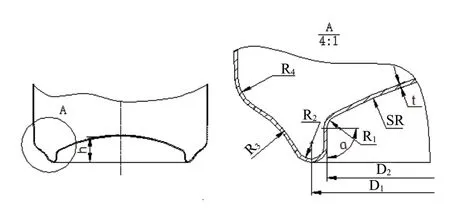
图1 0.32mm板厚的罐底结构

表1 原有罐底结构尺寸参数

2 罐底结构优化的关键参数

罐底是采用反向拉伸工艺形成的反向拱型，成形发生在拉伸凸模的行程终点，因成形底部所需材料直径拉伸时会产生起皱，该成形采用强力反向压边的模具结构使底部成为胀形成形，克服了起皱的问题，可以忽略材料减薄后对罐底成形的影响。底部成形时考虑到金属的成形性能，根据实践，罐底沟内壁圆角R2应大于3倍的材料厚[10]，不过取值太大会影响强度应加以考虑；球面与罐底沟内壁圆角R1应大于或等于3倍的材料厚t。

图2 优化前用于0.280mm板材厚度的罐底等效应力情况

工艺研究表明，α与罐底强度关系密切，取值时应考虑R1对下道工序的影响及模具结构的复杂性。当90°≤α≤95°时，罐底易成形不会影响脱模，且罐底球面和侧壁连接处的圆弧R1有较好的强度，是一个合理值；对于R1的取值， R1常取（4～5）t。材料越薄则罐底球面成形时容易产生回弹，采用多段曲面光滑连接，可以有效解决这个问题。此外，在R3设计一个与水平夹角为α1的倾斜面代替部分圆弧，将有效增强整体强度，但α1取值太小，会大大减小罐底耐压能力，又因罐体成品是堆垛捆扎，要考虑罐底与罐口堆叠要求，α1取值又不能太大，综合考虑28°≤α1≤50°是一个合理值，α1应与β的取值应相适应。除此之外，加大罐底部反向成型的高度h也是提高罐底部强度的一个好措施，但h值不宜太高，否则会使底部材料产生二次延伸，降低强度。

根据有限元模拟分析得知，在罐底内侧壁红色标示处的等效应力σe最大，此处应作为优化的关键点，找出影响耐压力的罐底结构参数，这些参数主要有基本尺寸D1、D2，拱形高度H、球面SR及R1、R3。他们之间存在如下关系：材料越薄，应适当减少D1及D2尺寸以缩小球面面积有利于增强球面耐压力。结合罐底成形工艺，给出图3优化后用于0.280mm板材厚度的罐底结构（主要参数如表2所示）。

图3 优化后的罐底结构

表2 优化后的罐底结构尺寸参数

3 试验

3.1 模拟试验

经优化后的罐体就罐底耐压力进行再一次模拟，图4显示了罐体内部在610kPa的压力作用下，作用在罐底的等效应力σe最大值为218Mpa，因σe＜225Mpa，罐体最大等效应力小于铝材的实际屈服强度。由此得知，优化后的罐底结构满足耐压力要求。在生产过程中严格控制烘烤处理的期间温度，本结构使用0.280mm厚度板材生产出的罐体耐压力具有稳定性。

把优化后的罐底结构用于分析使用0.275mm、0.270mm板材厚度的耐压力情况。模拟结果得知：用于0.275mm板材厚度时，作用在罐底等效应力σe最大值为224Mpa，如图5(a)所示。因σe＜225Mpa，由此得知本结构也适用0.275mm厚度板材；用于0.270mm板材厚度时，作用在罐底等效应力σe最大值为232Mpa，如图5(b)所示。因235＞σe＞225Mpa，本结构适合0.270mm板材生产，但生产出的罐体耐压力有不稳定性。

图4 优化后用于0.280mm板材厚度的罐底等效应力情况

图5 优化后用于其他板材厚度的罐底等效应力情况

3.2 生产试验

把优化后的用于0.28mm板厚的罐底结构制成模具，在某制罐公司引进的高速易拉罐自动化生产线上进行0.28mm、0.275mm、0.270mm三种板厚的罐体生产试验。随机各抽取10只样件，根据国标要求的测试方法，在最小读数不大于1Kpa的罐底强度测试仪检测，读取罐底部变形时的最大读数[7]。采用行业专用的罐底部耐压力测试仪ALTEK9200，约束设置在罐口处，对罐内施加610KPa的压力，结果表明用于0.28mm、0.275mm板厚生产的产品，本组数据均大于610Kpa，罐底的耐压力满足罐业国家标准。而用于0.270mm板厚生产的产品，本组数据中8个大于610Kpa，1个小于610Kpa，罐底的耐压力出现不稳定，试验结果与有限元分析相一致。

4 结论

材料的厚度和强度是一对矛盾而又与成本关系密切。料减薄至0.280mm时候，采用原有的罐底结构生产出来的罐底耐压力存在不稳定性，已不能满足产品质量要求，若要继续减薄材料厚度，必须解决这个问题。利用有限元模拟可以比较准确地预测铝合金板材减薄后，成形的罐底的耐压力情况，并找出材料减薄后影响罐底耐压力的主要罐底结构参数，然后结合罐底成形工艺要求设计出新罐底结构，克服设计周期长、试模次数多、生产成本高等缺点，这是优化罐底结构，提高罐底耐压力可行的方法，为生产实践提供重要指导。

[1] 林明山.降低成本是国产易拉罐发展的必然趋势[J].轻合金加工技术,1999,6：34-39.

[2] 曾绍锋,陈文哲,等.有限元模拟用于优化镁合金板碟形拉深成形的模具参数[J].塑性工程学报,2010,4：58-61.

[3] 韩向东,李志见.铝质易拉罐轻量化技术探讨[J].轻工机械,2003,4： 29-32.

[4] Alcoa Product Date Rigid Container Sheet[S].Aliuminum Company of Ameica,1992,7：5-6.

[5] Ghosh S K. Developments in the drawing of metals[J].Journal of Mechanical Working Technology,1985,11(2)：246.

[6] 王焕定.有限单元法基础[M].北京：高等教育出版社,200l.

[7] GB/T 9106-2001包装容器铝易开盖两片罐[M].北京：中国标准出版社,2001.

[8] 王平,崔建忠,金属塑性成形力学[M].北京：冶金工业出版社,2006.

[9] Takuda H, Mori K, Masuda I, et al. Finite element simulation of warm deep drawing of aluminum alloy sheet when accounting for heat conduction[J].Mater Proc Techn, 2002,(120)：412.

[10] 林明山.3104铝合金罐用板材减薄技术研究[J].轻合金加工技术,2013,5：58-62.