一深水钻机集成监控系统可靠性冗余优化

王鸿雁, 肖文生,2, 刘 健, 王逢德, 侯 超, 崔俊国

(1.中国石油大学机电工程学院,山东青岛 266580; 2.中国石油勘探开发研究院,北京 100083)

一深水钻机集成监控系统可靠性冗余优化

王鸿雁1, 肖文生1,2, 刘 健1, 王逢德1, 侯 超1, 崔俊国1

(1.中国石油大学机电工程学院,山东青岛 266580; 2.中国石油勘探开发研究院,北京 100083)

深水平台钻机集成监控系统(DSDR-IMCS)采用冗余方法提高可靠性,但存在费用、重量、体积等增加的问题。对DSDR-IMCS进行分析,建立一种适于DSDR-IMCS的可靠性冗余优化配置模型,提出一种基于模拟退火算法的PSO-GA混合算法对模型进行求解,该方法将PSO算法收敛快和GA算法全局收敛性好的优点相结合,引入模拟退火优化机制,并对PSO算法产生的新粒子群进行修正。结果表明,本文算法既可加快运算速度,降低计算强度,提高搜索效率,又可避免收敛过快陷入局部极大而降低全局搜索能力,且得到的优化结果更好,为DSDR-IMCS可靠性分析和设计提供参考。

集成监控系统; 可靠性; 冗余; 优化配置; 模拟退火; PSO-GA

深水平台钻机集成监控系统(integrated monitoring and control system of DSDR, DSDR-IMCS)控制要求高、规模大、逻辑复杂、平台空间有限,且故障或维护工作引起的停机代价是陆地钻机的数十倍,因此其安全可靠性要求更高。DSDR子系统往往来自不同的厂家,进行 DSDR-IMCS冗余优化配置研究对优化总体设计、提高集成监控效能、系统可靠性和经济性有重要意义。现代设计中通常采用高可靠性的产品或者冗余技术提高系统的可靠性。然而,高可靠性的产品受技术水平的限制,冗余技术却增加了系统的成本、重量、体积等资源[1-3]。笔者提出一种基于模拟退火算法的 PSO-GA 混合算法求解 DSDR-IMCS 可靠性冗余优化配置问题。

1 模 型

1.1 DSDR-IMCS分析

DSDR-IMCS的总体结构如图1所示。从上到下依次为远程监控层、司钻集中监控层、本地控制层和远程I/O层,各层设备的功能各有侧重,互相协调配合,完成DSDR-IMCS的全部功能。为了简化DSDR-IMCS的可靠性模型,仅考虑是否能完成DSDR-IMCS功能,并与实时数据相关系统组件,如实时服务器、操控台、控制器、交换机的可靠性,而不考虑打印机、摄像头、历史服务器等设备的可靠性。

图1 DSDR-IMCS的总体结构Fig.1 Overall structure of DSDR-IMCS

将DSDR-IMCS简化如下:远程监控层的各个监控子站和司钻集中监控室的数据服务器均通过选用更高可靠度的元件来提高其可靠性,不必进行冗余设计;但一级交换机-1、一级交换机-2、服务器、操控台、控制器、二级交换机采用冗余设计,可将这些组件看作并联冗余后串联构成,6种组件冗余个数分别为y1、y2、y3、y4、y5、y6;本地控制层和远程I/O层由多个子系统组成,任何一个子系统的失效都会使整套钻机无法正常工作,因此,可以将这些子系统看作串联结构,假设子系统个数为j,每个子系统分别包含二级交换机、控制器、远程I/O,冗余个数分别为y3j+4、y3j+5、y3j+6,简化后的结构简图如图2所示。

图2 DSDR-IMCS简化结构Fig.2 Simplified structure of DSDR-IMCS

1.2 模型假设

采用增加组件的冗余数提高系统的可靠度,在进行可靠性冗余优化设计之前先对系统进行假设:①采用的冗余均为主动冗余,且冗余组件与原组件完全相同;②每个子系统相互独立,且不可维修;③每个子系统有两个状态,即工作和失效2个状态;④每个子系统的可靠度为常数,且相互独立、互不影响;⑤每个组件的资源占有量对总资源来说是可分离的;⑥每个组件至少有两种不同参数可供选择。

1.3 数学模型建立

DSDR-IMCS的冗余配置方案采用可靠度高的并串联结构。并串联结构系统的可靠性冗余优化问题可以描述为:一个由n个子系统串联构成的系统,在满足总造价、总质量、总体积的约束条件下,寻找最优的组件x1,x2,…,xn及其冗余数yx1,yx2,…,yxn使其可靠度Rs最高。

假设第i个子系统单个组件编号为xi的可靠度为ri,第i个子系统冗余组件的数目为yxi,第i个系统的可靠度记为Ri(yxi)(i=1,2,…,n)。由于采用并联冗余,故Ri(yxi)=1-(1-ri)yxi,则该并串联结构系统的可靠度为

(1)

该并串联系统的可靠性冗余优化模型为

Y=max(Rs).

(2)

li≤yxi≤ui,i=1,2,…,n.

式中,gik(yxi)为yxi个组件在第i阶段所消耗的资源k的量;bk为资源k的最大量。

此问题转化为求一个有2n个变量、k个约束条件的目标函数值最大的解。

2 基于模拟退火的PSO-GA混合算法

2.1 算法策略

上述模型是一个带非线性约束的非线性多参数多极值整数规划的复杂问题[4-5]。采用GA算法求解该问题则搜索效率低,采用PSO算法则局部早熟或死循环问题严重[6]。鉴于PSO算法和GA算法有互补的优势,将两者结合起来,研究出性能更优的算法[7]。

目前两者结合的方式主要有两种:一种是将GA算法的基本操作引入PSO算法,改善PSO算法的性能。Angeline等[8-9]引入选择机制改进PSO算法,能够加速收敛速度,但搜索能力下降。Arumugam等[8,10]在PSO算法中引入了变异操作,一定程度上提高了收敛性能,但不能改变PSO算法的本质特征。

另一种方式则是将两种算法以同等地位进行混合[8,11-15]。目前从已提出的一些混合算法中可以总结出串联[8,16-17]和并联[8,11-12,15]两种主要的混合方式。若采用相同的种群规模和迭代次数,串联的计算量比并联多一倍;在搜索能力方面,无论是串联还是并联,都比单一的PSO算法或者GA算法要强。但PSO算法和GA算法处于同等地位,两者之间分工不明确,各自的优势没能得到充分发挥。

为此,本文中提出了一种基于模拟退火的PSO-GA的混合算法。采用PSO算法提高个体性能,采用GA算法得到更优秀的个体,利用模拟退火的优化机制,通过赋予搜索过程一种时变和最终趋于零的概率突变性来避免陷入局部极大而达到快速收敛到全局最优解的目的[7]。

2.2 算法设计

2.2.1 混合编码

DSDR-IMCS组件的属性包括组件的编号x、冗余个数y、价格C、质量W、体积P五个方面。基因组i可表示为(xi,yi,Ci,Wi,Pi)。则整个DSDR-IMCS组件的染色体可表示为

X=[(x1,y1,C1,W1,P1),(x2,y2,C2,W2,P2),…,(xn,yn,Cn,Wn,Pn)].

(3)

式中,n为组件的总个数。

2.2.2 适应度函数

目标函数是求最大值,所以DSDR-IMCS的可靠性的适应度函数定义为

(4)

约束条件

式中,Csum、Wsum、Psum分别为DSDR-IMCS各组件的总价格、总质量、总体积;gi1(X)、gi2(X)、gi2(X)分别为第i个组件的总价格、总质量、总体积。

2.2.3PSO优化参数

PSO算法采用常数学习因子c1和c2及常惯性权重w更新自己的速度和位置。

vi,j(t+1)=wvi,j(t)+c1r1[pi,j-xi,j(t)]+c2r2[qi,j-

xi,j(t)].

(5)

xi,j(t+1)=xi,j(t)+vi,j(t+1),j=1,2,…,d.

(6)

式中,t为迭代次数;r1和r2为0～1的随机数;pi,j为当代第i个粒子的最优解;qi,j为全局最优解;d为搜索空间的维数。

2.2.4GA优化参数

GA算法一般按照一定的交叉概率Pc和变异概率Pm产生新的个体。由于每个组件位置的选择和冗余个数影响整个IMCS的价格、质量、体积,因此对组件位置和冗余个数进行选择、交叉和变异。

(1)选择。采用轮盘赌方法,选择用于保留的最优个体,个体适应度值越大,被选择的概率越大。

(2)交叉。采用单点交叉法。

(3)变异。采用实值变异法。

2.2.5 模拟退火算法优化参数

采用模拟退火算法中的Boltzmann生存机制,在不增加群体数量的基础上,保持群体的多样性。模拟退火算法先设定初始温度T0和降温速率q,根据结束温度Tend进行终止。设新产生个体的适应度值为f,变动的阈值为fv,当f>fv时,接受新个体;否则,以一定概率P=exp((f-fv)/T0)接受新个体。

算法收敛准则:①迭代次数达到设定值。②连续多次迭代的适应度值无明显变化。

迭代满足收敛准则时,认为结果已收敛,停止迭代。

2.2.6 优化算法流程

求解过程如图3所示。

图3 基于模拟退火的PSO-GA混合算法流程Fig.3 Procedure of PSO-GA with SA

包括以下步骤:

①初始化基本参数,置群体代数Gen=1;

②判断是否满足终止条件,若满足,则转步骤⑥,否则,产生规模为N的初始粒子群,计算每个个体的适应度fit;

③采用PSO算法对粒子群进行优化并经修正操作后产生的新粒子群作为GA的初始种群;

④利用GA算法和模拟退火算法对种群进行优化,产生新的种群;

⑤判断是否满足收敛条件,若满足,则转步骤⑥,否则,Gen=Gen+1,进行新一轮迭代,转步骤②;

⑥计算并输出最优解,结束。

3 算例分析

假设子系统个数为8,则DSDR-IMCS的可靠性冗余优化问题简化为30阶段并串联系统的冗余分配问题,最大可靠度的适应度函数为

(7)

假设DSDR-IMCS设备的体积、成本、质量分别满足以下约束条件:

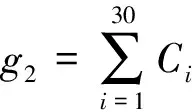
(8)

式(8)最早由Tillman提出[16-18],并在可靠性优化问题中被广泛采用[19-21]。

假设每个阶段的组件均有4种可供选择,并且组件的冗余个数最大值为4,DSDR-IMCS设备的总体积、总成本、总质量的最大值为560、730、960。

参照文献[4]中设计数据,DSDR-IMCS冗余单元的设计数据如表1所示。

分别利用本文算法、PSO算法、GA算法及PSO-GA算法对DSDR-IMCS的可靠性冗余优化分配问题进行测试,计算在IntelCorei5-2400CPU3.10 GHz,内存4.00 GB的计算机上执行。利用Matlab软件编程,经过大量的运算,各算法的参数设置如表2所示。为避免PSO算法早熟或进入死循环,对PSO算法产生的新粒子群进行修正,本文的修正方法是:先对产生的冗余个数进行四舍五入取整,若yi>5,则令yi=5;若yi<1,则令yi=1。

每种算法分别随机运行300次,运算得到各算法的平均可靠度值Rs,最大可靠度值Rmaxs,最小可靠度值Rmins,可靠度方差S,每次运算时间t,收敛代数Gen,早熟或死循环的概率,结果性能对比如表3所示,优化结果如表4所示。

表1 冗余单元设计数据

表2 算法参数设置

表3 算法结果对比

表4 算法优化结果

表5 带附加约束条件1的算法结果对比

表6 带附加约束条件1算法的优化结果

表7 带附加约束条件2的算法结果对比

表8 带附加约束条件2算法的优化结果

由表3、5、7可以看出:PSO算法得到的平均可靠度值最大、可靠度方差最小,但运算时间是本文算法的2～7倍,并且易早熟或进入死循环;GA算法的运算速度最快,但搜索效率低;PSO-GA算法比PSO算法的运算速度快,但仍没有解决PSO算法易陷入局部早熟或死循环的问题,也未解决GA算法的后期搜索效率低的问题;本文算法解决了早熟或死循环问题;本文算法的可靠度方差比PSO-GA略大,运算时间比PSO-GA算法略大,收敛代数比PSO-GA算法略慢,这都是由于本文算法以一定的概率接受差解,使得搜索范围更广,从而进化代数增加造成的。本文算法的收敛代数比PSO-GA算法大,表明PSO-GA算法结束进化后,本文算法的适应度函数值还在继续变化,不断寻求更优解;虽然本文算法的迭代次数有所增加,但在时间上的体现并不明显,相对来说求解效率依然很高;添加附加约束条件使早熟或死循环的概率增大,这是因为附加条件使得初始种群的适应度值更优,经过PSO算法和GA算法运算后不易得到满足约束条件的适应度值更高的个体。

从表4、6、8可以看出:每种算法优化得到的结果中元件的位置不能完全确定,这是由于该问题属于多极值问题,优化得到的结果不是唯一的;冗余个数是可以确定的,可靠度低的元件的冗余个数为3,例如控制器、操控台,而可靠度较高的控制器的冗余个数为2;这种优化结果是实际工程上需要的,同时也说明了本文优化算法的合理性和有效性。

表3、5、7对应的各种算法迭代300代,每种算法分别随机运行100次,得到的最优解如表4、6、8所示,得到的平均适应度函数曲线如图4所示。

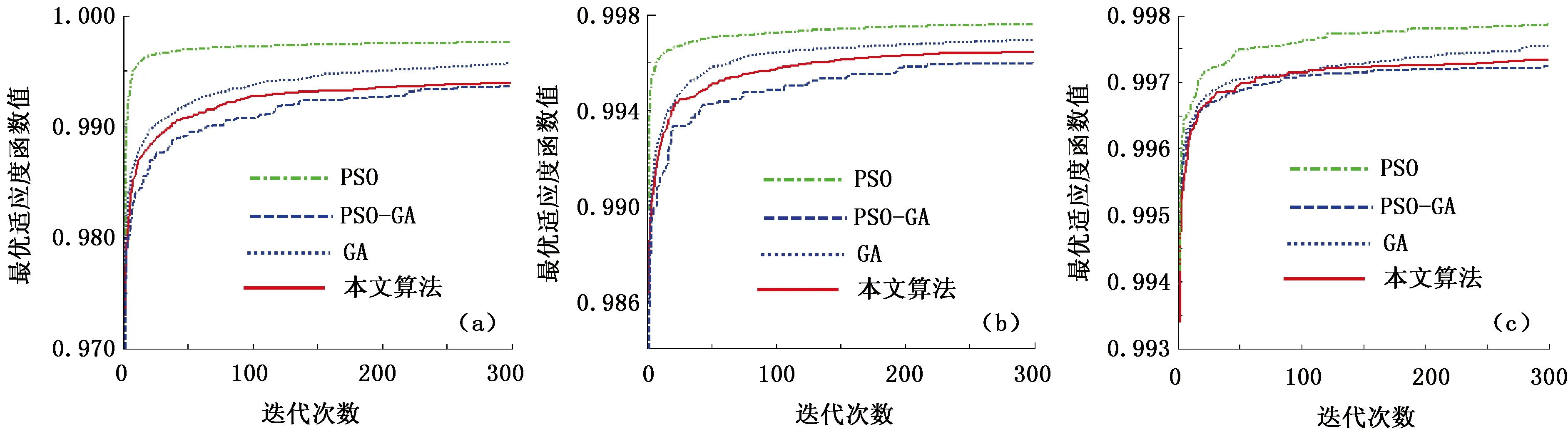
图4 各算法的适应度函数收敛曲线对比Fig.4 Convergence curves comparison of fitness functions

由图4可知,PSO算法收敛速度最快,得到的适应度函数值最大;GA算法后期搜索效率低;PSO-GA算法仍没有解决GA算法的后期搜索效率低的问题;本文算法对PSO算法产生的新粒子群进行修正,解决了早熟或死循环问题,后期搜索效率得到了改善。添加了附加条件的适应度函数值的初始值更大,收敛速度更快,可靠度方差小,运算结果更优。

4 结束语

针对DSDR-IMCS的可靠性冗余优化分配问题,建立了一个较完整的冗余优化分配模型,提出了一种基于模拟退火算法的PSO-GA混合算法。该方法既可加快运算速度,避免早熟和进入死循环,又可以避免收敛过快陷入局部极大而降低全局搜索能力。本文算法在得到近似最优解的同时,大大缩短了计算周期,降低了计算强度,提高了搜索效率,可以有效地解决DSDR-IMCS可靠性冗余优化配置问题。

[1] 任庆生,叶中行,曾进.基于实数型遗传算法的电子系统可靠性最优分配[J].通信学报,2000,21(3):43-46. REN Qingsheng, YE Zhongxing, ZENG Jin. Reliability computation of electronics system by real-valued genetic algorithm [J]. Journal of China Institute of Communications, 2000,21(3):43-46.

[2] DAVID W C, ALICE E S. Reliability optimization of series-parallel systems using a genetic algorithm [J]. IEEE Transactions on Reliability, 1996,45(2):254-260.

[3] 廖雯竹,潘尔顺,奚立峰.基于Tabu搜索和蚂蚁算法的系统可靠性分析[J].上海交通大学学报,2008,42(8):1291-1295. LIAO Wenzhu, PAN Ershun, XI Lifeng. Reliability analysis of system based on Tabu search and ant algorithm [J]. Journal of Shanghai Jiaotong University, 2008,42(8):1291-1295.

[4] TAVAKKOLI-MOGHADDAM R, SAFARI J, SASSANI F. Reliability optimization of series-parallel systems with a choice of redundancy strategies using a genetic algorithm [J]. Reliability Engineering and System Safety, 2008,93(4):550-556.

[5] 戴永寿,牛慧,彭星，等.基于自回归滑动平均模型和粒子群算法的地震子波提取[J].中国石油大学学报:自然科学版,2011,35(3):47-50. DAI Yongshou, NIU Hui, PENG Xing, et al. Seismic wavelet extraction based on auto-regressive and moving average model and particle swarm optimization [J]. Journal of China University of Petroleum (Edition of Natural Science), 2011,35(3):47-50.

[6] 史玉才,管志川,朱宽亮，等.大型丛式井组井口分配模型及其自适应遗传算法[J].中国石油大学学报:自然科学版,2012,36(6):70-73. SHI Yucai, GUAN Zhichuan, ZHU Kuanliang,et al. Wellhead allocation model for large scale cluster well and its self-adaptive genetic algorithm [J]. Journal of China University of Petroleum (Edition of Natural Science), 2012,36(6):70-73.

[7] 李敬花,余峰,樊付见.基于遗传模拟退火融合算法的船舶分段装配序列优化[J].计算机集成制造系统,2013,19(1):39-45. LI Jinghua, YU Feng, FAN Fujian. Ship block assembly sequence optimization based on genetic simulated annealing algorithm [J]. Computer Integrated Manufacturing Systems, 2013,19(1):39-45.

[8] 金敏,鲁华祥.一种遗传算法与粒子群优化的多子群分层混合算法[J].控制理论与应用,2013,30(10):1231-1238. JIN Min, LU Huaxiang. A multi-subgroup hierarchical hybrid of genetic algorithm and particle swarm optimization [J]. Control Theory & Applications, 2013,30(10):1231-1238.

[9] ANGELINE P J. Using selection to improve particle swarm optimization: IEEE International Conference on Evolutionary Computation-Proceedings[C]. New York: IEEE, c1998:84-89.[10] SENTHIL A M, CHANDRAMOHAN A, RAO M V C. Competitive approaches to PSO algorithms via new acceleration co-efficient variant with mutation operators [C].Los Alamitos: IEEE, c2005:225-230.

[11] JUANG C F. A hybrid of genetic algorithm and particle swarm optimization for recurrent network design [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2004,34(2):997- 1006.

[12] KAO Y T, ZAHARA E. A hybrid genetic algorithm and particle swarm optimization for multimodal functions [J]. Applied Soft Computing, 2008,8(2):849-857.

[13] LI Shutao, WU Xixian, TAN Mingkui. Gene selection using hybrid particle swarm optimization and genetic algorithm [J]. Soft Computing, 2008,12(11):1039-1048.

[14] MARINAKIS Y, MARINAKI M. A hybrid genetic-particle swarm optimization algorithm for the vehicle routing problem [J]. Expert Systems with Applications, 2010,37:1446 -1455.

[15] KUO R J, SYU Y J, CHEN Z Y, TIEN F C. Integration of particle swarm optimization and genetic algorithm for dynamic clustering [J]. Information Sciences, 2012,195:124-140.

[16] 郭威,等.最优可靠性设计:基础与应用[M].郭进利,阎春宁,译.北京:科学出版社,2011.

[17] 蒂尔曼,黄清莱,郭威.系统可靠性最优化[M].刘炳章,译.北京:国防工业出版社,1988.

[18] 黎放,朱承,王威.冗余系统费用模型及优化[J].系统工程与电子技术,2000,22(9):84-89. LI Fang, ZHU Cheng, WANG Wei. Cost models and optimization of redundant system [J]. Systems Engineering and Electronic, 2000,22(9):84-89.

[19] ZHANG Enze, WUN Yifei, CHEN Qingwei. A practical approach for solving multi-objective reliability redundancy allocation problems using extended bare-bones particle swarm optimization [J]. Reliability Engineering and System Safety, 2014,127:65-76.

[20] SHEIKHALISHAHI M, EBRAHIMIPOUR V, SHIRI H, et al. A hybrid GA-PSO approach for reliability optimization in redundancy allocation problem [J]. Int J Adv Manuf Technol, 2013,68:317-338.

[21] dos SANTOS COELHO L. An efficient particle swarm approach for mixed-integer programming in reliability-redundancy optimization applications [J]. Reliability Engineering and System Safety, 2009,94:830-837.

(编辑 沈玉英)

Reliability redundancy optimization allocation of integrated monitoring and control system of deep-sea drilling rig

WANG Hongyan1, XIAO Wensheng1,2, LIU Jian1, WANG Fengde1, HOU Chao1, CUI Junguo1

(1.CollegeofMechanicalandElectronicEngineeringinChinaUniversityofPetroleum,Qingdao266580,China;2.ResearchInstituteofPetroleumExplorationandDevelopment,PetroChina,Beijing100083,China)

The techniques of redundancy can be used to enhance the reliability of the integrated monitoring and control system of deep-sea drilling rig (DSDR-IMCS) ), which results in cost, weight and volume increasing. A mathematical model of reliability redundancy optimization allocation (RROA) was developed based on the analysis of DSDR-IMCS. A hybrid algorithm was proposed to solve the mathematical model, which combines particle swarm optimization(PSO) algorithm, genetic algorithm (GA) with simulated annealing (SA). Using the fast convergence rate of PSO and good global convergence of GA integrating SA, the new particles of PSO were modified. The numerical simulation results show that the proposed method can not only accelerate calculation speed, reduce the calculation intensity, improve the search efficiency, but also avoid the problem of reducing the capability of global search resulting from rapid convergence. This hybrid algorithm can generate better optimization results, so it can provide a reference for the analysis and design of DSDR-IMCS reliability optimization.

integrated monitoring and control system(IMCS); reliability; redundancy; optimization allocation; simulated annealing; PSO-GA method

2014-10-09

国家“863”高技术研究发展计划(2012AA09A203)

王鸿雁(1980-)，女，博士研究生，主要从事海洋石油钻采装备的研究。E-mail：wanghy0546@163.com。

1673-5005(2015)01-0128-08

10.3969/j.issn.1673-5005.2015.01.019

TE 52;TP 336

A

王鸿雁,肖文生,刘健，等. 深水钻机集成监控系统可靠性冗余优化[J].中国石油大学学报:自然科学版, 2015,39(1):128-135.

WANG Hongyan, XIAO Wensheng, LIU Jian,et al. Reliability redundancy optimization allocation of integrated monitoring and control system of deep-sea drilling rig[J]. Journal of China University of Petroleum (Edition of Natural Science), 2015,39(1):128-135.