一裂缝变缝宽形态对压裂井长期产能的影响

郭建春, 刘 恒, 曾凡辉

(1.西南石油大学油气藏地质及开发工程国家重点实验室,四川成都 610500;2.西南石油大学石油与天然气工程学院，四川成都 610500)

一裂缝变缝宽形态对压裂井长期产能的影响

郭建春1, 刘 恒2, 曾凡辉2

(1.西南石油大学油气藏地质及开发工程国家重点实验室,四川成都 610500;2.西南石油大学石油与天然气工程学院，四川成都 610500)

基于流体扩散理论和势叠加原理,采用半解析方法研究盒形封闭边界下垂直裂缝压裂井的油藏渗流和裂缝流动过程并建立相应数学模型,对压裂井的不稳定产能进行预测，并对裂缝非均匀流入剖面进行模拟。结果表明:生产初期,流入量集中于近井筒附近的裂缝,进入拟稳态阶段后流入量集中于裂缝趾部;裂缝沿缝长变窄的形态在生产初期不影响产能,由于流体流入裂缝的位置向裂缝趾部集中,裂缝趾部越窄,产量越低;拟稳态阶段时,等缝宽与变缝宽裂缝间的累积产量差距加大,产量差距主要集中于裂缝后1/3区域,该区域贡献了裂缝约一半的累积产量。加宽裂缝趾部缝宽能提高和保持压裂井在拟稳态阶段的产量,对压裂井的稳产、高产具有意义。

油藏; 流体扩散; 不稳定产能; 变缝宽; 流入剖面; 压裂井

半解析模型由于其计算参数较少但结果准确成为水力压裂裂缝产能研究的重要方法[1-2]。国内外学者利用半解析方法计算出裂缝拟稳态阶段的流入剖面[3-4],获得了均质化裂缝的不稳定产能[5-10]。以上研究都未将裂缝沿缝长缝宽变窄的实际形态纳入模型计算。有学者使用有限元法模拟了楔形裂缝的压裂井动态特征，但计算方法复杂耗时[11-12]。笔者考虑裂缝面上的非均匀流入与裂缝缝宽的实际形态,建立水力压裂井的不稳定产能模型,分析裂缝趾部缝宽对裂缝保持长期产能的重要作用。

1 数学模型的建立

1.1 油藏渗流模型

盒形封闭边界垂直裂缝井物理模型如图1所示。

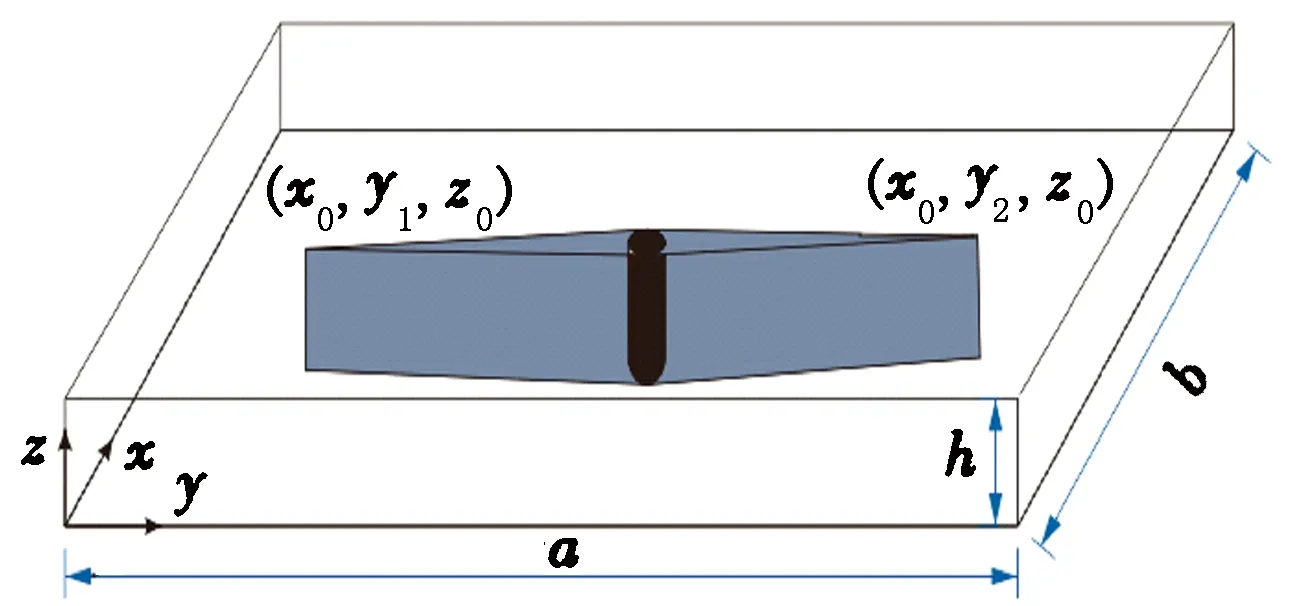
图1 盒形封闭边界垂直裂缝井物理模型Fig.1 Vertical fractured well physical model in box-type closed boundary

上顶下底矩形封闭非均质油藏中心一口直井,压出对称双翼裂缝完全穿透产层,裂缝采用由跟部到趾部缝宽变窄的楔形模型,位置从(x0,y1,z0)到(x0,y2,z0),且与y轴平行(图1)。流体在油藏和裂缝内的流动为单相流,流动过程为先沿裂缝壁面不均匀流入裂缝,再经裂缝流入井筒。油藏的孔隙度φ和3个方向上渗透率kx、ky、kz为常数。流体单向微可压缩,初始时刻t=0时,整个油藏的压力为常数。

油藏的初始时刻各边界并无流体流动,油井开始生产时沿裂缝壁面某点流入流体会对整个油藏产生瞬时压降。假设在单位时间t0到t内,裂缝上某点(x0,y0,z0)流体以q(t)的速度流入,则其对裂缝上任意点(x,y,z)产生的压降[13]为

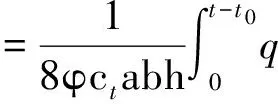
S(x,τ)S(y,τ)S(z,τ)dτ.

(1)

其中

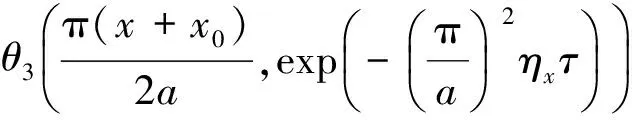
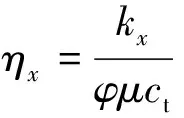
θ3(πx,exp(-2π2τ))=

式中,pini为油藏原始地层压力,MPa;S(x,τ)S(y,τ)S(z,τ)为点(x0,y0,z0)生产时对点(x,y,z)产生的点汇解;θ3为第三类椭圆函数;ct为储层综合压缩系数,MPa-1;φ为孔隙度;a、b和h分别为盒形储层的长、宽和高,m;ηx为x方向的导压系数,10-3m2。

假设裂缝完全穿透油藏产层,图1的三维模型可简化为图2的二维平面模型。为描述流量沿裂缝的非均匀分布,将每个单翼裂缝分为n段(图2),每段微元可视为一个点汇。式(1)适合每个点汇,故油井生产时每个点汇都有相应流量qj流入,根据势叠加原理,裂缝上任意点(x,y,z)在t时刻的总压降为

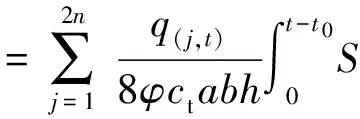
S(z,τ)dτ.

(2)

式中,n为裂缝单翼微元段数目;q(j,t)为第j个点汇在t时刻的产量,m3。

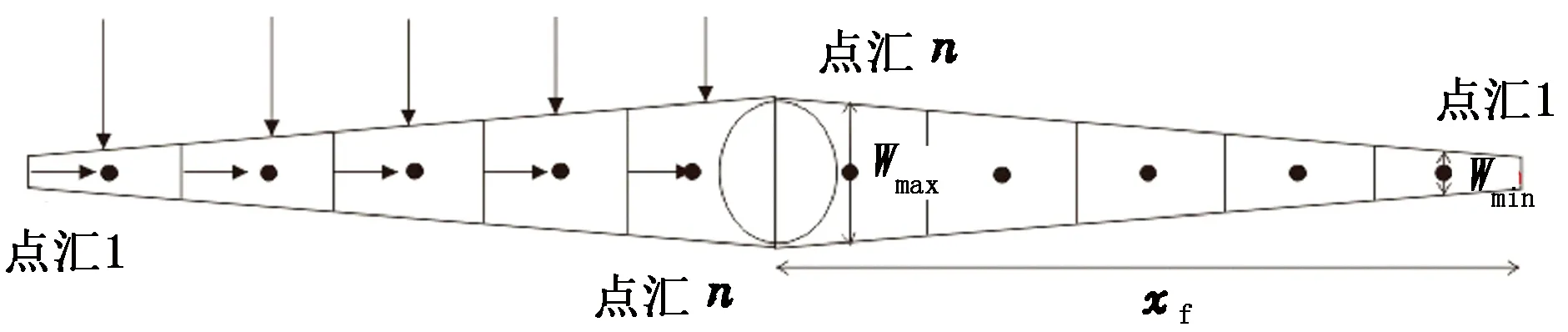
图2 裂缝流动及空间离散化示意图Fig.2 Flow in fractures and spatial discrete schematic

1.2 裂缝渗流模型

依据裂缝缝宽由跟部到趾部逐渐变窄的事实,将裂缝处理为等腰梯形。按图2所示,裂缝上任意点(xk,yk)的缝宽可表示为

Wk=Wmin+(2k-1)(Wmax-Wmin)/(2n).

(3)

式中,Wmin为裂缝趾部的缝宽,mm;Wmax为裂缝跟部的缝宽,mm。

假设流体流入裂缝以后向井筒的流动为线性流动，而井筒为无限导流，则裂缝内任意点(xk,yk)到井筒的压降为

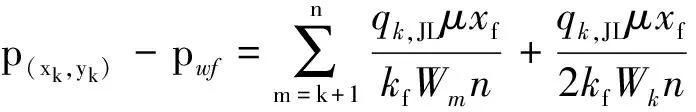
(4)

其中

式中,p(xk,yk)为裂缝内点(xk,yk)处的压力,MPa;kf为裂缝渗透率,10-3μm2;qk,JL为裂缝内点(xk,yk)处的截流量,m3。

1.3 耦合流动模型

油藏流体在储层内流动与在裂缝内流动对裂缝壁面造成的压力相等,根据式(2)与式(4)建立油藏-裂缝-井筒连续性方程为

(5)

式(5)通过空间离散实现了对裂缝流入剖面的不均匀计算。若将时间τ看成未知数,则方程可表示为

Δp=qF(τ) .

(6)

为计算裂缝流入剖面随时间的变化,可利用时间叠加原理计算裂缝上任意点汇在任意时刻的产量[14],表达式为

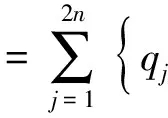
(7)

1.4 求解方法

将2n个油藏-裂缝-井筒耦合方程构成的线性方程组转化为矩阵形式,可表示为

Aq=B.

(8)

其中

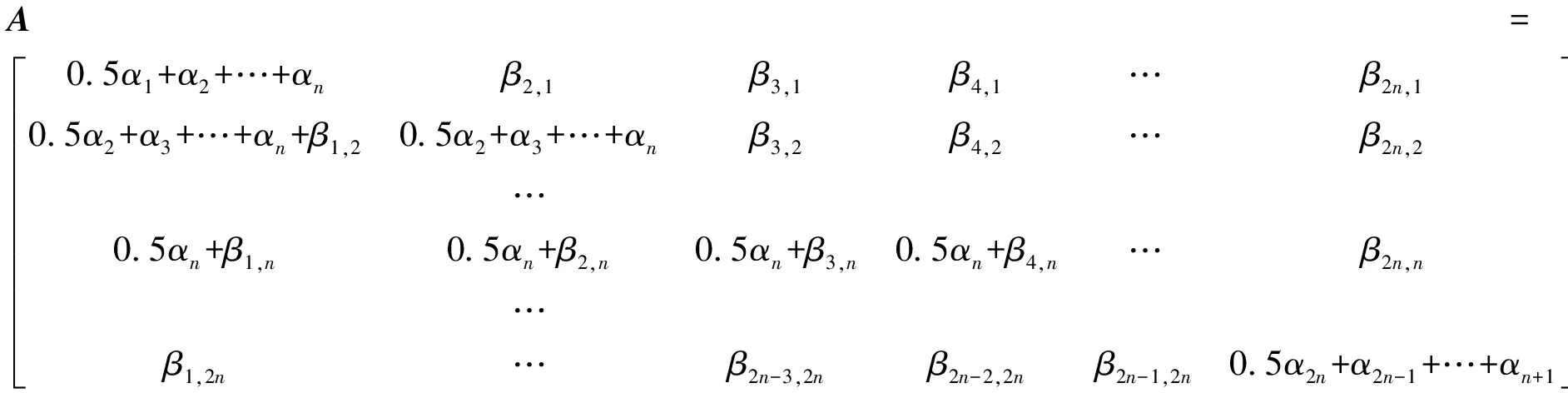
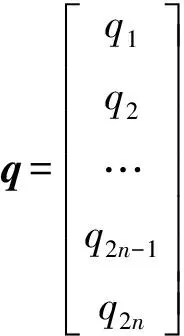
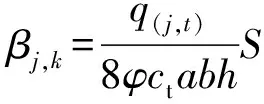
式中,αj为裂缝第j个单位缝长裂缝内压降系数,MPa/m3;βj,k为裂缝上第j个点汇对第k个点汇的压降系数,MPa/m3。

在计算任意时刻(nΔt)的q时,将之前时刻的q和F带入式(7)即可构造出新的线性方程组。由于裂缝内为一维线性流动,式(7)始终为线性方程组,通过高斯赛德尔迭代即可求解。

2 裂缝趾部宽度对产能的影响

为计算压裂井的生产动态,选取A油田某压裂油井的基础参数:油藏的初始压力为16.7MPa,井底压力为8.6MPa,油藏厚度为9.8m,地层渗透率为1.7×10-3μm2,地层孔隙度为0.16,井筒半径为0.12m,体积系数为1.1,原油黏度为8.5mPa·s,压缩系数为0.34kPa-1,裂缝起点宽度为6.0mm,裂缝终点宽度为2.5mm,裂缝单翼长度为100m,裂缝渗透率为90μm2。油藏泄油面积500m×200m,压裂后在垂直井段上形成一条对称双翼裂缝,模拟时间为500d,裂缝单翼均分为50等份。

2.1 模型验证

分别采用模型1[15]、模型2[16](模型2计算单条裂缝时即为垂直压裂井产能模型)及本文中方法进行产能计算,计算结果见表1。

表1 压裂井产量计算结果

可以看出,使用本文中方法计算的产能最接近实际产量(25.5 m3/d),说明建立的产能模型准确性较高。

2.2 缝内流量分布与时间关系

考察裂缝内流量随时间的变化情况,结果如图3所示。

在生产初期,距离井筒10 m处的缝内流量仅占总流量的29%,说明此时71%的流体是通过井筒附近10 m的裂缝壁面流入。生产20 d时,缝内流量从趾部到跟部呈线性增加,说明流体沿裂缝均匀流入。生产100 d时,距离井筒75 m处的缝内流量达到总流量的52%,说明进入拟稳态生产条件后大部分流量通过裂缝远端(特别是裂缝趾部)进入裂缝。随着时间的增加,沿裂缝壁面的入流量由裂缝跟部向裂缝趾部集中,裂缝由跟部向趾部缝宽的变化对压裂井产量产生重要影响。

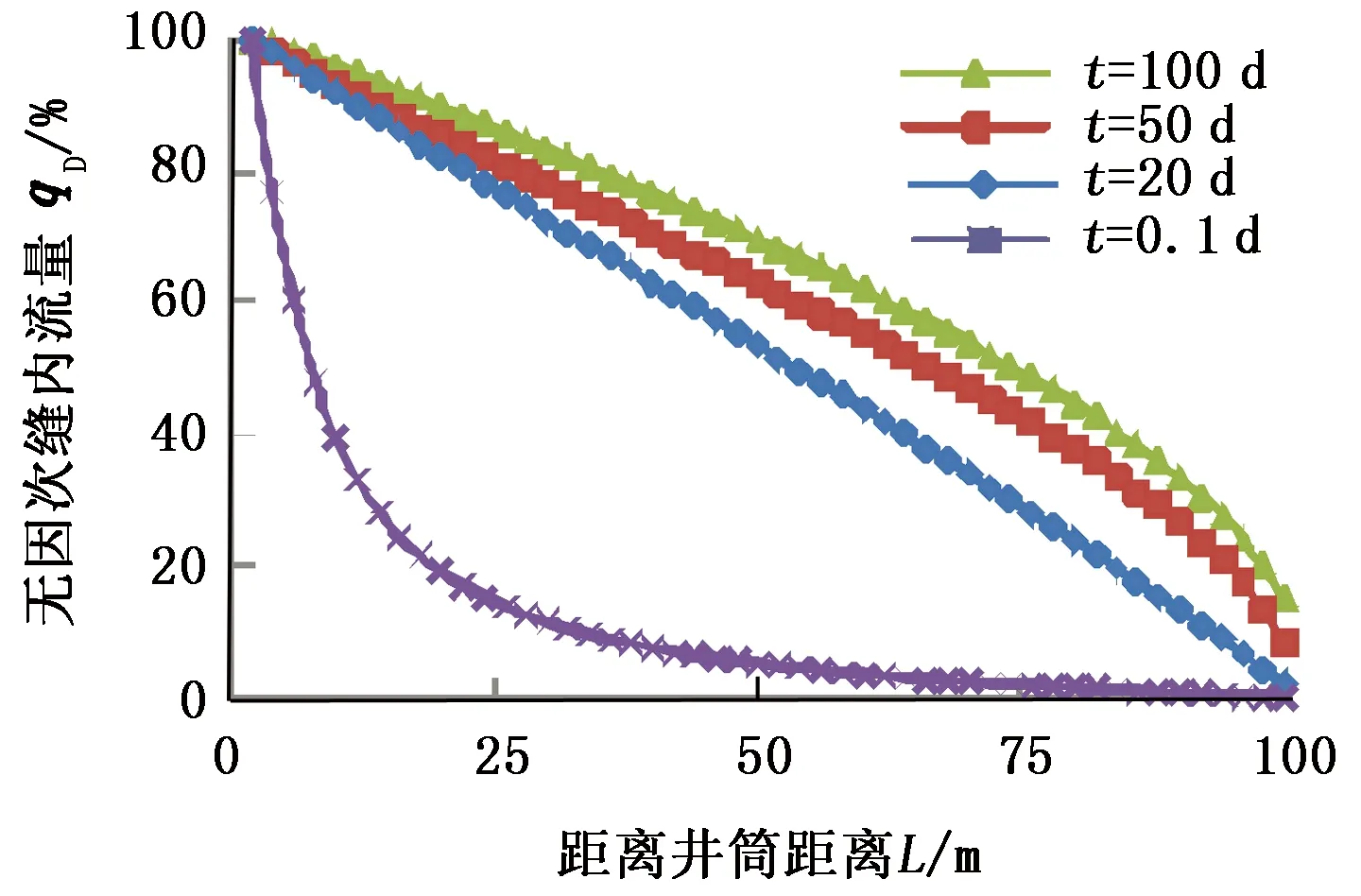
图3 缝内流量分布与时间的关系Fig.3 Relationship between flux distribution and time

2.3 裂缝流入剖面与裂缝形态关系

在生产100 d时，裂缝跟部到趾部裂缝变窄的程度对裂缝流入剖面的影响如图4所示。

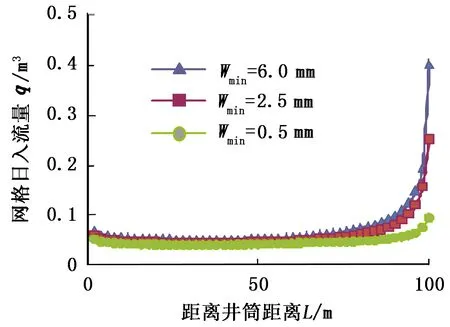
图4 裂缝流入剖面与裂缝形态关系Fig.4 Relationship between inflow velocity profile and fracture morphologies

由图4可见,在裂缝跟部缝宽不变的情况下,由于趾部缝宽变窄,导流能力下降导致流体进入裂缝趾部阻力增大,2.5 mm 缝宽的裂缝日产量要比6 mm 缝宽条件下小0.5 m3,0.5 mm缝宽的裂缝要比6 mm 缝宽条件下小0.8 m3。

2.4 裂缝累积产量与裂缝缝宽关系

沿裂缝跟部到趾部缝宽变窄的程度对压裂井累积产量的影响如图5所示。

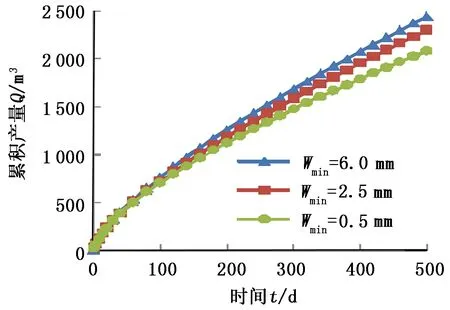
图5 楔形裂缝与等缝宽裂缝累积产量对比Fig.5 Cumulative production comparison of wedge fracture and fracture with same width

由图5可知,压裂井进入拟稳态阶段后楔形裂缝的累积产量会逐渐小于等缝宽裂缝产量,趾部缝宽为2.5 mm的裂缝比等缝宽裂缝产量减少6.3%,趾部缝宽为0.5 mm的裂缝比等缝宽裂缝产量减少17.3%。

为精确分析裂缝不同位置对累积产量的贡献程度,将100 m的裂缝分为裂缝前段(0～34 m)、裂缝中段(34～67 m)和裂缝尾段(67～100 m)3部分,每个部分在生产500 d时的累积产量如图6所示。

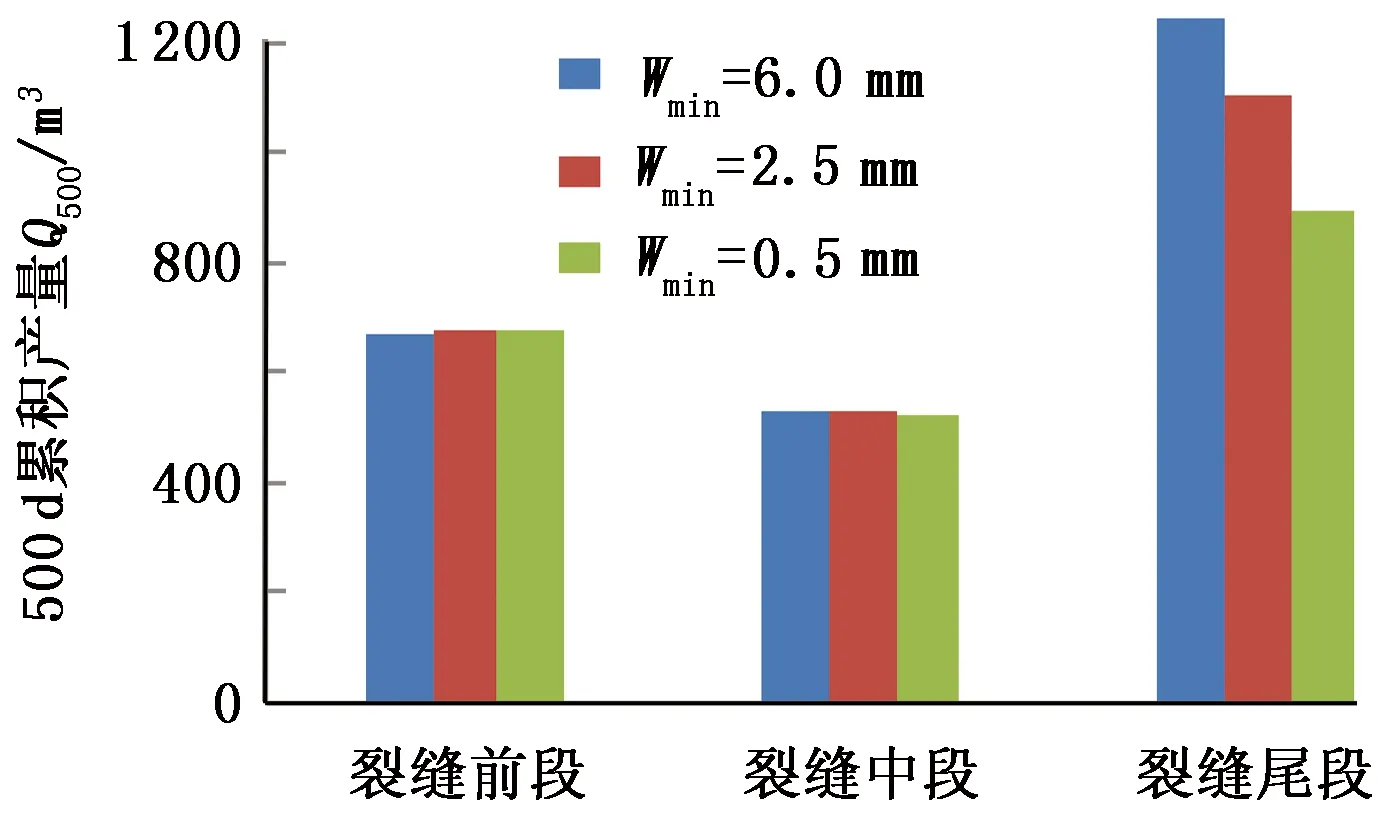
图6 裂缝各部分累积产量Fig.6 Cumulative production of fractures three segments

由图6可知,裂缝尾段的累积产量接近于总量的一半,等缝宽与楔形裂缝累积产量的差距也主要存在于该区域。

在压裂设计和实际生产中若采用适当工艺(如采用低密度支撑剂、端部脱砂工艺等)提高和保持裂缝趾部缝宽,裂缝趾部的产量将在拟稳态阶段提高,进而促进压裂井的长期稳产。

3 结 论

(1)基于流体扩散理论和势叠加原理,通过空间离散和时间叠加实现了封闭盒形油藏中有限导流能力裂缝的不均匀流入剖面计算和压裂井不稳定动态产能预测。该计算模型可推广到多段压裂水平井的产能计算。

(2)随时间的增加,裂缝流入剖面由井筒附近向裂缝趾部集中;裂缝沿缝长变窄的形态在生产初期并不影响产能,但随着流体流入裂缝位置向裂缝趾部的集中,窄小的裂缝趾部成为限制拟稳态条件下产量的因素,与理想的等缝宽裂缝相比会损失产能。裂缝的累积产量一半集中于裂缝近趾部1/3区域,加宽裂缝趾部缝宽能进一步提高压裂井在拟稳态阶段的产量。

[1] ROMERO D J, VALKO P P, ECONOMIDES M J. Optimization of the productivity index and the fracture geometry of a stimulated well with fracture face and choke skins[J]. SPE Production & Facilities, 2003,18(1):57-64.

[2] LIU H, ZENG F, YAO S. A semi-analytical model for hydraulically fractured wells with stress-sensitive conductivities[R]. SPE 167230, 2013.

[3] 汪志明, 齐振林, 魏建光, 等. 裂缝参数对压裂水平井入流动态的影响[J]. 中国石油大学学报:自然科学版, 2010,34(1):73-78. WANG Zhiming, QI Zhenlin, WEI Jianguang, et al. Influence of fracture parameters on inflow performance of fractured horizontal wells [J]. Journal of China University of Petroleum(Edition of Natural Science), 2010,34(1):73-78.

[4] 汪志明, 金辉, 魏建光. 压裂水平井裂缝变质量入流与油藏渗流耦合模型研究[J]. 水动力学研究与进展:A辑, 2009,24(2):172-179. WANG Zhiming, JIN Hui, WEI Jianguang. Interpretation of the coupling model between fracture variable mass flow and reservoir flow for fractured horizontal wells[J]. Chinese Journal of Hydrodynamics(ser A), 2009,24(2):172-179.

[5] SHAHRAM A, VALKP P. Using distributed volumetric sources to predict production from multiple fractured horizontal wells under non-Darcy-flow conditions[R]. SPE 120110, 2010.

[6] JIA Jinglin, DING Zhu. Modeling well performance for fractured horizontal gas wells [R]. SPE 130794, 2010.

[7] 徐严波, 齐桃, 杨凤波. 压裂后水平井产能预测新模型[J]. 石油学报, 2006,27(1):89-96. XU Yanbo, QI Tao, YANG Fengbo. New model for productivity test of horizontal well after hydraulic fracturing[J]. Acta Petrolei Sinica, 2006,27(1):89-96.

[8] 廉培庆, 程林松, 何理鹏. 气藏压裂水平井非稳态流动分析[J]. 计算力学学报, 2011,28(4):579-583. LIAN Peiqing, CHENG Linsong, HE Lipeng. Analysis of transient flowing model for fractured horizontal well in gas reservoir [J]. Chinese Journal of Computational Mechanics, 2011,28(4):579-583.

[9] 孙海, 姚军, 廉培庆, 等. 考虑基岩向井筒供液的压裂水平井非稳态模型[J]. 石油学报, 2012,33(1):117-122. SUN Hai, YAO Jun, LIAN Peiqing, et al. A transient reservoir/wellbore coupling model for fractured horizontal wells with consideration of fluid inflow from base rocks into wellbores[J]. Acta Petrolei Sinica, 2012,33(1):117-122.

[10] 郝明强, 胡永乐, 李凡华. 特低渗透油藏压裂水平井产量递减规律[J]. 石油学报, 2012,33(2):269-273. HAO Mingqiang, HU Yongle, LI Fanhua. Production decline laws of fractured horizontal wells in ultra-low permeability reservoirs[J]. Acta Petrolei Sinica, 2012,33(2):269-273.

[11] 刘振宇, 郑宪宝, 张应安. 基于有限元法的人工压裂井的产能动态分析[J]. 大庆石油学院学报, 2006,30(2):30-34. LIU Zhengyu, ZHENG Xianbao, ZHANG Yingan. Production performance research of fracturing well with finite element method[J]. Journal of Daqing Petroleum Institute, 2006,30(2):30-34.

[12] 蒋廷学, 郎兆新, 单文文, 等. 低渗透油藏压裂井动态预测的有限元方法[J]. 石油学报, 2002,23(5):53-58. JIANG Tingxue, LANG Zhaoxin, SHAN Wenwen, et al. Finite element method for postfracturing production performance of wells in low-permeability reservoir[J]. Acta Petrolei Sinica, 2002,23(5):53-58.

[13] PHILLIP G J, BUSSWELL G, BANERJEE R. Semi-analytical solution for multiple layer reservoir problems with multiple vertical, horizontal, deviated and fractured wells [R]. IPTC 11718, 2007.

[14] VISWANATHA R P. Modeling of horizontal wells with pressure drop in the well [D]. Stanford: Department of Petroleum Engineering of Stanford University, 1997.

[15] PRATS M, HAZEBROEK P, STRICKLER W R. Effect of vertical fractures on reservoir behavior: compressible fluid case [J]. SPE Journal, 1962,2(2):94-97.

[16] 曾凡辉, 郭建春, 赵金洲. 影响压裂水平井产能的因素分析[J]. 石油勘探与开发,2007,34(4):474-477. ZENG Fanhui, GUO Jianchun, ZHAO Jinzhou. Factors affecting production capacity of fractured horizontal wells [J]. Petroleum Exploration and Development, 2007,34(4):474-477.

(编辑 李志芬)

Influence of varying fracture width on fractured wells long-term productivity

GUO Jianchun1, LIU Heng2, ZENG Fanhui2

(1.StateKeyLaboratoryofOilandGasReservoirGeologyandExploitation,SouthwestPetroleumUniversity,Chengdu610500,China;2.SchoolofOil&NaturalGasEngineeringofSouthwestPetroleumUniversity,Chengdu610500,China)

The flow behavior in reservoir matrix and fractures for oil production through a fractured vertical well was investigated based on fluid diffusion theory and potential superposition principles. A semi-analytical model was established, which can be used to predict wells transient productivity considering uneven inflow profiles along the fracture. The results show that the early production is mainly from the panels close to the wellbore, and then from the far end of the fracture in later time. The wedge-shape of the fracture has little effect on the initial productivity, but when the fluid inflow toward the end of the fracture, the narrower the fracture tip, the lower the production is observed. At a pseudo-steady state, the difference of cumulative production between a constant width fracture and that of wedge-shaped can be significantly large, which mainly appears at the 1/3 end part of the fracture, but accounts for a half of the total production. Widening the width of the fracture tip can improve the productivity of fractured wells at pseudo-steady state.

reservoir; fluid diffusion; transient productivity; varying fracture width; inflow profile; fractured well

2014-06-25

国家自然科学基金项目(51074138);四川省青年科技创新研究团队专项(2011JTD0018)

郭建春(1970-)，男，教授，博士，博士生导师，主要从事油气藏开采和增产技术研究。E-mail:guojianchun@163.vip.com。

1673-5005(2015)01-0111-05

10.3969/j.issn.1673-5005.2015.01.016

TE 355.6

A

郭建春,刘恒,曾凡辉. 裂缝变缝宽形态对压裂井长期产能的影响[J]. 中国石油大学学报:自然科学版,2015,39(1):111-115.

GUO Jianchun, LIU Heng, ZENG Fanhui. Influence of varying fracture width on fractured wells long-term productivity[J]. Journal of China University of Petroleum(Edition of Natural Science),2015,39(1):111-115.