基于改进的小波核主元分析故障检测

张端金，汪爱娟

(郑州大学 信息工程学院，河南 郑州 450001)

基于改进的小波核主元分析故障检测

张端金，汪爱娟

(郑州大学 信息工程学院，河南 郑州 450001)

研究了基于核主元分析的非线性系统故障检测问题.提出了一种改进的小波核主元分析的故障检测方法.该方法首先对数据进行小波去噪预处理，然后再利用小波核函数，将非线性的输入空间转换到线性特征空间.在特征空间使用主元分析，结合SPE统计量和T2统计量对非线性系统进行故障检测.仿真结果表明：该方法能够提高故障检测性能.

核主元分析；小波核函数；小波去噪；故障检测

0 引言

随着现代工业和科学技术的飞速发展，设备的结构变得复杂化.系统的安全性和可靠性对人类社会产生巨大影响.因而，对这类系统进行故障检测设计具有重大的现实意义.

近年来，多变量过程控制技术得到了很大的发展，取得很多成果.Chan等[1]提出了基于特征值分解的改进PCA故障检测方法，马贺贺等[2]利用高阶统计量来获取过程信息，提出了一种新的统计量核主元分析方法，故障检测.郭珂[3]提出了一种小波核函数用于故障检测，但是没有对采集数据进行预处理.陈亮等[4]采用多项式核函数对非线性系统故障进行检测，对数据预先进行了小波去噪处理，提高了故障检测性能.倪国文[5]提出了PCA本身就是一种去噪方法，自身实现了数据预处理，达到了很好的检测效果.

综上，文献中还没有用到小波核函数和小波去噪结合起来进行故障检测的方法.基于此，笔者提出了一种新的非线性故障检测方法.利用小波核函数和小波去噪相结合的方法进行故障检测.并通过算例仿真，验证了该方法的有效性.

1 小波分析

采集到的数据包含噪声，直接利用这些受噪声干扰的数据进行故障检测，必然会影响故障检测的准确性.因此，在进行故障检测之前对数据进行去噪处理是必要的.

小波变换是时间和频率的局部变换，因而能有效地从信号中提取信息.通过伸缩和平移运算可对函数或信号进行多尺度的细化分析，解决了傅里叶变换不能解决的许多困难问题.

2 基于小波核主元分析故障检测

小波核主元分析方法在故障检测中能够很好地提取系统中的非线性特征信息，减少重要信息的丢失.因此，该方法可以提高故障检测的准确率，大大减少误报和漏报率，具有很好的非线性故障检测能力.

2.1 小波核主元分析

由Scholkopf[6]提出的核主元分析能够弥补主元分析在处理非线性系统方面的缺陷，很好地捕捉非线性系统的特征信息.

已知采样数据Xn×m=[x1,x2,…,xn](xi∈Rm,i=1,2,…,n)，n为采样点数，m为变量个数.将采样数据通过非线性变换φ，影射到高维特空间征，再利用主元分析法，结合SPE统计量和T2统计量进行故障检测.

在特征空间中，假设φ(xi),i=1,2,…,n已经过中心化处理，采样协方差矩阵可以表示为

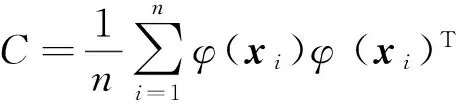
(1)

通过确定C的特征向量ν就可以获得特征空间中的主元.

λν=Cν.

(2)

在λ≠0的条件下，ν的所有解都可以由φ(xi),i=1,2,…,n表示，即

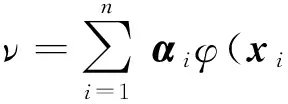
(3)

因此，式(2)可以表示为

λ<φ(xk),ν>=<φ(xk),Cν>.

(4)

由式(3)和式(4)得

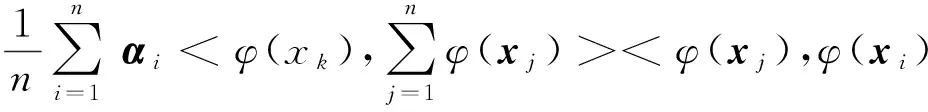
(5)

小波函数如下所示：

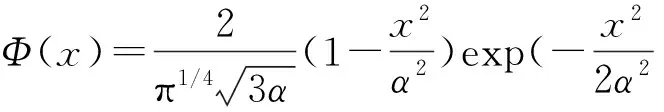
(6)

把上式看做一个母小波，如果x,x′∈Rn，那么小波核函数为

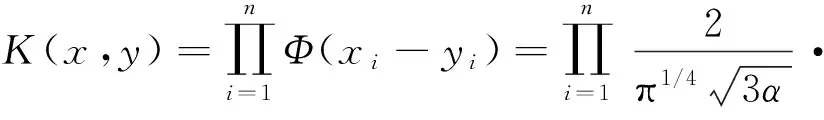
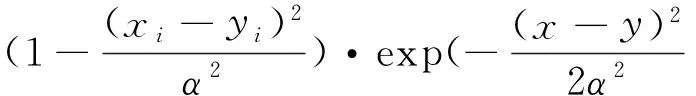
(7)

具体的证明过程详见文献[2].

定义一个小波核矩阵K，如下所示：

[K]ij=K(xi,xj)=<φ(xi),φ(xj)>.

(8)

式中：K(xi,xj)是在特征空间中利用核函数计算两个向量的内积.

把式(5)代入式(8)中，可以得到

nλα=Kα.

(9)

其中，α=[α1,α2,…,αn]T，式(9)的求解问题和在特征空间中进行主元分析是等价的.

令λ(λ1≥λ2≥…λn)为K的特征值，那么α=[α1,α2,…,αn]T为对应的特征向量.对特征向量ν进行归一化

<νk,νk>=1.

(10)

由式(3)可得

λk<αk,αk>=1.

(11)

那么任何一个样本向量x在特征空间中的第k个主元计算为

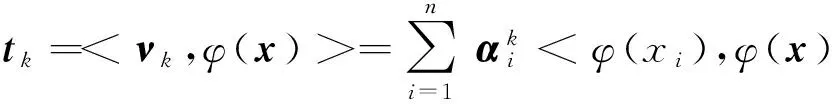
(12)

在特征空间中进行主元分析之前，先对矩阵K进行标准化处理，因为假设特征空间中数据的均值是零，而实际运算用到的是核矩阵K，所以要对它进行如下标准化处理.具体推导过程详见文献[7].

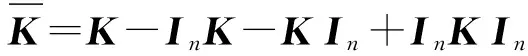
(13)

2.2 故障检测

T2统计量的定义为

T2=[t1,t2,t3…tk]Λ-1[t1,t2,t3…tk]T.

(14)

如果样本的均值和协方差分别与建模样本的均值和协方差相等，则T2统计量服从自由度为K的χ2分布.如果给定显著性水平α，那么T2统计量的控制限由下式计算

中国共产党领导全国各族人民经过长期斗争和实践中形成的红色文化，为做好新时期高校党建工作与思政工作提供了最好的营养剂。大学是文化传承与创新的重要阵地。在新的历史条件下，传承和创新红色文化成为高校文化育人的重要着力点，在树立大学生正确的世界观、人生观和价值观过程中至关重要，为培养合格的社会主义建设者和可靠的接班人提供强大驱动力。

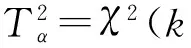
(15)

如果样本的协方差未知，而是通过建模样本的协方差矩阵来估计时，T2统计量服从自由度为k和n-k的F分布，n是样本点数.T2统计量的控制限由下式计算.

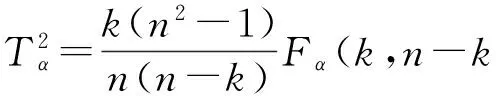
(16)

在正常情况下，T2统计量的值应处于该控制限之内，出现故障时，统计量会超出控制限.

SPE统计量的定义为

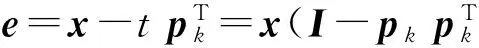
(17)

SPE=eeT.

(18)

给定显著性水平为α，计算SPE统计量的控制限为

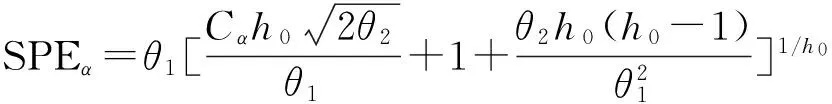
(19)

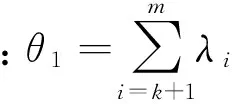
对新的采样数据进行故障检测时，建立检测统计量指标进行假设检验，通过计算检测统计量是否超过控制限，来判断故障是否发生.

改进的算法步骤如下.

(1)采样得到正常无故障样本X，并标准化.然后用db5小波对X中的每一列数据去噪；

(2)选择小波核函数做非线性映射，计算核矩阵K∈Rn×n，Kij=K(xi,xj)=<φ(xi),φ(xj)>，n为采样点数；

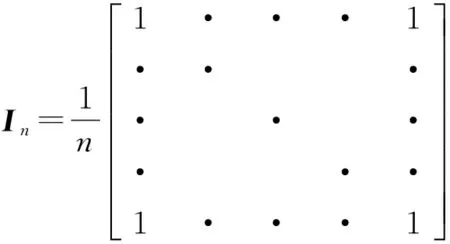
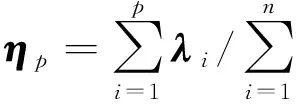
(6)计算T2和SPE控制限；

以上步骤是正常无故障数据的建模模型.

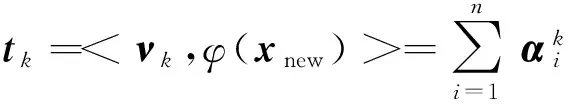
(8)计算新的统计量，检测是否超出控制限.

3 仿真研究

以如下典型的非线性系统[8]为研究对象.

(20)

其中，e1，e2和e3为服从均值为零，方差为0.01的正态独立噪声变量，t∈[0.01,2].取400个无故障数据采样点，建立KPCA故障检测模型，然后取200个有故障数据采样点，在第160个采样点引入均值为0.5的偏差故障.本仿真系统采用小波核函数，kw(x,x′)=(1-(‖x-x′‖2/α))exp(-(‖x-x′‖2/α))，α=45.所得结果如图1和图2所示，结合SPE和T2统计量，横线代表99%的控制限，超出红线为故障数据点，横线以下为正常数据点.据此，能判断出系统是否发生故障.

在图1和图2中，T2统计量的仿真图形变化趋势基本一致，在1～159个采样点之间均没有超出控制限制，代表采样信号在主元空间没有发生偏移，160～200个采样点之间超出控制限，代表采样信号在主元空间发生了偏移，出现了故障.图1中，SPE统计量的仿真图，1～159是正常数据点，但超过99%控制限的数据点有12个，误报率为7.55%.图2中，SPE统计量的仿真图，1～159是正常数据点，但超过99%控制限的数据点有2个，误报率为1.26%.图1采用的是marr小波核，

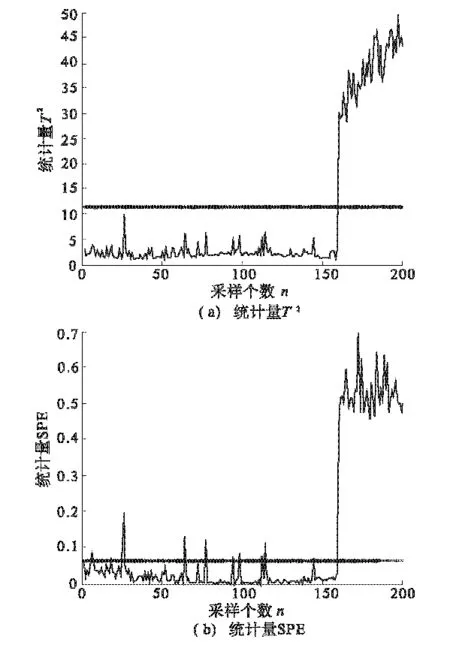
图1 小波核主元分析检测结果Fig.1 Detection results of wavelet kernel principal analysis

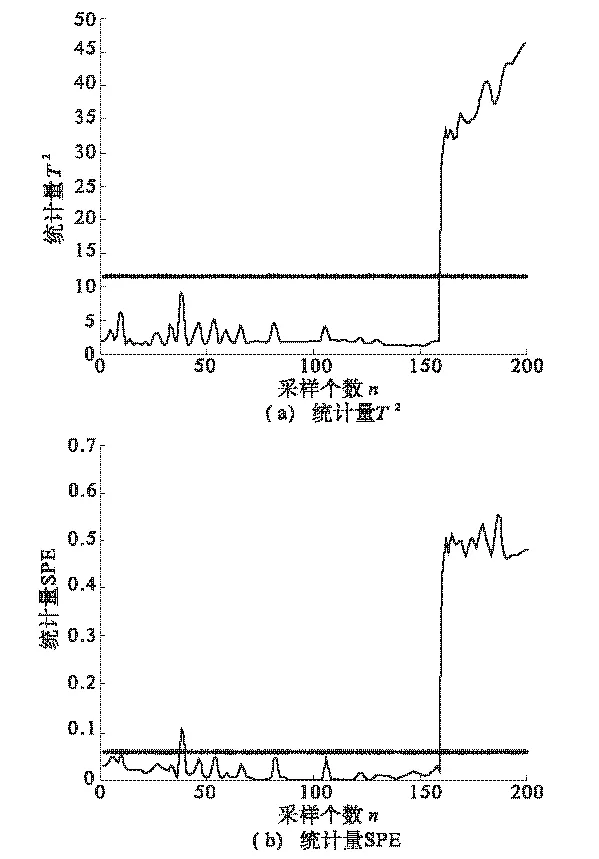
图2 改进的小波核主元分析检测结果Fig.2 Detection faults of the improved wavelet kernel principal analysis

没有进行去噪处理.图2采用的是marr小波核，小波去噪用的是db5小波.核参数取45.图1比图2的误报率高，原因是采集到的数据包含噪声，直接利用这些受噪声干扰的数据进行故障检测，必然会影响故障检测的准确性.由此可见，采用小波去噪对数据进行处理，减小了噪声对故障检测的影响，降低误报率，提高检测性能.

4 结论

笔者给出了小波核函数和小波去噪相结合的故障检测方法.首先，对采样数据利用小波去噪进行预处理，提高了建立模型的准确性.然后利用小波核主元分析进行故障检测，大大提高了故障检测率.通过算例仿真，验证了该方法的有效性.

[1] CHAN S C, WU H C, TSUI K M. Robust recursive eigendecomosition and subspace-based algorithms with application to fault detection in wireless sensor networks[J]. IEEE Trans on Instrumentation and Measurement, 2012, 61(6): 1703-1718.

[2] MA He-he, HU Yi, SHI Hong-bo. Statistics kernel principal component analysis for nonlinear process fault detection[C]//Proceedings of the 9th World Congress on Intelligent Control and Automation. Taibei, 2011: 431-436.

[3] GUO Ke, SAN Ye, ZHU Yi. Nonlinear process monitoring using wavelet kernel principal component analysis[C]//Proceedings of International Conference on Systems and Informatics. Yantai, 2012: 432-438.

[4] CHEN Liang, YU Yang，LUO Jie, et al. An improved fault detection algorithm based on wavelet analysis and kernel principal component analysis[C]//Proceedings of Chinese Control and Decision Conference. Xuzhou, 2010: 1723-1726.

[5] 倪国文,刘爱伦. 基于核主元分析的非线性故障检测研究[J]. 仪器仪表学报, 2009,30(6): 443-447.

[6] SCHOLKOPF3 B, SMOLA A, MULLER K. Nonlinear component analysis as a kernel eigenvalue problem [J]. Neural Computation, 1988, 10(5): 1299-1319.

[7] NOWICKI A, GROCHOWSKI M, DUZINKIEWICZ K. Data-driven models for fault detection using kernel PCA: A water distribution system case study [J]. International Journal of Applied Mathematics and Computer Science, 2012, 22(4): 939-949.

[8] LEE J M, YOO C K, CHOI S W, et al. Nonlinear process monitoring using kernel principal component analysis[J]. Chemical Engineering Science, 2004, 59(1):223-234.

Fault Detection Based on Improved Wavelet Kernel Principal Component Analysis

ZHANG Duan-jin, WANG Ai-juan

(School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China)

The problem of fault detection for a class of nonlinear systems based on kernel principal component analysis is studied. The improved wavelet kernel principal component analysis is proposed. Firstly, the proposed method is applied to denose the data. Then, the preprocessed data is transformed by wavelet kernel function to map the nonlinear input space into linear characterization space. In the feature space, principal component analysis is applied to detect faults for nonlinear system, in combination with SPE statistic and T2statistic. Simulation results show that the method can improve the fault detection performance.

kernel principal component analysis； wavelet kernel function； wavelet denoising； fault detection

2014-08-07；

2014-11-10

国家自然科学基金资助项目(61471323)；河南省教育厅科学技术研究重点项目(14A120004)

张端金(1966-)，男，湖北荆州人，郑州大学教授，博士，研究方向为故障检测与估计，E-mail:djzhang@zzu.edu.cn.

1671-6833(2015)01-0097-04

TP273

A

10.3969/j.issn.1671-6833.2015.01.023