基于状态空间模型的神经元动态相关性研究

师 黎， 许昆峰， 牛晓可

(郑州大学 电气工程学院， 河南 郑州 450001)

基于状态空间模型的神经元动态相关性研究

师 黎， 许昆峰， 牛晓可

(郑州大学 电气工程学院， 河南 郑州 450001)

神经元间相关性的研究是深入理解神经元集群信息传递与编码机理的基础.首先，采用状态空间对数线性模型初步估计神经元间的动态相关性，针对输入数据特征对模型估计值置信区间的影响，提出了通过筛选数据优化置信区间来提高模型估计精度.然后，通过提取动态相关性的特征，分析神经元间相关性在不同朝向光栅刺激下的动态特性，进而研究了神经元间同步作用对视觉刺激信息的编码作用.最后，在麻醉的Long Evens(LE)大鼠初级视觉皮层上进行了实验验证.结果表明：采用剔除发放率偏小的序列的数据筛选方案能够有效地提高模型估计值的精度；神经元间的锋电位同步作用对朝向光栅刺激信息具有一定的编码作用.

状态空间对数线性模型； 动态相关性； 信息编码； 同步作用

0 引言

视觉是哺乳动物接收外界信息的主要途径，初级视觉皮层(Primary Visual Cortex,V1区)是大脑皮层中主要负责视觉信息处理的部分[1].大脑的信息处理是通过神经元在网络层次的动态相互作用实现的[2].神经元相关性的动态变化是神经元网络信息传递的基础[3].因此，神经元动态相关性的研究是神经科学领域的关键问题之一，对于揭示动物视觉系统信息编码机制具有重要意义[4-6].

对于神经元相关性的研究主要分两类:一类是侧重于衡量神经元间相关性的总体水平，另一类则侧重于估计相关性的动态变化过程.2006年，J.M.Samons等[7]等采用互相关图法研究了猫初级视觉皮层神经元间的相关性，该方法通过互相关函数的峰值大小来反映神经元间相关性的强弱.2007年，M.Fernando等[8]采集了麻醉猕猴V1区神经元对在不同方向正弦光栅刺激时的响应，采用移位预测改进互相关图法获取了神经元之间的相关性，该方法能够获取由刺激引发的相关性.以上研究所采用的方法仅侧重于计算神经元间的相关性强度，忽略了神经元间相关性的动态变化趋势.2012年，J.L.Reed等[9]采用联合刺激后时间直方图法，研究了麻醉猴子初级躯体感觉皮层神经元间相关性强度与手指刺激点间距之间的关系，该方法能够获取单次实验下相关性的动态变化，但多次实验得到结果的重复性较差.2012年，H.Shimazaki等[10]将状态空间对数线性模型应用于猴子运动皮层神经元间的动态相关性研究，作者针对运动皮层的神经元响应信号,采用Bayes统计方法估计模型输出值及其置信区间，没有对输入数据特征对模型置信区间的影响进行研究.

因此，针对上述问题，笔者分析了神经元锋电位数据特征对动态相关性模型输出置信区间的影响，提出了提高模型估计值精确度的方法,进而研究了朝向光栅刺激下神经元间动态相关性与信息编码的关系.

1 材料与方法

1.1 材料

实验对象为LE大鼠，体重在200～300 g之间，眼睛无异常.使用乌拉坦(20%，0.6 mL/100 g)对大鼠进行麻醉，然后，根据大鼠脑组织谱图，进行开颅手术，将铂铱合金材质的2×8 MicroProbe电极阵列植入V1区，深度约为900 mm.

刺激图为具有不同朝向的全屏正弦调制光栅，如图1所示.

图1 具有不同朝向的漂移光栅Fig.1 Drifting gratings with different orientations

在一组刺激实验中，每间隔1s随机转换一个朝向，每个朝向出现40次.经论证与试验，视觉刺激显示器距离大鼠眼睛的最佳距离为20 cm.

实验数据的采集用Black Microsystems公司的Cerebus多通道神经信号采集系统，共16个通道.在本研究中，采用主元分析和改进K均值相结合的锋电位分类方法[12].

1.2 方法

首先，采用状态空间对数线性模型估计神经元对在刺激下的动态相关性，初步确定置信区间.其次，采用线性回归模型的方法，分析输入数据特征对相关性估计值置信区间的影响.然后，针对置信区间的影响因素，提出对模型输入数据的筛选方案，并对置信区间进行优化.最后，提取相关性曲线的动态特征，分析神经元间相关性动态变化与朝向光栅刺激之间的关系.

1.2.1 神经元对相关性的估计

采用状态空间的对数线性模型初步估算神经元对的动态相关性，具体计算原理和步骤如下.

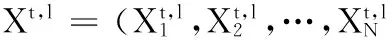
(1)

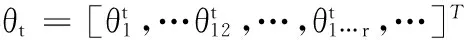
1.2.2 置信区间的优化

在EM算法计算模型参数的过程中，递归的贝叶斯滤波器给出了对数线性参数的后验分布，后验分布提供了参数θ的最优估计值，根据参数θ的后验分布，可以计算θ落在区间[a,b]内的后验概率(置信水平)，譬如1-α，即

P(a≤θ≤b|y)=1-α.

(2)

若给定置信水平为1-α，确定一个区间[a,b]使式(2)成立，则该区间为估计值θ置信水平为1-α的置信区间.

置信区间反映了贝叶斯估计值的可信范围，置信区间过大会降低模型估计值的精确度[14].置信区间受输入数据的波动性和发放率均值的影响：

1)发放率的波动性.神经元发放率的波动性采用标准差来衡量，对于神经元对，发放率的标准差定义为两个神经元发放率标准差的均值.

2)发放率均值.对于一个神经元对，某个朝向光栅下的发放率均值定义为两个神经元在刺激下的平均发放率.

1.2.3 相关性曲线的动态特性提取

笔者提取曲线的增减性和波动性特征，分析视觉刺激期间相关性曲线动态过程.

1)相关性曲线的增减性.采用线性回归方法，提取曲线拟合直线的斜率作为衡量曲线增减性的特征.拟合斜率为正值，表示刺激期间神经元间的同步作用逐渐增强，反之亦然.

2)相关性曲线的波动性.相关性曲线的波动性通过计算构成曲线的1 000个θ值的方差来衡量:

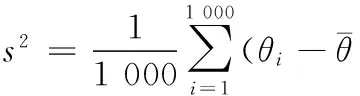
(3)

方差越大，神经元对的相关性曲线变化越剧烈，表明在刺激期间神经元间的同步作用变化的幅度越大，反之亦然.

1.2.4 神经元对的共同朝向响应强度

笔者根据共同朝向响应强度对光栅进行排序，为研究动态相关性特征与朝向光栅间的关系提供依据.

共同朝向响应强度反映了两个神经元在同一朝向下的响应特性，计算方法为

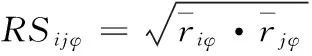
(4)

2 实验结果和分析

从郑州大学实验平台2012年7月到2013年7月的实验数据中选取4只大鼠(分别用A鼠、B鼠、C鼠、D鼠表示)，从每只大鼠选取5个刺激有效响应神经元(以数字1～5进行编号)，则来自每只大鼠的神经元对有10对，4只大鼠共40对神经元.

2.1 置信区间的优化

按照1.2.2节的方法，对输入数据特征和置信区间宽度做回归分析，其中置信水平1-α=0.95，如图2所示.

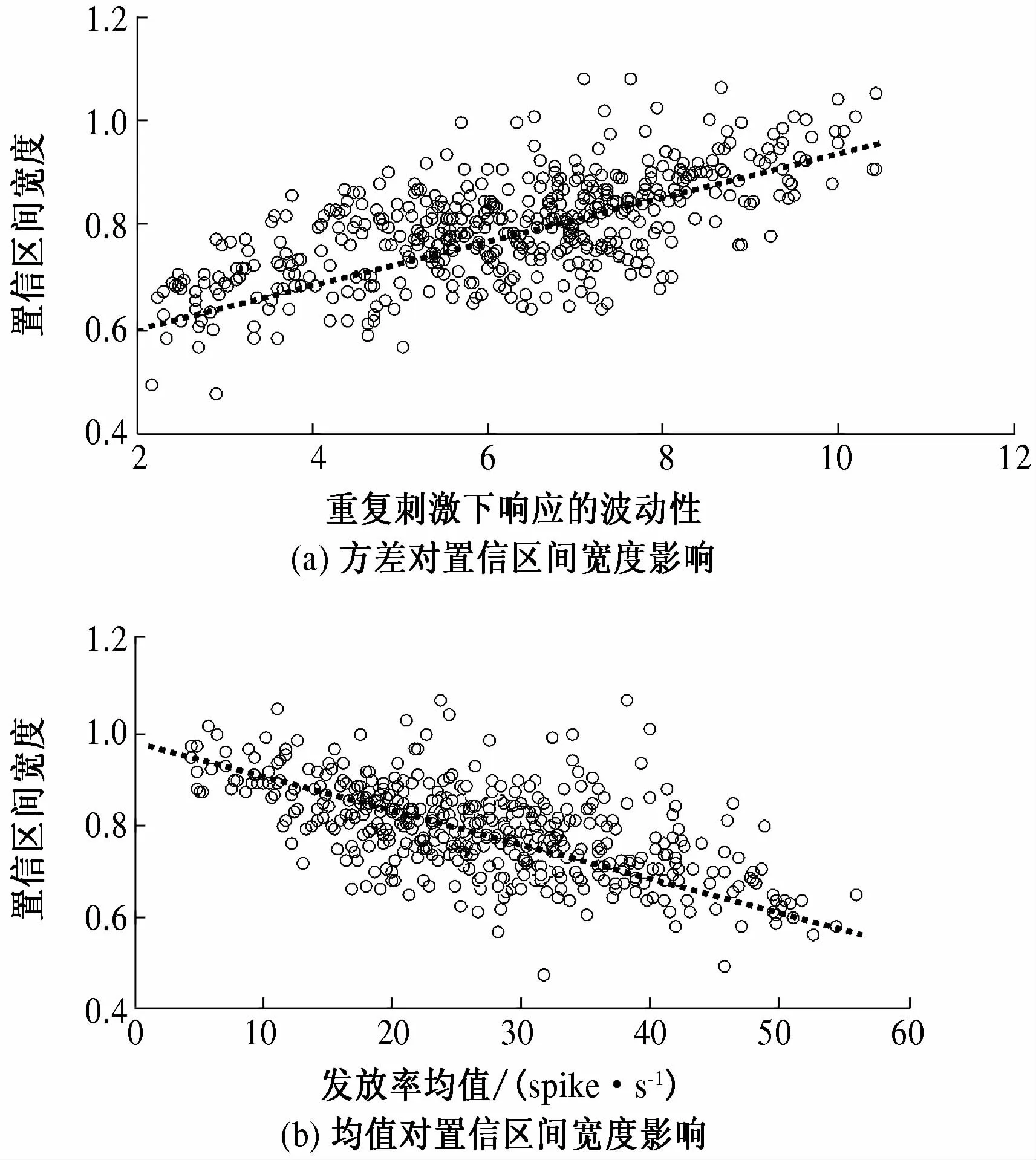
图2 模型输入数据特征对置信区间宽度的影响Fig.2 The influence of features of input dataon the width of confidence interval

因此，笔者对数据筛选的方案为：通过对重复实验下获取的数据的发放率进行分析，剔除发放率偏小的数据序列，实现对模型输入数据的筛选，有效地减小了置信区间的宽度，提高了模型估计值的精确度.

2.2 不同朝向光栅刺激下的动态相关性

朝向角度差为180°的光栅具有一定的空间对称性，为了提高不同朝向光栅下的神经元发放的差异性，对每一对神经元，选取实验12个朝向中连续的7个朝向，并按照共同朝向响应强度对每个神经元对的7个朝向由强到弱排序.选取40对神经元在光栅刺激下采集的锋电位发放序列，利用筛选后的数据作为模型的输入数据.

首先，研究不同朝向刺激下神经对的相关性强度的变化.分别采用状态空间对数线性模型和常规互相关图法，计算不同朝向光栅下相关性曲线的幅值均值和互相关图的峰值，并按照朝向排序RS，对相应排序下的40个神经元对的幅值均值和峰值叠加平均，如图3(a)、(b)所示.

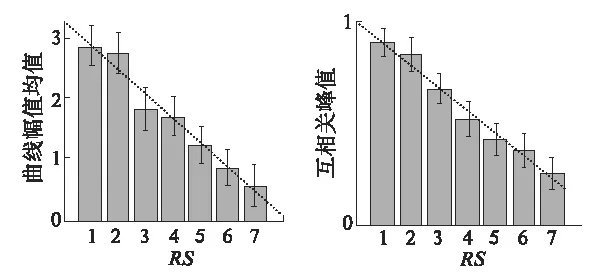
(a)模型法的结果 (b)互相关图法的结果 图3 神经元对采用两种方法计算的相关性强度Fig.3 Correlation values of paired neurons acquired by two different methods

对比图3(a)和图3(b)发现，两种方法的计算结果具有一致性：对于一个神经元对，它在不同朝向光栅下的相关性强度随着共同响应强度的减小而减小.这说明了该模型能够有效地估计神经元间的相关性，同时表明神经元间的同步作用强度能够有效地编码光栅刺激信息.

然后，分析不同朝向光栅刺激下相关性曲线的增减性.利用筛选后的数据，计算40对神经元在各自7个朝向刺激下的相关性曲线的拟合斜率(共280个值，拟合优度确定系数R=0.783 0±0.056 4，标准差E=0.263 7±0.040 9)，正负值分布统计结果如图4所示.

图4 神经元对在排序朝向下斜率正负值统计图Fig.4 Statistical chart of fitting slopes from paired neurons under 7 sorted orientations

图4中，横轴表示按照RS排列的朝向光栅，纵轴表示对应排序朝向光栅下拟合斜率正值和负值的统计个数，其中94.3%(264/280)的斜率值为正.从图4可知，在朝向光栅刺激期间，大部分神经元对的相关性逐渐增强，即同步作用逐渐增强.在共同响应强度较小(RS排序靠后)时，共有16种情况下的神经元对的相关性逐渐减弱，通过分析构成这些神经元对的两个神经元的最优朝向角度差Δα，发现Δα均为90°，即两个神经元的最优朝向正交.

最后，分析不同朝向光栅下相关性曲线的波动性，如图5所示.横轴表示按照RS排列的朝向光栅，纵轴表示对应排序朝向光栅下40个神经元对的相关性曲线方差的均值和标准差，虚线表示方差均值的拟合直线.

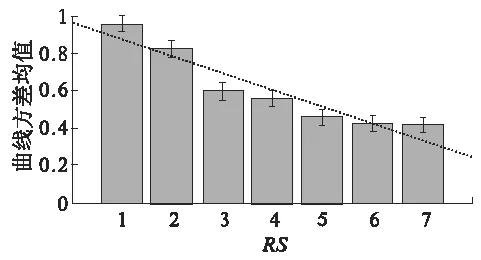
图5 40个神经元对在排序朝向下曲线方差均值Fig.5 Mean of variances of curves for 40 paired neurons

从图5可知，对于一个神经元对，它在不同朝向光栅下的同步作用波动的幅度随着共同响应强度的减小而减小.

3 结论

(1)模型估计值置信区间受到输入数据发放率波动性和均值的影响，采用剔除发放率偏小的数据序列的筛选方案，能够有效地缩小置信区间的宽度；(2)对于一个神经元对，它在不同朝向光栅下的相关性强度随着共同响应强度的减小而减小；(3)在刺激期间，神经元间的同步作用的增减性对朝向刺激信息具有编码作用，当神经元的最优朝向正交且受到共同响应强度较弱的朝向光栅的刺激时，神经元对的同步性会逐渐降低，而在其他情况下，神经元对的同步性增强；同时，笔者还发现一个神经元对在不同朝向光栅下的同步作用波动的幅度随着共同响应强度的减小而减小，这说明神经元对同步作用的波动幅度也编码了朝向光栅刺激信息.

由于时间的关系，笔者只研究了成对神经元之间动态相关性的变化规律，进一步的工作还需要研究更高阶次的神经元间的相关性.

[1] 寿天德.视觉信息处理的脑机制[M].合肥:中国科学技术大学出版社, 2010:18.

[2] BERENS P, ECKER A S, COTTON R J, et al. Fast and simple population code for orientation in primate V1[J]. the Journal of Neuroscience, 2012, 32(31): 10618-10626.

[3] BRUNO B AVERBECK, DAEYEOL L. Coding and transmission of information by neural ensembles[J]. Trends Neurosci, 2004, 27(4):225-230.

[6] BHARMAURIA V, BACHATENE L, CATTAN S, et al. Synergistic activity between primary visual neurons[J]. Neuroscience, 2014,268:255-264.

[7] SAMONS J M, ZHOU Zhi-yi, BERNARD M R, et al. Synchronous activity in cat visual cortex encodes collinear and cocircular contours[J]. Journal of Neurophysiology, 2006, 95(4):2602-2616.

[8] FERNANDO M, SMITH K A, MATTHEW A. et al. The role of correlations in direction and contrast coding in the primary visual cortex[J].Neuroscience, 2007, 27(9):2338-2348.

[9] REED J L, POUGET P, QI Hui-Xin, et al. Effects of spatiotemporal stimulus properties on spike timing correlations in owl monkey primary somatosensory cortex[J]. J Neurophysiol, 2012, 108(12):3353.

[10]SHIMAZAKI H, AMARI S-I, BROWN E N, et al. State-space analysis of time-varying higher-order spike correlation for multiple neural spike train data[J]. PLoS Comput Biol, 2012, 8(3):233-239.

[11]师黎，杨振兴，王志忠，等.基于PCA和改进K均值算法的动作电位分类[J].计算机工程, 2011, 37(16):182-187.

[12]万红，郜丽赛，牛晓可.基于匹配小波变换的初级视皮层神经元锋电位分类[J].郑州大学学报：工学版，2011，32(3)：90-95.

[13]MARTIGNON L, DECO G, LASKEY K, et al. Neural coding: higherorder temporal patterns in the neurostatistics of cell assemblies[J]. Neural Comput, 2000, 12(11): 2621-2653.

[14]陶靖轩，李秀兰. 贝叶斯区间估计[J]. 中国计量学院学报，2002,13(2)：103-108.

The Analysis of Dynamic Correlation Between Neurons Based on State-space Log-linear Model

SHI Li, XU Kun-feng, NIU Xiao-ke

(School of Electrical Engineering, Zhengzhou University, Zhengzhou 450001, China)

The research on correlation between neurons is the foundation to understand the mechanism of information transmission and coding of neuronal population. A novel method called state-space log-linear model was used to estimate the dynamic correlation between paired neurons, and data sieving methods were proposed to improve the accuracy of model results for the effects of input data characteristics on the confidence interval of the model estimated values. By extracting the characteristics of dynamic correlation curves, changing characteristics of paired neurons’ correlation was analyzed and then the effect on information coding of visual stimulus from synchronization between paired neurons was studied. Experimental verification was carried out in the primary visual cortex of anesthetized rats. The results show that: the accuracy of the estimated value of the model can be improved by removing the data with small firing rates, and synchronization between paired neurons encodes the information of different grating stimuli.

state-space log-linear model; dynamic correlation; information coding; synchronization

2014-08-25；

2014-11-03

国家自然科学基金资助项目(U1304602)；河南省重点科技攻关计划资助项目(122102210102)

师黎(1964-)，女，河南郑州人，郑州大学教授，博士生导师，研究方向为智能检测，生物信号处理,E-mail:shili@zzu.edu.cn.

1671-6833(2015)01-0001-05

TN911.7

A

10.3969/j.issn.1671-6833.2015.01.001