张弦梁结构张拉力确定方法研究

李静斌，洪彩玲，张 哲，李素洁

(1.郑州大学 土木工程学院,河南 郑州 450001; 2.濮阳职业技术学院 建筑工程系,河南 濮阳 457000)

张弦梁结构张拉力确定方法研究

李静斌1，洪彩玲1，张 哲1，李素洁2

(1.郑州大学 土木工程学院,河南 郑州 450001; 2.濮阳职业技术学院 建筑工程系,河南 濮阳 457000)

张弦梁结构属于预应力钢结构的一种，在进行拉索预应力导入过程中必须保证施工过程的安全性和完工时的受力状态满足设计要求.因此，必须对张拉索进行张拉过程的索力优化分析和研究，保证对整个施工过程的安全控制.以双向张弦梁为例对比了3种优化方法对张弦梁结构的适用性.经计算分析，得出了张力补偿法为适用于张弦结构张拉力确定的最优方法.结合鹤壁市体育馆预应力空间桁架钢屋盖结构，采用张力补偿法进行了该结构施工阶段分析，得出了高强钢索的内力发展变化规律，验证了张力补偿法在实际大型预应力空间钢结构中的适用性.

空间结构；张弦梁；张拉力；张拉顺序；索力优化

0 引言

张弦梁结构(简称BSS，Beam String Structure)主要由刚性梁、柔性下弦及撑杆构成[1]，属于典型的预应力钢结构.刚性梁在整个结构体系中是刚性的压弯构件，可由多种形式构成，例如最简单的直线形梁、拱形梁和桁架结构等；柔性下弦多采用高强度钢索或高强度钢棒构成；撑杆多采用受压性能较好的构件，如钢管等.张弦梁结构是由刚性构件和柔性拉索组成的自平衡结构体系的独特受力模式，直接导致其与普通的钢结构在施工控制和有限元分析的不同，随着对柔性索张拉力的导入，结构体系也随之变化，并且不同施工方法和施工顺序，都会对结构最终受力状态产生影响.因此，对于拉索张拉力的控制和张拉批次的划分显得尤为重要.笔者结合鹤壁市体育馆应力空间桁架钢屋盖结构，采用张力补偿法进行了该结构施工阶段分析，验证了张力补偿法在实际大型预应力空间钢结构中的适用性.

1 索力优化方法

索力优化可根据结构的具体形式选择不同的优化方法，在预应力钢结构中已相对成熟的索力优化方法有从结构变形控制的形变控制法[2]、有从施工顺序考虑的迭代优化法[3]和倒退分析法[4]等，还有从计算精度要求控制的改进遗传算法[5]、改进倒退分析法和修正循环迭代法[6]等.然而并不是所有的预应力结构都能采用同一种方法.针对张弦梁结构，简单验证逆分析[7]、位移补偿法[8]和张力补偿法[9]对其索力优化的适用性.

1.1 双向张弦梁有限元模型

一双向张弦梁结构，上弦为工字形钢梁，下弦为通过长2 m、高1 m的撑杆相连的高强钢索，结构每个方向跨度为20 m.上弦截面特性HN800 mm×300 mm×14 mm×26 mm，撑杆采用钢管Φ32 mm×3 mm，钢材均为Q345B；下弦是直径为28 mm的圆形截面高强钢索，抗拉强度为1 670 MPa.每跨张弦梁的一端为固定铰支座，另一端为滑动铰支座，每跨张弦梁的构造相同.算例结构简图、节点构造连接及MIDAS/Civil中的有限元模型见图1～图3所示.

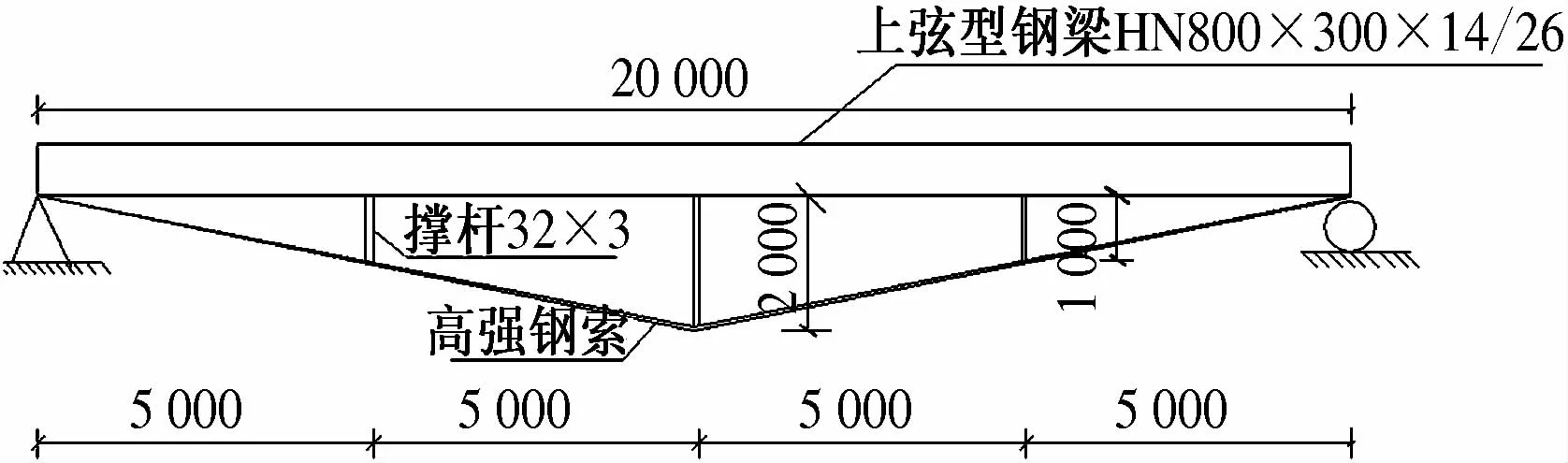
图1 双向张弦梁结构图Fig.1 Two-way beam string structure

1.2 逆分析法

按文献[7]方法对双向张弦梁进行索力优化分析.该结构的张弦预应力在使用状态时的内力均为150.7 kN，每根型钢梁下均有一根张拉索，共4根高强钢索，划分为4批，每批索编号见图3.正常的施工顺序是从1批张拉至4批.在逆分析求张拉索的内力时，逆着施工顺序进行拉索的模拟拆除.拆除的顺序4、3、2，在拆除索的过程中记录剩余每根索的内力，最终可得正常施工顺序时所应施加的预应力，计算结果见表1.表中N1～N4代表各拉索内力.

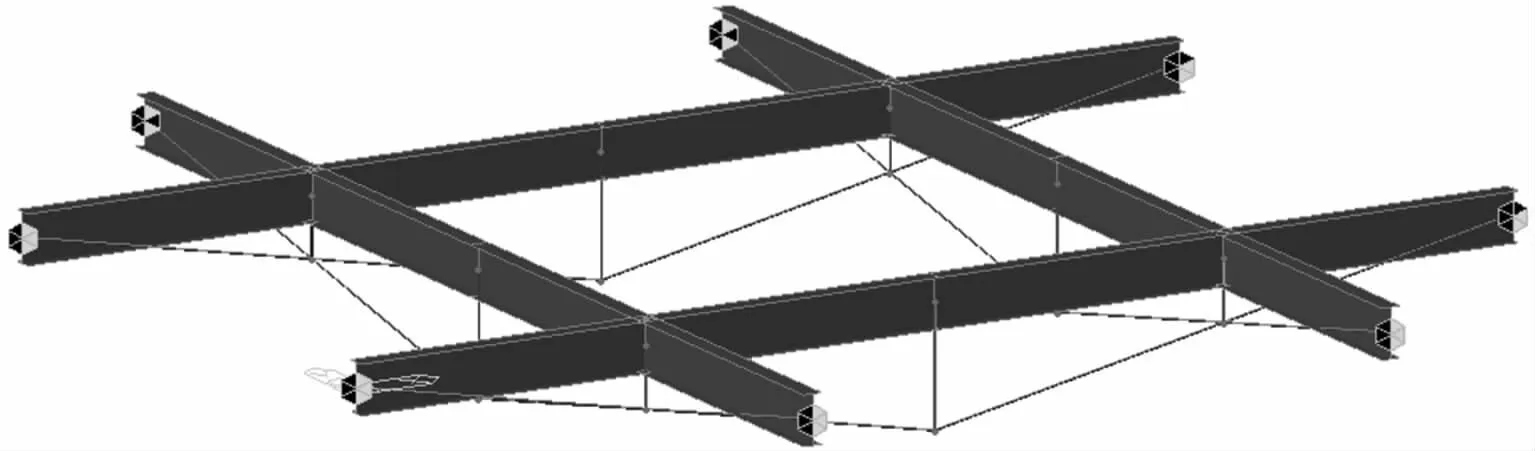
图2 双向张弦梁体系算例有限元模型Fig.2 The FEM of two-way beam string structure

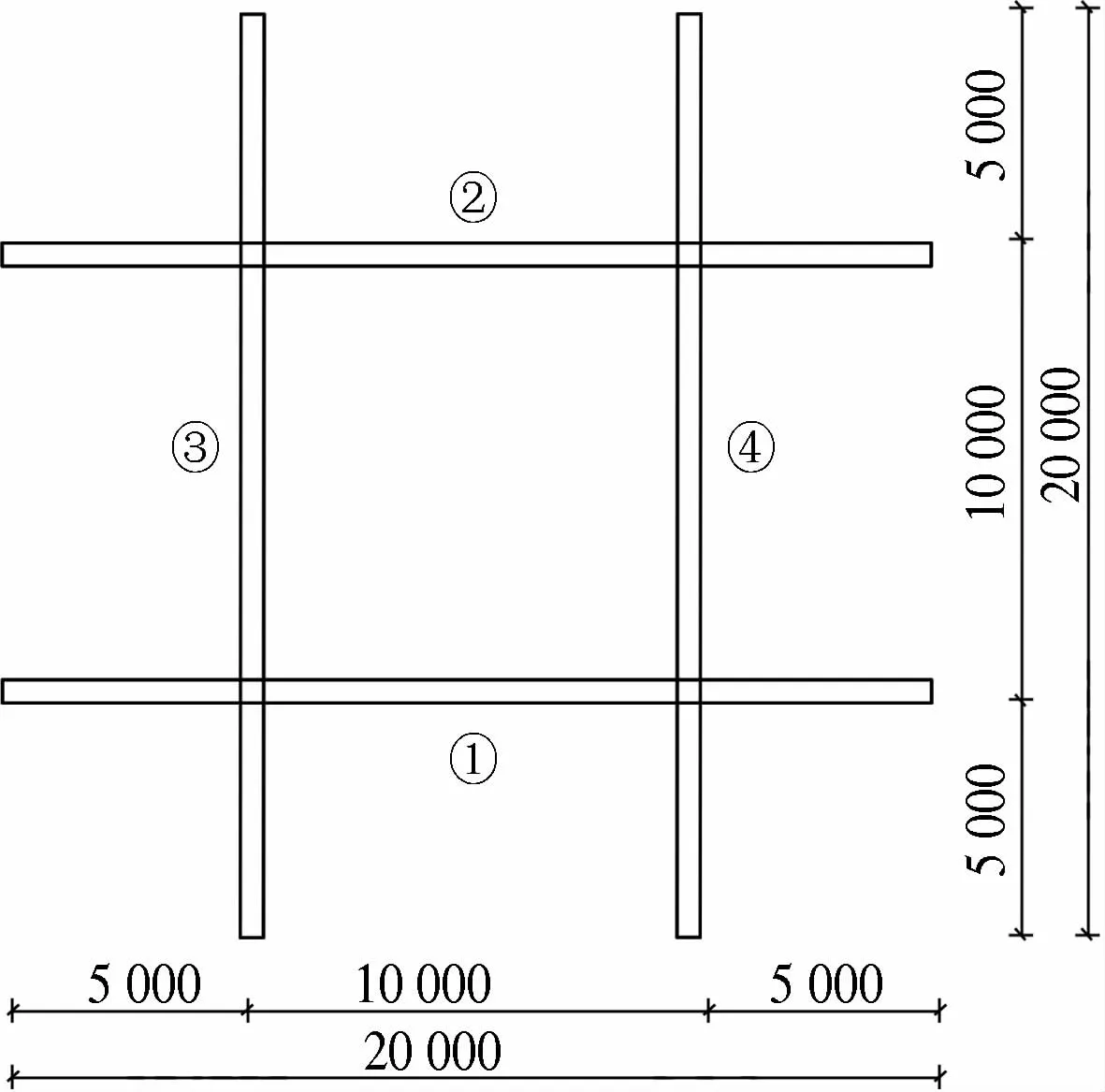
图3 结构俯视图及拉索编号Fig.3 The overlooking of the model and cable position 表1 双向张弦梁逆分析结果Tab.1 Results of two-way beam string structure inverse analysis

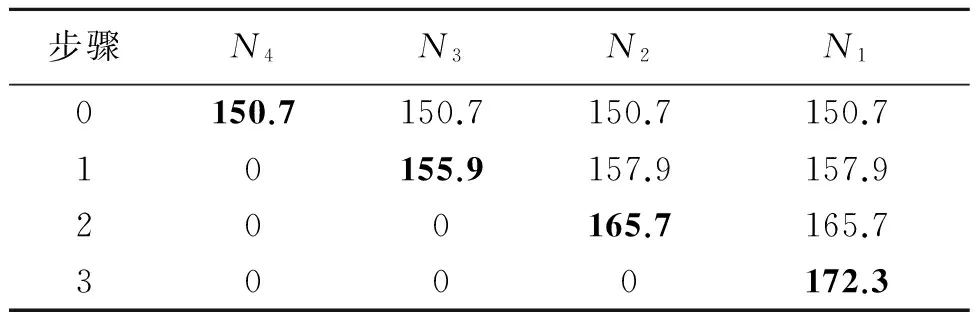
kN

通过逆分析得出每根索应施加的预应力见表1对角线黑体数字所示.为验证索预应力是否满足实际施工时的结构内力要求，将逆分析得出的预应力值按照正常的施工顺序加载到相应的张拉索上，验证完工后结构的张拉索内力是否为150.7 kN.经计算得到每根索的拉力如图4所示.

图4显示计算的结果并不等于结构设计状态的150.7 kN，最大误差约为12.4%.在文献中是以柔性的张力结构为例进行的逆分析索力优化，在整个优化过程中，索力的增减与杆件刚度的增减是一致的.这是因为柔性结构只有在施加预应力时结构才具有一定的刚度，一旦将预应力减小或撤除，则结构的刚度也会随之变化或消失.但在张弦梁结构中，结构的逆序只是在张拉索的过程中进行逆序，此刻上部的刚性结构的刚度和内力并没有随着索力的增减而增减，即结构的刚度变化只是索力部分的变化，上部刚性梁的刚度并没有发生变化，导致所谓的逆序并不是严格意义上的施工全过程的逆序.故用逆分析法得出的索力优化结果与设计值存在一定的偏差.

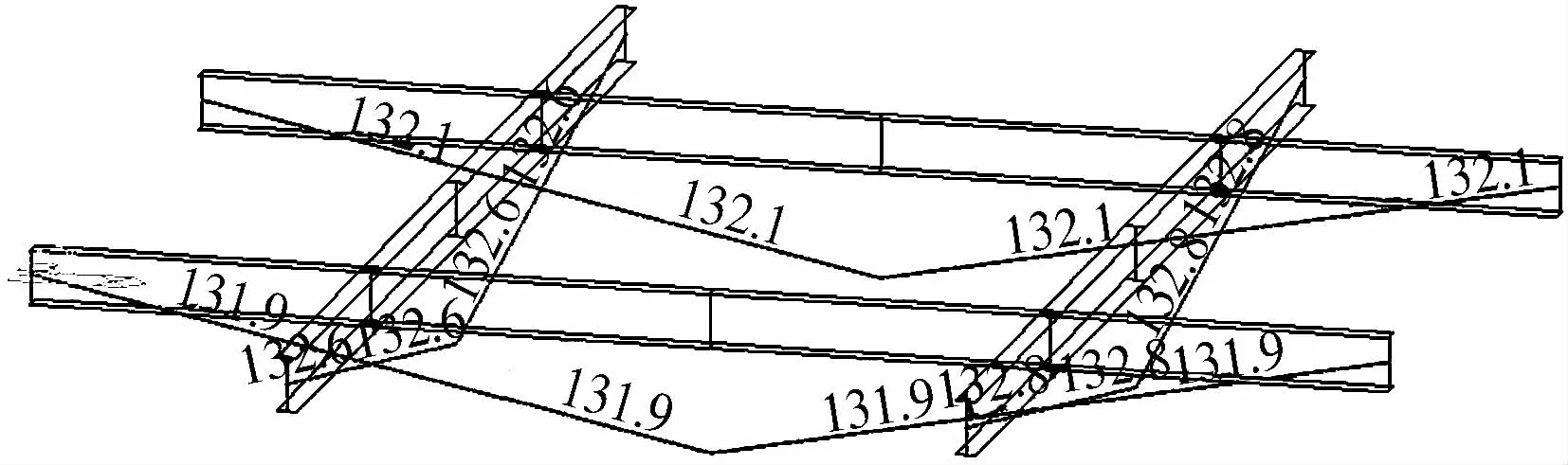
图4 逆分析所得索力验证结果Fig.4 The verification results of inverse analysis

1.3 位移补偿法

位移补偿法是从变形上控制结构的张拉力，为保证张拉完毕后结构几何位形满足实际要求，应从控制节点位移着手.按文献[8]，第1次循环计算时以结构所有控制节点位移坐标的设计值作为初始循环值；然后张拉每批索，使控制节点的位移值等于设计值，并记录其他控制节点的位移值，完成第1次循环计算.这时，每个控制节点的位移与设计值之间存在一个差值，将该差值与设计值相加，作为第2次循环计算的初始值，依次循环计算，直至各个控制节点在计算完成后的位移变化量接近或等于设计值.并记录下达到位移设计值时各批索的张拉力大小，即得出张拉高强钢索时的索力最优值.

结构的设计状态控制位移以结构撑杆处的最低点为控制位移，如图5中点18，26，20，27控制点的设计位移均为11.371 mm.进行第1次循环计算，使张拉钢索时的控制点位移在张拉相应批次时等于其设计状态位移，同时记录其他批次,此时结构的控制点位移如表2所示.

该算例1次循环计算即可得到计算结果.应注意，对于简单结构采用该方法可获得精确结果，且循环计算的次数也不多.同时对于杂交的张弦结构，结构的刚度由张拉钢索和上弦刚性构件共同组成，在进行节点位移控制时，需要保证结构的位移一致性的变化，即下弦控制节点处与上弦刚性梁连接处的位移变化一致，在进行结构的有限元建模时对于单元节点连接处的模拟要符合结构的受力要求.

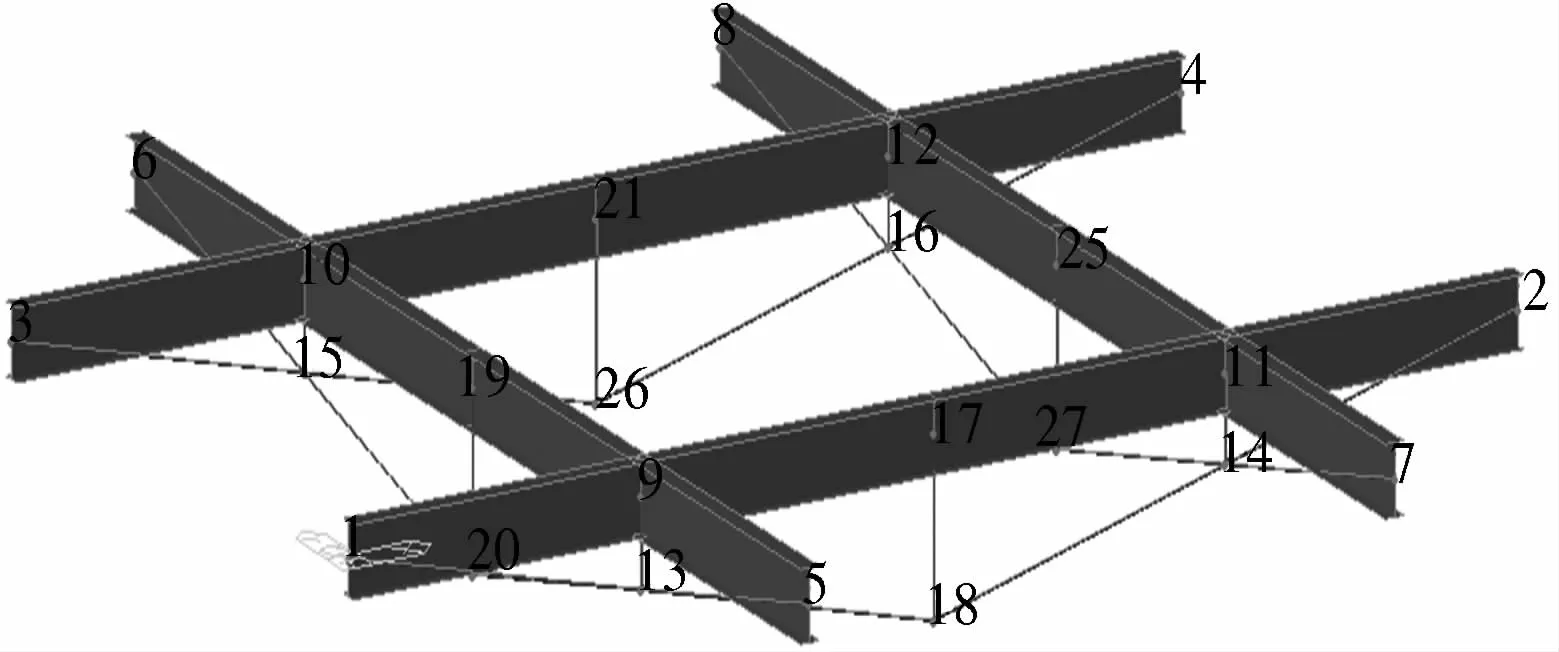
图5 位移补偿法节点编号Fig.5 The node number in the displacement compensation analysis method 表2 第1次循环计算节点位移Tab.2 The node displacement in step 1 cycle

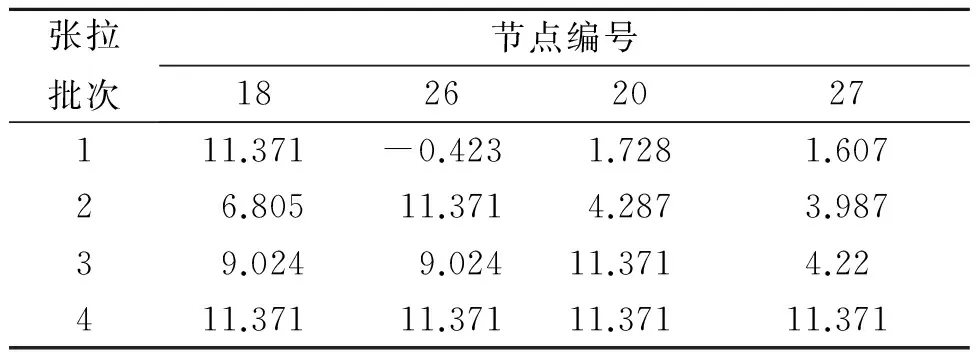
mm

1.4 张力补偿法

张力补偿法的思想与位移补偿法的思想相似，也是进行循环的计算.但比后者更为直观.该

方法是直接以力的变化作为控制量，不需要再以位移作为基本量进行转化，具体原理可参考文献[9].结构成形后每根索所要达到的控制值作为首次计算的基本数据，首先对结构中的高强钢索按照实际的施工工序进行分批，然后模拟施工过程中边界条件随施工的进度发展.进行各批索的张拉，张拉完毕后，记录该过程完成后每根索的内力.此时各索内力与设计值之间存在一个差值，比较该差值与设计值之间的百分比，验算是否满足工程精度要求.若不满足，将该差值叠加到初始值上进行下轮计算，直到计算所得结果满足设计值要求.

双向张弦梁索力设计值为每根索150.7 kN，计算过程记录如表3所示.表3中计算结果显示，当进行第3次循环计算以后，结构的内力值与设计值的差值百分比为0.33%，满足工程的精度要求.那么第3次循环计算的初始值162.2 kN就是结构在进行预应力输入过程中的张拉力控制值.用张力补偿法最大的好处是优化过程也是内力控制的过程.因为在最后一步满足工程精度要求的结果，也就是优化过程的最后一次循环计算，跟踪这个过程的索的内力变化，防止在张拉过程中索力过大，造成结构的失稳破环或其他形式的破坏.

表3 张力补偿法计算过程与结果Tab.3 The calculating process and results of tensile force compensation analysis method kN

1.5 索力优化方法总结

通过3种索力优化方法对双向张弦梁进行索力优化分析，得到逆分析法所得的张拉控制值偏小，与设计值的最大偏差达到12%；位移补偿法得到的结果与设计值一致，但是需要特别注意的是，应用该方法对于简单的结构可以很快地得到优化结果，对于复杂的杂交空间结构，需要掌握的控制点位移较多，需要进行迭代的次数就会增多，因此要慎重选择该方法；张力补偿法思路简单，从张拉力角度直接进行优化分析，需要迭代的次数不多，由于笔者所举例子拉索数量少，各索之间张拉力的影响不明显，当拉索数量较多时，张力补偿法在优化过程中还可充分考虑张拉过程中拉索之间内力的相互影响，适合张弦结构的索力优化.

2 工程实例验证

2.1 工程概况

鹤壁市体育馆位于鹤壁市朝歌路与兴鹤大街向北200 m路西，造型呈“马蹄形”.基础为人工挖孔桩.结构形式为钢筋混凝土框架、劲性混凝土及钢结构为一体的混合结构，屋面为预应力空间管桁架，屋面板为铝镁锰板，外墙由153只铝单板制成的千纸鹤组成.建筑面积16 666 m2，其钢屋盖结构图如图6所示.

2.2 有限元建模

采用MIDAS/Civil有限元软件建立鹤壁市体育馆屋盖钢结构有限元计算模型，在进行钢索张拉过程中，实际张拉索时，屋盖周边支撑情况是环向方向受到约束，径向方向在一定范围内可进行滑动，这也为施工完成后结构的索力在温度等其他效应影响产生变形时有一个伸缩变化的范围.为了更加准确地定义适合该变化的边界条件，应对端部的约束位置进行单元局部坐标的定义，以便对节点进行支座的约束.另外，对于中心凸起桁架下的胎架支撑的模拟采用简单的一般支撑，为中心刚性环的吊装提供临时支撑.

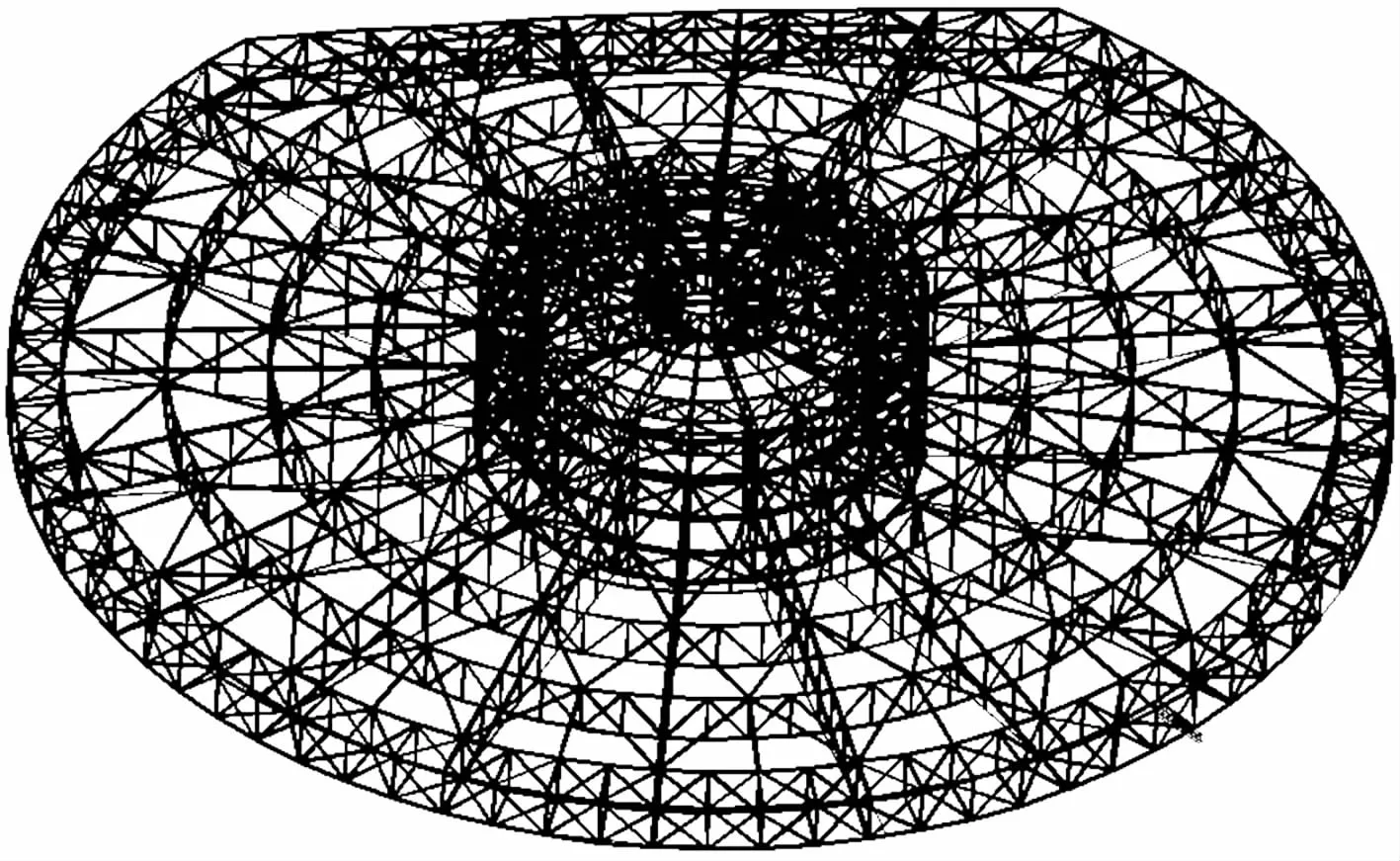
图6 鹤壁市体育馆钢屋盖结构Fig.6 Steel roof structure of Hebi City stadium

根据工程实际，将屋盖钢结构分为管桁架、撑杆和拉索、第1批索、第2批索、第3批索、第4批索、第5批索7个结构单元组；将边界划分为边支座、中心支撑2个边界组；荷载组划分为自重、拉索力20% 1批、拉索力20% 2批、拉索力20% 3批、拉索力20% 4批、拉索力20% 5批、拉索力100% 1批、拉索力100% 2批、拉索力100% 3批、拉索力100% 4批、拉索力100% 5批共11个荷载组.根据在施工中的预应力导入顺序，将整个过程划分为12个阶段.

2.3 施工阶段的索力张拉优化分析

在进行钢索的张拉过程中要实时监控每根索的内力变化，防止某根索或某批索的张拉力过大，超过钢索的承载极限.施工阶段的前6个阶段是结构在边支撑和中心支撑上对结构进行设计值的20%进行初张拉，在这个过程中索的内力能保证处于设计值允许的范围内，但是在结构卸载即中心支撑撤出后的钢索拉力和上弦管桁架的内力和应力也应控制在材料允许的范围内.

由于在张拉20%初张力是在胎架上进行张拉，有中心支撑的作用，使得在张拉过程中不会出现某根索的超张拉，也不会出现某根索的应力松弛现象.因此，拉索内力控制的核心关键在中心支撑撤除后，再进行100%张拉时对各个索在张拉过程中的索力变化，要保证避免出现较大的超张拉和应力松弛现象.张拉过程的仿真分析结果如图7所示，图中给出了采用张力补偿法分析得到的第5批4根高强钢索随施工阶段进展的内力变化图.图7中横坐标CS1～CS12代表预应力导入的12的施工阶段，纵坐标代表索力.其他各批次张拉的高强钢索的内力变化规律与其相似，限于篇幅，不再一一给出.

从钢索内力随施工阶段的变化图可知，每根索的内力基本控制在设计要求的范围内.另外还可看到在进行张拉的过程中，每批索的内力都在随着施工阶段的推进受到其他索的内力影响，并且对于第一批索的张拉要特别注意，从内力变化趋势图中可以看到，基本是呈上升趋势.所以在施工时一定要把握好第一批索的内力控制，防止在后续张拉索的进程中超张拉过度.

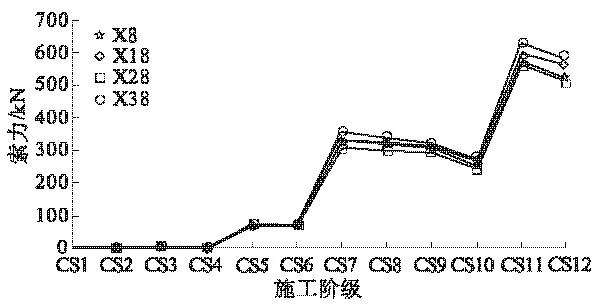
图7 第5批高强钢索随施工阶段的内力变化图Fig.7 The internal force variation of the fifth high strength steel wire ropes in construction

3 结论

通过采用张弦梁简单结构选定索力优化方法，并通过鹤壁市体育馆预应力空间钢桁架结构的施工阶段分析，可得出以下结论.

(1)逆分析法对于上下弦刚度相差较大的张弦结构所得到的优化结果差异超出了工程精度的要求，因此在实际运用中要充分考虑各方面因素对优化结果的影响，保证优化结果的准确性和精确度满足要求；

(2)位移补偿法对张弦梁结构进行索力优化可以得到精确的结果，但是对于复杂的结构或拉索数量较多的结构，需要计算的控制点数量多，则需要更多次的循环迭代计算，因此，在采用该方法时需要注意这方面的计算要求，同时还要注意节点位移变化和力变化之间的关系是否可以直接转换，保证所得结果的有效性；

(3)张力补偿法思路简单，对拉索数量较多的张弦梁结构，可充分考虑张拉过程中索力之间的相互影响，需要迭代的次数不多，体现了该方法对于张弦梁结构的普遍适用性.通过张力补偿法在大型钢结构工程中的计算分析验证，证明该方法的适用性和有效性.

[1] 陆赐麟．现代预应力钢结构(修订版)[M]．北京：人民交通出版社，2007．

[2] 刘晟，薛伟晨，大跨度预应力张弦梁施工控制技术研究[J] ．建筑结构，2009，39(5)：49-53．

[3] 李传夫，李术才．迭代优化算法在大跨拱桥线性控制中的应用[J] ．山东大学学报：工学版，2008，38(3)：23-27．

[4] 吕晶，郭彦林．劲柔索张拉穹顶结构施工仿真分析[J] ．施工技术，2007，36(3)：18-20．

[5] FREDRICSON H，JOHANSEN T，KLARBRING A．Topology optimization of frame structures with flexible joints [J]．Struct Multidisc Optim ，2003，25(3)：199-214．

[6] 吕方宏，沈祖炎．修正的循环迭代法与控制索原长法结合进行杂交空间结构施工控制[J]．建筑结构学报，2003，26(3)：92-97．

[7] 李波，杨庆山．张力结构的施工计算[J] ．北京交通大学学报，2007，31(1)：93-96.

[8] 张国发，董石麟．位移补偿计算法在结构索力调整中的应用[J] ．建筑结构学报，2008，29(2)：39-34.

[9] 卓新，石川浩一郎．张力补偿算法在预应力空间网格结构张拉施工中的应用[J] ．土木工程学报，2004，37(4)：38-40.

[10]洪彩玲．大跨度预应力空间钢结构施工过程分析与索力优化研究[D] ．郑州：郑州大学土木工程学院，2013．

The Inquiry of Tension Method for the Beam String Structure

LI Jing-bin1， HONG Cai-ling1， ZHANG Zhe1， LI Su-jie2

(1.School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China; 2.Department of Building Engineering, Puyang Vocational and Technical College, Puyang 457000, China)

The beam string structure belongs to a kind of pre-stressed steel structure, in the pre-stressed import process the cable must be ensured the safety and completion of the construction process of stress state must meet the design requirements. Therefore, the tension cable tensioning process cable force optimization analysis and research is useful to guarantee for the safety of the construction process control. Two-way beam string is used as an example, to compare the three kinds of the applicability of beam string structure optimization method. Through calculation and analysis, it is concluded that the tension compensation method is suitable for a optimal method to determine the tension of string structure. Combination of Hebi city stadium pre-stressed steel roof space truss structure, the tension compensation method is used for the analysis of structure construction stage, it is concluded that the development of internal force variation law of high strength steel wire rope, tension compensation method is verified in actual large the applicability of the pre-stressed space steel structure.

space structure； beam string structure； tension； tensioning sequence； cable force optimization

2014-09-07；

2014-11-10

国家自然科学基金资助项目(51478437)

李静斌(1973-)，男，天津静海人，郑州大学副教授，博士，主要从事结构计算分析方面的研究，E-mail:lijingbin@zzu.edu.cn.

1671-6833(2015)01-0061-05

TU394

A

10.3969/j.issn.1671-6833.2015.01.015