汽轮机叶型的三维数值模拟及优化

周俊杰，王梅玲，郭朋飞，王定标

(郑州大学 化工与能源学院，河南 郑州 450001)

汽轮机叶型的三维数值模拟及优化

周俊杰，王梅玲，郭朋飞，王定标

(郑州大学 化工与能源学院，河南 郑州 450001)

以25 MW凝气式汽轮机的某级叶片为研究对象，利用ANSYS Workbench平台中的旋转机械分析系统对该级叶片进行了静、动联合三维数值模拟优化.结果表明，优化后叶片压力系数分布较好，降低了叶片表面压差分布，有效控制径向二次流损失；总压损失系数有所减小，平均总压损失系数降低1 %；等熵效率由原来的92.099%提高至93.157%.优化后的叶型明显提高了气动性能，降低叶型能量损失，增加了汽轮机效率.

汽轮机；叶片；气动性能；数值模拟

0 引言

汽轮机是一种以过热蒸汽为动力，并将蒸汽的热能转化为机械能的旋转机械.设计高性能的蒸汽轮机，是目前叶轮机械领域技术研发的重要目标.汽轮机级内损失主要有型线损失、漏气损失、湿气损失、鼓风摩擦损失等[1].

在国内汽轮机的设计中，目前更多的是应用CFD软件为主，辅以必要的实验对现有叶片进行优化设计，从而节省经费和减少研制时间.MHI公司利用CFD软件对165 MW汽轮机叶片和汽封进行优化，最终得到性能良好的低压级叶片和汽封[2].岳国强等[3]对两套具有不同前缘直径和分布的叶栅进行对比吹风试验，结果表明选择适当的前后缘直径及合理匹配出口逆压段长度与逆压梯度值，可以有效地减少叶栅的二次流损失.薛彦光[4]利用CFX对300 MW汽轮机高压级静叶栅流场进行数值模拟，并分析了叶栅通道二次流发展特点.崔海涛[5]、王定标等[6]对汽轮机进行了三维数值模拟，并根据模拟结果对叶片进行了优化设计.

笔者主要借助ANSYS Workbench平台中的旋转机械分析系统软件，分析叶片间内流体的流动，研究叶型对流道内流体的影响，从而实现叶型优化，减少级能量损失，提高汽轮机效率.

1 数学物理模型

1.1 物理模型

研究对象为轴流式25 MW凝气式汽轮机某级叶片，气动分析时只考虑单静叶、单动叶结构.表1为叶片物理结构详细参数，图1为汽轮机结构图.

图1 汽轮机结构Fig.1 Structure of steam turbine

1.2 数学模型

汽轮机叶片间流动通道内的流动满足质量、动量以及能量守恒方程.

质量守恒方程[7-8]：

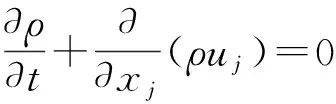
(1)

动量方程：

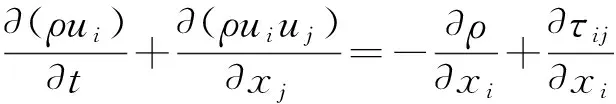
(2)

式中:ρ为密度；t为时间；ui,uj分别为i方向、j方向上的速度；τij为黏性应力.

能量方程：

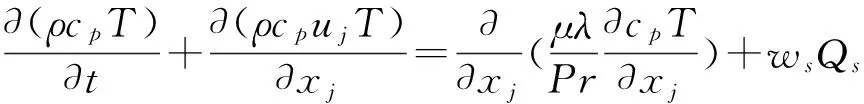
(3)

式中:Cp为比热容；T为温度；最后一项表示其他形式导入的能量.

1.3 网格划分及边界条件

笔者模拟汽轮机级内的流动性能，为了取消前、后级对该级性能的影响，保证流场的稳定性，分别对静、动叶的前后端均作适当的延长处理.采用H/J/C/L-Grid拓扑结构，生成网格后的节点总数为120 000.图2(a)为计算流道三维模型图，图2(b)为计算区域网格示意图.

表1 叶型安装参数Tab.1 Parameters of blade

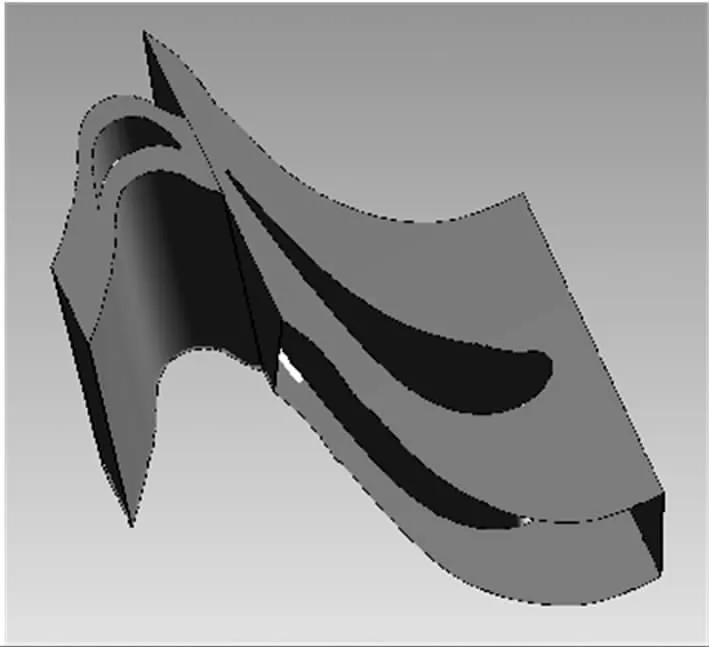
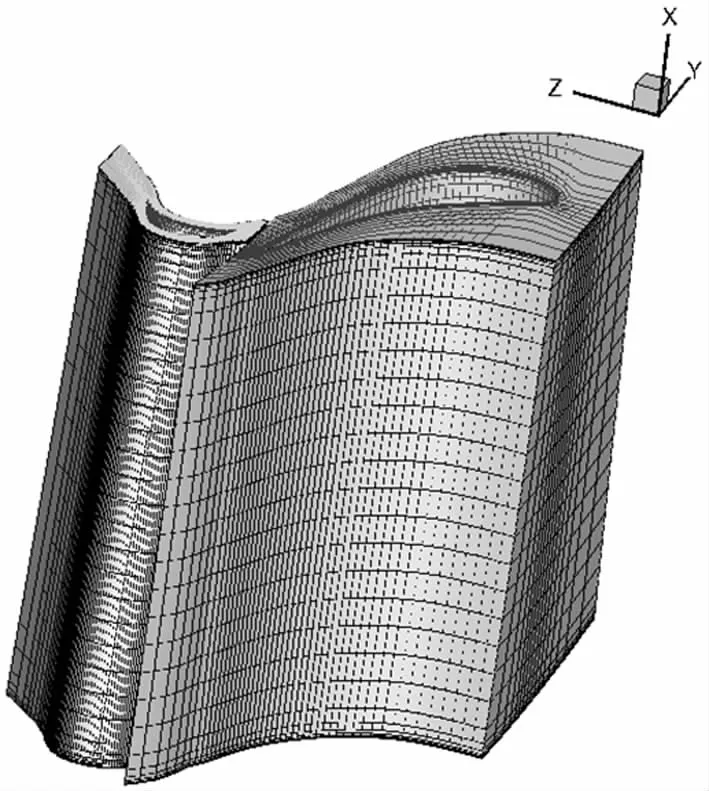
(a)计算流道三维模型 (b)计算区域网格示意图 图2 计算及网格模型Fig.2 Computation and Mesh model

选用P-Total Inlet P-Static Outlet模式的边界条件、Frozen Rotor交界面模式，来流方向垂直于进口截面.具体参数设置为：进口总压0.088 9 MPa，出口静压0.050 99 MPa，进口总温369.5 K.

1.4 工质属性

为更好地模拟实际状况，这里采用平衡态的水蒸气.首先在CFX中分别创建单相水和水蒸气，然后再通过设置参数的方式建立平衡态的水蒸气，定义单相水和水蒸气的最高温度为500 K，最低压力为0.01 MPa，最高压力为0.45 MPa，最大点数为100，定义单相水最低温度为250 K，水蒸气的最低温度为273.15 K.

2 计算结果分析

2.1 叶型表面静压系数分析

叶片表面静压系数计算表达式为

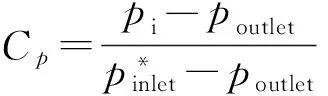
(4)

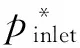
图3为原始工况下静、动叶片的压力系数分布曲线图.由图可以看出，在静叶0～0.8轴向位置处，优化叶型压力面上的压力与原始叶型基本一致，而吸力面压力比原始叶型大.因此优化后叶型在0～0.8轴向弦长处表面压差减小，有利于二次流损失的降低；0.8～0.9弦长处，原始叶型吸力面发生较为剧烈的扩压，而优化叶型则出现了压力平缓区，优化叶型压力面上的压力比原始叶型略有增加；0.9～1轴向弦长处，优化叶型与原始叶型吸力面均出现了扩压，压力面上压力基本重合.由图可知，优化后叶片吸力面的压力系数曲线比较平缓，有利于叶片气动负荷的减小，提高汽轮机级效率.

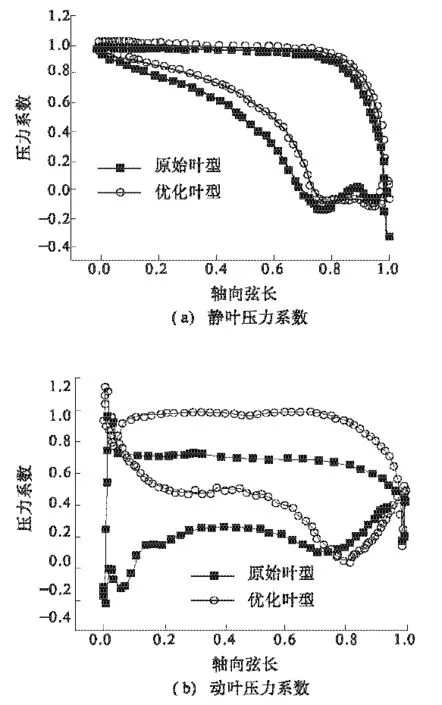
图3 叶片表面压力系数分布Fig.3 The pressure coefficient of blade

优化后动叶压力面的压力系数与原始叶片趋势相同，数值有所增加；吸力面上，原始叶片压力系数在0～0.45轴向弦长处基本处于扩压趋势，只在0.45～0.55弦长处平稳降低，然后又出现扩压现象；优化叶片吸力面上压力在0～0.8弦长处均呈下降趋势，转捩点由0.7推迟至0.8，减小扩压区区域，有利于减小叶型损失.

2.2 静叶表面压力分布

图4给出了优化前后静叶吸力面压力分布云图.从图中可以看出，优化后叶片表面的压力比原始叶型压力大；静叶中部压力降较原始叶型的小，有利于减小径向二次流损失.

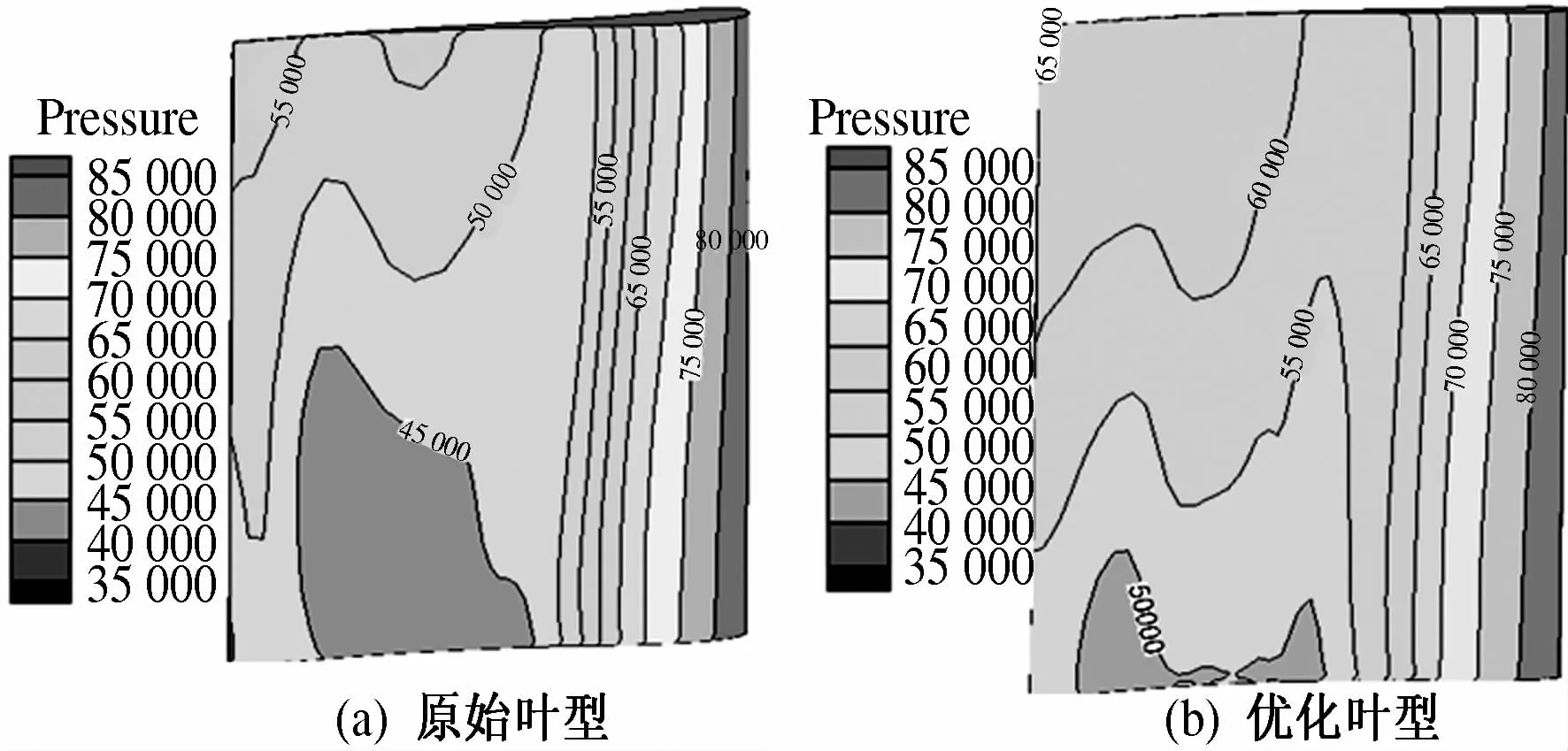
图4 静叶吸力面上压力分布图Fig.4 The pressure distribution in the suction of stator

2.3 叶片子午面速度分布

图5给出了优化前后叶片子午面上速度分布图.从图中可以看出，优化后叶片速度明显增大，大大增加了叶片的做功能力，且叶型优化后，动叶顶部出口截面上速度小于原始叶型，有利于叶片余速损失的降低.

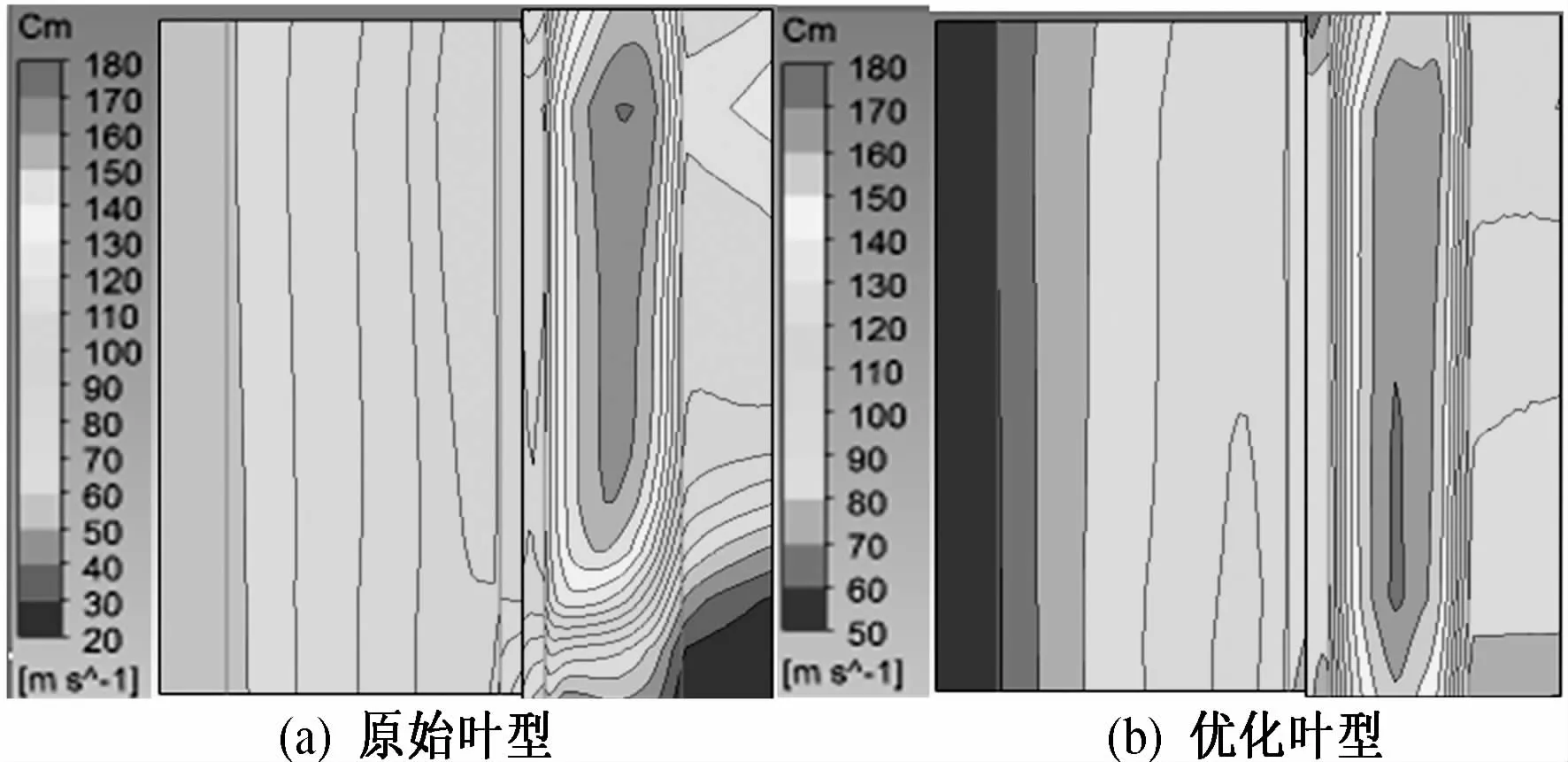
图5 叶片子午面上速度分布图Fig.5 Meridian velocity contours in meridian view

2.4 总压损失系数W

总压损失系数与汽轮机级内能量损失系数一一对应，因此可以采用W来表示叶栅的能量损失.定义表达式为

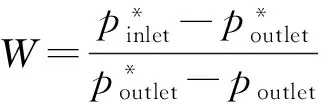
(5)

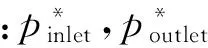
图6表示静叶栅总压损失系数沿叶高分布情况.从图中可以看出，叶栅总压损失沿叶高呈现增大趋势，优化后叶型总压损失在整个叶片范围处均比原始叶型小.在50%叶高处叶型总压损失系数由原来的6.5%降至5.5%，说明叶型优化后该级级内损失较小.

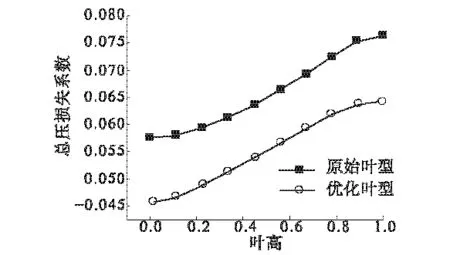
图6 静叶总压损失系数沿叶高分布曲线Fig.6 Total pressure loss coefficient in stator along span normalized

2.5 等熵效率ηi

等熵效率扣除了级内存在的所有能量损失，反应了级内蒸汽实际做功能力，即

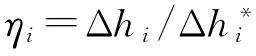
(6)

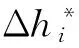
图7为沿流线方向等熵效率分布曲线.由图7可以看出，优化后静叶等熵效率基本与原始叶型一致，在0.8～1弦长处有所增加；等熵效率在动叶前缘处较低，说明损失主要发生在动叶前缘处，经过优化，动叶前缘处等熵效率较原始叶型有所增加，而在0.3～0.5动叶弦长处优化叶型较原始叶型等熵效率反而下降，之后又有增加，叶型优化后出口等熵效率由原来的92.099%提高至93.175%.

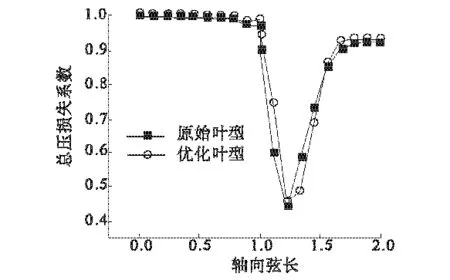
图7 沿流线方向等熵效率分布Fig.7 Distribution of isentropic efficiency along streamwise location

图8为等熵效率沿叶高分布曲线，从图中可以看出，静叶的等熵效率在叶根和叶顶处较低，说明在叶根和叶顶处叶栅损失较大.优化后叶型等熵效率只在叶根处较原始叶型低，但是在0.2～1叶高处等熵效率均有所增加.动叶等熵效率较静叶小，说明动叶中损失比较严重，叶型优化后等熵效率在叶根至0.4叶高处比原始叶型小，而在0.4至叶顶处比原始叶型处大，可以考虑采用变截面叶型来减小损失，提高叶型效率.图9为型线优化前后对比.

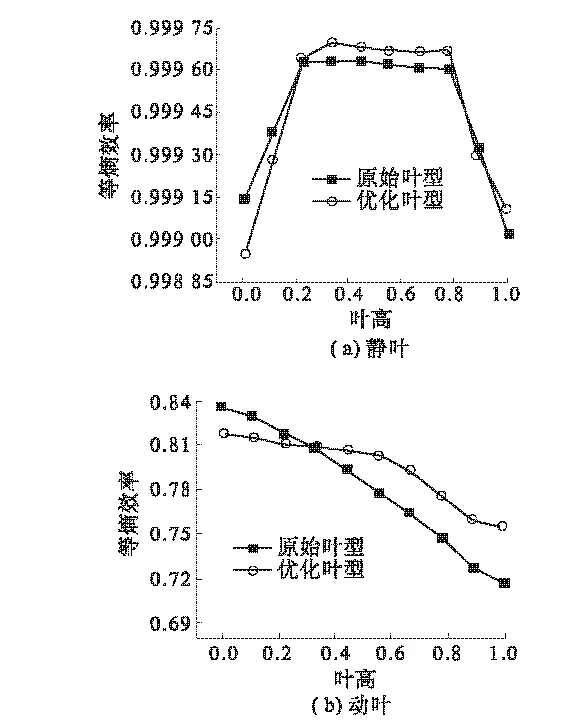
图8 等熵效率沿叶高分布曲线Fig.8 Distribution of isentropic efficiency along span normalized

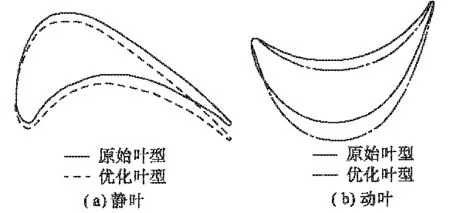
图9 优化前后型线Fig.9 Blade line before and after optimization

3 结论

(1)优化叶型压力面上的压力与原始叶型基本一致，而吸力面上压力比原始叶型大，但中部压力降较小；动叶区域速度明显增大，动叶顶部出口截面上速度略小于原始叶型，有利于降低叶片余速损失，增加叶片做功能力.

(2)静叶总压损失系数沿叶高逐渐增加，通过优化，静叶总压损失系数下降1%.

(3)静叶的等熵效率在叶根和叶顶处较低，优化后叶型等熵效率在叶根处较原始叶型低，但是在0.2～1叶高处均增加.动叶叶型优化后等熵效率在0～0.4叶高处比原始叶型小，而在此范围之外大于原始叶型.优化后级内等熵效率由原来的92.099%增加至93.157%.

[1] 雷风林.汽轮机末级变工况性能研究与流道改进设计[D] .郑州:郑州大学化工与能源学院,2010.

[2] WATANABE E, TANAKA Y, NAKANO T, et al. Development of new high efficiency steam turbine[J]. Mitsubishi Heavy Ind. Tech. Rev, 2003,40(4):1-6.

[3] 岳国强,李殿玺,韩万金,等.两套后部加载叶栅的对比实验研究[J].热能动力工程,2005, 20(2):125-129.

[4] 薛彦光.汽轮机级内二次流的数值模拟[D].吉林:东北电力大学能源与动力工程学院,2012.

[5] 崔海涛.汽轮机内部流场数值模拟及叶片改进优化[D].大连:大连理工大学能源与动力学院,2006.

[6] 王定标,雷风林,向飒,等.汽轮机末级变工况三维数值模拟与叶型改进设计[J].郑州大学学报:工学版,2010,31(5):1-4.

[7] 王福军.计算流体动力学分析[M].北京:清华大学出版社,2004.

[8] 陶文铨.数值传热学[M].西安:西安交通大学出版社, 2001.

Three-Dimensional Numerical Simulation and Optimization of Steam Turbine Blade

ZHOU Jun-jie, WANG Mei-ling, GUO Peng-fei, WANG Ding-biao

(School of Chemical Engineering & Energy, Zhengzhou University, Zhengzhou 450001, China)

The three-dimensional numerical simulation and optimization of the last stage of a 25 MW condensable steam turbine are conducted by using ANSYS Workbench, a platform of analysis system specially for the rotating machinery. The results show that the modified blade has a better pressure coefficient distribution, reduces the differential pressure distribution of blade surface, effectively controls the radial secondary flow losses. Total pressure loss coefficient is reduced, and the average total pressure loss coefficient is reduced by 1 %. Isentropic efficiency increases from 92.099 % to 93.157 %. After optimization, the aerodynamic performance of the blade increases obviously, the energy loss in the blade is reduced and the efficiency of steam turbine increases.

steam turbine; blade; aerodynamic performance; numerical simulation

2014-08-07；

2014-11-10

国家自然科学基金资助项目(51276173)

周俊杰(1974-)，男，河南太康人，郑州大学副教授，博士，主要研究方向为数值计算技术及其在过程设备中的应用，E-mail:zhoujj@zzu.edu.cn.

1671-6833(2015)01-0049-05

TK26

A

10.3969/j.issn.1671-6833.2015.01.012