聚类分析法在国际工程分包商选择中的应用

邱增健

（中国江苏国际经济技术合作集团有限公司，江苏 南京 210008）

0 引言

随着中国大量承包商涌进非洲工程承包市场，使得该地区的国际工程市场竞争越来越激烈，项目业主也对工程质量和承包商能力提出了更高要求。 现阶段，非洲地区国际工程市场的专业化程度越来越高，竞标愈加激烈，利润越来越低，中国承包商受到诸多因素的限制， 很难独立完成工程项目的所有施工任务， 需要对部分专项工程进行分包。 工程分包可以使中国承包商有效利用分包商的资源和优势来共同应对压力， 提高工程项目的完成效率和水平； 也能使中国承包商在一定程度上将部分项目风险进行转嫁。 因此，对非洲地区国际工程项目进行分包已成为中国承包商的必然选择。

如何选择优质、高效的分包商，已是中国承包商能否成功实施工程项目的重要环节。 针对该问题，本文从对分包商能力要求的角度，构建分包商选择评价体系，采用聚类分析法对分包商进行选择评价，为分包商选择决策提供科学依据。

1 理论概述

聚类分析方法是数据挖掘领域一种常见且重要的统计算法。 其原理在于将一个大数据指标比作是一多维空间，每一指标比作是一维，根据每一样本的数量空间计算样本距离，进而根据样本空间距离的远近程度将所有样本归为不同的集合，即将特征相似的数据元素纳入同一个集合，将特征不相似的数据元素纳入不同集合， 而这些集合可进行“二次”计算，将小集合归纳成大集合，以此类推，最终可将所有样本合为一个集合。

1.1 样本点距离测算

对非洲地区国际工程分包商的选择，可比作假设有n 个分包商，每一分包商有m 项专家评分，所有分包商的评分结果可作如下表示：

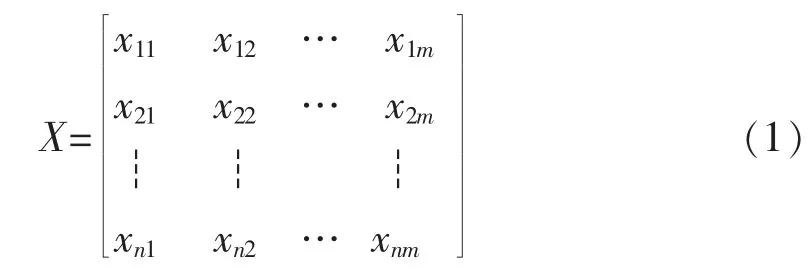
其中xij(i=1，…，n； j=I，…，m )为第i 个分包商第j 个指标的专家评分，任意两个分包商间的相似程度可用多维数量空间的两点距离来表示。明考斯基(Minkowski)距离是常用的距离公式：

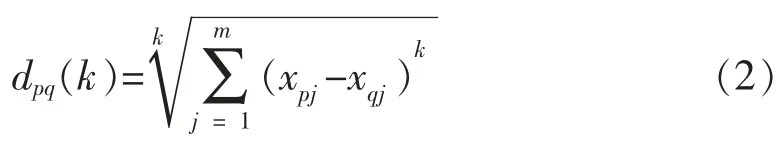
公式（2）中dpq表示点Xp与点Xq的明考斯基距离，一般而言，k 值取2，即欧式距离（见公式3），表示两个样本之间变量差值平方和的平方根。

1.2 分类集合距离测算

在分包商间距离测算的基础上， 还需将不同分包商进行分类，将分类集合间距离相近的归为一类。本文采用Ward 法测算集合与集合间的距离， 假设将n 个分包商分成z 个集合：G1, G2,… , Gz，用Xi(t)表示Gt 中的第i 个分包商，nt表示Gt中的分包商个数，X(t)是Gt的重心，则Gt中分包商的离差平方和为：

z 个集合的集合内离差平方和为：

由此可得，Ward 法的基本思路是使分类后同一集合的离差平方和较小，而集合与集合间的离差平方和应较大， 总的集合内离差平方和应相对最小， 即单一St内分包商的离差平方和应较小，St间的离差平方和应较大，S 的离差平方和应相对最小。

1.3 应用思路

基于以上原理知识，结合非洲地区国际工程分包商选择的流程特点，本文就应用聚类分析进行分包商选择提出以下步骤：

（1） 根据所有竞标分包商的专家评分结果，将所有指标的最高分汇总， 并假设其为最佳分包商，记为X0；同理，将所有指标的最低分汇总，并假设其为最差分包商，记为Xn+1。

（2） 将X0、Xn+1与所有竞标分包商的评分X1、X2、……、Xn根据以上原理进行聚类分析，若与最佳分包商同属一类的分包商数量满足决策的要求，则结束聚类分析；若数量仍过多，则进入第3 步。

（3） 将第2 步中与最差分包商属一类的分包商删除，同时，对应剩余的分包商各项指标评分，提高假设的最差分包商的各项指标得分。 此后，重复第2步结果，直至得到符合进行分包商决策的数量。

（4） 选取合适的分包商，对分包商进行选择决策。

2 实证应用

考虑到非洲地区的分包商日益增多，这在一定程度上增加了中国承包商对于分包商选择的工作量。因此，此选择评价过程，以分包商对应评价指标提交客观、公正、明确的自审材料为评价依据，进行匿名式专家评分。 根据专家评分结果，运用统计模型快速得出审核结果供抉择决策。 因此，本环节对模型的要求是便捷、快速、直观。 结合这一模型标准，本文以中国某承包商在非洲地区某国进行分包商招标选择为例，使用聚类分析法对分包商进行评价、选择。

2.1 构建指标评价体系

通过对该国分包商市场进行调研，结合具体工程实践，对分包商选择影响因素和能力要求进行分析，构建分包商选择评价指标体系，并根据各指标重要程度进行赋值，见表1。

表1 非洲地区国际工程分包商选择指标体系

经过公开招标后，共有9 家分包商对该分包工程进行了投标，通过对这9 家分包商依据表1 确定的指标进行筛选。

2.2 指标评分

根据表1，组建评审专家小组，评审专家由承包商内部专家和外部邀请专家共同组成，根据竞标的分包商资料，对分包商进行匿名评分。

2.3 分包商编号

各分包商的具体得分如表2 所示。 X1~X9为竞标分包商的得分矩阵，X0、X10为假设最佳与最差分包商的得分矩阵。

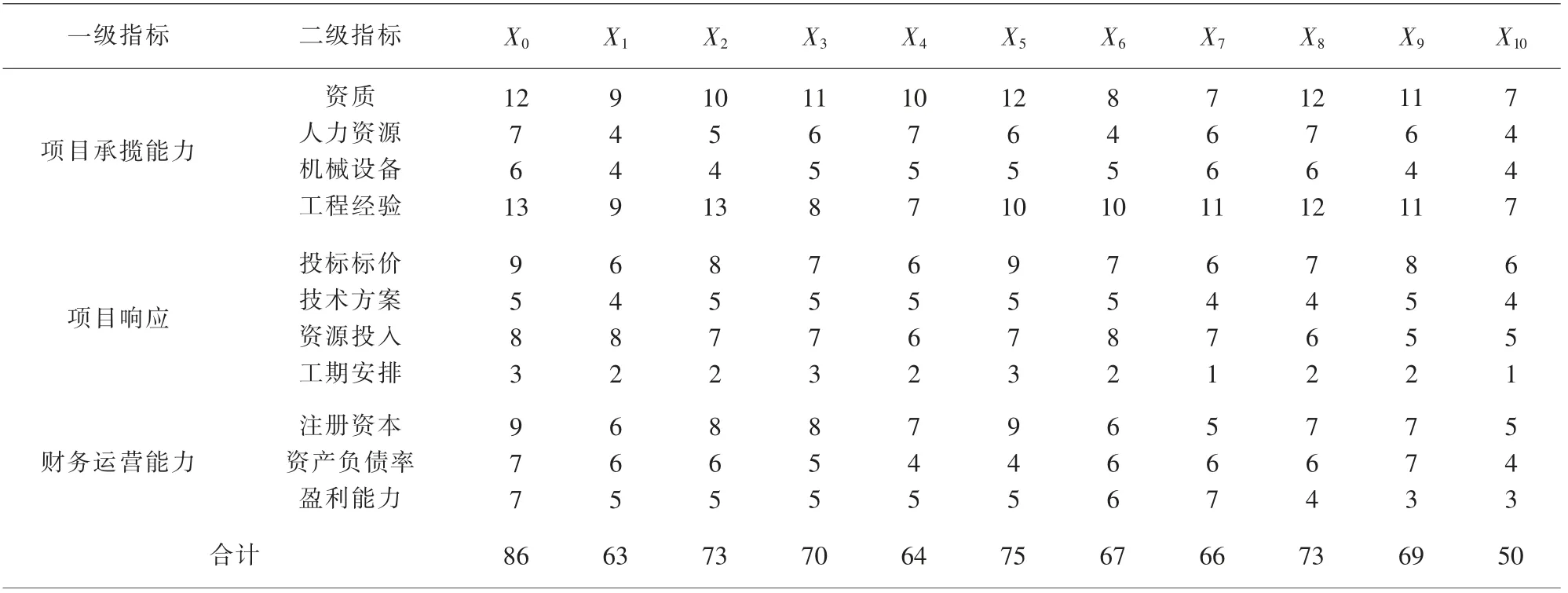
表2 第一阶段分包商指标得分

（1）第一阶段聚类分析

采用SPSS 21 统计分析软件对表2 中X0~X10的得分矩阵运用Ward 法进行系统聚类分析，分析结果如图1 所示。

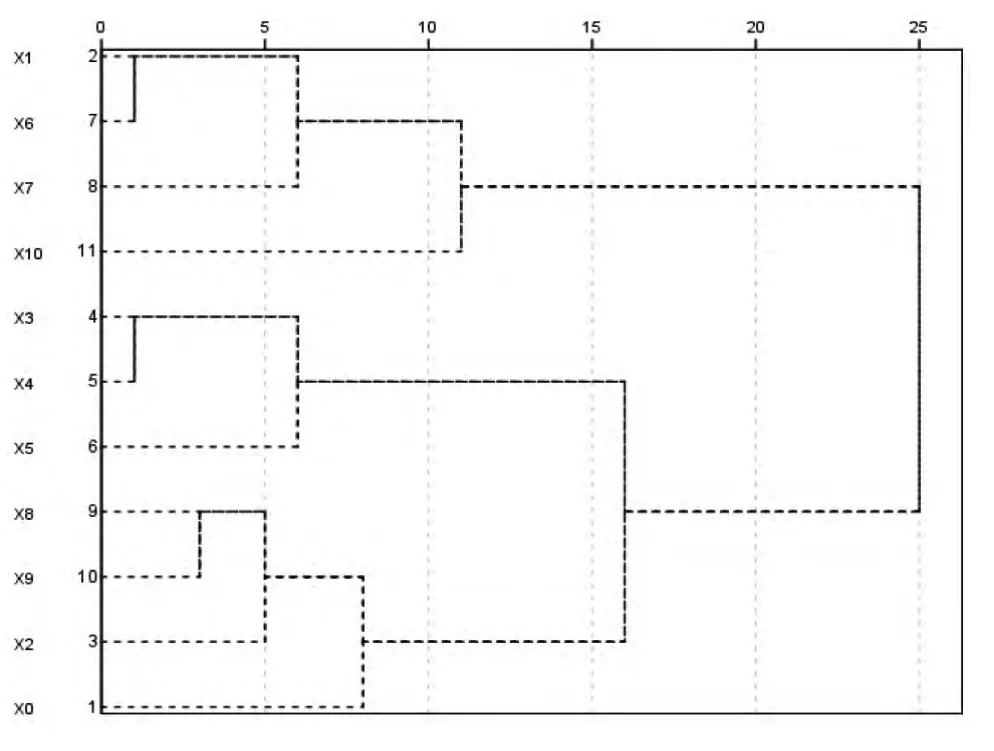
图1 第一阶段分包商聚类树形图分析

表3 第二阶段分包商指标得分

由图1 可得， 所有分包商分为了两类： ①X1、X6、X7等3 家分包商与最差分包商X10同属一类；②X3、X4、X5、X8、X9、X2等6 家分包商与最佳分包商X0同属一类。

（2）第二阶段聚类分析

由于第一阶段筛选后， 有6 家分包商满足条件，数目较多，因此进行第二阶段聚类分析。 删去X1、X6、X7这3 家分包商，同时，对应提高最差分包商各项指标的分值，见表3。 在此基础上，进行第二阶段的聚类分析，分析结果如图2 所示。

由图2 可得， 剩余的6 家分包商可分为两类：①X3、X4与最差分包商X10同属一类；X8、X9、X2、X5与最佳分包商X0同属一类。 因此，同理可删去X3、X4这两家分包商， 筛选出4 家分包商——X8、X9、X2、X5，进入下一轮的决策选择。

图2 第二阶段分包商聚类树形图分析

4 结语

基于聚类分析法的分包商选择，过程直观、结论简明，在工程实践中得到了广泛应用。 但该方法也存在较大不足，必须引起承包商的注意。

（1）当数据样本量较大时，可能难于获得聚类结论。

（2）应根据不同的选择目的选用不同的选择指标，一般而言，选择哪些指标应具备一定的理论支持，但在实践中往往是根据经验人为选择指标，使用不同的指标在不同的研究对象上具有明显差异。

（3）应注意数据量纲不同的问题，所有数据必须进行标准化。

[1]陈胜可.SPSS 统计分析从入门到精通（第二版）[M].北京：清华大学出版社,2013:300-313.

[2]马庆国.管理统计：数据获取、统计原理SPSS 工具与应用研究[M].北京：科学出版社,2010:156-161.