历史成本法与Excel函数在企业成本性态分析中的应用

□文/侍颖辉

（江苏省连云港工贸高等职业技术学校 江苏·连云港）

成本性态，就是指成本总额与业务总量之间的依存关系，通常又称为成本习性。成本性态分析是指在明确各种成本的性态的基础上，最终将企业的全部成本区分为固定成本和变动成本两大类，并建立相应的成本函数模型的过程。成本性态分析需要对混合成本进行分解，混合成本的分解就是运用一定的方法按成本性态将混合成本中的固定成本与变动成本部分区分出来。

一、总成本的函数模型

我们在分解混合成本之前，先要搞清楚成本按性态分类的总成本模型，总成本的数学模型可以用线性方程式y=a+bx表示。其中y是总成本，x是业务量，a是总成本中的固定成本，b是单位变动成本，bx代表变动成本总额。在这个直线方程中，业务量x是自变量，总成本y是因变量，固定成本a和单位变动成本b是常数，只要能确定a和b的值，由x值便能确定总成本y的值。混合成本的分解方法很多，有会计分析法、合同确认法、技术测定法、历史成本分析法，本文我们就着重介绍历史成本分析法及EXCEL函数分析法。

二、历史成本分析法常用的几种方法

历史成本分析法是根据混合成本在过去一定期间内的成本与业务量的历史资料，采用适当的数学方法对数据进行处理，从而分解出固定成本总额与单位变动成本的一种定量分析法。这种方法适用于生产条件较为稳定、成本水平波动不大以及有关历史资料比较完备的企业。

1、高低点法：就是指以某一时期的最高点产量的成本与最低点产量的成本之差，除以最高产量与最低产量之差，先计算出单位变动成本的值，然后再将混合成本中的变动部分和固定部分分解出来的一种方法。

根据方程式 y=a+bx和高点（x高，y高）、低点（x低，y低）可列出一组二元一次方程：

2、散布图法：是一种图解法，也称目测划线法或布点图法，它是在以横轴代表业务量，纵轴代表混合成本的坐标图中，将过去一定时期的业务量及成本数据分别在图中标出，形成散布图；然后根据目测在各点之间画一条反映成本随业务量变动的变动趋势的直线，以确定混合成本中的固定成本和变动成本。这种方法通过目测确定的趋势直线直观方便、易于应用，但不严密、精确，我们在此不作介绍。

3、回归直线法：也称最小二乘法或回归分析法，是通过回归方程来确定成本直线，用以分解混合成本的方法。主要原理是根据若干期产量和成本的历史资料，运用最小二乘法公式，将某项混合成本分解为变动成本和固定成本的方法。运用这种方法有一个前提条件，就是先确定x与y之间有无线性关系，如x与y相关性较强，则可分解；否则不必分解，分解出来无意义。相关系数r的计算公式：

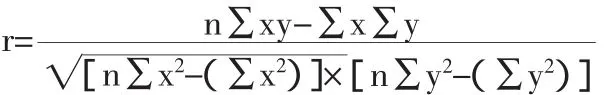
表1

表2

r绝对值大小说明x与y这两个变量的相关程度的密切程度，r=0说明变量之间不存在依存关系；r=±1说明变量完全相关，+1表示正相关，-1表示负相关。

Σyi=na+bΣxiΣxiyi＝aΣxi+bΣxi2

所以，代入化简得：

利用回归直线法进行混合成本分解，运用了“偏差平方和最小”的原理，所以结果更为精确，但计算过程比较复杂。

三、成本性态分析应用与设计

某企业2015年1～10月份的某项混合成本与产量的有关资料如表1所示。（表1）

1、采用高低点法。（表2）由表2数据知：

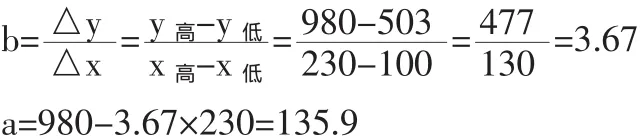
所以，混合成本的方程为：y=135.9+3.67x，高低点法简便易行，但它只选择了历史资料的高点和低点两组数据作为计算依据，代表性较差，结果不准确，建立起来的成本性态模型很可能不具代表性，这种方法只适用于成本变化趋势比较稳定的企业。为了更准确地反映成本性态模型，我们可采用回归直线法来建立。

图1

图2

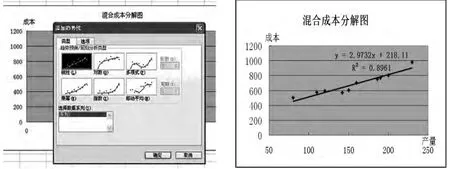
图3

2、采用回归直线法。先确定相关性，求相关系数：

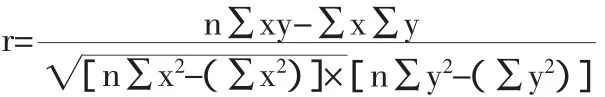
说明x与y之间具有比较密切的相关性，存在着线性关系，可用y=a+bx描述其变动趋势。

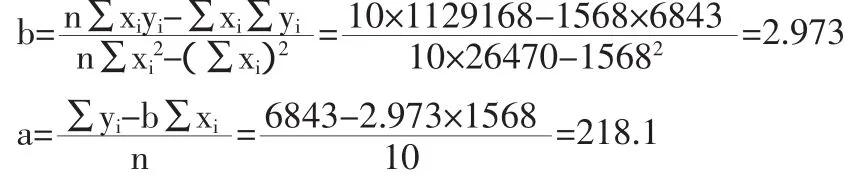
由上述数据求出如表3所示数据。（表3）进而求出：

代入相关系数公式得：

所以混合成本的方程为y=218.1+2.973x，明显较之高低点法有较高的准确性。但这种方法过于繁杂，计算量较大，稍有不慎就会出现错误，下面我们采用Excel的图表功能及相关函数可很快得到更为精确的数据。

3、Excel中intercept和slope函数在成本性态分析中的应用

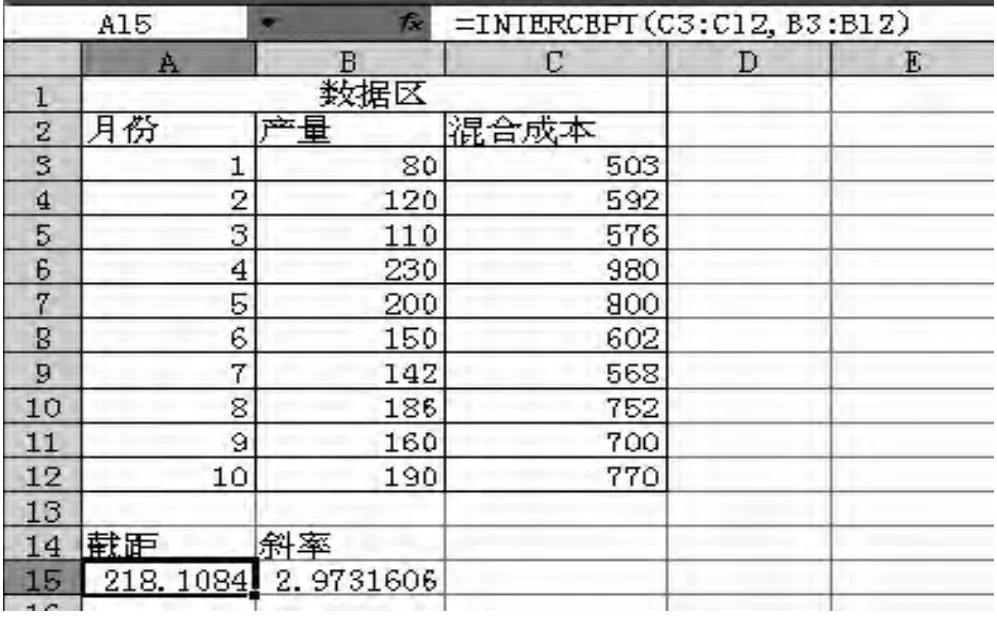
图4

图5

A、线性模型的建立

（1）在Excel数据表A1：C12中单元格中输入混合成本与产量的有关资料如图1所示。（图1）

（2）选择B3：C12数据，单击插入——图表——XY散点图，确定“系列产生在行”，输入图表标题“混合成本分解图”，数值X轴、Y轴为“产量”与“成本”，将图表“作为对象插入”，最终结果如图2所示。（图2）

（3）将鼠标移到散点图的数据点上——右击选择添加趋势线，选择类型为“线性”——在选项下勾选“显示公式”和“显示R2平方值”，在散点图上填加趋势线并显示公式和R2检验值，结果如图3所示。（图3）

（4）由上述的图3我们得知，混合成本的方程为y=218.11+2.9732x，相关系数的平方为0.8961，则相关系数r的值为0.9466。我们还可以用Intercept函数与Slope函数求出上述数据区的截距与斜率。在A15单元格中输入“=Intercept”即可得出截距为218.11，即为我们的固定成本；在B15单元格中输入“=Slope（C3∶C12，B3∶B12）”即可得出斜率为 2.9732.，即为我们的变动成本。结果如图4所示。（图4）

B、非线性模型的建立：从上图3中可以看出，点的分布并不是完全的线性状态，往往混合成本并非完全线性的，我们也不是一味拘泥于线性模型，可以根据情况利用非线性模型进行分解，从而得到更为精确的模型。

具体方法同上，建立如上图2的图形，将鼠标移到散点图的数据点上——右击选择添加趋势线，选择类型为“多项式”，设置“阶数为2”，如图5所示，在选项下勾选“显示公式”和“显示R2平方值”，在散点图上填加趋势线并显示公式和R2检验值，结果如图6所示。（图5、图6）

由图6我们知，r相关系数的平方为0.9561，所得r的值为0.9824，所以非线性模型较之线性有着更好的拟合性，相关程度更高，所以这时混合成本方程为y=0.018x2-2.6054x+615.85，这时其固定成本a为615.85，初始单位变动成本b为-2.6051。随着单位业务量的变化，单位变动成本的递增速率为0.036，较之线性模型更为准确。

在企业管理过程中，不仅要发挥相应的财务职能，还要根据企业自身情况对其生产经营决策提供依据，这就要求我们加强对企业成本性态的分析。以上几种方法是我们研究成本性态的常用方法，通过上述方法求混合成本可以发现：高低点法的优点在于简便易行，易于理解；缺点是由于它只选择了历史资料中的两组数据作为计算依据，使得建立起来的成本性态模型很可能不具有代表性，容易导致较大的计算误差。与高低点法相比，回归直线法由于选择了包括高低两点在内的全部观测数据，因而避免了高低点法中高低两点的选取带来的偶然性，比较科学，精确度高，但比较麻烦，计算复杂，公式不易记忆。EXCEL函数图表法，不但科学，精确度更高，操作简单方便。

［1］宗国恩.管理会计学.西南财经大学出版社，2012.1.

［2］ExcelHome.Excel2010实战技巧精粹，人民邮电出版社，2013.4.

［3］张亚红.完全成本法与变动成本法的比较及其结合应用.科技资讯导报，2007.11.