判定连续随机变量独立性的两个充要条件

2015-03-23王凡彬

大理大学学报 2015年6期

关键词：实数独立性学报

王凡彬

（1.内江师范学院数学与信息科学学院，四川内江 641100；2.四川省高等学校数值仿真重点实验室，四川内江 641100）

在多维随机变量 (X1,X2,…,Xn) 中，各分量X1,X2,…,Xn独立性的探讨目前主要还是按定义进行的，即按如下两个定义之一进行。

定义1 设n维随机变量(X1,X2,…,Xn)的联合分布函数为F(x1,x2,…,xn)，Fi(xi)为Xi的边际分布函数〔1〕。如果对任意n个实数x1,x2,…,xn，有

则称X1,X2,…,Xn相互独立。

定义2 设(X1,X2,…,Xn)为n维连续随机变量，p(x1,x2,…,xn)为联合密度函数，pi(xi)为Xi的密度函数〔1〕，如果对任意n个实数x1,x2,…,xn，有

则称X1,X2,…,Xn相互独立。

按如上两个定义对实际问题中的随机变量的独立性进行判定是较为困难和麻烦的。目前，对n维随机变量(X1,X2,…,Xn)各分量独立性的判定有一些研究〔2-10〕，但成果不多，或结果不够好，不能用两种方法进行处理。本文通过研究，得到了一个判定连续随机变量独立性的两个充要条件，使得该问题的处理变得容易，提高了工作效率。

1 独立性的判定

以下以二维连续随机变量(X,Y)中X,Y的独立性的判定讨论为主，更高维情形的研究是类似的。

首先，从(X,Y)的联合密度函数方面考虑，得到如下定理1。

定理1 设二维连续随机变量(X,Y)的联合密度函数为p(x,y)，(x,y)∈D，D为 R2中的区域；其余，p(x,y)=0。则X,Y相互独立的充要条件是：

（1）p(x,y)=φ(x)ψ(y)，

（2）D=(a,b)×(c,d)，

其中φ(x),ψ(y)分别为(a,b),(c,d)上的可积函数；a,b,c,d为实数，a,c可为-∞，b,d可为+∞。

证明：（充分性）按条件（1）、（2），X的边际密度函数

其余，pX(x)=0。

Y的边际密度函数为

其余，pY(y)=0。则

其余，pX(x)pY(y)=0。（3）式的成立用到了

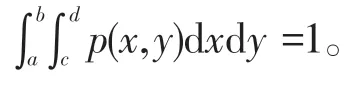
按独立性定义，X,Y相互独立。

（必要性）若X,Y相互独立，则

取pX(x)=φ(x),pY(y)=ψ(y)，则条件（1）成立；又X,Y相互独立，x,y的取值互相不影响，故D=(a,b)×(c,d)，即条件（2）成立。

注1：定理1 条件（1）中，分解式p(x,y)=φ(x)ψ(y)不具有唯一性。

其次，从(X,Y)的联合分布函数方面考虑，有下面的定理2。

定理2 设二维连续随机变量(X,Y)的联合分布函数为F(x,y)，(x,y)∈D，D为 R2中的区域；其余，F(x,y)=0。则X,Y相互独立的充要条件是：

（1）F(x,y)=f(x)g(y)，

（2）D=(a,b)×(c,d)，

其中f(x),g(y) 分别为(a,b),(c,d) 上的可导函数；a,b,c,d为实数，a,c可为-∞，b,d可为+∞。

证明：（充分性）当条件（1）、（2）成立时，(X,Y)的联合密度函数为

令φ(x)=f′(x),ψ(y)=g′(y)，则

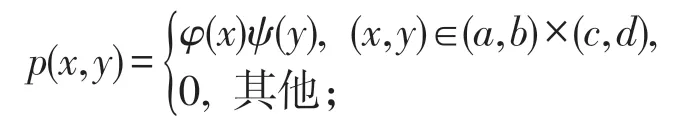
由定理1，X,Y相互独立。

（必要性）当X,Y相互独立时，有

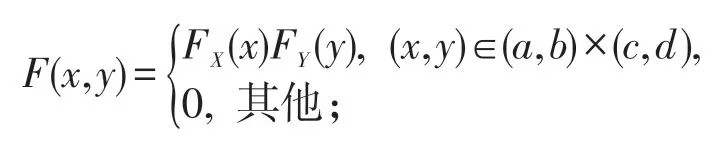
其中FX(x),FY(y)分别为X,Y的边际分布函数。令f(x)=FX(x),g(y)=FY(y) ，即知F(x,y)=f(x)g(y) ，(x,y)∈D= (a,b)×(c,d)，即定理 2 中的条件（1）、（2）成立。

注2：定理2 条件（1）中，分解式F(x,y)=f(x)g(y)不具有唯一性。

2 应用

定理1、定理2 的优点在于在实际问题的判断中，我们不必先由联合密度函数p(x,y)求出pX(x) ，pY(y)，然后再看是否有p(x,y)=pX(x)pY(y)；或不必先由联合分布函数F(x,y)求得FX(x),FY(y)，再验证是否有F(x,y)=FX(x)FY(y)，那样做将是比较麻烦的。而应用定理1、定理2，我们可直接观察p(x,y) 或F(x,y)的形态和D的形状，直接对p(x,y)或F(x,y)进行分解、判断，这就节省了时间和精力。下面试举两例，说明定理1、定理2 的应用，从中读者也可看到定理1、定理2的优点。

例1 设二维随机变量(X,Y)的联合密度函数如下，试问X与Y是否相互独立？