生态环境数据预测方法研究

罗桂兰，张 梅，冯立波，邓寿容，李 雨

（大理学院数学与计算机学院，云南大理 671003）

在全球气候变化条件下对云南生态环境变化趋势研究发现，温湿度对环境有着重大的影响〔1〕。温度升高，水资源短缺导致湖泊污染、森林退化和水土流失等加剧；降水以及温度的变化影响生物习性，同时导致雨季来临偏早，结束期也偏早的趋势。针对目前日趋恶化的生态环境，其保护显得越来越重要，生态环境监测所采集的大规模数据分析有助于环境现状评估和趋势预测。

实践证明时间序列分析方法中指数平滑法是一种性能优良、适应性强的数据分析方法，广泛应用于股票市场预测、旅游人数、物流分析等经济领域以及人口数量、交通流量等自然科学领域〔2〕。但针对生态环境的动态变化数据，指数平滑模型还有待改进。首先是平滑参数是静态的，难以随着时间的变化而变化，这样就大大降低了它对动态环境的适应性；其次是对参数的选择更多依赖于经验而难以达到最优值，参数预测效果的影响非常大，一般都要经过多次预测来选取最佳值，这样就极大地降低了预测效率；再次是平滑初值难以确定。为了提高模型的预测精度，本文基于二次指数平滑模型，将其静态参数动态化，并应用于动态生态环境数据行为分析，以找出数据的内在规律并预测其发展趋势〔3〕。

1 模型建立

设生态环境监测数据的时间序列为{xt} ，t=1,2,...,n，n为序列{xt} 原始数据的个数，xt是序列{xt} 的第t期实际值。则一次指数平滑模型为：

指数平滑法是一种确定性的平滑预测法，其实质是：通过计算指数平滑平均数来平滑时间序列，消除历史统计序列中的随机波动，以找出其主要发展趋势〔4〕。

以最小残差平方和为优化目标，即每一点x值的估计值和实际值xi之差的平方和θ，则

二次指数平滑法是对一次指数平滑的再平滑。它适用于具有线性趋势的时间序列。其模型为〔5〕

那么第t+m期预测值Ft+m为

其中aT为截距；bT为斜率，m为预测的超前期数且m≥1。

为使二次指数平滑模型能够适应时间序列自身的变化，变静态为动态，将（4）式展开得到

令

其中φt是关于时间t的函数，并且当t＞1 时，则0 ＜φt＜1 ，当t=1 时，有且约定初始状态值φt=1，得动态二次指数平滑模型为

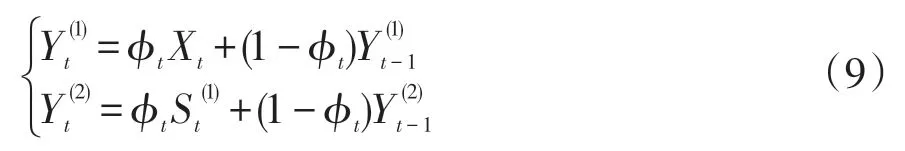
2 模型分析指标

2.1 可行性优化算法的可行性分析主要是比较θ和均方根误差η。θ用来表示随机误差的效应，一组数据的θ越小，其拟合程度越好。η用来衡量观测值同实际值之间的偏差，衡量一组数自身的离散程度，η越小越能够很好地反映出测量的精密度，公式为

2.2 相关性相关性用来表征两个因素之间存在一定的联系〔6〕。相关系数R用于研究温度W和湿度S之间是否存在某种依存关系，并对具体依存关系探讨其相关方向以及相关程度。而协方差cov(W,S)用于衡量两个变量的总体误差，序列W和S的相关性分析计算公式为

其中 ||R≥0.95 存在显著性相关；0.8 ≤ ||R＜0.95 高度相关；0.5 ≤ ||R＜0.8 中度相关；0.3 ≤ ||R＜0.5 低度相关； ||R＜0.3 关系极弱，若cov(W,S)=0，则称W和S不相关。

2.3 独立性独立性用来表征数据自身的特点〔7〕。方差β2是各个数据与平均数Xˉ之差的平方和的平均数，方差越大，说明数据的波动越大，越不稳定〔8〕，公式为

3 实验仿真与测试

3.1 实验仿真环境利用直接曲线拟合过程繁琐且精确度较低，本文借助Eviews 6.0，输入数据后可得到高度拟合曲线，所得数据精确，同时简化了数据处理过程，再用优化模型进行数据统计分析，使误差更小。

3.2 实验样本数据温湿度是环境监测中两个重要的物理量，其检测准确性严重影响系统的测量结果。本文借助项目开发设计的基于物联网生态环境监测节点进行实际数据采集，以云南省大理州洱海岸 2013 年 6 月 1 日至 2013 年 6 月 30 日温湿度采集数据样本（该样本已经过节点进行不合理性数据剔除与均值处理，所得数据均为处理后的实际均值）作为实验模拟数据，验证优化算法可行性，预测突发环境变化，寻找环境变化规律，并能根据规律预测环境变化趋势。

3.3 实验预设参数在指数平滑法中，预测成功的关键是恰当地选择α，参数设置得越优，预测结果越精确〔9〕。α值是根据时间序列的变化特性来选取的，它代表模型对时序变化的反应速度，又决定预测中修匀随机误差的能力。本文基于原来的静态参数α，分别用0.618 法、Fibonacci 法和二分法3 种典型一维搜索算法的综合对比选取最优α，做到具体问题具体分析以得到较好的预测值。见表1。

表1 优化参数选取值

在ERP项目实施工程中，发现利用θ作为预测精度评价指标更好〔10〕。运行结果显示：当温度优化参数αw=0.46 时，温度θw-min最小；当湿度优化参数αs=0.38时，湿度θs-min最小。

3.4 模型实现与预测由指数平滑公式，通过模型对温度和湿度数据的平滑处理结果见图1。

图1 温湿度初始值序列图

由此可见，温度数据波动趋势比湿度数据小，但温度与湿度的变化趋势呈一定相关性。

温湿度相关性分析见图2。

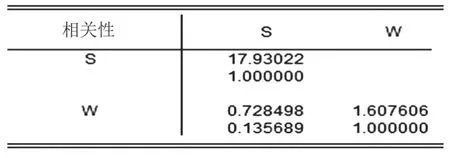
图2 温湿度相关性分析结果

图2中，温度方差β2=1.61，湿度方差β2=17.93，说明温度波动较小，湿度变化较大其值较不稳定；两序列相关系数R=0.14，cov(W,S)=0.73，由此可见温湿度有低度相关性，即温度对湿度值的影响较小。

温湿度静态二次平滑结果见图3。

图3 温湿度静态二次平滑序列图

由图3 可见，静态模型中二次指数比一次指数平滑曲线更趋近于实际值。但由于静态模型本身的局限性无法适应数据的动态变化，也无法获取二次指数平滑预测误差。为此基于动态模型分析得到如表2和表3所示预测结果。

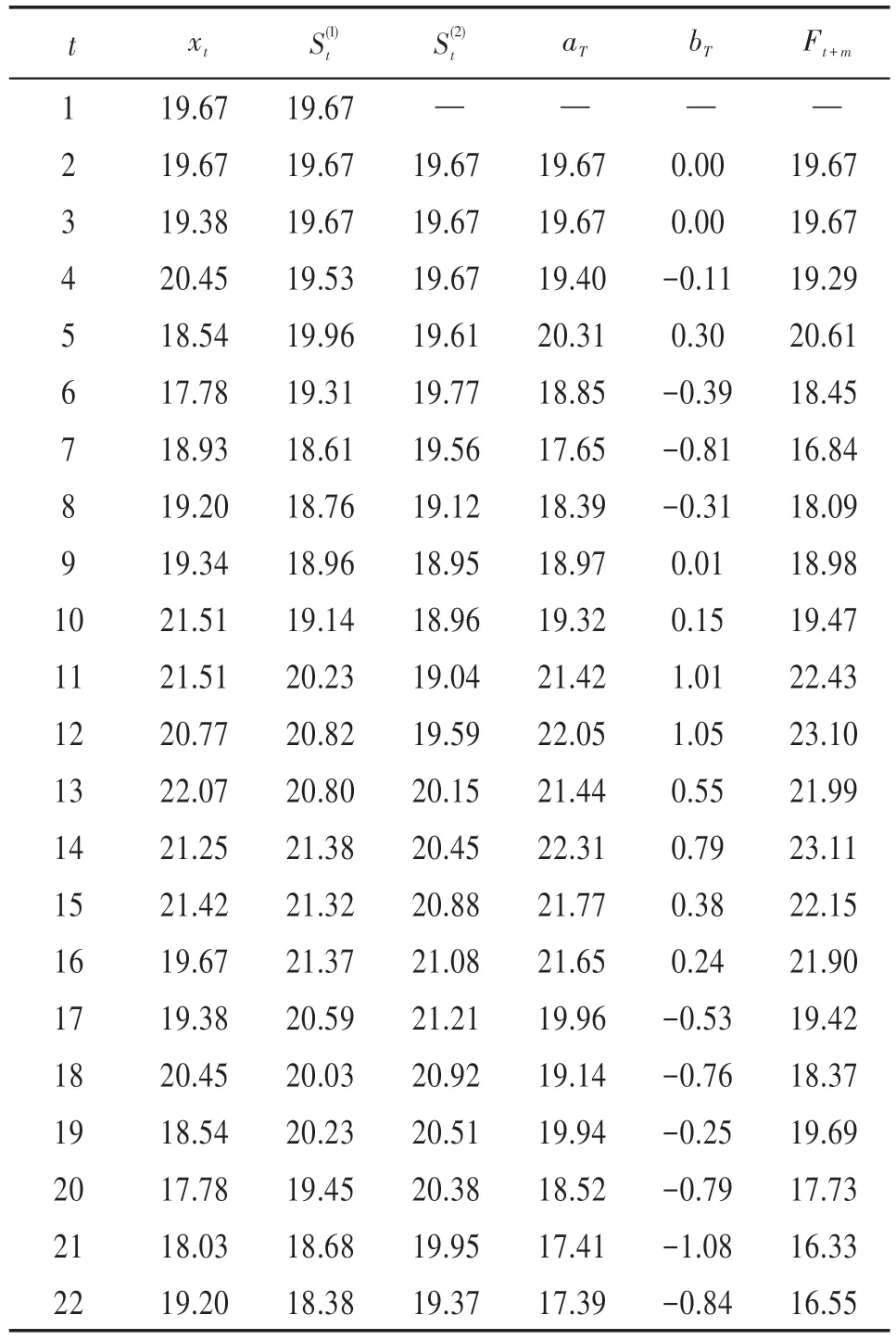
表2 温度动态模型预测数据

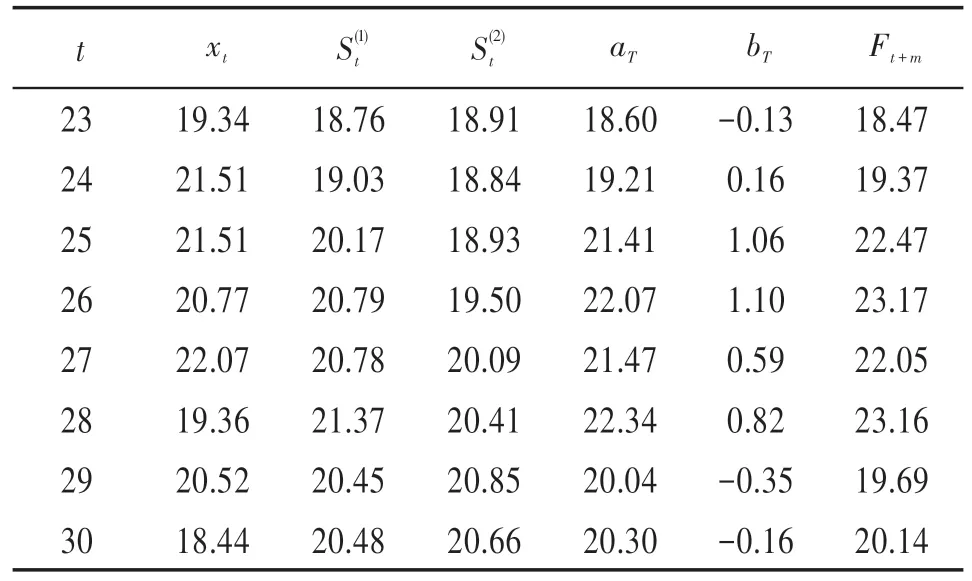
续表2

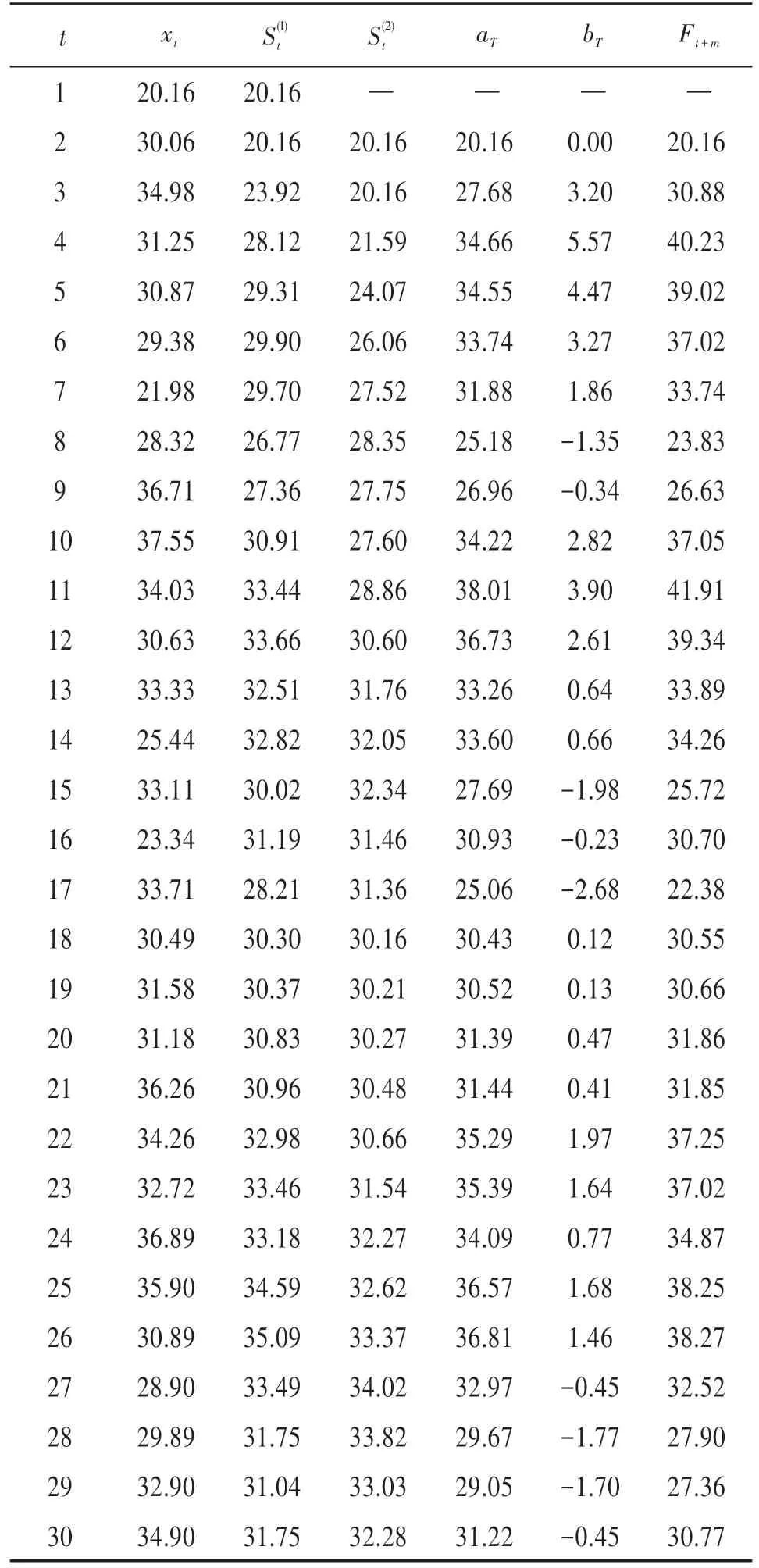
表3 湿度动态模型预测数据

那么相应温度二次指数平滑预测图见图4。

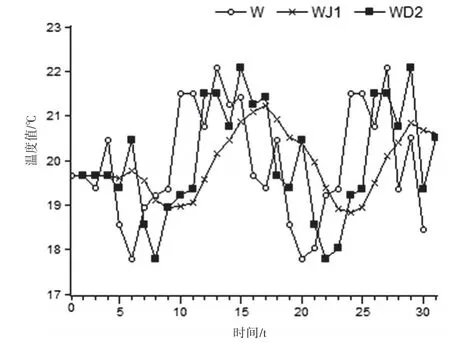
图4 温度二次指数平滑预测图

由图4 可见，改进后的动态二次指数平滑模型的拟合程度更贴近于温度实际值，明显优于原静态模型。

相应可得湿度二次指数平滑预测图见图5。

图5 湿度二次指数平滑预测图

温湿度静态模型与优化模型对比结果见表4、5。

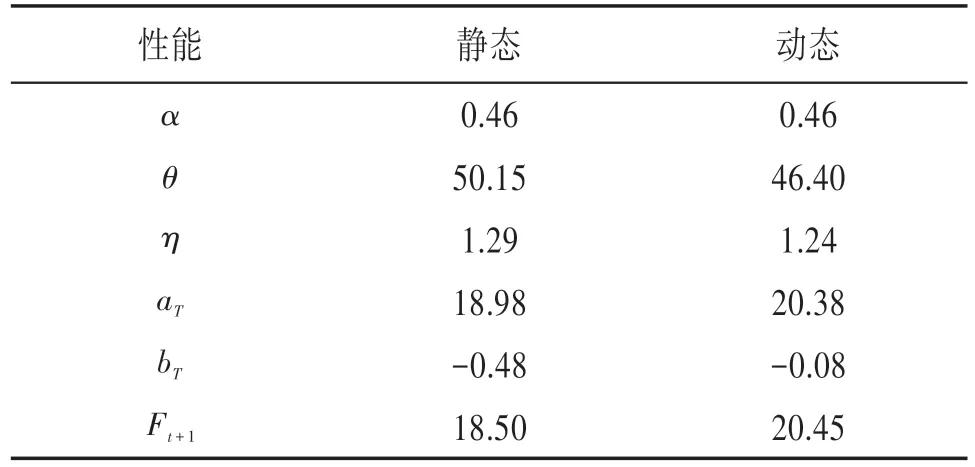
表4 温度动静态二次指数模型性能对比

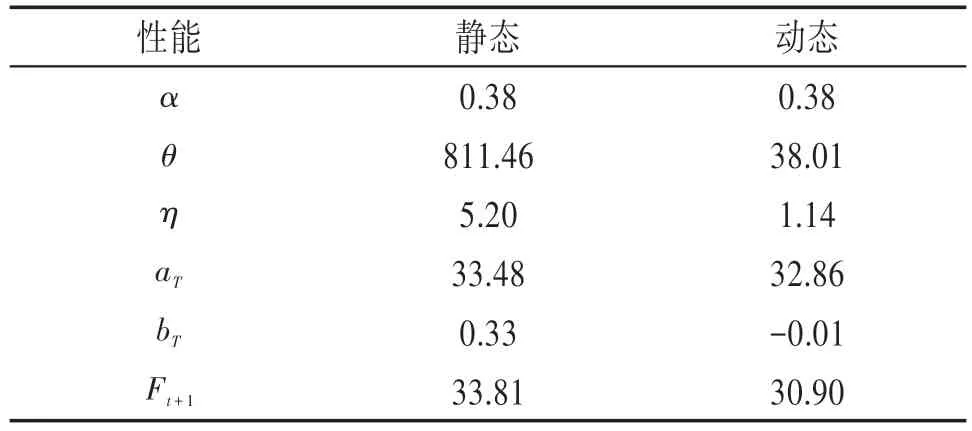
表5 湿度动静态二次指数模型性能对比

由表4 和表5 可见，当α=0.46 时，动态二次指数平滑模型得到的温度θ与η均小于静态模型所得结果，湿度亦是如此。由此可见，优化模型误差较小，具有普遍的适用性和可移植性。

4 结论

本文建立的动态二次指数平滑模型，主要是利用一维搜索算法得到动态最佳参数α，解决了静态参数难以随时间序列的变化而变化的问题。以最小θ为目标，通过温湿度两个实例分析，证实了改进的动态模型准确性优于静态模型，并在继承原有模型特点的基础上，有着自身的可适应性特点，实验证明，应用中短期预测误差较小，效果更好。

〔1〕李俊梅，樊林，段昌群.全球气候变化条件下云南生态环境变化趋势研究〔J〕.云南地理环境研究，2012 ，24（5）：67-73.

〔2〕杨金花. 基于改进预测模型的数据挖掘系统研究与实现〔D〕.成都：电子科技大学，2013.

〔3〕吴虎兵，夏志伟，陈剑铭.应用二次指数平滑模型预测及评价医院月平均住院日指标〔J〕.中国卫生信息管理杂志，2010，7（1）：71-73.

〔4〕周炳飞.动态三次指数平滑法及应用实例〔J〕.长春师范大学学报，2014，33（1）：10-13.

〔5〕蓝荣梅.基于指数平滑法的建设项目成本预测研究〔D〕.成都：西华大学，2013.

〔6〕张丽. 基于动态指数平滑模型的粮食价格预测方法研究〔D〕.郑州：河南工业大学，2011.

〔7〕杨政，原子霞.指数平滑转换的协整回归模型检验及其实证分析〔J〕. 数量经济技术经济研究，2010，11（6）：151-161.

〔8〕孙琦.基于协方差矩阵的目标跟踪方法〔D〕.哈尔滨：黑龙江大学，2012.

〔9〕何舒华，何霭琳.指数平滑法初始值计算与平滑系数选取的新方法〔J〕. 广州大学学报：自然科学版，2011，10（2）：6-10.

〔10〕孙东永，王义民，黄强，等.均方根误差最小准则的水库群典型年选取〔J〕. 西安理工大学学报，2011，27（3）：275-279.