LiF中空位形成能的第一性原理计算
2015-03-23何旭,杜泉
何 旭, 杜 泉
(1.成都纺织高等专科学校基础教学部, 成都 611731; 2.西华大学物理与化学学院, 成都 610039)
LiF中空位形成能的第一性原理计算
何 旭1, 杜 泉2
(1.成都纺织高等专科学校基础教学部, 成都 611731; 2.西华大学物理与化学学院, 成都 610039)
采用平面波展开和基于密度泛函理论框架下的第一性原理赝势法, 计算了102 GPa下LiF化合物中Li空位和F空位的形成能及空间周围的原子弛豫, 讨论了空位形成时电荷密度的重新分布, 相应的电子态密度以及能带结构等性质. 结果表明: LiF晶体中F空位的形成能比大于Li空位的形成能; F空位对LiF晶体的电子结构等性质的影响要比Li空位的大.
LiF; 高压; 空位形成能; 第一性原理计算
1 引 言
空位是晶体中最小也是最基本的缺陷形式,固体的许多物理性质都与空位的存在有着密切的关系. 详细研究空位形成和性质对理解材料的微观和宏观性能有着非常重要的意义[1].
LiF作为一种透光性很好的重要的窗口材料,其独特的物理和化学性质以及潜在的应用价值,引起了人们广泛的研究兴趣. LiF是一种典型的碱金属卤化物而且是碱金属氟化物中最难溶和最稳定的, 它对紫外线的透光率是所有物质中最高的[2]. 因此在光学材料中常用作紫外线的透明窗, 尤其是在冲击波实验中常常被用作光学窗口材料[3]. 实验研究表明: 窗口材料的光学透明性会随着压力的升高而减弱, 甚至丧失[4]. 理论研究[5]表明: 冲击诱导的点缺陷可能与其透明性降低现象有关. 但LiF单晶材料在160GPa的冲击压力范围内具有良好的高压透明性已得到公认[6-8]. 因此, 研究LiF在高压下的微观物质结构具有十分重要的物理意义.
目前, 用第一性原理和密度泛函B3LYP方法,研究晶体的空位结构是热门课题. 魏哲[9]等研究了含空位二维六角氮化硼的微观结构, 电子结构和磁性. 史海峰[10]等采用密度泛函理论研究了高压下单晶LiF的光学及热力学性质, 计算结果表明单晶氟化锂(LiF)在0~500 GPa静水压范围内具有良好的透明性, 计算所得晶格常数, 体积模量及其对压强的一阶导数与实验值较为符合.李海铭[11]等采用全势线性缀加平面波加局域轨道法, 研究了LiF的结构稳定性及电子和光学性质, 并得出LiF在53 GPa附近还存在一个结构相变. 何旭[12]等采用第一性原理研究了LiF含Li+1和F-1空位时的光学性质, 结果表明: 在紫外光波段,F空位比Li空位对LiF的光学透明性影响更大些. 徐梅[13]等采用密度泛函B3LYP方法研究了电场对LiF分子的能量及能级分布的影响等物理性质.
以上对单晶LiF的研究主要集中在理想晶体的电子结构及光学性质方面, 而利用第一性原理对单晶LiF中F空位和Li空位的形成能方面的研究尚未见报道. 本文采用平面波展开和第一性原理赝势法, 计算了LiF在102 GPa下理想晶体及Li空位和F空位存在时的体系总能量, Li和F两种空位点缺陷的形成能和空间周围的原子弛豫, 对比分析了Li空位和F空位存在时LiF晶体的能带结构, 电子态密度和电荷密度分布等性质. 这对解释LiF在高压下保持良好的光学透明性具有重要的理论参考价值.
2 理论模型和计算方法
LiF是立方体的NaCl型结构, 空间群为Fm3m, 利用第一性原理计算LiF晶体中的Li和F两种空位的形成能时, 首先建立LiF的原胞模型(见图1), 在此基础上扩展成含有32个原子格点的完整晶胞, 即含有16个Li和16个F格点, 然后在其立方体结构中去掉相应的Li或F原子, 再把该系统做周期性排列, 这样系统中所模拟的空位也是周期性排列的.研究单个空位的形成能时, 应尽量增大相邻空位间的距离, 达到使空位间的相互作用尽量小的目的.
本文的计算是基于局域密度泛函理论[14]的第一原理从头计算, 采用正则守恒的第一性原理赝势[15]和平面波展开晶体波函数, 并使用Ceperley-Alder等给出的交换关联公式[16]. 对缺陷形成能的第一性原理计算要求有两个方面: 一是电子态的自洽计算; 二是空位附近的离子需弛豫到各自的平衡位置[17]. 对于格点的弛豫进行了Hellmanner-Feynman力的计算,然后根据此力的大小调整格点的位置,再进行电子态的计算, 重复这个过程直到获得原胞中各原子的平衡位置. 首先求出优化后含空位晶胞的总体积及各原子的平衡位置, 然后计算出完整晶胞和去掉一个原子后含空位晶胞的总能量, 并将优化后的晶胞体积与实验结果进行了比对, 结果显示与实验值偏差很小,优化计算的精确度由下面的条件控制: 自洽收敛精度为2×10-5eV/atom,最大位移偏差为0.002 Å, 使用了布里渊区中3×3×6个K点进行迭代,再增大K点数, 总能量差小于0.001 eV. 计算能带结构时平面波截断能设置为300 eV; 原子间的相互作用收敛精度为0.05 eV/Å, 空带选取为48对于分别含Li和F空位晶体模型的设置方法及计算方法与理想晶体的相同.
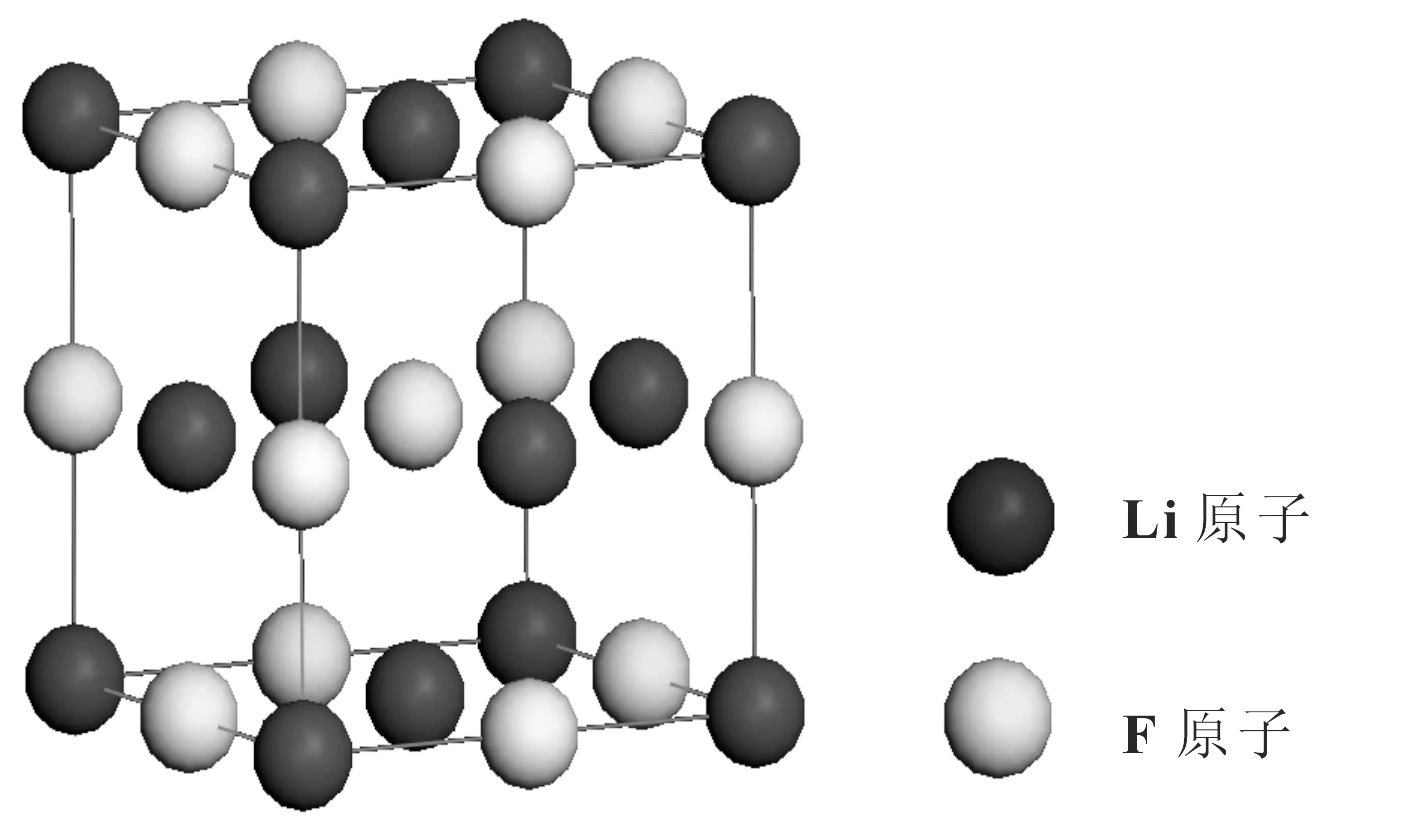
图1 LiF 理想晶体原胞模型 Fig.1 Ideal crystal cell model of LiF
为了说明计算结果的合理性,我们做了如下分析(见图2): (1)零压下LiF晶体的实验能隙值[18](14.2 eV)高于本文的计算值(9.52 eV). 应该说明的是, 这个明显的差别通常是由第一性原理计算理论的局限性造成的, 该理论更适合于预测基态的物性. 众所周知, 用第一性原理计算半导体和绝缘体材料的电子能隙时常常会导致低估结果, 这种偏低可以视为一种系统误差[19]. (2)虽然本文计算得到的LiF理想晶体的能隙随压力变化曲线整体上略高于文献[10]中计算得到的能隙随压力变化曲线, 但在这两条曲线中能隙随压力变化的趋势是一致的, 且在零压下本文计算的数值与实验值更接近. 我们认为本文给出的能隙随压力变化关系应该是合理的.
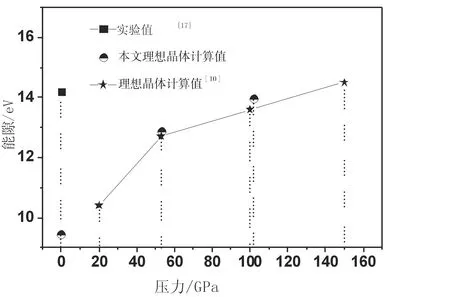
图2 LiF在不同压力下的能隙数据Fig.2 The energy gap data of LiF under different pressures
3 结果与讨论
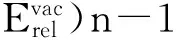

表1 LiF晶体的晶格常数、 体积、 总能量和空位形成能
为了更直观地理解原子间的键合作用性质, 还计算了LiF含32个格点的晶胞电荷密度分布情况. 图3给出了102 GPa下LiF超晶胞理想晶体及Li空位和F空位分存在下的电荷密度分布情况, 三个图中电荷密度分布图均沿LiF(NaCl型结构下)的100面. 由图3中(a)可以看出, Li原子与F原子之间的电子云密度重叠较弱, 这表明LiF晶体中Li-F之间形成的主要是离子键. 图3中的(b)和(c)与图3中(a)比较, 分别是中心偏左是少了一个Li原子及中间位置少了一个F原子, 从图(b)和(c)中可以看出: 形成Li空位时体系整体的电荷密度分布改变较小, 而当形成F空位时, 体系中的电荷密度分布有较大的改变, 这点与F独特的物理及化学性质分不开, F原子的电负性为4.0, 在已知元素中最大, 具有强烈的吸电子性, 在化合物中引入F原子后, 化合物分子内部的电子云密度分布会发生很大的改变[22].
图4给出了NaCl型结构的LiF在完整晶体、 含Li空位和F空位时的总电子态密度和能带结构图. 从态密度图可以看到, 形成Li 空位的情况对体系整体的态密度图像的影响是:价带宽度有所展宽, 总态密度的峰值有所增加, 并且在费米能级附近有缺陷态出现.但整体影响不大, 只是微扰而已. 而对于形成F空位的情况, 体系的电子态密度出现发生了很大的改变, 在价带上方大约6.47 eV的地方, 有明显的缺陷能级出现, 峰值及价带和导带带宽都有所变窄.

(a)

(b) (c)
Fig.3 The charge density distribution of LiF along the 100 surface(a)Li15F16(ideal crystal);(b)Li15F16(the center position is Li vacancy) ;(c)Li15F16(the center position is Li vacancy)
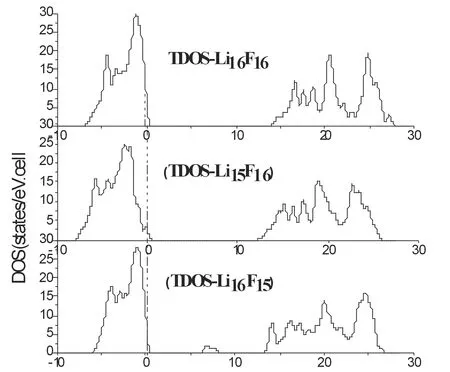
图4 LiF完整晶体,含Li空位以及含F空位时的电子态密度图(费米能级的位置已设为零点) Fig.4 Densities of electronic states of perfect crystal LiF, LiF including Li vacancy and F vacancy
表2给出了费米能级处的总电子态密度. 从表2可得: 102 GPa下LiF晶体中, F空位的总电子态密度是Li空位的总电子态密度的2倍多, F空位的产生, 较大地改变了费米能级的总电子态密度.
图5给出了NaCl型结构的LiF在完整晶体、 含Li空位和F空位时的能带结构图. 从能带结构图看: 当有Li空位存在时, 能隙值约为12.43 eV,比理想晶体的能隙值(Eg=13.97 eV)减小1.54 eV且在费米能级附近有缺陷能级出现; 当F空位存在时能带结构有较大的变化, 少一个F原子, 在费米能级上约6.49 eV的地方有缺陷能级出现, 对体系的性质产生较大的影响.

表2 LiF费米能级处的总电子态密度Table 2 The total electron density of states at Fermi level of LiF
4 结 论
使用平面波展开的第一性原理赝势法, 研究了窗口材料LiF晶体在最稳定的NaCl型结构下的Li空位以及含F空位的形成能, 讨论了相应情况的电子态密度, 能带结构和电荷密度分布情况等性质. 结果显示, Li空位的形成能要比F空位的形成能小很多; F空位的存在对LiF的电子结构及能带等性质的影响比Li空位的影响要大, 且两种空位的存在都引起了缺陷态的出现. 这些结论对解释LiF在高压下保持良好的光学透明性具有重要的理论参考价值.
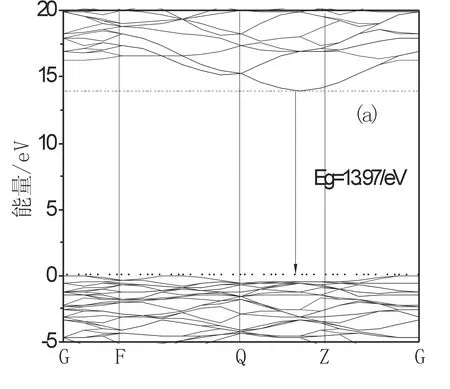
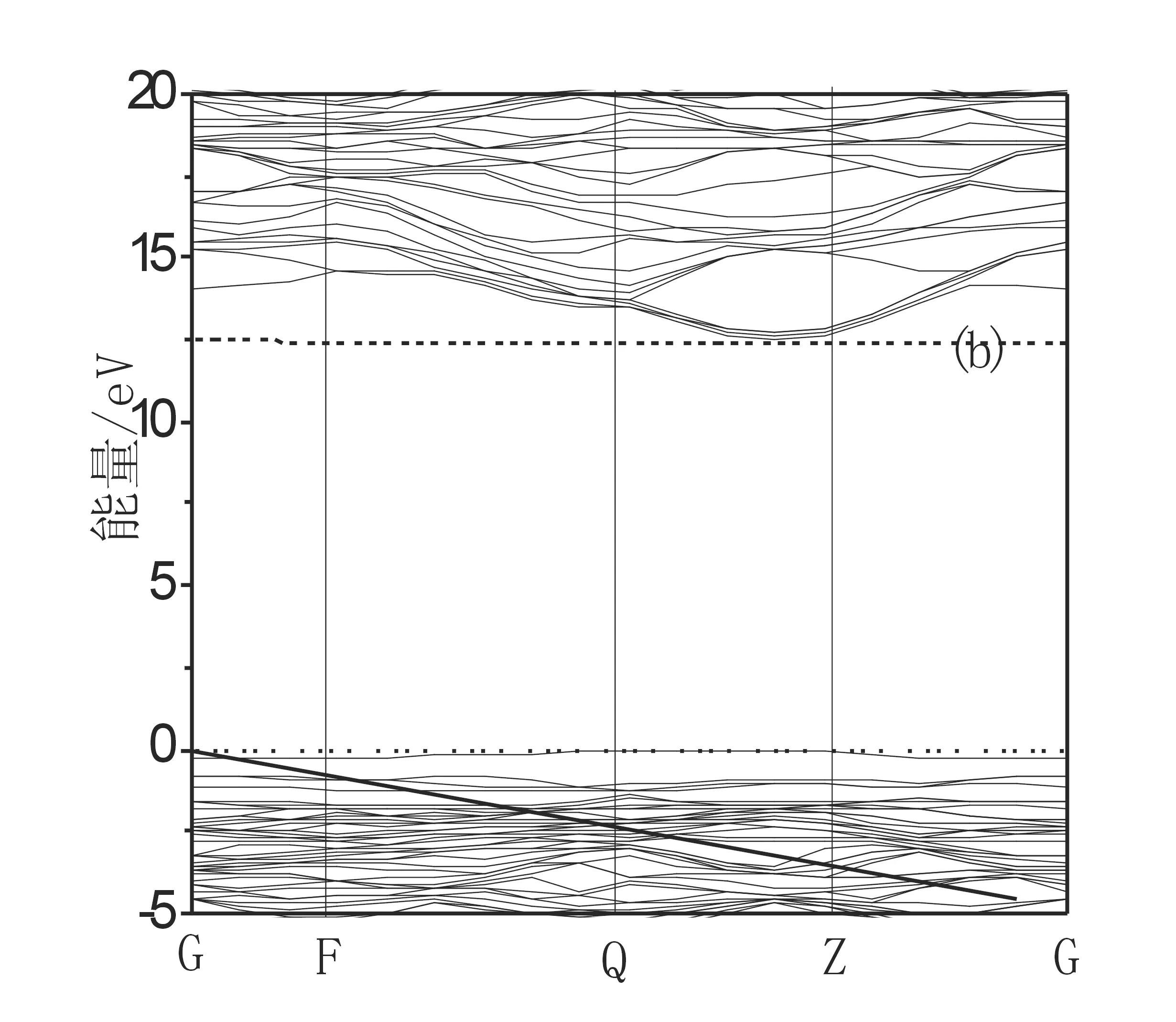
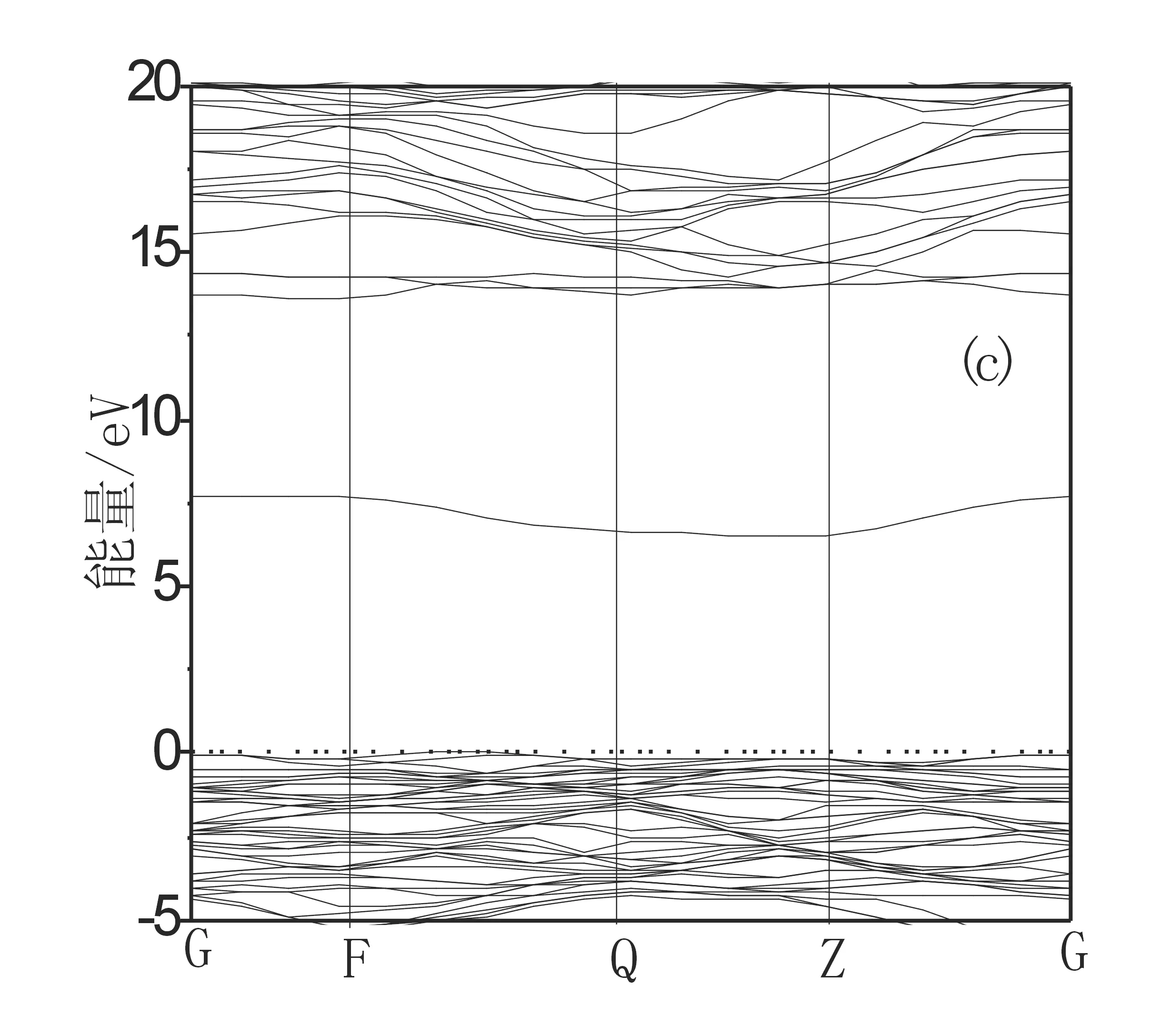
图5 102 GPa下LiF及分别含两种空位下的能带结构(a)理想晶体(b)含Li 空位 (c) 含F 空位
Fig.5 The band structure of perfect LiF and LiF containing the vacancy distinguish under the press of 102 GPa (a) Perfect crystal (b)LiF containing Li vacancy (c) LiF containing F vacancy
[1] Zhu J G, Zheng W S, Zheng J G,etal.Solidstatephysic[M]. 2nd ed. Beijing: Science Press, 2005 : 85 (in Chinese) [朱建国, 郑文琛, 郑家贵, 等. 固体物理[M]. 第2版.北京: 科学出版社, 2005: 85]
[2] Kin F M, Long J, Feng W,etal. Optical spectroscopy of graphene: From the far infrared to the ultraviolet [J].SolidStateCommunications, 2012, 152: 1341.
[3] Li J, Zhou X, Li J,etal. An optical absolute position measurement method using a phase-encoded single track binary code[J].ReviewofScientificInstruments, 2012, 5: 3902.
[4] Zhou X M, Wang X S, Li S N,etal. Under the strong shock compression LiF, Al2O3and LiTaO3single crystal pervious to light quality[J].ActaPhys.Sin., 2007, 56: 4965(in Chinese)[周显明, 汪小松, 李赛男, 等. 强冲击压缩下LiF, Al2O3和LiTaO3单晶的透光性[J]. 物理学报, 2007, 56: 4965]
[5] He L, Tang M J, Fang Y,etal. Origin of the change of the electrical and optical properties in shocked Al2O3and prediction of an increase in electrical conductivity in MgSiO3at pressure-temperature conditions of the Earth′s D′′ layer[J].EurophysLett., 2008, 83 : 39001.
[6] Wise J L, Chhabildas L C.Laserinterferometermeasurementsofrefractiveindexinshockcompxessedmaterials[M]. Shock waves in condensed matter, Springer D S, 1986: 441-454.
[7] Hicks D G, Celliers P M, Collins G W,etal. Equation of state of He-H2and He-D2dense fluid mixtures at high pressures and temperatures[J].Phys.Rev.Lett., 2003, 19: 35.
[8] Beobler R, Ross M, Boereker D B. Ideal quantum communication over noisy channels: a quantum optical implementation [J].Phys.Rev.Lett. 1997, 78: 45.
[9] Wei Z, Yuan J M, Li S H. Density functional study on the electronic and magnetic properties of two-dimensional hexagonal boron nitride containing vacancy[J].ActaPhys.Sin., 2013, 62 (20): 30 (in Chinese)[魏哲, 袁健美, 李顺辉, 等. 含空位二维六角氮化硼电子和磁性质的密度泛函研究[J]. 物理学报, 2013, 62(20): 30]
[10] Shi H F, Dai X F, Ji G F,etal. Ab initio simulations of optical and thermodynamic properties of LiF[J].J.At.Mol.Phys., 2006, 23 : 26 (in Chinese)[史海峰, 代雪峰, 姬广富, 等. 高压下单晶LiF的光学及热力学性质的密度泛函理论研究[J]. 原子与分子物理学报, 2006, 23: 26]
[11] Li H M, Wu X, Li J,etal. First principles investigation of structural stability and electronic and optical properties of LiF and NaF under high pressure[J].ActaPhys.Sin., 2007, 12: 32 (in Chinese)[李海铭, 巫翔, 李炯, 等. 高压下LiF和NaF的结构稳定性及其电子和光学性质的第一性原理研究[J]. 物理学报, 2007, 12: 32]
[12] He X, He L, Tang M J,etal. Effects of the vacancy point-defect on electronic structure and optical properties of LiF under high pressure: A first principles invest-ion[J].ActaPhys.Sin., 2011, 60 (02): 61 (in Chinese)[何旭, 何林, 唐明杰, 等. 第一性原理研究空位点缺陷对高压下LiF的电子结构和光学性质的影响[J]. 物理学报, 2011, 60(02): 61]
[13] Xu M, LingHu R F, Li Y F. Study on the physical properties of molecule LiF in external electric field[J].ActaPhys.Sin., 2012, 61: 93(in Chinese)[徐梅, 令狐荣锋, 李应发. LiF分子在外电场中的物理性质研究[J]. 物理学报, 2012, 61: 93]
[14] Kohn W, Sham L. Self-consistent equations including exchange and correlation effects[J].Phys.Rev. B, 1965, 140 : 11.
[15] Louie S G, Ho K M, Cohen M L. Self-consistent mixed-basis approach to the electronic structure of solids[J].Phys.Rev. B, 1979, 19: 17.
[16] Ceplerley D M, Alder B. Ground state of the electron gas by a stochastic method[J].Phys.Rev.Lett. 1980, 45: 50.
[17] Chen L J, Hou Z F, Zhu Z Z. First-principles calculation of the vacancy formati-on energies in LiAl[J].ActaPhys.Sin., 2003, 52 (09): 2229(in Chinese)[陈丽娟, 侯柱锋, 朱梓忠. LiAl中空位形成能的第一原理计算[J]. 物理学报, 2003, 52 (09): 2229]
[18] Piacentini M. A new interpretation of the fundamental exciton region in LiF[J].SolidStateCommun., 1975, 17: 65.
[19] Holm B, Ahuja R, Yourdshahyan Y,etal. Electronic and optical properties of γ-Al2O3from ab initio theory[J].Phys.Rev. B, 1999, 59: 12777.
[20] Wang X F, Yang J K, Huang D H. First-principles calculation of thermodynamic properties of LiF at high temperature and high pressure[J].JournalofMaterials, 2013, 10: 140(in Chinese)[王秀芳, 杨金科, 黄多辉. 高温高压下LiF热力学性质的第一性原理计算[J]. 材料导报, 2013, 10: 140]
[21] Ullrich H J, Uhlig A, Geise G,etal. Precise determination of the lattice constant of LiF by means of X-ray divergent beam (pseudo Kossel-) technique via computer graphics and multiple intersections[J].MicrochimicaActa, 1992, 10: 107.
[22] Zhang W, Xu J, Sun Z Q. Special functions and synthesis of aromatic fluorine-containing compounds[J].FineandSpecialtyChenicals, 2005, 5: 13(in Chinese)[张伟, 徐杰, 孙志强. 芳香族含氟化合物的特性及合成[J]. 精细与专用化学品, 2005, 5: 13]
First-principles calculation of the vacancy formation energies in LiF
HE Xu1, DU Quan2
(1. Department of Fundamental Courses, Chengdu Textile College, Chengdu 611731, China;2. School of Physics and Chemistry, Xihua University, Chengdu 610039, China)
We have employed the first-principles pseudopotentials and the plane wave energy band method to calculate the vacancy formation energies of F and Li vacancies in LiF intermetallic compound as well as the atomic relaxations around the vacancies. The charge redistribution around the vacancies and the electronic density of states are also discussed. The calculated results indicate that formation energy of F vacancy is bigger than that of Li vacancy in LiF crystal, and the effects on the electronic structure and other properties of LiF crystal due to F space are larger than those due to Li space.
LiF; Pressure; Vacancy formation energies; Frist-principles calculation
四川省教育厅重点项目(P09234)资助课题
何旭(1980—),女,硕士,助教,主要从事固体物质的高压特性研究. E-mail: hexu1225@126.com
杜泉.E-mail: duquanlm@163.com
103969/j.issn.1000-0364.2015.10.023
O469. 2
A
1000-0364(2015)05-0859-06
投稿日期:2014-06-06
