树木内部应力波传播速度模型
2015-03-23刘光林李光辉方益明
刘光林, 李光辉, 孙 晔, 方益明
树木内部应力波传播速度模型
刘光林1,2, 李光辉1,2, 孙 晔1,2, 方益明1,2
(1.浙江农林大学 信息工程学院,浙江 临安 311300;2.浙江农林大学 浙江省林业智能监测与信息技术研究重点实验室,浙江临安311300)
为了提高应力波技术在活立木无损检测应用领域的可行性,分析了应力波在健康树木中的传播规律,并建立了应力波传播速度数学模型。针对银杏Ginkgo biloba等不同树种的健康树木进行了多组实验,并利用树木断层成像技术对提出的应力波传播速度模型进行验证。结果表明:在健康树木中,方向角θ与传播方向速度vT和径向速度vR比值之间的关系为vT/vR≈-0.2θ2+1,与所提出的理论模型吻合,方向角θ与应力波传播速度之间的线性回归模型拟合度较高,决定系数高于0.95。提出的应力波传播速度模型不受树种变化影响。图6表3参12
木材科学与技术;应力波;速度模型;无损检测
应力波无损检测技术具有低成本,使用方便,不破坏被测木材,不受被测木材形状和尺寸影响等优点,已经在木材工业领域得到广泛研究和应用[1-2]。关于应力波传播理论,国际上也有了一些研究成果,但大多数是通过仿真或者试验分析证明传播模型的有效性[3-4]。国内也开展了相关研究,分析了应力波传播速度与树木的各种性能之间的相互关系,如王立海等[5]通过实验分析了木材截面的弦向角与应力波波速的关系,徐华东等[6]研究了温度和含水率对红松Pinus koraiensis木材中应力波传播速度的影响等。关于树木内部缺陷检测方面的研究也有很多报道,如Dikrallah等[7]通过导波实验分析了湿材的声学各向异性,研究了应力波速度与方向角之间的数学关系,梁善庆等[8]对多脂松Pinus resinosa进行检测,发现弹性波层析成像技术能够模拟出不规则树干形状并以二维图像方式直观地显示立木腐朽部位、程度、大小及形状等情况,Lin等[9]应用应力波断层影像技术评估樟树Cinnamomum camphora圆盘在不同大小的人造孔洞的影像反应来评估非破坏性因素与空洞大小的关系,冯海林等[10]依据各向同性和各向异性材料中的机械波传播理论,研究了应力波在木材中传播过程等。利用应力波检测树木内部缺陷还存在不少问题,如应力波在树木中传播理论研究尚未成熟;图像的重建问题还有待深入研究等[11]。笔者研究了7种树木方向角与树木横截面上应力波速度之间的变化规律,建立了应力波传播速度模型,并应用德国RINNTECH公司生产的Arbotom应力波木材无损检测仪对健康树木(活立木和原木)进行检测,对所提出的模型进行验证。
1 理论速度模型
将应力波传播速度方向与径向之间的夹角称为方向角。为了研究应力波在树木中的传播速度与方向角之间的关系,建立如图1所示的坐标系。图1中,S表示信号发射传感器所在位置,N表示接收传感器所在位置,SN表示传播方向T,θ表示它的方向角,且取值范围为θ∈(-π/2,π/2),当θ=0时,应力波沿径向传播。式(1)中:vT,vR,ER,ET,GRT分别代表沿T方向的传播速度、径向速度、径向弹性模量、切向弹性模量、剪切模量[8]。

图1 应力波在横截面传播平面坐标系Figure 1 Coordinate system of stress wave propagation on the cross section
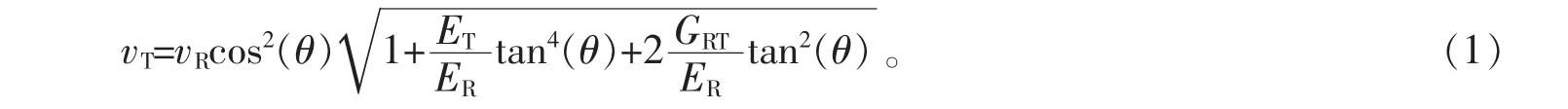

由式(2)可知:。当θ=0时,通过麦克劳林公式将方程展开为1个关于多项式和1个余项的和,代入化简得到如下方程:
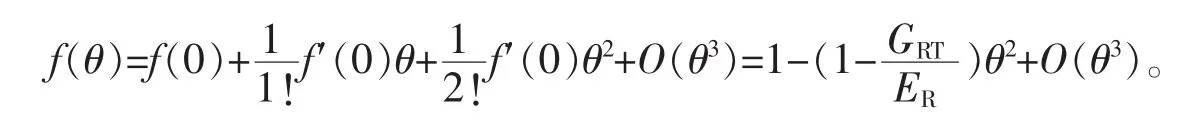
式(3)表明:在横截面近似为理想圆的情况下vT/vR与θ间的曲线近似为二次抛物线,且关于θ=0对称。本研究把式(3)作为健康树木中应力波在横截面上的传播速度模型。
2 材料、设备及方法
2.1 试验材料
在浙江农林大学植物园内,选取有代表性的健康活立木作为实验样本。具体为:樟树3株、银杏Ginkgo biloba 3株,鹅掌楸Liriodendron chinense 3株,柳杉Cryptomeria fortunei 3株,枫香Liquidambar formosana 1株,广玉兰Magnolia grandiflora 1株,重阳木Bischofia polycarpa 1株。另选取苦楝Melia azedarach,樟树,雪松Cedrus deodara等树种的健康圆盘作为原木试样,选择样本2个·树种-1,含水率范围分别为10%~12%,15%和24%~25%。
2.2 试验设备
本研究主要用到2种设备:①Arbotom应力波木材无损检测仪,用于测量应力波的传播时间,并对树木内部的健康状况进行断层成像检测,以便与提出的模型进行比较验证。②意大利KT-R打桩锤木材水分仪,用于快速测定试样的含水率。
2.3 试验内容和方法
对于活立木,分别在离地面40,80,120 cm等3个高度的横截面进行实验,如图2A所示。对于圆盘,分别在离上表面3.0和7.5 cm等2个横截面上进行实验,如图2B所示。

图2 检测位置Figure 2 Position of detection
实验在常温环境下进行,将Arbotom 12个传感器均匀地固定在试件周围,每个传感器用小锤轻敲3~5次,然后取平均值以控制误差。数据采集完成后,利用Microsoft Excel 2003和Origin 8软件进行数据分析与图形处理。为了直观显示样本内部的状态,还利用Arbotom应力波木材无损检测仪的二维成像软件,生成线段图和断层图像。
3 结果与分析
3.1 健康银杏树的平均速度模型
选取1个银杏样本,用Arbotom应力波木材无损检测仪在离地高度为80 cm处进行检测,生成的线段图和二维图,如图3所示。图3中,1,2,…,12分别表示12个传感器的位置。图3A中各传感器之间的直线表示应力波的传播路径,用颜色的深浅表示传播速度的大小,颜色越深表示传播速度越慢。一般情况下,健康木中的传播速度要大于非健康木。从图3A中可以看到绝大部分直线都是浅色的,说明传播速度较快,该样本是健康活立木。图3B是Arbotom应力波木材无损检测仪生成的断层图像,用浅灰色表示健康区域,深灰色表示腐朽区域。从图中也可看出,整个横截面都接近浅灰色,也说明选取的样本是健康活立木。
表1列出了各传感器间的应力波平均传播速度以及平均速度的比值(vT/vR)。表1中1,2,3,…,12分别表示12个传感器的序号,θ采用弧度制,即1°=π/180。从表1中可以发现,不同方向角的11组平均速度中,在R方向(θ=0)时应力波传播速度最大。
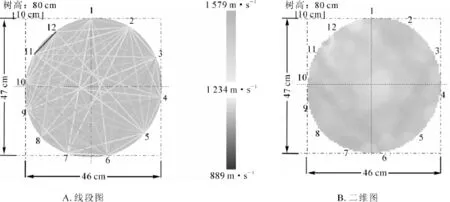
图3 健康银杏树的检测结果Figure 3 Test results of the healthy ginkgo tree
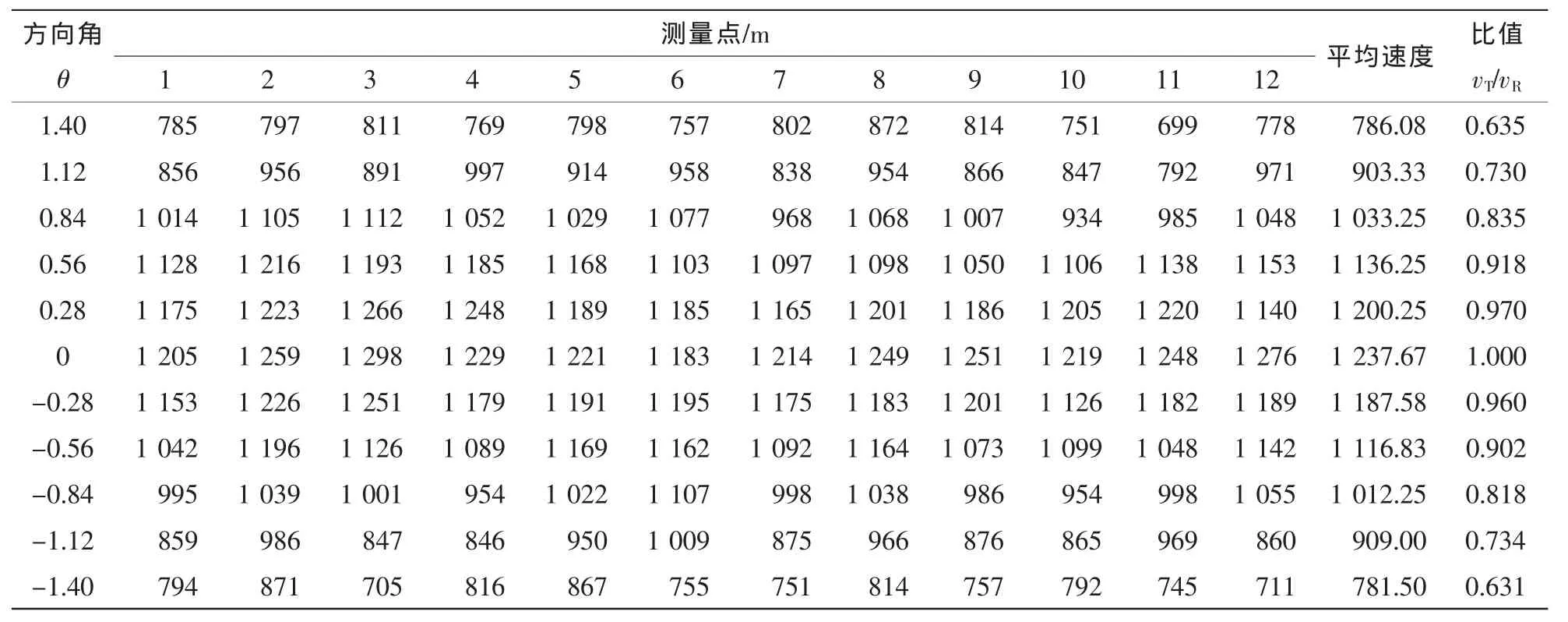
表1 高度80 cm处不同方向角应力波传播速度Table 1 Stress wave propagation velocity at the height 80 cm in different directional angles
应用Origin数据分析软件将表1中12个不同测量点每组θ与vT/vR的值进行拟合,结果如表2所示。从表2可知:在所建立的12个回归模型中,R2值均大于0.90,表明了模型具有较高的拟合优度,F检验置信度也都在0.001水平上,说明y与x之间具有很好的统计学意义。由此可知,二次项系数取标准误差波动较小的值,则A的取值范围约为―0.5≤A≤―0.2,由于θ的取值范围为-1.4~1.4,则一次项数值的大小对二次模型趋势变化基本无影响,所以B约等于0,而常数项C值约等于1。
将表1所得的数据应用Origin软件绘制得到应力波速度变化趋势图,如图4所示。该趋势线图由12条折线组成,每条折线上共有11个速度值,分别代表着每一个测量点11个不同方向角上的速度变化趋势。图中方向角采用弧度制,即1.40,1.12,…,-1.40依次代表角度75°,60°,…,-75°,趋势线图反映了12个传感器所有方向速度的变化规律。由图4知:传播速度随着方向角的减小呈先增后减的趋势,且最大值出现在传感器相对6的位置,即R方向,最小值出现在线图的两侧,即方向角为-75°和75°时,线图变化规律与表2中单个检测点的模型和理论速度模型所反映总体趋势是一样的。但具体到某一模型时,由于相关性程度还不是很高,使A值会在一定范围内波动,导致模型随机性较大。
为了解决单个检测点的速度模型随机性较大的问题,提高模型的拟合优度,减小单个点检测时速度误差,取平均速度作为实验分析的数据,从而控制实验误差。将表1中平均速度vT/vR的比值和θ进行拟合,所得的拟合方程称为平均速度模型,如图5所示,拟合方程为y=-0.180 9x2+0.003x+1,R2= 0.981,其中,y=vT/vR,x=θ。由此可知:平均速度模型能够反映高度为80 cm处银杏横截面上应力波传播速度变化规律,它比单个检测点的速度模型拟合优度更高,而且与理论分析的模型很好地吻合,说明理论速度模型是正确的。
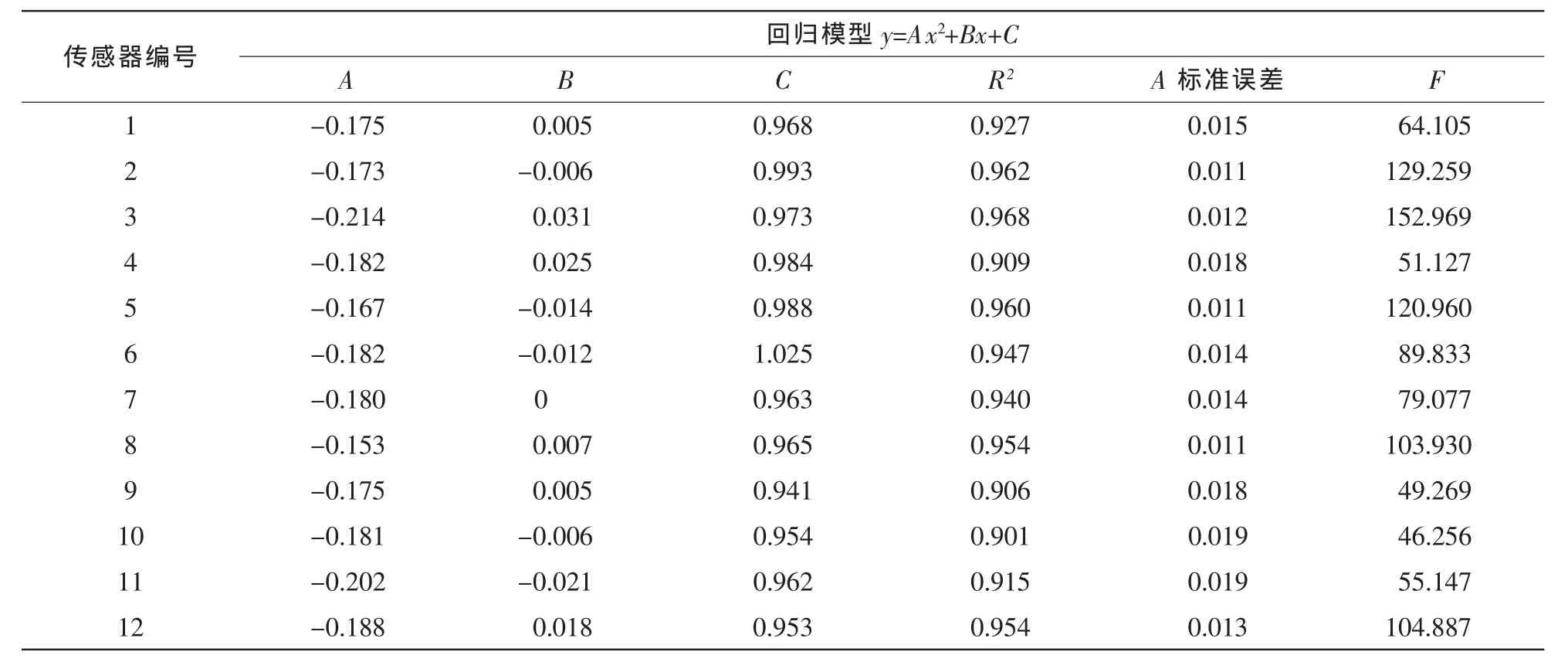
表2 每个传感器vT/vR与θ之间的一元二次回归模型Table 2 Quadratic regression model of the each sensor between vT/vRand θ
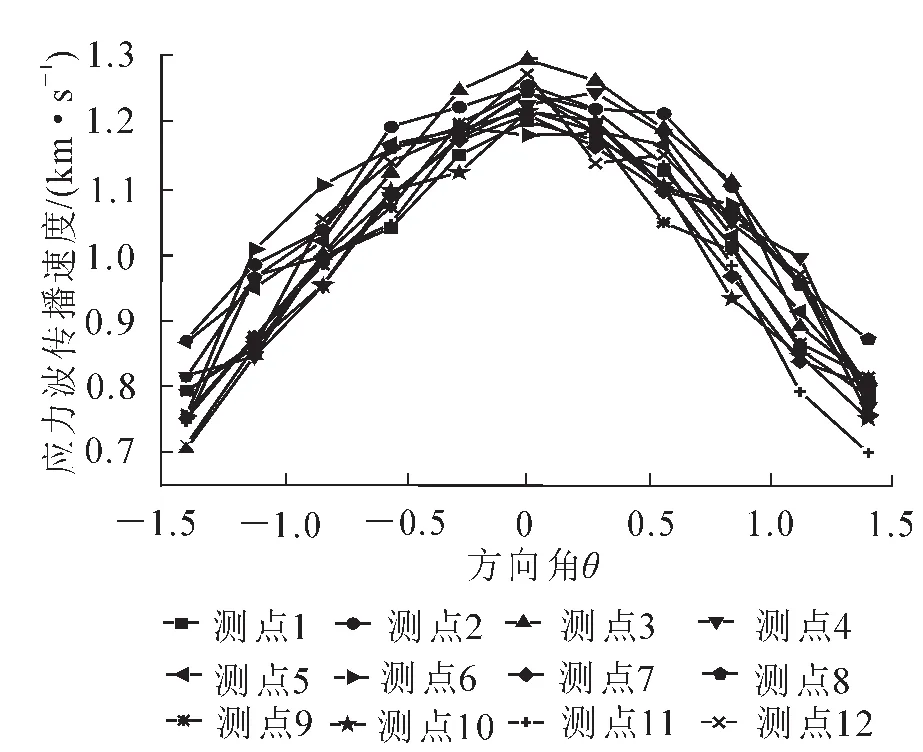
图4 应力波传播速度变化曲线Figure 4 Velocity trend lines of the stress wave
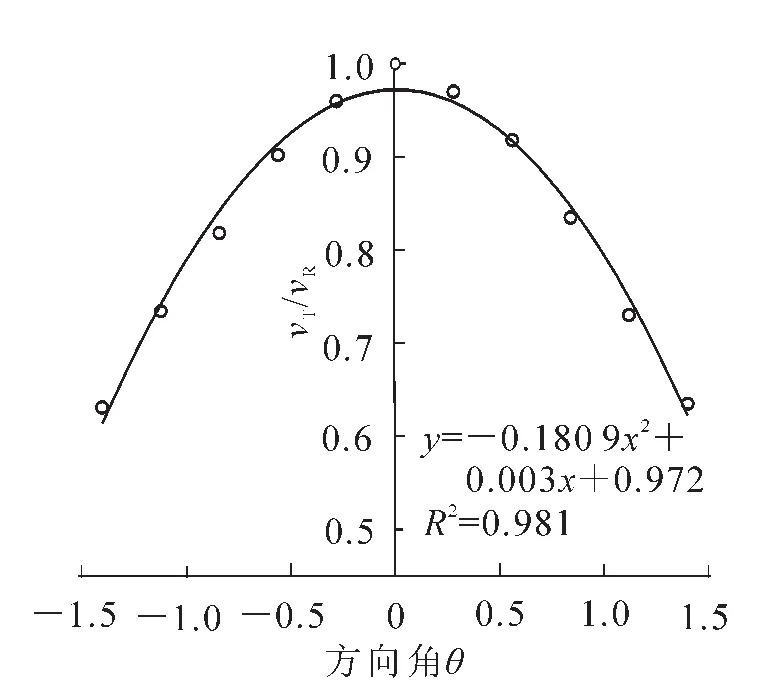
图5 平均速度模型曲线Figure 5 Curve of the average velocity pattern
3.2 不同树木的平均速度模型
采用与银杏相同的检测方法,分别对柏树(编号为1号)、鹅掌楸(编号为2号)、枫香(编号为3号)、柳杉(编号为4号)不同高度的横截面进行检测,实验获取的数据绘制不同高度应力波在树木内部横截面速度变化趋势线图,如图6所示。
从图6可知:在所检测的健康树木中,在不同树种中、不同横截面上应力波传播速度大小不同,但速度变化规律与银杏中的传播速度变化规律相同,传播速度都是随着θ的减小呈先增后减的趋势,最大值出现在径向,最小值出现在两端。木材属于各向异性材料,即使方向角相同,速度也不相同,它会在一定的范围内波动,因而单个检测点的速度模型不够理想,但速度总的变化趋势是一样的。
为了减小误差,选择与银杏相同的数据处理方法,将不同树木的y=vT/vR的值和θ进行拟合,所得数据如表3所示。由表3可知,拟合曲线满足一元二次方程,即y=Ax2+Bx+C,其中:A,B,C为常数。通过对多个横截面实验数据分析可知,A≈-0.2,B≈0,C≈1,且A,B,C的值与表2分析的结果相同。结果表明:平均速度模型能够很好地描述理论速度模型反映的速度变化规律,它们的图形都是开口向下的抛物线,且对称轴为θ=0,与单个检测点的模型相比平均速度模型相关性更高。因而实测数据能够验证所提出来的理论模型,表明了在不同健康树中具有相同的平均速度模型。

图6 不同树中速度变化趋势线Figure 6 Velocity trend lines of different trees

表3 不同树种中vT/vR与方向角θ之间关系Table 3 Relationship between vT/vRand θ in different tree species
4 结论
本研究分析了应力波在健康树木内部横截面上传播速度变化规律,并针对不同树种完成了实验研究。研究表明:在健康树木中,应力波传播速度随着方向角的减小(75°,60°,…,-75°)呈先增后减的趋势,当方向角为0时,方向速度最大,且方向速度和径向速度比值与方向角之间的关系符合一元二次方程:vT/vR≈-0.2θ2+1;与单个检测点的模型相比,平均速度模型和理论速度模型相关性更高,更能反映应力波在树木横截面上速度变化规律,因而它能够用来描述应力波在树木横截面上的传播速度变化规律;树种和检测位置的不同,会导致应力波传播速度的发生改变,但本研究所提出的应力波传播速度模型不受影响。木材属于各向异性材料,其内部结构相当复杂,此外,节子、腐朽、空洞等都会对应力波的传播产生影响[12]。因此,今后还需要在更多的样本上进行更深入的研究,提高模型的准确性。
[1] 管珣,赵茂程,王正.基于应力波技术测试木材材质的研究进展[J].林业机械与木工设备,2013(2):15-18. GUAN Xun,ZHAO Maocheng,WANG Zheng.Research progress in wood material testing based on stress wave technology[J].For Mach Woodwork Equ,2013(2):15-18.
[2] GUNTEKIN E,EMIROGLU Z G,YILMAZ T.Prediction of bending properties for turkish red pine(Pinus brutia Ten.)lumber using stress wave method[J].Bio Resour,2013,8(1):231-237.
[3] HAN Guangping,WU Qinglin,WANG Xiping.Stress-wave velocity of wood-based panels:effect of moisture,product type,and material direction[J].Forest Prod J,2006,56(1):28.
[4] TOMAR S K,KHURANA A.Elastic waves in an electro-microelastic solid[J].Inter J Solid&Struct,2008,45 (1):276-302.
[5] 王立海,王洋,徐华东.弦向角对应力波在原木横截面传播速度的影响[J].林业科学,2011,47(8):139-142. WANG Lihai,WANG Yang,XU Huadong.Effects of tangential angles on stress wave propagation velocities in log’s cross sections[J].Sci Silv Sin,2011,47(8):139-142.
[6] 徐华东,王立海.温度和含水率对红松木材中应力波传播速度的影响[J].林业科学,2011,47(9):123-128. XU Huadong,WANG Lihai.Effects of moisture content and temperature on propagation velocity of stress waves in korean pine wood[J].Sci Silv Sin,2011,47(9):123-128.
[7] DIKRALLAH A,HAKAM A, KABOUCHI B,et al.Experimental analysis of acoustic anisotropy of green wood by using guided waves[J].Proc ESWM-COST Action E,2006,35:149-154.
[8] 梁善庆,王喜平,蔡智勇,等.弹性波层析成像技术检测活立木腐朽[J].林业科学,2008,44(5):109-114. LIANG Shanqing,WANG Xiping,CAI Zhiyong,et al.Elastic ave tomography in standing tree decay detection [J].Sci Silv Sin,2008,44(5):109-114.
[9] LIN Chengjung,CHANG Tuntschu,JUAN Mingyang,et al.Stress wave tomography for the quantification of artificial hole detection in camphor trees(Cinnamomum camphora)[J].Taiwan J For Sci,2011,26(1):17-32.
[10] 冯海林,李光辉,方益明,等.应力波传播模型及其在木材检测中的应用[J].系统仿真学报,2010(6):1490 -1493. FENG Hailin,LI Guanghui,FANG Yiming,et al.Stress wave propagation modeling and application in wood testing[J].J Sys Simul,2010(6):1490-1493.
[11] 梁善庆.古树名木应力波断层成像诊断与评价技术研究[D].北京:中国林业科学研究院,2008. LIANG Shanqing.Study on Diagnosis and Assessment Technology of Stress Wave Tomography in Old and Famous Trees[D].Beijing:Chinese Academy of Forestry,2008.
[12] 林文树.应力波与超声波在木材内部缺陷检测中的对比研究[D].哈尔滨:东北林业大学,2005. LIN Wenshu.Comparing Studies between Stress-Wave and Ultrasonic in Inner Defect Wood[D].Harbin:Northeast Forestry University,2005.
A stress wave propagation velocity model of standing trees
LIU Guanglin1,2,LI Guanghui1,2,SUN Ye1,2,FANG Yiming1,2
(1.School of Information Engineering,Zhejiang A&F University,Lin’an 311300,Zhejiang,China;2.Zhejiang Provincial Key Laboratory of Intelligent Monitoring in Forestry and Information Technology,Zhejiang A&F University, Lin’an 311300,Zhejiang,China)
To improve the feasibility of nondestructive stress wave testing of standing trees,stress wave propagation in healthy trees was analyzed using linear regression analysis and a mathematical model of the stress wave propagation velocity was established.Several experiments were carried out for healthy trees of different species,and simultaneously the tomogram imaging technology was used to validate the proposed propagation velocity model of the stress wave.Experimental results of healthy trees showed that the linear regression relationship between the direction angle θ,the velocity (vT)for the propagation direction,and the radial velocity (vR)could be expressed as vT/vR≈-0.2 θ2+1,and the coefficient of determination R2>0.95,which demonstrated that the proposed mathematical model was correct.[Ch,6 fig.3 tab.12 ref.]
wood science and technology;stress wave;velocity model;nondestructive testing
S781.6
A
2095-0756(2015)01-0018-07
浙 江 农 林 大 学 学 报,2015,32(1):18-24
Journal of Zhejiang A&F University
10.11833/j.issn.2095-0756.2015.01.003
2014-02-26;
2014-05-14
国家自然科学基金资助项目(61272313,61302185,61472368);浙江省科学技术攻关项目(2012C21015,2013C31018,2013C24026);浙江省教育厅资助项目(Y201225450)
刘光林,从事木材无损检测技术研究。E-mail:liuguang1919@126.com。通信作者:李光辉,教授,博士,从事木材无损检测技术和无线传感器网络等研究。E-mail:lgh@zafu.edu.cn
