自然通风条件下催泪剂室内扩散特性的模拟研究

欧阳的华，张倩韬，赵 雁

（1. 武警工程大学装备工程学院，陕西 西安，710086；2. 陕西国际商贸学院，陕西 咸阳，712046）

目前，基于环境改善和污染控制的需要，国内外学者对空气或其他气体的室内扩散做了大量研究。如Paramasivam[1]研究了在自然通风时，窗口尺寸对室内环境的影响，确定了使室内处于热舒适情况下的通风口布置位置和窗口的长宽比。Yassin等人[2]则针对风速分布和大气污染物扩散之间的耦合统计关系，构建了相关的数学模型。国内，吴晋湘等[3]基于双尺度湍流模型对室内可燃气体泄漏进行了研究，并推导出了相应的经验公式；王晓华[4]采用数值模拟的方法，研究了可燃气体室内的扩散特性，蒋裕平等[5]则对甲醛的室内扩散特性进行了模拟研究；肖楚璠[6]研究了在自然通风条件下，室内家具所释放的甲醛的扩散特性。

武警部队在处置突发事件以及反恐作战过程中，根据战时特定情况需要，经常会向室内或者相对密闭的空间内（如机舱）投放催泪弹，以实现对恐怖分子的刺激作用。其作用效果的好坏则与催泪剂浓度的演变规律密切相关，而关于防暴弹催泪剂室内扩散特性研究的文献资料尚未见报道。因此，开展催泪剂在室内扩散特性的研究具有重要的现实意义。

为此，本文对催泪剂在室内自然通风条件下的扩散特性进行了研究，分析了室内不同观测点水平或竖直方向的催泪剂浓度，以期为今后催泪弹作用效能的评估和改进提供理论参考。

1 计算模型

1.1 数学模型

1.1.1 气相控制方程

假定催泪剂为均匀球体，在不考虑两相间的温度差、相变、颗粒物的形变及颗粒物间的相互作用时，其可视为二维定常不可压缩流动，对应的控制方程为：

（1）连续性方程：

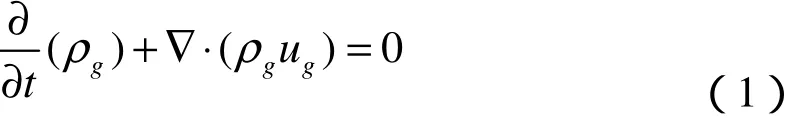
式（1）中：ug和ρg分别为气体的速度与密度。

（2）动量方程：

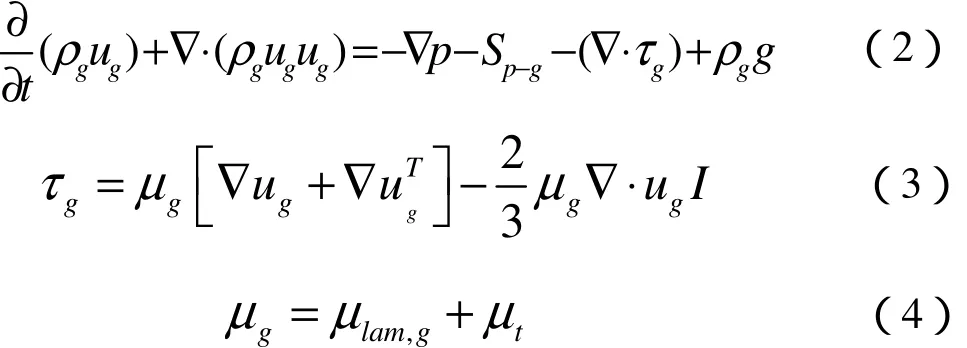
式（2）～（4）中：τg为气相应力张量；μg为气相粘度；μlam,g为气相层流动力粘度；μt为气相湍流动力粘度；I为单位矢量；Sp-g为两相间的作用力，其表达式为：

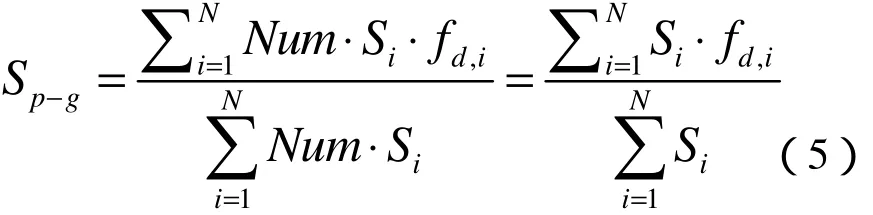
式（5）中：N为网格中催泪剂的数量；Num为单个模拟颗粒物所代表的真实催泪剂粒子数；Si为催泪剂粒子所在计算网格的球表面积。

1.1.2 运动学方程

计算时只考虑重力、萨夫曼（Saffman）升力和气体曳力的作用，依据牛顿第二定律，催泪剂的运动方程可表示为：

式（6）中：mi，ui分别表示催泪剂的质量和速度；g为重力加速度；FS为萨夫曼升力；FD为气体曳力。其中：

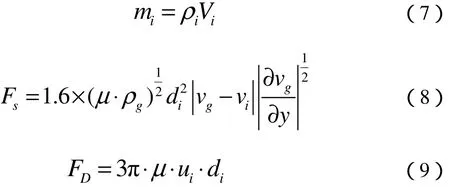
式（7）～（9）中：ρi，Vi，di分别为催泪剂的密度、体积和粒径；μ，ρg分别为空气的粘度系数和密度。

1.2 室内物理模型

首先构建房间的几何模型，如图1所示，房间长为5m（x轴方向），宽为4m（z轴方向），高为3 m（y轴方向）。房间左侧有一个门，右侧有一个可以开启的 1.6×1.6m2窗户。催泪弹的释放位置为点 s（x=1.55m，z=2.0m）。为了较好地观测不同位置的催泪剂浓度，计算时在垂直方向上选取了N1～N6共6个观测点，其对应的坐标位置分别为：N1（x=0.6m，z=0.6m），N2（x=0.6m，z=2.0m），N3（x=0.6m，z=3.4m），N4（x=2.5m，z=0.6m），N5（x=2.5m，z=2.0m），N6（x=2.5m，z=3.4m）；在水平方向上选取了N10～N12共 3个观测点，其对应的坐标位置分别为： N10（z=0.6m，y=1.1m），N11（z=2.0m，y=1.1m），N12（z=3.4m，y=1.1m）。

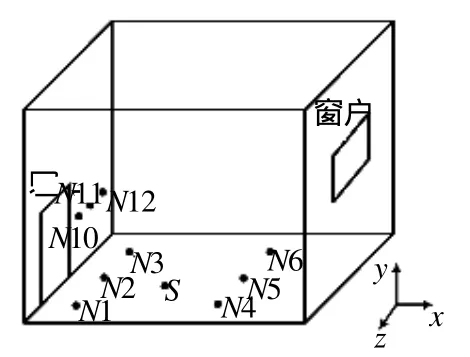
图1 室内模型示意图Fig.1 Schematic diagram of the interior model

室内的温度设定为常温（25℃），由于恐怖分子在室内时，门往往是紧闭的，所以可以不考虑室内通风，初始气流为静止流场，窗口为唯一的出口条件。催泪剂释放时的出口速度 ui,0=10m/s，催泪剂的直径为 10μm，密度为 1.3g/cm3。考虑到室内弹体释放源为单个弹体释放源，体积浓度计算起来相对较小，误差将增大，因此采用归一法的方法，将释放源处的催泪剂浓度设为1，其余位置浓度是相对释放源处的浓度大小。

1.3 物理及网格模型

如图 2（a）所示，先利用 CFD 前处理软件（Gambit）建立其三维模型，而后再采用结构化网格进行体网格划分，如图2（b）。根据文献[7]，网格特征尺寸（△s）应满足：

式（10）中λ为粒子间的平均自由程，其值在计算前通过估算获得。

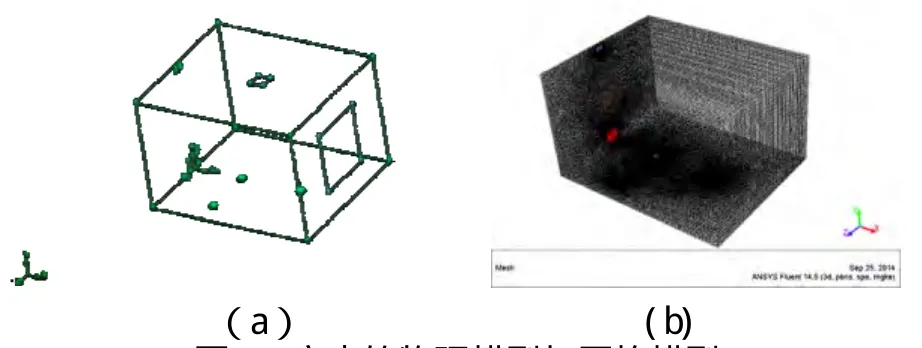
图2 室内的物理模型与网格模型Fig.2 Physical and mesh model of the interior

2 结果分析与讨论

2.1 流场及浓度分布

本文采用 FLUENT软件来求解各控制方程，通过有限体积法对各控制方程进行离散，压力与速度耦合采用 SIMPLE 算法，差分格式采用二阶迎风格式，以求得合理的控制方程的解。

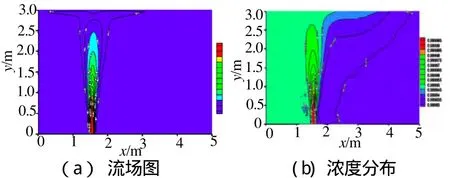
图3 催泪剂的流场图及浓度分布（z=0）Fig. 3 The flow field of the lachrymator and concentration distribution (at z=0)

图3（a）是在z=0的对称中心截面上的流场图，由图3（a）可知，由于室内流场的流速较低，所以基本上形成了以弹体释放源S处为中心，向两侧逐渐扩散的流场分布。这主要是因为对于本流场而言，外界流场的作用十分微弱，催泪剂主要是依赖自身的释放速度以及它们所受的重力、气体曳力以及随机力等各种作用力所驱动的，因此其不易扩散开来。图3（b）为对应的催泪剂浓度分布，图中通过颜色来表示催泪剂浓度的高低，颜色越接近蓝色代表催泪剂的浓度越低，反之，颜色越接近红色则表示催泪剂的浓度越高。由该图可知，由于形成的催泪剂不易扩散，因此其浓度较高，基本在0.7～0.9的范围内。

2.2 不同位置处的催泪剂浓度分布

图4为不同高度处y方向的催泪剂浓度分布，图4（a）为x=0.6m处，不同高度处y方向的催泪剂浓度分布；图4（b）为x=2.5m处，不同高度处y方向的催泪剂浓度分布。

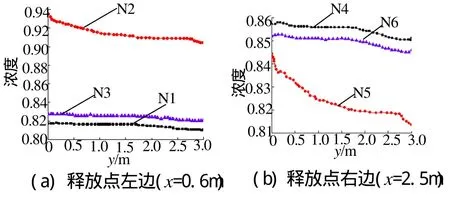
图4 不同高度处y方向的催泪剂浓度分布Fig.4 The lachrymator concentration distribution at y direction with different height

由图4可知，不同高度处y方向的催泪剂存在一定的浓度梯度。同时还可发现，N2和N5虽然都正对窗口，但是由于N5在释放点的右边，比较靠近窗口所在的截面，所以催泪剂较容易被窗口吸引而向外扩散，浓度相对其他位置来说明显较小。而N2虽然也正对窗口，但其位于释放点的左边正上方，且离窗口较远，故浓度较大。

图5为在高度y=1.1m处，不同前后处x方向的催泪剂浓度分布。

图5 x方向不同观测点处的颗粒浓度分布Fig.5 The concentration distribution at x direction with different observation point

由图5可见，在最前点和最后点的浓度变化不大，而在中间点处，呈现一种先增大，之后又不断减小的趋势。这主要是因为N11处的x方向浓度会先经过释放源位置，后又靠近窗口，故呈现出先增大后减小的趋势，而N10、N12水平方向，由于受气流影响较弱，故浓度较高，之后距离窗口处越来越近，故浓度也在逐步地减少，这一点与Fick扩散定律[8]：“粒子将由浓度高的地方向着浓度较低的地方不断迁移，使粒子浓度梯度逐步减小”是一致的。

但是，总体而言，由于催泪剂一直是处于室内，不受外界的其他影响，其主要是在重力、气体曳力及随机力等的作用下，进行随机扩散运动，因此各点位置的浓度均比较高，基本维持在0.7～0.9的范围内。

3 结论

本文采用Fluent软件对催泪剂扩散动力学特性进行了数值模拟，经计算分析得到以下结论：

（1）在自由扩散的情况下，室内形成了以弹体释放位置为中心，向两侧扩散的气流场和粒子浓度场，由于没有外界的影响，整个室内的浓度分布普遍较高，不易扩散。

（2）通过比较不同位置的催泪剂浓度，发现无论是竖直方向还是水平方向上，离通风窗口越近的位置，浓度越低。

（3）本研究为催泪剂的扩散特性研究提供了一种新的思路，但作为尝试，计算中未考虑催泪剂自身的影响，如催泪剂粒子之间的碰撞与凝并等效应，其还有待于进一步改进。

[1] Paramasivam Ravikumar , D. Prakash. Analysis of thermal comfort in an office room by varying the dimensions of the windows on adjacent walls using CFD: a case study based on numerical simulation[J]. Building Simulation,2009,2(3): 28-35.

[2] Yassin Mohamed F. Filtering effect of wind flow turbulence on atmospheric pollutant dispersion[J]. Environmental Monitoring and Assessment, 2011, 184 (6): 3749-3760.

[3] 吴晋湘,贾云飞,周波,等.室内可燃气体泄漏扩散的数值模拟[J].安全与环保,2007,31 (10):42-44.

[4] 王晓华.室内燃气泄漏扩散模拟分析[J].科学技术与工程,2012, 12 (32): 8785-8787.

[5] 蒋裕平,倪伟帆,方永腾.甲醛室内扩散的模拟分析[J].绿色科技, 2014 (3):89-90.

[6] 璠肖楚.自然通风条件下室内甲醛扩散模拟研究[J].洁净与空调技术, 2013 (1): 15-18.

[7] Bird G. A. Molecular gas dynamics and the direct simulation of gas flows[M]. Oxford: Clarendon Press, 1994.

[8] 卢正永.气溶胶科学引论[M].北京:原子能出版社, 1999.