基于ADCP的长江河口推移质运动特性研究
2015-03-22陆雪骏程和琴胡浩郭兴杰刘高伟吴帅虎
陆雪骏,程和琴,胡浩,郭兴杰,刘高伟,吴帅虎
(华东师范大学 河口海岸学国家重点实验室,上海 200062)
推移质运动是河流中泥沙运动的普遍形式之一,对地貌演变有重要影响,所以理解推移质运动对实际生产有着重要的理论指导意义。由于推移质运动处于水底床面附近,以往受限于观测方法和仪器条件,观测难度较大、耗资巨大,成为人类工程建设的一个技术难点。
传统推移质观测由于采样器的阻水作用,改变了床面运行的推移泥沙的水力条件,造成偏差(张瑞瑾等,1998),随着测量技术的发展,利用新型的测量仪器尝试观测推移质运动成为可能。国外Rennie 等(2002) 首先利用ADCP(声学多普勒流速剖面仪) 的底跟踪(Bottom Track) 功能观测河床推移质视速度(va),发现与传统采样器测的推移质输沙率有高度相关性,确认ADCP 观测推移质运动的可行性(Colin,2002;Colin,2004);国内吴中等(2002) 建立ADCP 的底跟踪和GPS 信号的联系,证实了利用ADCP 底跟踪与GPS 定位差距分析底沙运动的理论正确、方法可行(吴中等,2002)。ADCP 观测推移质方法优于传统采砂器测量方法,采用非侵入式手段,不破坏现场水流结构。在实际测量应用中,把ADCP 测得推移质运动视速度近似看作推移质运动速度(Kostaschuk,2005),对了解和掌握长江口推移质运动规律有重要意义。
本文采用定点测量方法,利用ADCP 对长江口砂质河床推移质运动进行观测,分析了推移质运动在涨、落潮周期内的变化情况。
1 数据采集
ADCP 的实测资料来自笔者所在课题组在长江口S1(长兴岛北侧)、S2(南北槽分流口)、S3(崇明东滩南侧)、S4(横沙岛北侧)、S5(南汇南滩) 和S6(横沙通道北侧) 共6 个测点的定点水文观测(图1) 资料,时间尺度为二个潮周期。S1、S3、S4、S5 测点于2012年6月6-7日测量,S2 测点于2013年7月10-11日测量,S6 测点于2013年7月1-2日测量。
此次数据采集使用的是美国RDI 公司生产的600 kHz 型ADCP,具体由WinRiver 软件对ADCP的换能器实现操控和采样,采样时间间隔设置为5 s,换能器入水深度为1 m。同时,采用高精度差分GPS 和外部GPS 罗经进行定位。
底层泥样采集采用帽式采集器,并用聚乙烯塑料袋密封存放。在实验室内,用超声波震荡分散,使用MASTER SIZER 2000 型激光粒度分析仪经行粒度分析。
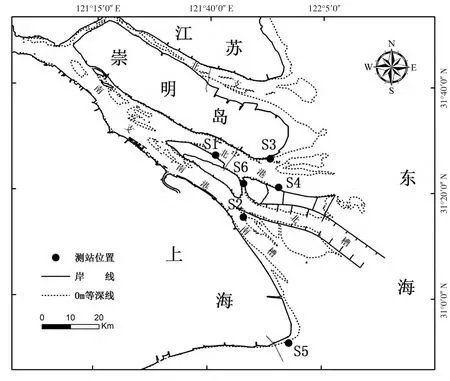
图1 长江口自然地理概况及测站位置
2 观测原理
ADCP 是目前世界上先进的流速流量测量设备,其利用多普勒原理探测水体中微颗粒的运动速度而推测水体流速。ADCP 提供两种方法测量安装平台的速度:一是“底跟踪”技术,ADCP 通过接收和处理来自水底的回波信号而计算得到ADCP 的安装平台与底床的相对速度(vBT);二是利用GPS全球卫星定位系统测量安装平台的速度(vDGPS)(赵胜凯 等,2007;杨俊辉,2009)。在测量时,如果床面没有推移质运动,那么ADCP 的安装平台相对于底床的速度等于安装平台参照GPS 得到的速度,即:
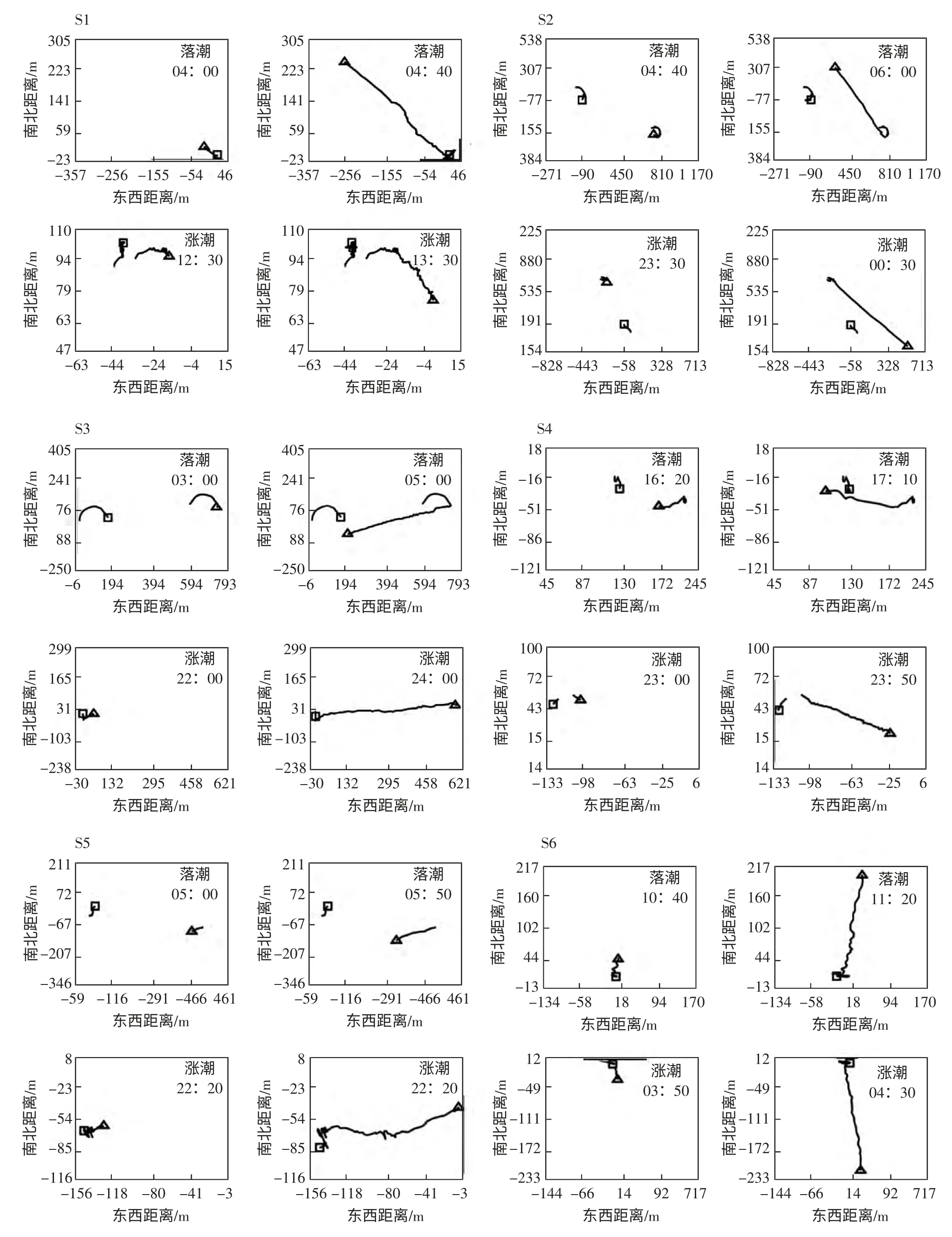
图2 各测点涨落急阶段航迹图(底跟踪航迹为三角形,GPS航迹为正方形)

如果是存在推移质运动的情况下,那么ADCP的安装平台相对于水底的速度和安装平台参照GPS得到的速度之间存在偏差,差值就是推移质运动速度(va) (Colin D,2002),即:

ADCP 所提供的测量速度有东西(ve)、南北(vn) 方向上的分量,利用公式计算出速度(Colin,2007):

3 结果
3.1 各测点航迹图
通过ADCP 数据处理软件WinRiver 查看航迹图,笔者选取了各站点观测期间涨、落急时段的航迹图(图3),三角形代表测量船参考底跟踪的航迹,正方形代表测量船参考GPS 定位的航迹。通过航迹图,能够观察到,底跟踪的航迹与GPS的航迹有明显的偏移,且各测点落潮与涨潮时刻的偏移方向是相反的。S1 测点落急时段,GPS 航迹基本不变,符合定点测量的事实;底跟踪航迹持续向西北方向延伸了一段距离,起点为(0,0),终点为(-256,230),航迹向西北方向移动了344 m,历时为2 400 s,由此可算出船的平均相对运动速度为0.51 m/s,即底床相对于测量船的运动平均速度为0.51 m/s。由此说明底床存在推移质运动。同样,S1 涨急时段和S2、S3、S4、S5、S6 涨、落急时段都存在推移质运动。
可见,在涨、落急时段流速较强、推移质运动速度较大时,ADCP 可以直观地观测到推移质运动速度变化,且通过观察水流流向(表1) 和底跟踪航迹偏移方向,可得出推移质运动方向和水流流向基本一致。
3.2 各测点潮流特征
S1、S2、S3、S4、S5、S6 测点处的潮流性质属于非正规半日浅海潮流,水流运动形式为往复流,涨落潮流向相反(沈焕庭等,1979)。观测数据显示(表1),受长江径流量及测点位置的影响,S1、S2、S3、S4 和S6 测点落潮平均流速一般比涨潮平均流速大;因S5 测点位于最大浑浊带的拦门沙区域,潮流和径流动力条件相当,故涨、落潮平均流速差别不大。S1、S2、S4 和S6 测点落潮最大流速与涨潮最大流速,分别相差0.56 m/s、0.12 m/s、0.29 m/s、0.16 m/s;S3 和S5 测点情况相反,涨潮最大流速比落潮分别大了0.11 m/s 和0.82 m/s。
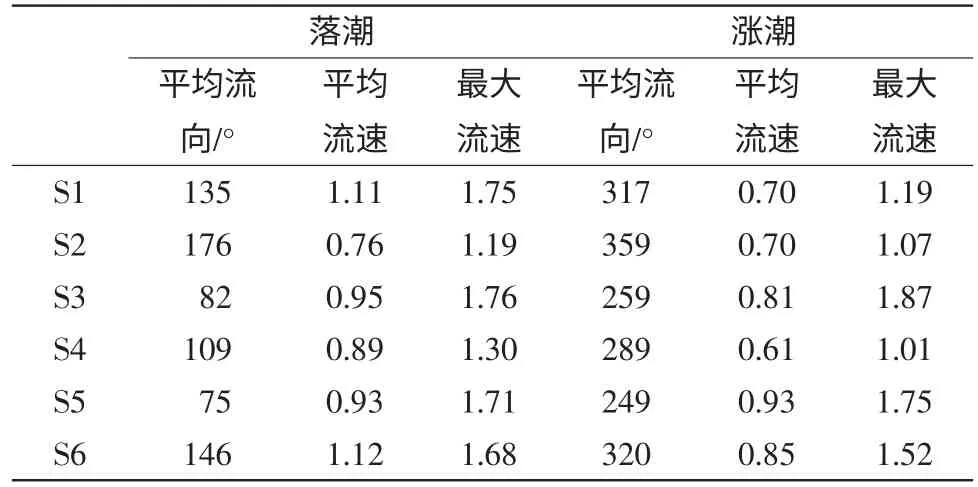
表1 各测点落潮、涨潮流速对比单位:m/s
S1、S2、S3 和S4 的流速过程线存在着明显的不对称现象,落潮流速过程线相对平缓且持续时间较长;涨潮流速过程线的顶峰明显且持续时间短,落潮流的强度超过涨潮流,落潮历时长于涨潮历时,强流速时间持续3~4 小时。涨、落潮流流向基本上与河槽主轴线平行。S5 和S6 测点涨、落潮流速过程线基本上对称,涨落潮峰值和持续时间都相近。
3.3 各测点床沙粒径
各测点床沙粒径统计如表2,S1 测点的中值粒径最大,D50=0.094 mm,为极细砂质。S6 测点的中值粒径最小,D50=0.010 mm,为中黏土质。所以此次研究讨论范围在粗粉砂至极细砂质河床。
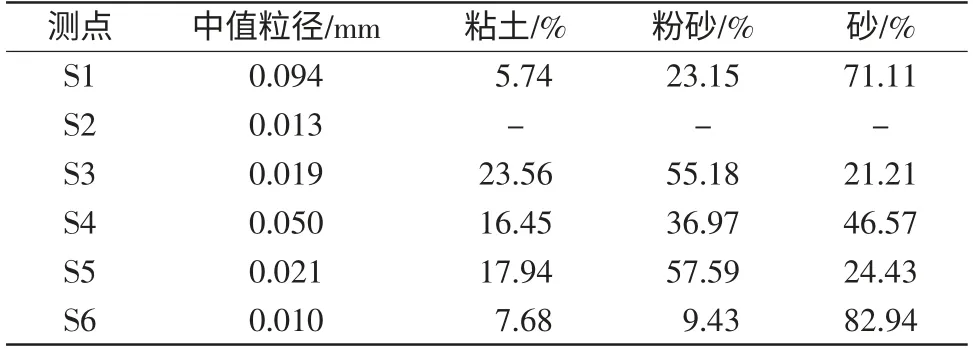
表2 各测点河床粒径统计表
4 讨论
4.1 推移质运动速度随流速变化过程
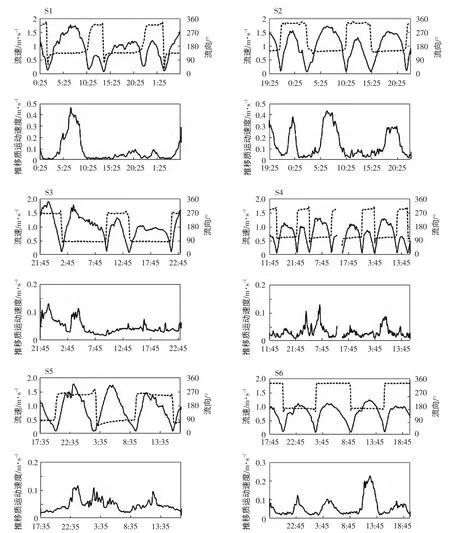
图3 各测点垂线平均流速(实线)、平均流向(虚线) 和推移质运动速度
通过公式(2) 和公式(3) 可计算出推移质运动速度,可以直观地看到推移质运动速度在潮周期内的变化过程(图3)。观察推移质运动速度变化过程曲线和潮流流速变化过程曲线,我们可以发现两者呈现“对应、不对称”的特征。
“对应”指在观测的二个潮周期内,各测点的推移质运动速度变化都与垂线平均流速变化一致,即在落急和涨急时段,推移质运动速度会达到最大值。但在S1(10 ∶25-15 ∶25)、S2(10 ∶25-15 ∶25) 测点的一次涨潮过程中和S3(7 ∶45-22 ∶45)测点的一次涨潮至落潮的变化过程中,推移质运动速度并没有明显的增大后又减小的变化过程,这与潮流流速和底质粒径大小有关,过小的流速不能使该测点底质发生推移质运动(钱宁等,1983)。
“不对称”现象指推移质运动速度变化历时比潮流流速变化历时短(表3),推移质运动速度变化过程曲线与潮流流速变化曲线比较,其峰值较尖。以泥沙起动流速为临界划分推移质运动状态(胡浩等,2014),当流速达到临界流速时,明显的推移质运动才会发生,这与测点的底质粒径大小有关(图4)。
各测点底质粒径与推移质运动起动临界速度形成反比趋势,受细颗粒泥沙之间的粘结力的影响,随着粒径的减小,也变得越来越不容易起动。
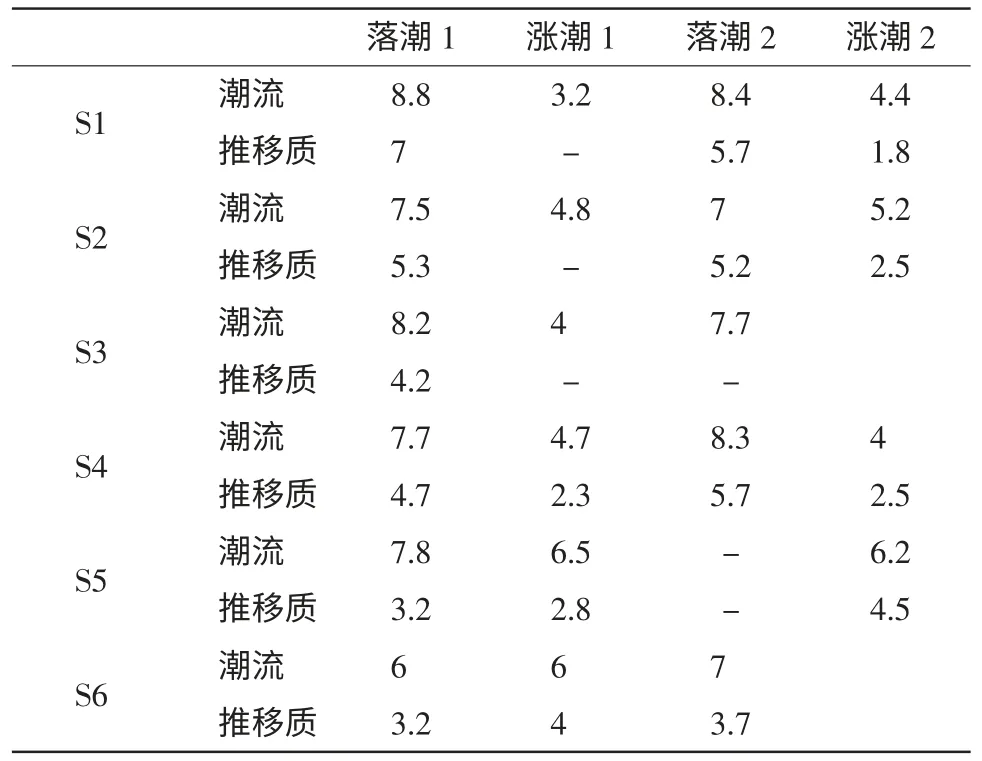
表3 各测点潮流、推移质运动速度变化历时单位:h
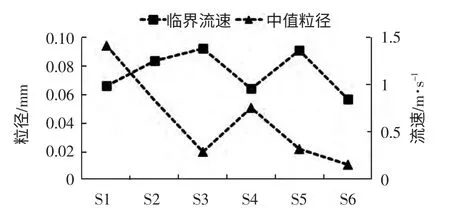
图4 各测点临界流速和中值粒径关系
4.2 推移质运动速度变化特征
表4 为各测点推移质运动速度的统计,S1、S2、S3、S4 和S6 测点落急的推移质运动速度均大于涨急的推移质运动速度,且落潮阶段推移质运动持续时间大于涨潮阶段(图3);S5 测点的推移质运动涨、落潮时段没有明显的差别,这与当地的潮流特征保持一致。
S1、S2、S3、S4、S5、S6 各测点受浅海、河口水下地形、径流等影响,潮流变化均有显著的潮汐不等特征,相邻的二次落潮或(涨潮) 的流速不等,导致了各测点相邻的二次落急(或涨急) 的推移质运动速度不等。这种不等在S1 和S3 测点体现得尤为明显,S1 测点第一次落潮推移质运动速度比第二次落潮推移质运动速度大了一个数量级(表4);在S3 测点,第一次涨落潮推移质运动速度明显大于第二次落潮推移质运动速度,甚至在第二次落潮和涨潮之间的推移质运动速度始终保持在一个较小的值,没有发生明显起伏变化(图3);同样,在S2 的两次涨潮时段和S4、S6 的两次落潮时段都出现了推移质运动速度日变化不相等的情况。在各测点,潮汐不等现象导致了推移质运动速度的日变化不等,又因为临界起动速度的存在,使推移质运动速度的变化不等现象比潮汐日不等现象更加显著,说明在较长时间尺度下,长江河口净推移质输沙方向与落潮流方向一致。
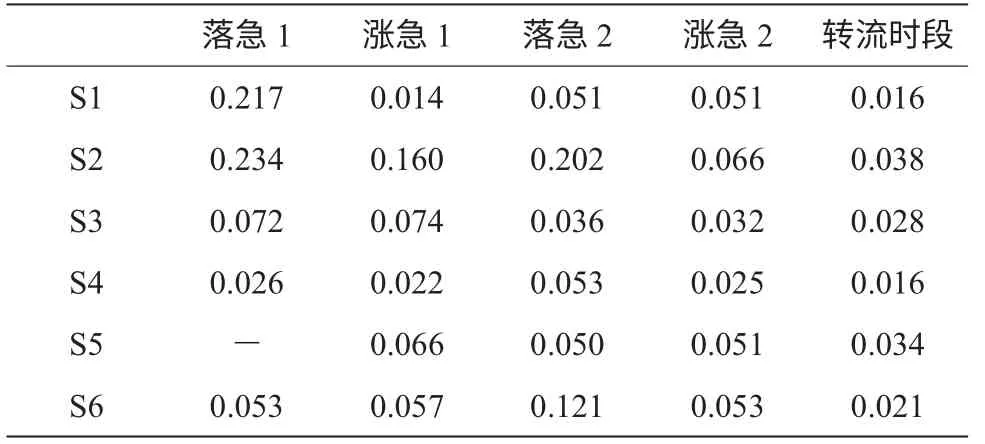
表4 各测点涨、落急时段推移质运动速度单位:m/s
4.3 误差分析
基于ADCP 测量推移质运动的误差主要由DGPS 系统误差、船体晃动产生的倾斜误差和ADCP 自身噪声组成。
在潮流转流时段,因为流速变小,甚至为零,所以实际推移质运动速度为零。但在图3 中我们可以看到,在各测点转流时段,推移质运动速度虽然小但不为零,这是因为GPS 存在误差,无法与底跟踪完全同步。可以认为在潮流转流时段,流速条件不足以发生推移质运动,而此时推算出的推移质运动速度就是绝对误差的下限,对实际推移质运动速度存在高估,通过计算高估值范围在0.016-0.038 m/s 之间(表4)。可见,S1 落急1,S2 落急1、涨急1、落急2 和S6 落急2 计算得出的推移质运动速度比高估值大了一个量级,具有较高的可信度。
5 结语
(1) 通过ADCP 多普勒流速剖面仪观测,在涨急、落急时段有明显的推移质运动,能直观体现半日潮对底沙运动的周期性影响。
(2) 推移质运动速度变化过程曲线和潮流流速变化过程曲线呈现“对应、不对称”的特征。
(3) 推移质运动速度的日不等现象比潮流流速日不等现象更加显著。
(4) 通过转流时段推移质运动不存在的特征,计算出使用ADCP 观测推移质运动速度的高估范围为0.016-0.038 m/s。
C.D.Rennie,F.Rainville,S.Kashyap,2007.Improved estimation of ADCP Apparent bed-load velocity using a real-time Kalman filter.Journal of Hydraulic Engineering. (12) :1337-1344.
Colin D.Rennie,Robert G.Millarand, Michael A, 2002.Measurement of Bed Load Velocity using an Acoustic Doppler Current Profiler Church.Journal of Hydraulic Engineering,128:473-483.
Colin D. Rennie, Paul V. Villard, 2004. Site specificity of bed load measurement using an acoustic Doppler current profiler. Journal of Geophysical Research,109.
Kostaschuk R,Best J,Villard P,et al, 2005.Measuring flow velocity and sediment transport with an acoustic Doppler current profiler.Geomorphology.May 15,68 (1/2) :25-37.
胡浩,程和琴,杨忠勇,2014.基于ADCP 的长江口推移质运动遥测技术研究.人民长江,45(14):6-9.
钱宁,万兆惠,1983.泥沙运动力学,北京:科学出版社.
沈焕庭,潘定安,1979.长江河口潮流特性及其对河槽演变的影响.华东师范大学学报(自然科学版),01:131-144.
吴中,陈力平,游目林,等,2002.底部浮泥表层推移速度分布的ADCP-GPS 估测方法.海洋工程,20(4):85-88.
杨俊辉,2009.ADCP、OBS 在底部泥沙运动观测中的应用探讨.港工技术,46(z1):90-93.
张瑞瑾,谢鉴衡.河流泥沙动力学.北京:中国水利水电出版社,1998.
赵胜凯,王志芳,2007.ADCP 基本原理及应用.河北水利, (11):25.
