利用不同类型的积分不等式计算相同定积分的精确值（13）

李平乐 李春晖

（娄底职业技术学院机电工程系教务处，湖南娄底 417000）

李平乐 李春晖

（娄底职业技术学院机电工程系教务处，湖南娄底 417000）

定理；同类、异类积分不等式的广泛应用；分解积分区间；精度

本文运用文献[13]中同类不等式的不等程度小于异类不等式的不等程度的性质再次验证了提高定积分近似计算精度的普遍性，当工程设计精度要求不高时，利用计算器手工计算即可，当精度要求很高时，可先将积分区间细分并建立计算的数学模型，然后再对数学模型编程，利用计算机进行数值计算，这样就把在理论上称之为求近似值的问题实质上转换为求精确值[1]-[22]，同时整理形成了该类函数的近似计算公式，为计算机编程提供了2个重要的数学模型。

1.主要结果

当角X在第一，三象限

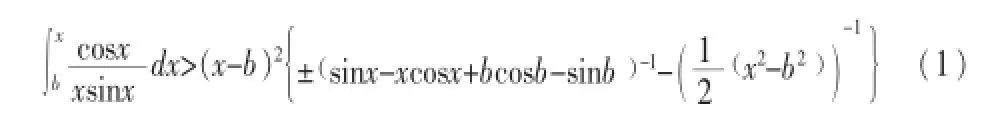
注：角X在第1像限，公式（1）第1项前取“+”号，

第2项前取“-”号。，角X在第3象限，公式（1）第1项前取“-”号，第2项前取“-”号。

注：角X在第2像限，公式（2）第1项前取“-”号，第2项前取“+”号角X在第4象限，公式（2）第1项、第2项前均取“+”号。

证（1）式

由文献[1]-[22]的性质以及文献[13]中同类不等式的不等程度小于异类不等式的不等程度的性质得[3]式

为帮助读者尽快掌握知识并加深对文献[1]-[22]性质的认识，再对（3）式五处做小范围说明由文献[1]-[22]性质得

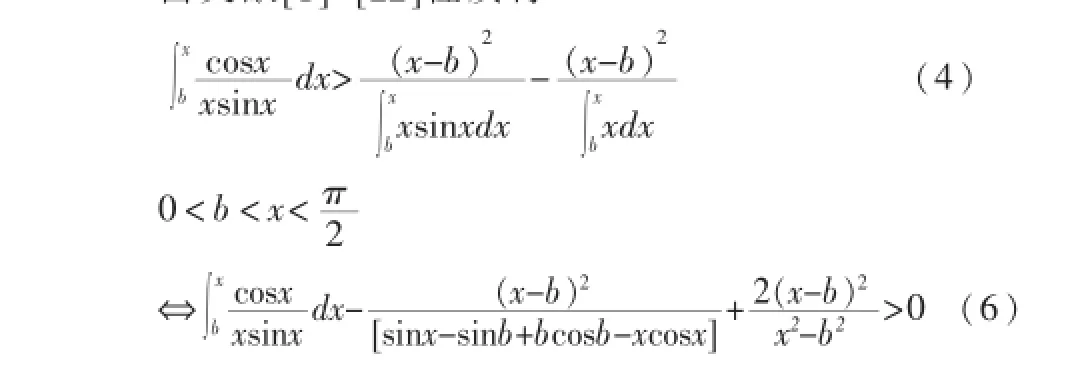
为书写简便，令（6）式第二项分母为[A]，这样（6）可写成：

上单调增加，（4）式成立，

［注：（sin x+cos x）-1＞0］

证明（8）式大于零，只需证明

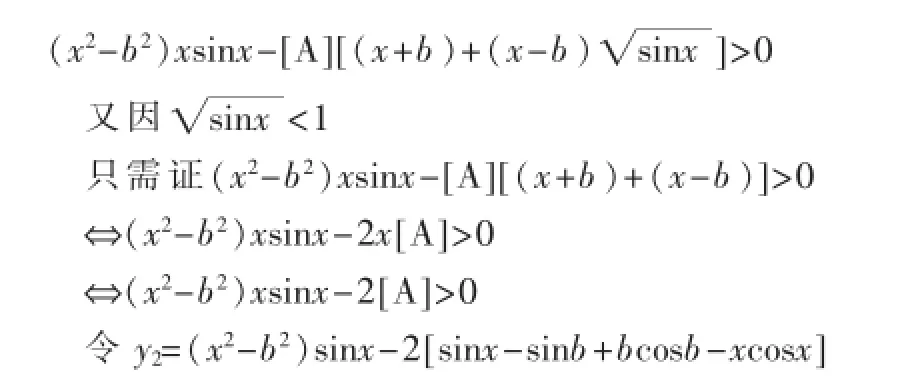
由文献[1]-[22]性质得：

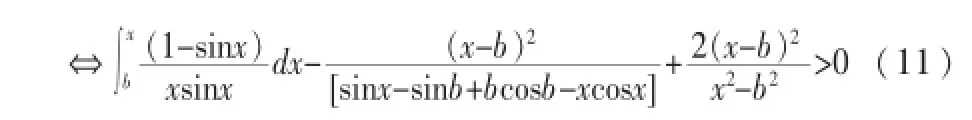
为书写简便，令（11）式第二项分母为[A]，这样（11）式可写成：

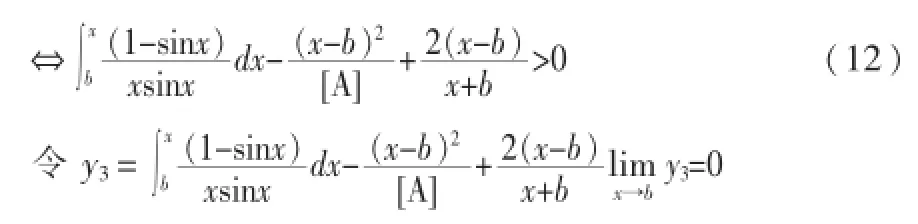
上单调增加，（10）式成立，

从（13）式可看出，（13）式分母大于零，（13）式分子第二项大于零。

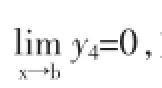
通过对（3）式部份项求定积分

2.计算实例

解由（2）式得

分别代入（2）式计算结果为

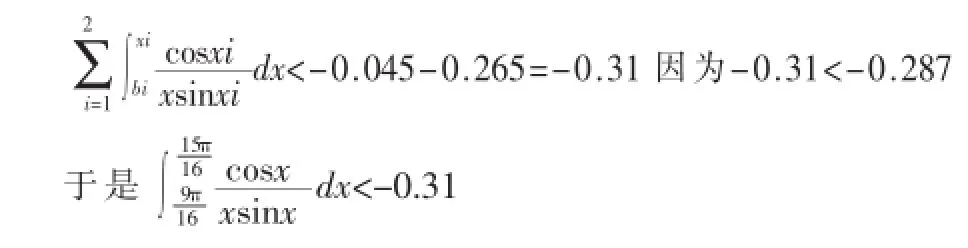
可见将（2）式积分区间2等分，积分误差减小，数值-0.31更接近于积分精确值，若将（2）式积分区间进一步分细，积分误差更小，略。

解由（1）式得

积分区间未等分，积分误差最大，现将(1)式积分区间2等分

分别代入（1）式计算结果为

因为0.206＞0.135

可见将（1）式积分区间2等分，积分误差减小，数值0.206更接近于积分精确值，若将（1）式积分区间进一步分细，积分误差更小，略。

3.结语

[1]李平乐.关于一类积分的近似计算及误差确定的第三种论证方法[J].西北师范大学学报：自然科学版，科研与教学论文专辑，2008，（41）：5-19.

[2]李平乐.新的积分近似计算方法在工程设计中的应用之一[J].太原师范学院学报：自然科学版，2008，7(3)：37-39.

[3]李平乐.基于积分近似计算在工程设计领域的研究[J].吉首大学学报：自然科学版，2008，29(6)：4-6.

[4]李平乐.基于积分近似计算在工程设计领域的研究[J].西北师范大学学报：自然科学版，科研教学论文专辑，2008，（42）：8-11.

[5]李平乐.关于一类积分的近似计算及误差确定的第三种论证方法在工程设计中的应用之一[J].沈阳工程学院学报：自然科学版，2009，5(2)：187-189.

[6]李平乐.基于工程设计计算的新的积分不等式与数学模型的研究[J].太原师范学院学报：自然科学版，2009，8(3)：32-35.

[7]李平乐.工程设计计算方法的精度分析[J].沈阳工程学院学报：自然科学版，2010，6(1)：94-96.

[8]李平乐.定积分换元与新的积分不等式结合在工程设计计算中的应用[J].焦作大学学报，2010，(1)：114-115.

[9]李平乐.对多类积分不等式求解工程设计同一值的研究[J].太原师范学院学报：自然科学版，2010，9(4)：40-43.

[10]李平乐.用积分不等式计算一类定积分的值[J].湖南工业大学学报，2010，24（5）：37-41.

[11]李平乐.工程设计中新的积分不等式的应用和计算分析[J].沈阳工程学院学报：自然科学版，2011，7(1)：93-96.

[12]李平乐.基于工程设计计算新的积分不等式的研究[J].沈阳工程学院学报：自然科学版，2011，7（4）：382-384.

[13]李平乐.新的积分不等式在工程设计中的应用[J].淮海工学院学报：自然科学版，2011，20（3）：6-10.

[14]李平乐，汤世行.定积分近似计算需求计算公式的建立[J].焦作大学学报，2012，（4）：90-92.

[15]李平乐.工程设计中一类定积分的近似计算[J].湖南工业大学学报，2012，26（1）：6-9.

[16]李平乐.基于工程设计计算新的数学模型研究[J].沈阳工程学院学报：自然科学版，2012，8（4）：381-384.

[17]李平乐.利用诸多函数求解一类积分的近似值[J].西北师范大学学报：自然科学版，科研与教学论文专辑，2012，（48）：6-8.

[18]李平乐.计算机编程的新的数学模型的探索与实践[J].西北师范大学学报：自然科学版，科研与教学论文专辑，2012，（48）：9-12.

[19]李平乐，罗正斌，龙育才.工程设计计算新的数学模型的研究[J].焦作大学学报，2013，（1）：70-72.

[20]李平乐.新的积分不等式求解工程设计精确值分析[J].沈阳工程学院学报：自然科学版，2013，9（1）：92-96.

[21]李平乐，李春晖.工程设计近似计算精度的探索[J].沈阳工程学院学报：自然科学版，2013，10（4）：374-377.

[22]李平乐，李春晖.另一类积分不等式在工程设计中的应用[J].焦作大学学报，2014，（1）：80-83.

[23]陆庆乐.高等数学（工本）[M].西安：西安交通大学出版社，1999.

[24]同济大学数学教研室.高等数学[M].北京：高等教育出版社，1988.

[25]丁鹤龄.高等数学[M].北京：高等教育出版社，1982.

（责任编辑 陈永康）

O1 72

A

1008-7257（2015）01-0087-03

2014-10-01

李平乐（1955-），男，湖南涟源人，娄底职业技术学院机电工程系高级讲师。