基于GIS的公路边坡危险性分析与预警系统研究
2015-03-21王卫东李大辉谭捍华龙万学
王卫东, 刘 超, 李大辉, 谭捍华, 罗 强, 龙万学
(1.中南大学 土木工程学院, 长沙 410075; 2.高速铁路建造技术国家工程实验室, 长沙 410075;3.贵州省交通规划勘察设计研究院股份有限公司, 贵阳 550081; 4.贵州省交通厅,贵阳 550003)
王卫东1,2*, 刘 超1, 李大辉1, 谭捍华3, 罗 强4, 龙万学3
(1.中南大学 土木工程学院, 长沙 410075; 2.高速铁路建造技术国家工程实验室, 长沙 410075;3.贵州省交通规划勘察设计研究院股份有限公司, 贵阳 550081; 4.贵州省交通厅,贵阳 550003)
从宏观方面,针对滑坡易发性区划,选择高程、坡度、岩性、地质构造、铁路建设和年均降雨量6个致灾因子及其二级指标建立滑坡敏感性区划研究体系,以主客观综合权重方法为原型构建滑坡敏感性区划GP模型,并发布为网络服务,在WebGIS系统中调用该服务自动编制滑坡敏感性区划图.从微观方面,针对单体边坡,使用地理力学方法对边坡的稳定性进行计算与分析.然后根据已有监测数据,运用预测模型,判断滑坡所处阶段,确定滑坡预警级别.该文将地质灾害宏观区划与单体边坡稳定性分析以及监测预警相结合,运用到公路边坡信息管理系统中,从而实现对公路边坡的危险性分析和灾害预警.
边坡信息管理; 地质灾害区划; 稳定性分析; 危险性评价; 监测预报
随着全国大范围高速公路的建设,山区高速公路逐渐增多,由于高速公路技术标准较高,高边坡问题难以回避,尤其是在较复杂的地质条件下.除了在设计阶段采取必要措施处理边坡外,已建、在建的高速公路中边坡的维护、管理及动态监测已引起了相应业主的重视.本文研究并实现了地质灾害易发性区划基于GP服务的网络化和自动化,重点边坡的监测数据分析处理和灾害预警预报功能,用户仅需浏览器便可使用,方便有关部门及时得到预警预报信息.
1 系统结构设计
本系统采用B/S(浏览器/服务器)架构,其核心是服务器端,包括了数据库和GIS服务,系统自上而下分为3层结构,即表现层、控制层和数据层,系统结构见下图1.
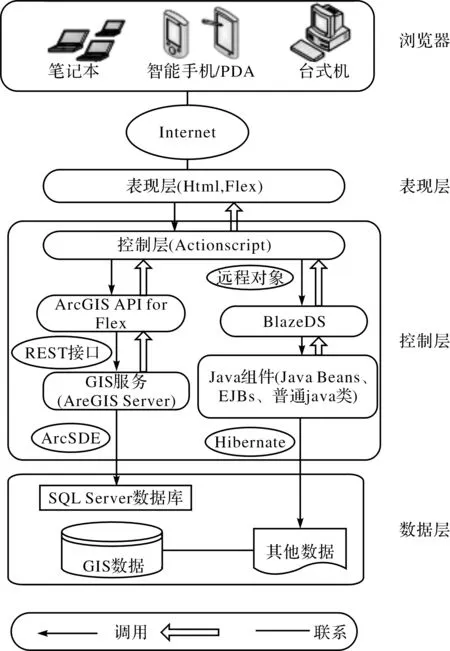
图1 贵州山区高速公路边坡地理信息系统架构图Fig.1 The architecture diagram of highway side slope geo-graphic information system of Guizhou province
系统功能结构主要包括基础地理信息管理、灾害易发性区划信息管理、边坡信息管理与稳定性分析和边坡监测管理与预测预报4大部分,见图2所示.其中,基本地理信息管理是系统的基础部分,主要完成对地理信息数据的管理与空间表现;灾害易发性区划信息管理主要通过调用地理处理服务,完成对研究区域的地质灾害易发性区划,并结合降雨量实现地质-气象耦合预警预报;边坡信息管理与稳定性分析模块基于地理信息数据库,实现对边坡的可视化管理,并进行边坡稳定性分析与分级;监测管理与预测预报模块则是对重点边坡进行监测管理,并结合预测预报模型对监测数据进行分析,从而实现预测预报.
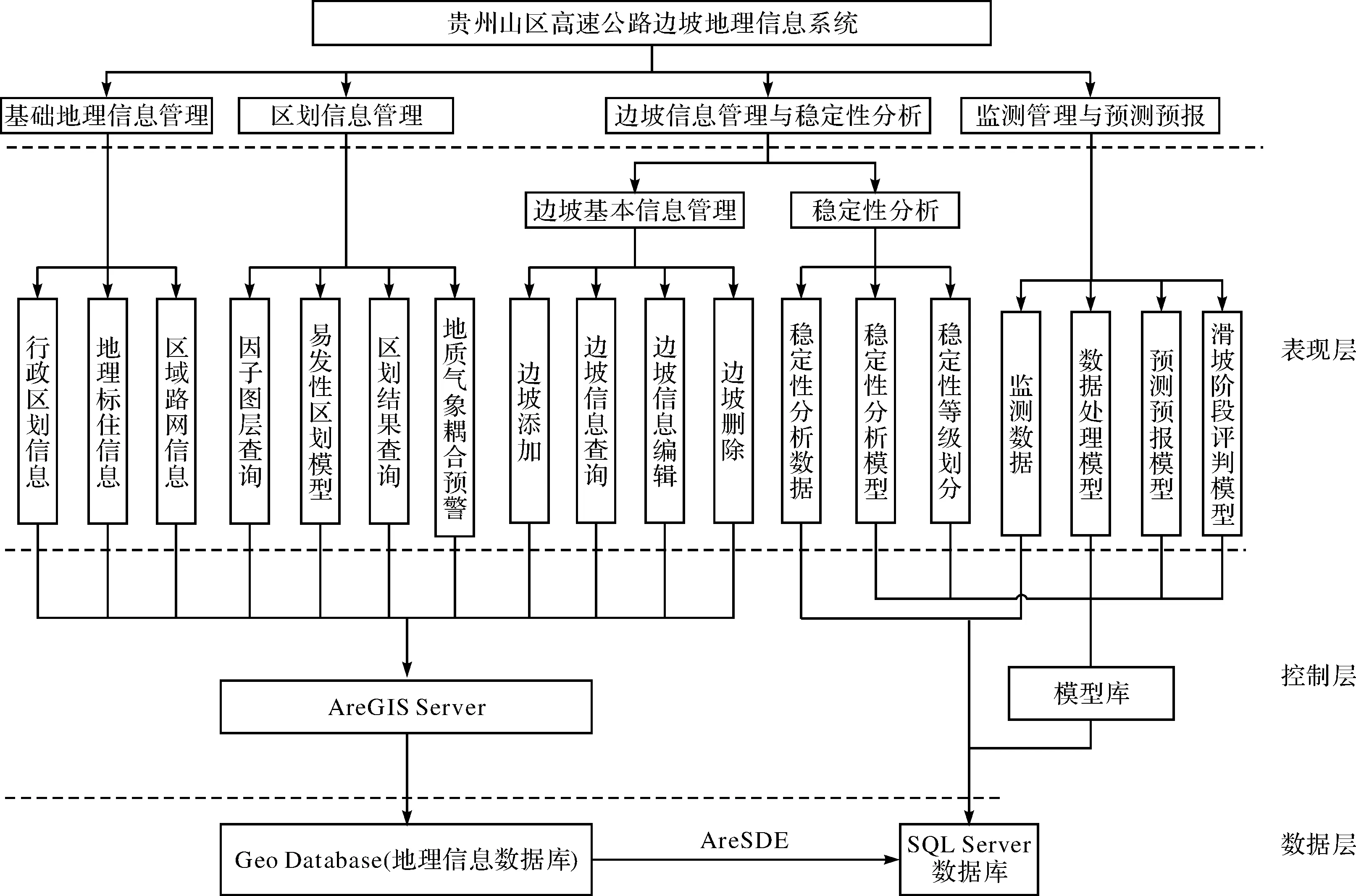
图2 贵州省滑坡灾害区划及边坡稳定性分析系统功能结构图Fig.2 The functional structure diagram of landslide hazard mapping and slope stability analyzing system of Guizhou province
2 区域灾害易发性区划
灾害易发性区划是从宏观角度出发,对区域地质灾害易发程度划分的一种方法,区划结果可以为区域公路路网规划和防灾减灾工作提供重要的决策依据.本文在考虑研究区域致灾因素(地形地貌、地质条件、水文环境等)的基础上加入灾害诱发因素(降雨、人工活动等),通过ArcGIS软件构建地理处理模型对研究区域内滑坡灾害发生的可能性进行分析和评级,形成贵州省滑坡灾害易发性区划图.
2.1 GP服务
本文通过对收集到的边坡数据加以汇总,并参考专家意见,可以得出边坡基本信息主要分为6大类,即边坡所处地理位置,包括坐标、行政区划等;边坡基本特征,包括长宽、体积、坡度等;边坡的一般分类,包括物质组成、运动方式、形成年代等;边坡的环境条件,包括周围环境、地下水动态、植被覆盖率等;边坡的整治措施,包括治理措施、效果、日期等;以及边坡的一些其他信息,包括养管单位、信息填写人等信息.对于这些边坡基本信息,系统都设置了增加、删除、查询、修改等功能,可以减少数据库的冗余,保证数据库存储数据的质量,并且系统中还设计了自动填写和错误自动检测等一系列功能,可有效避免错误的信息存储,从而保证数据库存储信息的完整和准确.
GP服务是指在ArcGIS Server平台下二次开发地理处理服务.GP(地理处理)服务提供GIS 分析功能,强调地理数据与用户的交互性,能充分挖掘隐藏的地理信息,其分析结果为决策提供依据[1].GP 服务所封装的分析功能通过商业GIS软件的二次开发实现,可提供研究领域内的GIS分析过程[2].与其他服务相比,GP服务是地理信息网络服务的高级应用和核心模块,相当于一般网络信息系统中的模型库.ArcGIS 提供了多种GP工具和可视化的GP建模环境,供专业人员进行GP 模型二次开发.用户可将GP工具组合成复杂的GIS工作流(图3),其中圆角矩形框代表GP 工具,椭圆形代表输入/输出数据,六边形表示中间数据,字母P标识整个模型的输入/输出参数[3].
研究采用Python语言开发脚本工具调用GIS底层组件,用于扩展GIS功能和实现主客观综合权重方法的数学计算.GP模型在服务器端构建之后,通过ArcGIS Server Manager 发布为GP 服务.
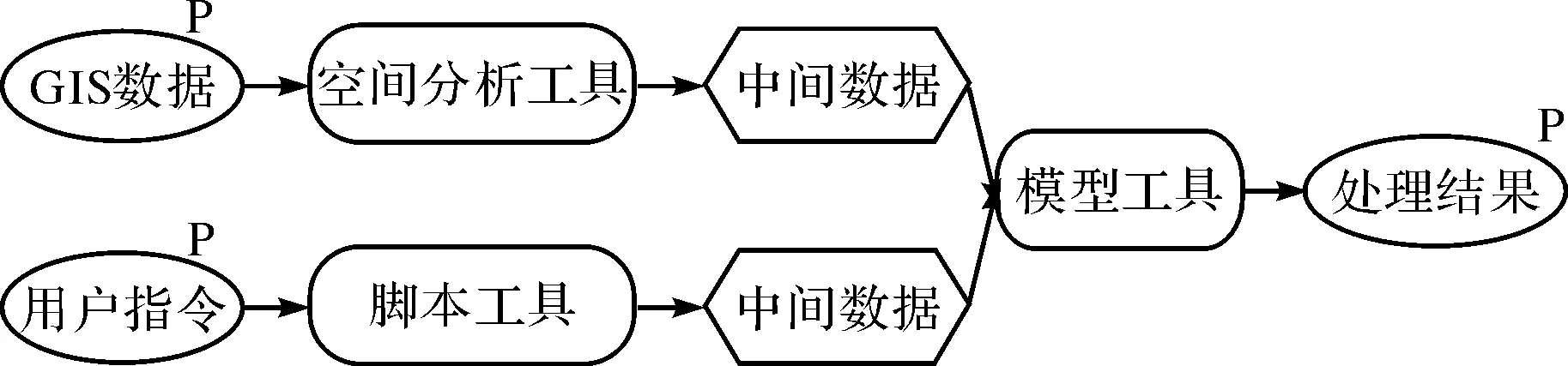
图3 地理处理建模示例Fig.3 Geoprocessing modeling example
2.2 区域致灾因子体系
控制和影响地质灾害孕育发生的主要影响因素可以归为3大类,即环境因素、诱发因素和历史因素.选取高程、坡度、岩性和地质构造4个环境因素,年均降雨量和工程建设2个诱发因素作为滑坡主要致灾因子[4].同一因子取值不同时对滑坡发生的影响程度不同,因此,需要将各一级因子进一步划分为若干二级因子.其中地质构造、工程建设分别以到地质构造线距离和到线路距离来划分二级因子.岩性等致灾因子作为地质变量,必须对其进行量化.由于各因子的测量单位不一致,导致每个因子的表现力不同,因此,还需要统一量纲[5].分级后的致灾因子体系如图4所示,在因子图层属性表中使用对应的因子标识表示各二级因子地理区域,本文重点介绍基于该致灾因子体系的GP模型建立过程.
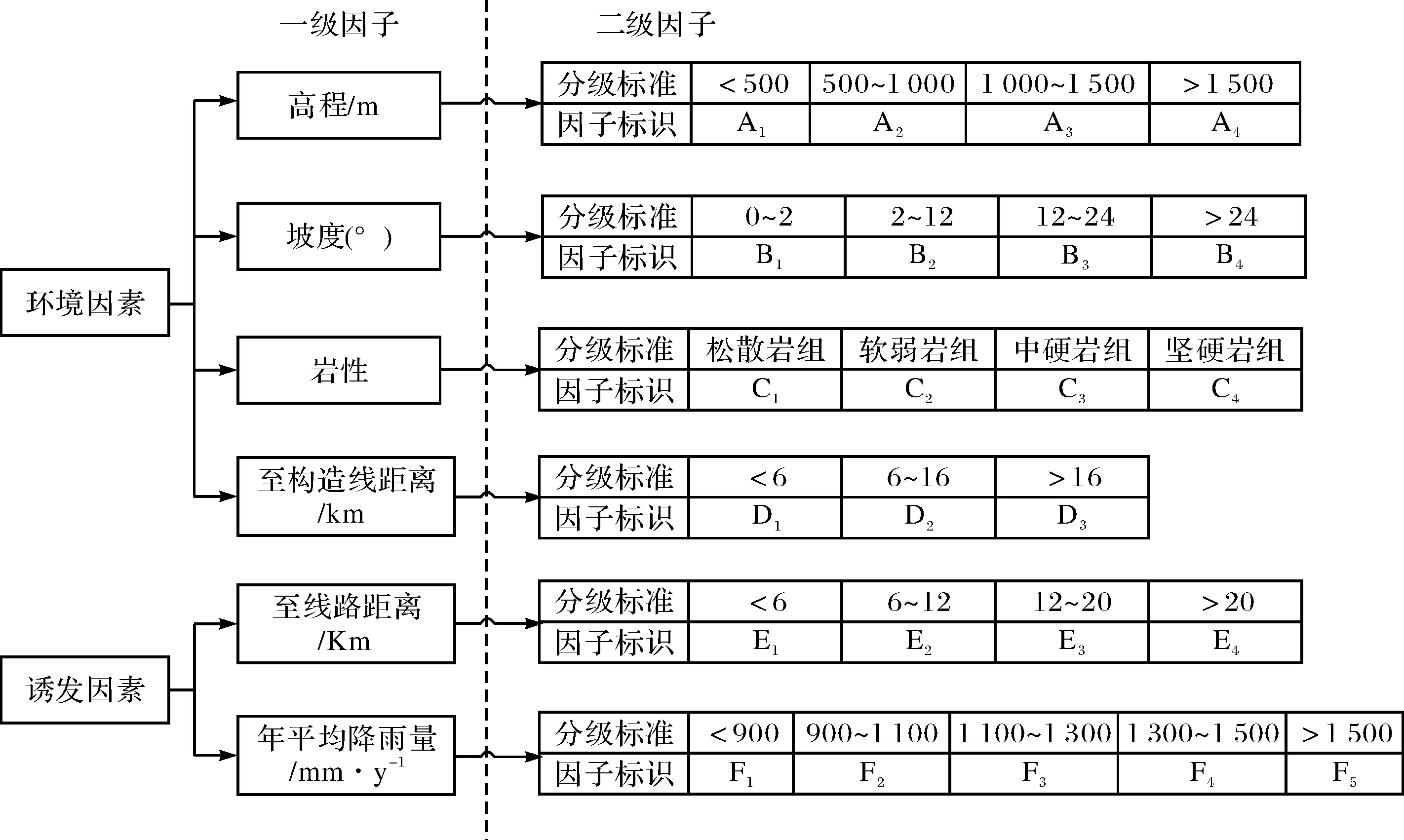
图4 滑坡致灾因子体系Fig.4 The landslide disaster-inducing factor system
2.3 构建区域滑坡易发性GP模型
本文主要采用主客观线性加权方法构建GP模型,该方法基于客观的熵值法和主观的模糊理论,是客观方法与主观方法的有机结合.根据熵值理论[6-7],致灾因子的客观权重由二级因子区域内历史灾点面积密度的熵值大小决定,统计各二级因子的面积以及各二级因子区域内历史灾点的面积,计算每个二级因子区域内历史灾点的面积密度,归一化后得到致灾因子的熵值,即可得到各致灾因子的客观权重.致灾因子的客观权重确定后,还需要对各因子的二级权重进行计算.二级因子权重为采用主观赋权的方法,即需要决策者和行业专家参与,对各致灾因子的二级因子采用梯形模糊数进行主观评价,再根据专家评价计算二级因子的权重.
主客观滑坡易发性模型涉及到地理信息图层的处理和因子权重的计算,前者需要对图层信息进行分析与操作,后者则需要对地理信息要素属性进行操作,这正是地理处理的优势所在,所以主模型基于地理处理创建.本系统滑坡易发性区划的主模型主要分为4个部分,如图5所示.
图中第1部分为致灾因子图层的叠置.每个致灾因子被划分为几个不同等级的二级因子,即是将研究区域划分为形状、大小均不相同的几个区域.将这些划分方式不同的图层进行叠置,整个研究区域将被划分为多个形状不规则的小区域,而这些小区域分别对应6个致灾因子的某一个二级因子.第2部分是各致灾因子二级因子的权重计算.根据权重线性组合原理,将致灾因子客观权重和其二级因子主观权重对应相乘,即可得到该二级因子在最终进行叠置计算时需要的权重,直接为后续区域权重叠置提供数据支持.第3部分是主模型的关键,负责计算图层叠置后所有区域对与滑坡易发性的贡献程度,即权重.“字段计算”工具为ArcGIS地理处理工具集中提供的系统工具,用来计算地理要素字段的数值,前面6个“字段计算”工具以近似循环的方式计算每个区域所对应的二级因子的权重,最后将同一区域内6个致灾因子的权重叠加,从而得出每个区域内滑坡易发性的综合权重.第4部分根据等间距法以各区域内的综合权重进行滑坡的易发性等级划分,并对不同等级进行渲染,最终形成滑坡易发性区划图.
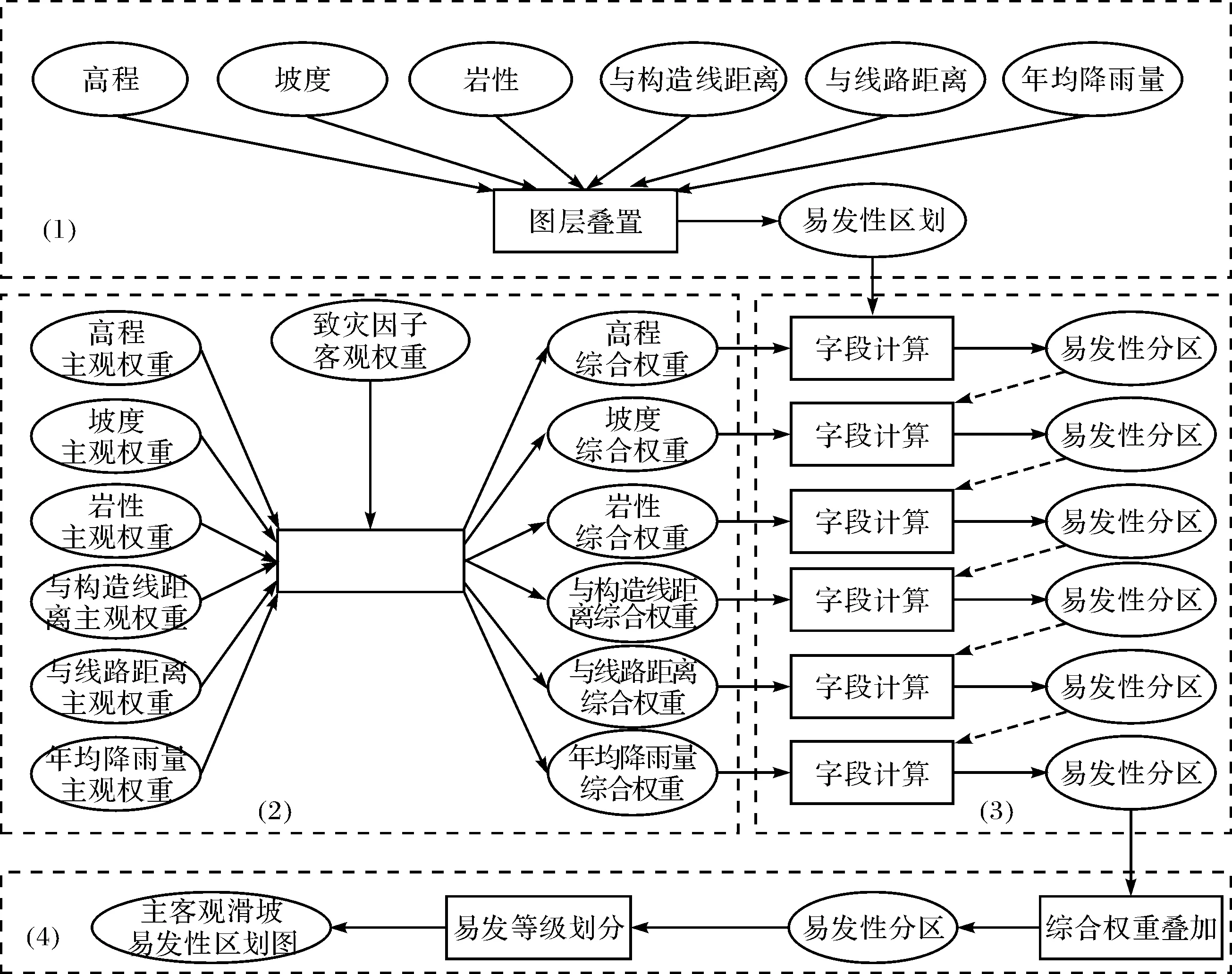
图5 滑坡易发性区划主模型Fig.5 The landslide susceptibility mapping master model
3 单体边坡稳定性分析
国内外稳定性分析方法众多,可分为确定性方法、不确定方法、有限元方法等,本系统中主要使用工程经验类比法、模糊综合评判法、Sarma法、Bishop法、传递系数法和简布法等6种方法构建边坡稳定性分析模型库,用户可以根据具体边坡情况选择评价方法.根据分析结果,对危险边坡及时采取防护和加固措施,避免灾害发生带来的损失,并可选择对重点边坡进行监测管理.
3.1 Sarma法
Sarma法可用于确定各种形式的边坡稳定性分析,属于极限平衡法.它认为边坡岩体的滑动面为理想的平面或圆弧面,从力学角度分析,岩体发生滑动时,不仅滑动面上的剪力平衡被破坏,同时也考虑滑动岩体内部的剪切.进行条块分割时,条块边界无需垂直,从而Sarma法可以对各种特殊的岩体结构进行稳定性分析,也可以对外部荷载下的边坡进行分析[8-9].
Sarma法通过假定对边坡施加一个水平体积力,来实现边坡的极限状态,体积力如水平地震惯性力等,为滑坡体的自重.对于边坡中的任一条块,其几何尺寸通常由3~4个顶点确定,地下水位线也可以在条块剖面上确定,在Sarma法中,这些点都以坐标的形式确定.具体条块尺寸及条块受力分析如图6所示.
根据条块的力学条件和几何条件,以及静力平衡条件:
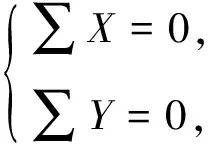
(1)
可以求得:
(2)
Sarma法为隐式算法,需不断折减抗剪强度,使边坡逐步达到极限状态,以此来求解稳定性系数.设折减系数F,将条块本身的强度参数c值与φ值同时按折减系数F进行折减,即同时以cbi/F、csi/F、csi+1/F、tanφbi/F、tanφsi/F和tanφsi+1/F代替cbi、csi、csi+1、tanφbi、tanφsi和tanφsi+1,作为新参数代入式(2)进行计算.经过多次迭代,使得等于边坡的实际水平地震系数,此时的折减系数即为该水平地震系数条件下边坡的稳定性系数[10].

图6 Sarma法条块尺寸及受力分析Fig.6 The size and force analysis of every strip-unit of slope by Sarma method
3.2 构建边坡稳定性分析模型库
系统中使用Matlab对上述稳定性分析模型进行后台算法的编写,构建边坡稳定性分析模型库,同时使用MXML搭建前台用户界面,完成选择和使用模型进行稳定性分析.
工程经验类比法主要依靠对已有的自然边坡或人工边坡进行调查分析,比较后确定研究边坡的稳定性状况,不牵涉数学模型的计算[11],系统中以界面输入方式实现对该方法稳定性分析结果存储.模糊综合评判法计算过程主要包括评价因素选择、判断矩阵输入、权重计算和隶属度计算等步骤,牵涉到的数学模型有矩阵计算和隶属度计算两部分,可直接使用ActionScript语言编写.
Sarma法、Bishop法、传递系数法和简布法都属于定量分析法的范畴,需要通过Matlab构建模型,并研究模型的输入参数与输出结果形式,构建前台界面,下文以Sarma法为例介绍模型的构建方法.
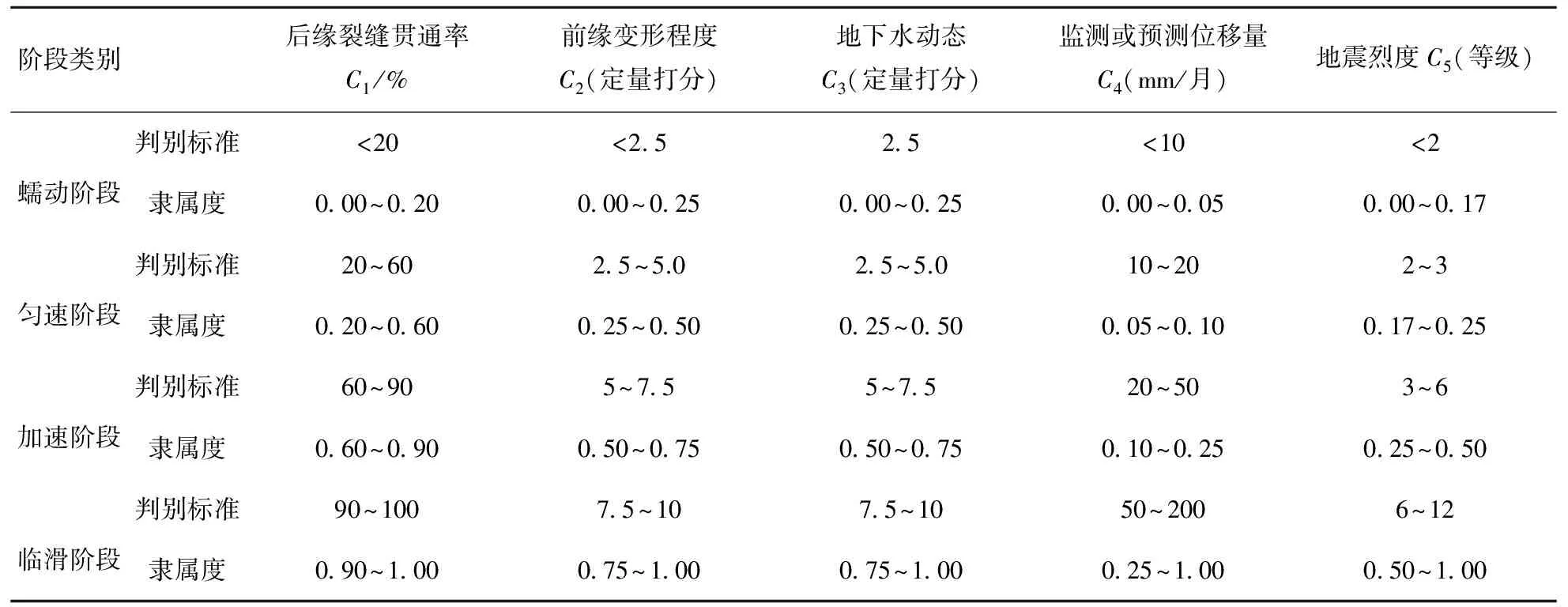
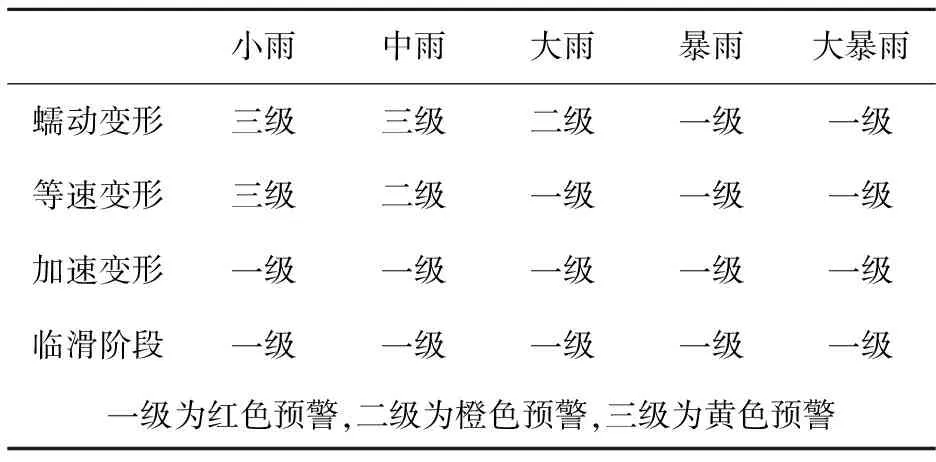
根据Sarma法计算原理,首先考虑值与值不折减的情况,即F=1,计算此时的水平地震系数Kc值.Kr为当地水平地震系数(不考虑地震时取0),若Kc>Kr,则以一定的步长递增;若Kc 重点边坡监测管理分析与预测预报主要是对较为危险的监测边坡进行管理.前文从宏观区划和微观单体边坡稳定性两个方面确定了危险边坡之后,从数据库提取已有监测数据,根据数据序列等间隔化和数据序列突变现象处理模型等方法对监测数据进行分析成图,从而可对监测边坡的变形状况进行判断.可选择预测预报模型对边坡变形位移进行预测,展示预测的位移时间曲线图,并根据边坡体变形理论判断所处变形阶段,结合降雨量外部因素判断边坡的预警级别. 4.1 监测边坡信息管理与数据分析 目前,常用的边坡监测方法有:钻孔测斜法、大地测量法(全站仪)、气象监测、地表水动态监测法和地表巡视等.系统为不同监测方法提供相应的模块进行监测数据的分析处理.例如:钻孔测斜法根据录入的监测数据,自动生成深度位移曲线、位移时间曲线、速度时间曲线和S.Q.H关系曲线. 4.2 滑坡位移预测 生成各种关系曲线图后,用户可选择适当的预测预报模型对监测点位移进行预测.系统主要采用了非线性回归分析法、BP神经网络法和Verhulst函数预测模型构建预测模型进行短临期位移预测预报,采用指数平滑法和灰色GM(1,1)预测法构建预测模型进行中短期位移预测预报.在本示例中,可以对各个深度点的位移量进行预测,从而可生成该监测点的位移时间曲线,下图7为采用灰色GM(1,1)模型预测的CXK4监测点5.5m深度处的位移时间曲线. 图7 晴隆滑坡CXK4监测点5.5 m深度处位移时间预测曲线图Fig.7 Displacement and time prediction curve at the 5.5m depth of CXK4 monitoring point of Qinglong landslide 4.3 判别滑坡变形阶段 本文中滑坡变形阶段的判别是基于可拓学综合评判模型.可拓学的基本思路是首先根据待评价事物的数据资料将事物质量分成若干等级,并确定各等级的数据范围,再对待评事物进行多指标评定,评定结果按它与各等级集合的关联度进行比较.关联度越大,它与某等级集合的符合程度愈佳[13]. 4.3.1 评判因子的隶属度化 滑坡分为4个阶段:蠕动阶段、匀速阶段、加速阶段和临滑阶段.本文确定的滑坡变形阶段的5个判别因子分别是后缘裂缝贯通率、前缘变形程度、地下水动态、位移量、地震烈度.本文中4.2即是通过GM(1,1)模型预测位移量C4. 确定了各判别因子对应滑坡各阶段的判别标准之后,为了方便评价,将这些判别标准进行隶属度变化,如表1所示. 根据现场监测数据,确定待评灾点晴隆滑坡的各判别因子的取值,并进行隶属度变化,如表2所示. 表1 判别因子对应的判别标准与隶属度 表2 晴隆滑坡各因子对应的隶属度 4.3.2 待评滑坡灾点变形阶段的确定 根据式(3)待评灾点各因子与各变形阶段的关联度公式,计算待评灾点各因子与各变形阶段的关联度.其中aoji和boji是变形阶段j对应判别因子ci的隶属度的最小取值和最大取值.api和bpi是各变形阶段对应因子ci的最小取值和最大取值.xi是待评物元对应因子ci的隶属度. (3) 其中, i=1,2,3,4,5;j=1,2,3,4; 由上述公式计算得到待评灾点各因子与各变形阶段的关联度矩阵如表3所示. 表3 晴隆滑坡各因子与各变形阶段的关联度 在得到待评灾点各判别因子与滑坡变形阶段的关联度矩阵之后,根据公式(4),计算得到待评灾点与变形阶段j的关联度: (4) 本文中,晴隆滑坡各因子的权重为=[0.15,0.16,0.23,0.3,0.16].因此,可以得出晴隆滑坡与各变形阶段的关联度如下所示.评定结果按它与各等级集合的关联度进行比较.关联度越大,它与某等级集合的符合程度愈佳.晴隆滑坡与匀速阶段的关联度最大,所以系统评价晴隆滑坡处于匀速变形阶段. 表4 晴隆滑坡与各变形阶段的关联度和评价结果 4.4 滑坡预警 确定了滑坡的变形阶段之后,结合降雨强度进一步确定滑坡预警级别.预警级别确定标准如表5所示. 表5 滑坡预警级别划分 本文介绍了一个高速公路边坡信息分析与管理系统.该系统以贵州省为研究区域,结合贵州主要公路网,在历史滑坡灾害分布规律的基础上,对其成因和易发性规律进行了相关研究,基于ArcGIS软件平台,构建基于主客观最优组合赋权的可拓学模型,并发布为地理处理服务,实现了地质灾害易发性区划的网络化与自动化,最终形成贵州省滑坡灾害易发性区划图.对于单体边坡,通过建立稳定性分析模型库,对其稳定性进行分析.运用可拓学综合评判模型,判断滑坡所处变形阶段,确定预警级别.系统用于路网的规划、公路建设运营以及养护,对防灾减灾有重要意义. [1] 阳岳龙, 龙万学, 杨禹华, 等. 贵州省主要地质灾害危险度区划研究[J].中国安全科学学报, 2008, 18(5):5-10. [2] 裴丽娜, 孔春芳, 刘 刚, 等. 基于 ArcEngine的灾害地质立体图切剖面算法设计与实现[J].华中师范大学学报:自然科学版, 2012, 46(1),109-115. [3] 赵建三, 颜 奇, 徐卓揆, 等. B/S 模式的边坡监测数据分析及安全预警系统设计与实现[J]. 测绘科学, 2010, 3(6):186-188. [4] Fitzner D, Hoffmann J, Klien E. Functional description of geoprocessing services as conjunctive data log queries[J]. Geoinformatica, 2011, 15(1): 191-221. [5] 王卫东, 曾 科, 方理刚. 基于地理处理服务的滑坡敏感性区划研究[J]. 中南大学学报:自然科学版, 2011, 42(7):2086-2094. [6] 王卫东, 陈燕平, 钟 晟. 应用CF和Logistic回归模型编制滑坡危险性区划图[J]. 中南大学学报: 自然科学版, 2009, 40(4): 1127-1133. [7] Yamagishi H. Marui H. Ayalew L. Landslide in Sado Island of Japan: part II. GIS-based susceptibility mapping with comparison of results from two methods and verifications[J]. Engineering geology, 2005, 81(4): 432-445. [8] Shannon C E, Weaver W. The Mathematical Theory of Communication[M]. Urbana :The University of Illinois Press, 1947. [9] Stephen D B. Detecting group differences: mining contrast sets[J]. Data Mining and Knowledge Discovery, 2001(5): 213-246. [10] 郑颖人, 时卫民, 杨明成. 不平衡推力法与Sarma法的讨论[J]. 岩石力学与工程学报, 2004(17): 3030-3036. [11] 陈祖煜. 土质边坡稳定性分析-原理、方法、程序[M]. 北京:中国水利水电出版社, 2003. [12] 蒋 鑫, 凌建明, 谭 炜. 高速公路填砂路基边坡稳定性分析[J]. 铁道工程学报, 2008(9): 1-6. [13] 徐峻龄, 廖晓平, 李荷生. 黄茨大型滑坡的预报及其理论和方法[J]. 铁道工程学报, 1996(2): 197-205. Research on GIS-based highway slope risk analysis and early warning system WANG Weidong1,2, LIU Chao1, LI Dahui1, TAN Hanhua3, LUO Qiang4, LONG Wanxue3 (1. School of Civil Engineering, Central South University, Changsha 410075;2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075;3.Guizhou Transportation Planning Survey and Design Academe CO. LTD., Guiyang 550081;4.Guizhou Provincial Department of Transportation, Guiyang 550003) To research on the landslide susceptibility mapping, a Subjective and Objective Weighting Method-based landslides susceptibility mapping GP model was established. The model was based on the landslide susceptibility mapping research system and formed with six disaster-induced factors (elevation, slope, lithology, geological structure, railway construction and average anural rainfall) and their secondary indexes. This model was published as a web service which can draw landslides susceptibility map automatically in WebGIS while called. To study the individual slope, the instability risk was predicted by analyzing and calculating the landslides stability with geological mechanic methods. Then according to the monitoring data, the deformation stage can be judged and the warning level of landslide can be determined with the prediction models. In summary, we conbined the geological hazard macroscopic mapping and individual slope stability analysis with monitoring and warning and applied them to the highway slope information management system in this paper, which will successfully analyze the highway slope risk and warn the hazard. slope information management; risk assessment; geo-hazard susceptibility mapping; stability analysis; monitoring and prediction 2015-01-11. 国家自然科学基金项目(51478483);交通运输部科技项目 (2003353352480) . 1000-1190(2015)03-0452-08 P642.22 A *E-mail: 147745@163.com.4 重点边坡监测管理分析与预测预报



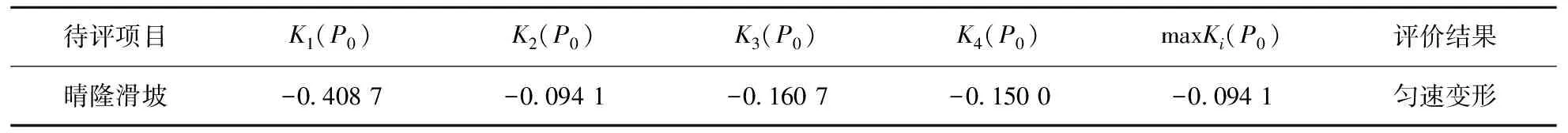
5 结语
