整体分析法在中学化学教学中的作用探究
2015-03-21李建雄,丁永萍,郭玉玮等
整体分析法在中学化学教学中的作用探究
李建雄1,丁永萍2, 郭玉玮2,谷中明2*
(包头师范学院1.继续教育学院,2.化学学院, 内蒙古 包头 014030)
摘要:针对千奇百怪的化学问题,化学教学也是方法多变的,可是越来越多的方法不适应问题的解决,所以方法的探究就成了现在的教学中最大的难题。整体分析法是一种综合的逻辑思维方法,很多化学问题用整体分析法更容易解决,思路更清晰。如氧化还原问题、离子反应问题、化学平衡等问题。教师应用整体分析法进行教学,能让同学们的解题思路更加清晰,看待问题更全面,可以调动同学们的探索思维,使其更好的挖掘教材中的探索性问题,是化学问题的解决方便、快捷。
关键词:整体分析法;化学教学;思维;应用
面对化学教学,令所有教师为难的不在内容而在于方法,合理的教学方法使很多较为复杂的化学问题变得简单清晰。随着化学问题的多样化,教学方法变得尤为重要,也是每位教学工作者较为关注,精心设计教学内容是教学中重要环节。讲授技巧是和上课的互动教学是息息相关的,而教学的互动与教学的内容联系在一起的,教学内容的变化使教学方法不断变化,教育内容、教育内容和教学活动的革新需要相应的教学方法配合[1-3]。 目前针对化学问题的解决方法有很多,对整体分析法的研究是比较突出的,有选择从质量守恒这个整体出发的,有选择从实验方面入手的,选择的角度各异,但是目的相同,均是突出整体分析法解题的优势[4-6]。那么如何使整体分析法应用于更多的化学问题,通过本文的介绍我们来着重了解一下整体分析法解决化学问题。
1整体分析法与氧化还原问题
氧化还原问题中最重要的规律具有守恒性,整个过程化合价升降的总数相等,得电子和失电子数一样,正负电荷也守恒,个元素原子个数相等。而其中的几个守恒关系所能应用的就是整体分析,听过对整体情况的分析来判断是否守恒。
我们经常遇到的氧化还原问题是有关于连续反应的,就如A﹢B→C﹢D,C﹢E→G﹢F,这样的反应中物质完成了一次循环,相互之间因为电子的得失达到了一个动态的守恒[7]。分析整体电子转移而言,将化学的变化看作整体,从整体考虑分析试题,简单化,解题快。
例1:元素化合价问题[8]
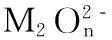
解析:根据题意可知,解此题依据的化合价升降总数相等,有方程式

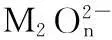
例2:得失电子问题
将0.64 g Cu加入浓硝酸中,产生混合气体体积0.009 mol(含NO、NO2和N2O4),且反应掉浓硝酸0.032 mol。产生的气体和空气混合,用NaOH吸收氮氧化物,生成NaNO2和H2O。计算大气中反应掉O2在标况下体积为多少毫升?
解析:整体分析题意可有
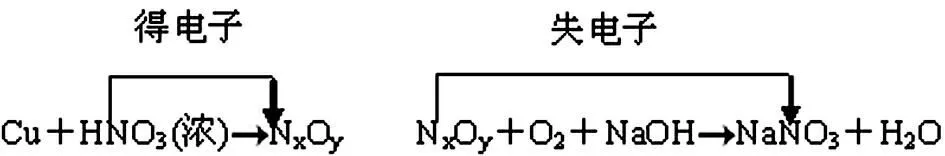
根据题意知NxOy是HNO3得电子数和产生NaNO3时NxOy失电子数相等,那么,Cu失电子数与O2得电子数必须相等,且Cu与O2关系:2Cu~O2,n(Cu)=0.01 mol,n(O2)=0.005mol,V=112 mL。
上述就是整体分析法在氧化还原问题中的部分应用实例,整体分析电子转移在硝酸与氮氧化物之间,一是Cu失电子数与HNO3得电子数相等。同样的道理得出结果。不难看出把几步反应综合起来考虑,可以省去很多不必要的麻烦,更容易理解。
2整体分析法与离子反应问题
离子反应问题中,经常用来考验大家的是离子方程式的正误,而判断正误中经常被我们忽略的就是电荷守恒问题,同学经常把注意力放在离子共存上,而不知道电荷守恒也是离子反应问题的关键问题,氧化还原反应也是贯穿离子反应始终的。
例题:下列表示对化学反应的离子方程式正确的是()
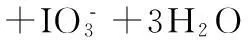
B、向NH4HCO3溶液中加过量的NaOH溶液并加热:


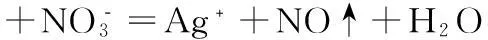
解析:正确的答案是C项。
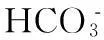
3整体分析法与盐类水解问题
盐类水解实质是弱酸根离子结合H﹢或弱碱阳离子结合OH﹣,破坏水的电离平衡,促进水的电解。由于水解的是弱酸和弱碱,其中很多都是分很多步骤进行的,有些甚至还是双水解,一涉及到多步反应,我们就会用到整体分析法。而且盐类水解问题常常结合离子反应问题,会涉及到电荷守恒、物料守恒、质子守恒,甚至将其中的两者结合起来解题,所以整体分析法也常被应用与盐类水解问题,很多时候我们只是需要一个整体过程,所以那中间的部分就会对我们的分析起到一定的阻碍作用,而此时用整体分析法便可以将阻碍度降到最低,便于我们快速解题。下面我们用框图来明确一下整体分析法与解题的关系(见图1)。
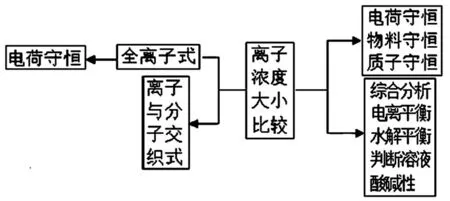
图1
例题:下列溶液中微粒的物质的量浓度关系正确的是()[9]
A、室温下,向0.01mol·L﹣1NH4HSO4溶液中滴加NaOH溶液至中性:
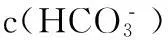

D、25℃时,pH=4.75、浓度均为0.1mol·L﹣1的CH3COOH、CH3COONa混合液:c(CH3COO﹣)+c(OH﹣)﹤c(CH3COOH)+c(H﹢)
解析:正确答案是A项
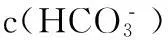

D项根据物料守恒c(Na+)=0.5c(CH3COOH)+0.5c(CH3COO﹣)及电荷守恒c(Na﹢)+c(H﹢)=c(CH3COO﹣)+c(OH﹣),仅能得出c(CH3COO﹣)+2c(OH﹣)=c(CH3COOH)+2c(H﹢)。
4整体分析法与求混合气体平均分子量问题
例题:丁烷完全裂解为乙烯与乙烷和丙烯与甲烷,产生气体的平均分子量为多少[9]?
解析:选用一般方法分析这个问题是比较困难,因而会觉得无从下手。就比如若用加权平均法,因为气体的摩尔百分数无法知道,就会觉得无法继续计算。
那如果我们换个角度思考一下,1.0 mol丁烷分解得到混合气一定还是1.0 mol的量,即58克,裂解过程两次反应均为1.0 mol生成2.0 mol气体的反应,即

图2
无论裂解过程两反应比例如何,1.0 mol丁烷生成的混合气体一定为2.0 mol,那么很简单的我们就可以得出平均分子量为:58÷2=29
5整体分析法与多步反应问题
多步反应问题中涉及到的是整体的质量的守恒,关系到多步反应,那必然从始态到终态会有几步甚至多步反应,也就是说过程是复杂的。即A+X=B+Y,C+Y=D+Z。但
是,往往我们要的结果和其中的过程关系不大,也就是说我们只想知道生成的Z与A的关系,所以,我们就只要对整体进行系统的分析即可,只要找到它们的潜在关系,过程是可以忽略的。
例1:14 g Fe粉与10 g S粉混合,真空加热反应后将固体投入足量HCl,最后气体的体积是?[10]
解析:判断铁过量,起初是算出余Fe和生成FeS量,利用反应式得出它们和HCl反应后,H2和H2S的质量,然后得出气体总量。
对比分析,解题过程是整体分析法:在判断铁过量,分析各步反应的数量无关紧要,而是分析反应物(Fe、S、HCI);终态有哪些反应物(FeCI2、H2S、H2)。然后利用整体的总质量守恒列式,对比发现,整体法的优点:简明、易于理解、快捷及方便。
设最终气体质量为x克,有:14+10+14÷56×2×36.5=14÷56×127+x,得x=10.5 (g)
例2:向含有1.0 mol HCI和1.0 mo lMgSO4混合液中加1mol·L﹣1Ba(OH)2溶液,产生沉淀物质的量(n)与加入Ba(OH)2溶液体积(V)间的关系图正确的是()(见图3)。

图3
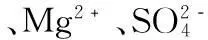
根据题意不难发现,该过程是个多步反应问题,分析有三个阶段
第一个阶段,根据H﹢和Mg2﹢的性质,与OH﹣离子的反应顺序是
H﹢>Mg2﹢,就相当于先有H2SO4生成,故可有反应

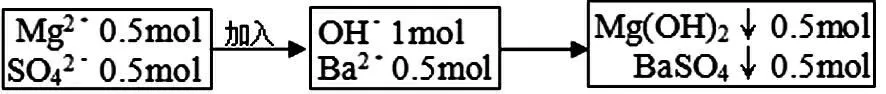
由反应知道,总共生成的沉淀是1mol,加入的体积是0.5L:
第三个阶段,分析整个试题可知,反应中还存在MgCl20.5mol,则有

再继续加入Ba(OH)2也不会有沉淀生成了,故有明显反应发生的就是这三个阶段,那么,结合分析不难找出答案,答案是D选项。
该题中应用的是整体物质的量守恒,并且只有对题目进行系统的、整体的分析,才可以寻找到突破,解出正确答案。
例3:Cu和Cu2O的混合物7 .6g与足量的稀硝酸反应,产生NO气体再标准状况下体为1.12L,向所得溶液中加入足量的NaOH溶液,产生的沉淀经过滤、洗涤、干燥、灼烧后,得到黑色固体的质量是()
A.8 .8gB.9 .2gC.8gD.16g
解析:看到这个题目,我们最原始的思路是
n(NO)=V∕Vm=1.12L÷22.4L∕mol=0.05mol,并且有反应方程式
3Cu+8HNO3=3Cu(NO)2+2NO↑+4H2O,
3Cu2O+14HNO3=6Cu(NO3)2+2NO↑+7H2O
设混合物中铜的物质的量为x,氧化亚铜的物质的量为y,则有

并且,在灼烧的时候氢氧化铜会变成氧化铜,此时物质的量守恒,则生成的氧化铜中铜的物质的量与原混合物中铜物质的量守恒,所以黑色固体的质量为(0.04+0.06)mol×80g/mol=8.8g
如果我们换个角度去解答,运用整体分析法解决这个问题,会有什么效果呢,下面我们来看一下:
首先进行整个过程的大体分析,用表格来系统阐述一下,

其中生成的NO的物质的量是n(NO)=1.12L÷22.4L/mol=0.05mol,此时根据电子守恒,硝酸中氮得到的电子总数也就是铜失去的电子总数,即n(e﹣)=0.15mol,而铜失去的电子与氧原子得到的电子仍旧是守恒的,所以有n(O)=0.075mol,此时氧的增加量就是m(O)=1.2g,而氧的增加量就是铜的转移量,那么最终的黑色固体的量为m(CuO)=7.6+1.2=8.8g,故答案很明显是A。
从上面的对比不难看出,整体分析法的解题过程更加简洁明确,容易理解,更加节省了我们的解题时间,突出了整体分析的优越性。
6整体分析法与电化学问题
电化学问题是由氧化还原和水解、电解综合起来的一类习题,涉及到的知识内容比较广泛,那么解题方法也是与这几类问题的解法相近的,基本方法概括为三类:根据电子守恒法计算、根据总方程式计算(考虑的总反应式的比例)、根据关系式计算(依据得失电子守恒定律),由此不难看出,整体分析是必不可少用的[10]。
例:用惰性电极电解一定浓度的硫酸铜溶液,通电一段时间后,向所得的溶液中加入0.1molCu2(OH)2CO3后恰好恢复到电解前的浓度和pH值(不考虑二氧化碳的溶解)。则电解过程中共转移的电子数为多少[11]?
解析:加入的物质是Cu2(OH)2CO3,要是电解后溶液复原,必然涉及两个反应:,
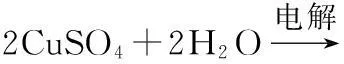

加入0.1molCu2(OH)2CO3,这就相当于电解出0.2molCu后再单独电解0.1molH2O,根据氧化还原反应中电子得失关系,转移电子总数为:0.1mol×2+0.2mol×2=0.6mol。
7结论
整体分析法对我们化学教学影响重大,对于学生的学习也是意义非凡的。通过整体分析法使我们的课堂更加完善,学习效率更高。而且,对于该方法的深入理解,可以锻炼学生的思维能力,拓展发散思维。整体分析法是一种重要的逻辑思维方法,而逻辑思维的培养需要平时的日积月累,所以要想充分掌握并运用整体分析法,重要的就是多做,多思。现代的学习理论告诉我们,知识的学习或表征,只有做到条件化、结构化、策略化、整体化,才能有效的用来创造性的解决问题[13]。所以,合理的整体分析,合理的运用,合理的逻辑思维,有利于提高教学质量,提高学习效率,更有利于我们进一步对中学化学教学进行探究。
〔参考文献〕
[1]刘知新.化学教学论[M].北京:高等教育出版社,2009.
[2]刘知新.化学学习论[M].南宁:广西教育出版社,1996.
[3]王后雄.化学方法论[M].长沙:中南大学出版社,2003.
[4]刘宇.谈整体分析法解决化学问题[J].数理化学习(高中版),2010(04)..
[5]周仁鸽.论化学课堂的整体构建[J].化学教学,2012,(08).
[6]刘知新,王祖浩.化学教学系统论[M].南宁:广西教育出版社,1995.
[7]罗滨.对化学教学教学方法的认识[J].化学教育,1998.(6).
[8]罗伟.学科专业知识·中学化学[M].北京:首都师范大学出版社,2010.
[9]王后雄.高考完全解读:课标版.化学[M].南宁:接力出版社,2012.
[10]黄爱民.整体分析法在中学化学解题中的应用[J].化学教学,1994,(05).
[11]曲一线.5年高考3年模拟.化学[M].北京:首都师范大学出版社,2005.
[12]人民教育出版社化学室编著.化学[M].北京:人民教育出版社,2003.
[13]解守宗.中学化学教学与实践研究[M].北京:高等教育出版社,2003.
The Role of Overall Analysis in Middle School Chemistry Teaching
LI Jian-xiong1,DING Yong-ping2, GUO Yu-wei2, GU Zhong-ming2*
(1.Faculty of Continuing Education,2.Faculty of Chemistry,Baotou Teachers College,Baotou 014030)
Abstract:In view of the strange chemical problems, chemistry teaching method is changeful, but more and more of the method is not adapted to the solution of the problem, so the method of exploration becomes the biggest problem in the present teaching.Overall analysis is a kind of comprehensive method of logical thinking, many chemical problems in overall analysis easier to solve, to think more clearly.Such as redox, ionic reaction, chemical equilibrium, the solution of the problem.Teachers teaching overall analysis method, the overall analysis can let students' problem solving ideas more clear look, the more comprehensive, the overall analysis can arouse students' exploring thinking, analysis method can make students as a whole better excavating exploratory problem in teaching materials, the overall analysis method to make chemical solution convenient and quick.
Key words:the overall analysis; chemistry teaching; thinking; application
中图分类号:G633.8
文献标识码:A
文章编号:1004-1869(2015)02-0102-05
作者简介:李建雄(1962-),内蒙古五原县人,实验师,研究方向:大学化学实验,成人教育。
基金项目:包头师范学院教改课题, 包头市科技计划项目(2012S2005-5-27)。
收稿日期:2014-12-17
