基于奇异值分解的PCNN 红外与可见光图像融合

陈广秋，高印寒，段 锦，韩泽宇，才 华

（1.吉林大学 仪器科学与电气工程学院，吉林 长春130061；2.吉林大学 汽车仿真与控制国家重点实验室，吉林 长春130022；3.长春理工大学 电子信息工程学院，吉林 长春130022）

1 引 言

红外与可见光是两类不同模态的传感器，红外传感器通过探测物体自身的热辐射产生图像，能够显示隐藏的热目标，且受外界干扰因素影响较小，但图像对比度较低，目标与场景的细节反映能力差，不符合人的视觉习惯；可见光成像传感器是通过捕获物体的反射光产生图像，具有高分辨率的细节信息，但易受天气、烟雾、照度等因素影响，不能全天候工作。将两者结合使用，相互取长补短便可以发挥各自的优势，提高图像的质量，改善人们的视觉效果，增加图像中的信息量及可靠性，显现出目标更加全面的特性，为决策者提供更可靠、更准确的分析结果。因此，红外与可见光图像融合在军事和安全监控等领域有着广泛的应用。

根据图像处理域的不同，目前图像融合算法主要分两类：基于空间域的融合算法和基于变换域的融合算法［1］。前者是直接在图像的像素灰度空间利用一定的算法进行融合；主要有加权、主成分分析（PCA）、HIS 变换和神经网络等算法；后者是先对源图像进行变换，然后再对变换得到的系数利用各种融合策略进行组合，得到融合图像的变换系数，最后通过逆变换得到融合图像；主要包括各种金字塔、小波、Curvelet、Controulet等变换。由于多尺度变换具有空频域分析图像的能力成为变换域图像融合常用的方法及研究热点［2－4］。对空间域的融合算法，在图像融合发展早期研究较多［5－8］，近年来对其研究较少。但基于空间域的融合算法复杂度低，便于硬件实施［9－10］，融合效果可以通过优化算法进行提高。另外，多数空间域融合算法可以直接应用到变换域作为变换系数的融合策略，尤其近年来，研究多尺度与脉冲耦合神经网络（Pulse Coupled Neural Networks，PCNN）结合的相关融合算法逐渐升温［11－12］，所以有必要对空间域基于PCNN 的融合算法作进一步研究，以提高融合精度，同时为多尺度分解及硬件实施提供一种新算法。

脉冲耦合神经网络（PCNN）是第三代人工神经网络的新模型，因具有同步激发、变阈值等特性而被应用到图像融合领域。在使用PCNN进行图像融合的大部分文献中，神经元的链接强度都是通过经验或实验选择的一个常数。但人眼视觉系统对图像中不同特征区域反应的强烈程度是有差异的，即视觉皮层中不同神经元耦合具有差异性，这种差异性体现在PCNN 中就是各神经元的链接强度的不同。因此，PCNN中链接强度与图像中该点像素处的特征信息是密切相关的。图像矩阵的奇异值是一种性质良好的代数特征，集中了图像的能量，包含了图像的绝大部分结构信息，能够反映图像的区域特征，符合人眼的视觉处理机制。本文提出了一种基于局部区域奇异值分解的PCNN 图像融合策略。利用局部区域奇异值构造局部结构信息因子，作为PCNN 对应神经元的链接强度，自适应调整局部结构信息因子值来表征图像特征的变化，通过PCNN 运算得到能够反映单点像素及其邻域整体像素特征的点火映射图，有效提取图像中的目标与背景信息，最后通过选择性融合规则得到融合图像，使融合图像更符合人的视觉系统。

2 算法的基本原理

2.1 PCNN 基本原理和简化模型

PCNN 是由若干个神经元互相链接形成的一种动态非线性反馈网络模型，包括接收域、调制域和脉冲产生器3部分。最初基于哺乳动物视觉系统的PCNN 模型极为复杂［13］，大量的文献对其进行了改进与简化。本文采用最常使用的离散数学迭代模型［14］，如图1所示。

其数学方程描述为

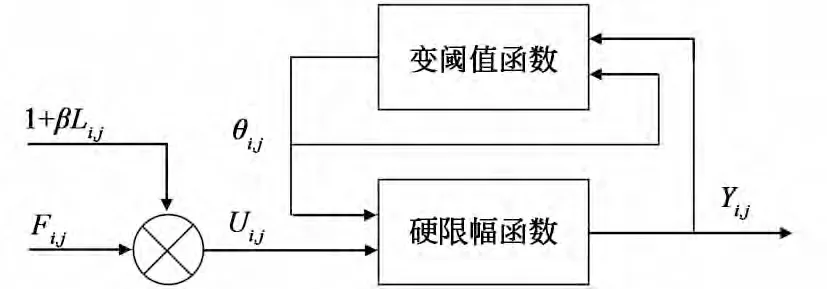
图1 PCNN 神经元简化模型Fig.1 Simplified model of PCNN neuron

其中：下标（i，j）是神经元的标号；Fij（n）是神经元在第n次迭代时的反馈输入；Iij为外部输入刺激信号，通常为像素点（i，j）的灰度值；Lij（n）是神经元的链接输入；βij是链接强度；Uij（n）是神经元的内部活动项；Yij（n）则是第n 次迭代时（i，j）神经元的输出；W 为神经元之间的链接权系数矩阵，VL是链接输入的放大系数；θij和Vθ是变阈值函数输出和阈值放大系数；αL和αθ分别为链接输入和变阈值函数的时间常数；n 表示迭代次数。如果Uij（n）＞θij，则神经元产生一个脉冲，称为一次点火。n次迭代以后，利用（i，j）神经元总的点火次数来表示图像对应点处的信息。经过PCNN点火，由神经元总的点火次数构成的点火映射图作为PCNN 的输出。

2.2 图像的奇异值分解及其特性

奇异值分解（Singular Value Decomposition，SVD）为提取图像的代数特征提供了新的方法，在数据压缩、信号处理和模式识别等领域获得了广泛应用。奇异值分解定理及其特性可详细描述如下［15－16］：

若矩阵A∈Rm×n，则存在两个正交矩阵U＝［u1，u1，…，um］∈Rm×m，V＝［v1，v2，…，vn］∈Rn×n以及对角阵S＝diag［σ1，σ2，…，σp］，其中UTU＝I，VTV＝I，p＝min（m，n），σ1σ2≥…≥σp＞0使得式（6）成立：

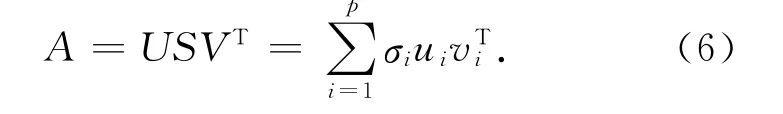
式（6）称为矩阵A 的奇异值分解，S 称为奇异值矩阵，σi（i＝1，2，…，p）为矩阵A 的奇异值，矩阵的奇异值表现的是图像的本质特性而不是视觉特性，反映了图像的内在属性。矩阵A 的能量E可 表 示 为E ＝‖A ‖2F，结 合 式（6），可 证明E＝‖A‖2F＝‖S‖2F：

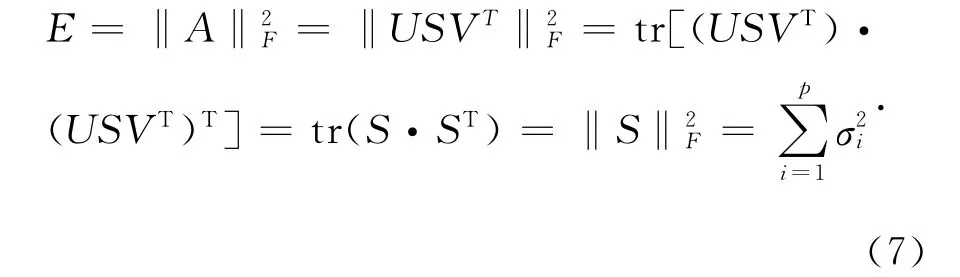
由式（7）可以看出，图像A 经过奇异值分解后，能量信息集中于奇异值矩阵S 中，换言之，图像的奇异值代表了图像的能量特征。文献［17］对SVD 作了进一步研究，对图像2（a）做奇异值分解，重构时，将奇异值向量替换为同样大小的单位对角矩阵，得出图2（b）。

图2 剥除奇异值之后的残差图像Fig.2 Different image after removed singular value

由图2（b）可看出，剥除奇异值向量后，图像的结构信息几乎完全被屏蔽，由此可见，图像的奇异值向量包含了图像的绝大部分结构信息，奇异值越大，包含的结构信息越丰富，在图像处理领域引入奇异值分解概念是对图像特征提取的一大应用，这也是本文算法的理论基础。

图像的奇异值具有以下特性：（1）稳定性；奇异值的变化不大于扰动矩阵的2范数。这就意味着图像的奇异值特征对图像噪声、图像光照条件等不同引起的变化具有不敏感的特性；（2）旋转位移不变性；即对图像进行旋转运算或是作行或列的置换运算时，图像的奇异值特征不变。意味图像奇异值能有效地反映图像的内在属性，保证了奇异值特征衡量图像质量的鲁棒性。

2.3 自适应链接强度的确定

基于传统PCNN 的图像融合算法中，神经元的链接强度是根据经验或实验选择的一个常数。但根据人眼视觉处理机制，视觉系统对图像中不同特征区域的反应的强烈程度是有差异的，即视觉皮层中不同神经元耦合具有差异性，这种差异性体现在PCNN 中就是神经元的链接强度系数的不同。从PCNN 数学描述方程中的内部活动项可看出，输入源图像的明显特征部分在最后融合图像中所占权重与链接强度β值的大小有关。所以有理由认为链接强度β值应随图像特征的变化而改变，以此来表征图像不同区域的特征信息，而不应是一个常数。这样可以有效地提取图像细节信息。空间域内构造PCNN 链接强度具有代表性的研究成果如文献［18］～［20］。文献［18］利用局域对比度得到对应像素点的链接强度值；文献［19］利用局域拉普拉斯能量和局域标准差构造对应像素点的链接强度值；文献［20］利用邻域空间频域作为神经元激励，改进的拉普拉斯能量和作为链接强度值。这3种算法针对多聚焦或医学图像的融合都取得了较好的效果，但对光谱差异较大的红外与可见光图像，链接强度值的稳定性会下降，容易造成融合图像的不连续和边缘模糊等缺陷。

图像的奇异值包含了图像的结构信息，集中了图像的能量信息。文献［21］利用两幅图像块奇异值差值的均值来表征灰度图像结构信息的丢失程度；文献［22］利用两幅图像块奇异值差的加权均值与剥除奇异值之后的残差图像信息作为压缩图像质量评价测度；上述文献说明用局部区域奇异值来表征图像的特征变化是可行的。文献［23］利用梯度域局部区域奇异值和来区分图像的平坦区域和非平坦区域，且具有较好的抗噪能力，但这种方法不能表征图像平坦区域的特征变化与非平坦区域的结构纹理信息变化，不适合作为PCNN中的链接强度值；受上述文献启发，参照文献［23］的构造方法，本文利用局部区域奇异值的均值定义一个局部结构信息因子，来表征单幅图像局部区域的内容及特征变化：

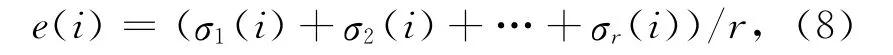
式中σ1，σ2，…σr为局部区域内的奇异值，e 值的大小体现了图像局部区域内基本结构模式，体现局部区域包含细节信息的丰富程度，能够表述图像特征的变化。本文融合算法中采用局部结构信息因子作为PCNN 中的链接强度值，表征图像不同区域的特征信息。

2.4 基于块奇异值分解的PCNN 融合算法

利用局部结构信息因子值作为PCNN 对应神经元的链接强度值，同时像素灰度值激励每个神经元，再经过PCNN 点火获得参与融合图像的每个特征对应的点火映射图，最后根据比较选择算子来确定融合图像。图3 以两幅图像的融合为例说明基于奇异值分解的自适应PCNN 图像融合过程。

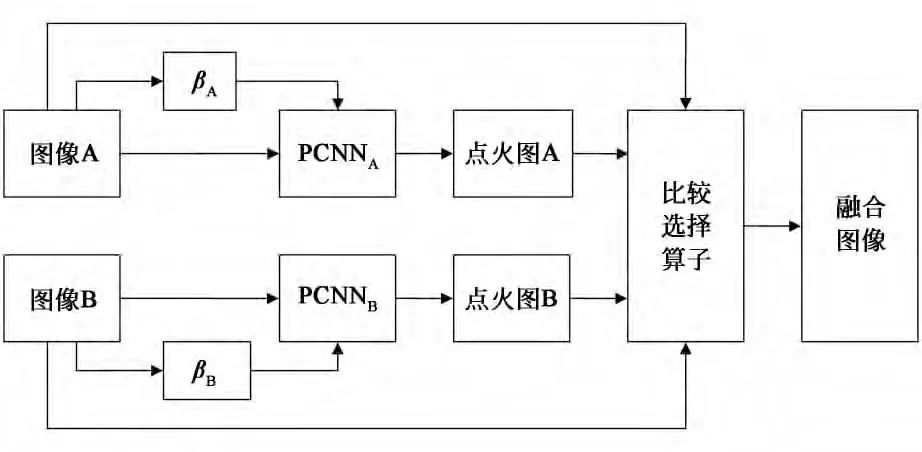
图3 PCNN 图像融合框图Fig.3 Schematic diagram of PCNN－based fusion algorithm

算法步骤：

（1）对待融合的两幅图像（M×N）进行归一化处理，分别记为A 和B （可推广到多幅）。令A作为第1个神经网络PCNNA中各神经元的反馈输入，B 作为第2 个神经网络PCNNB中各神经元的反馈输入。

（2）对矩阵A 和B 进行滑动窗口平移分块，块的大 小为k×k，中心点为（i，j），共分M×N 个子块，分别计算出各子块图像的奇异值，利用公式（8）计算局部结构信息因子eA（i）和eB（i），形成大小为M×N 的矩阵，其元素值即为对应的链接强度βij值，得到A、B 中 每个像素对应的βA，ij、βB，ij值，i＝1，2，…，M，j＝1，2，…，N。

（3）初始值分别设为：Lij（0）＝Uij（0）＝0，θij（0）＝1， 此时所有的神经元都处在熄火状态，即Yij（0）＝0，脉冲数Tij（0）＝0。

（4）根据式（1）、（2）、（3）、（4）、（5）计算Lij（n）、Uij（n）、θij（n）和Yij（n）。

（5）累计神经网络每次迭代运行的输出：Tij（n）＝Tij（n－1）＋Yij（n）。

（6）判断n 值是否为Nmax（最大迭代次数），如果n＜Nmax，重复步骤（5）～（6），如果n＝Nmax，迭代运算结束。输出点火图OA和OB。

H（i，j）为融合后的像素值。经过PCNN 处理后，每幅参与融合的图像得到各自对应的点火映射图，通过比较点火映射图中相应像素的点火频数，数值越大，表明图像在该处的信息越丰富，融合时应选择该点像素，所以上述融合过程可有效提取图像边缘、纹理等信息。

3 实验与结果分析

通过3 步实验来验证本文融合算法的有效性。

第一步，将本文算法与常用的典型多尺度分解融合方法进行比较；第二步，本文算法与典型的空间域内基于PCNN 的融合算法进行比较；第三步，本文算法与其他融合算法对噪声图像的融合效果进行比较；通过视觉观察对融合结果进行主观评价。第一步和第二步融合结果的客观评价采用互信息MI［24］、结构相似度SSIM［25］和边缘信息传递量QAB／F［26］3种指标；由于待融合图像含有噪声，所以第三步融合结果的客观评价采用信息熵（ENTROPY）［27］、估计信噪比（ESNR）［28］和清晰度（DEFINITION）［29］3种指标；本文融合算法中链接强度β值可通过计算3×3矩阵的结构信息因子得到，PCNN 中其他参数根据经验进行设置，为体现公平性，本文的其他参数与文献［18］～［20］中设置相同。每个神经元与其周围3×3邻域内的神经元相链接即p×q＝3×3，3×3链接核矩阵为：

3.1 本文算法与多尺度分解方法融合效果的比较

为了验证本文融合算法能够有效提取图像边缘、纹理等细节信息，同时保留源图像的亮度和对比度等信息。分别应用Contrast pyramid、Gradient pyramid、Laplacian pyramid、DWT、SIDWT、Curvelet、Contourlet和本文算法对图4（a）（b）所示的红外与可见光图像进行融合实验。多尺度分解中低频系数采用等权值平均，高频系数采用绝对值取大融合规则。融合结果如图4（c）～（j）所示，客观评价指标如表1所示。

图4 本文算法与多尺度分解方法的融合结果Fig.4 Fusion results of proposed algorithm and multi－scale decomposition methods

从图4中可以看出，图（j）相对于塔式分解、小波、Curvelet、Contourlet变换方法的融合图像更清晰、自然，对比度适中，细节丰富，具有良好的视觉效果。这表明本文的融合算法能够最大限度地提取源图像细节，保留源图像的亮度和对比度信息。从表1中的数据可以看到，本文融合算法的客观评价均为最优，与主观评价一致，进一步证明了本文融合算法的有效性。

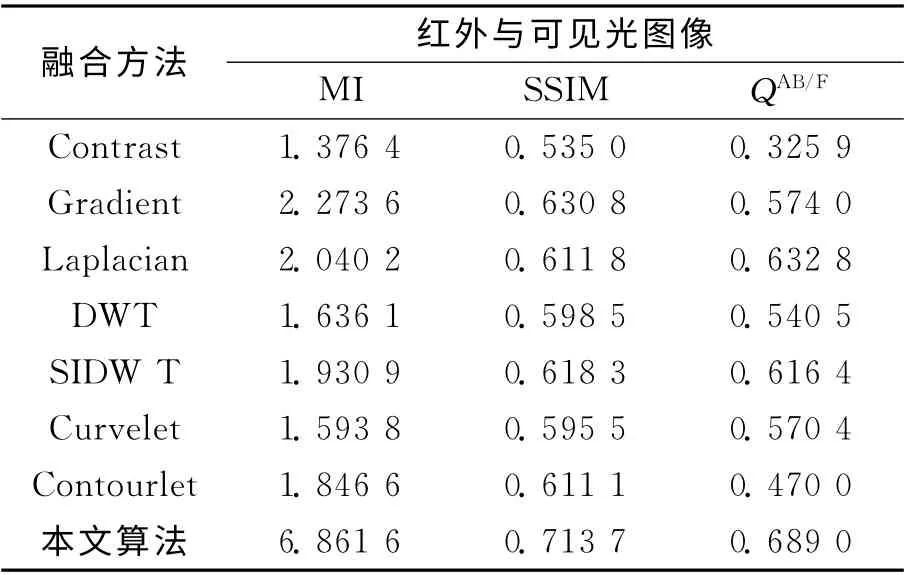
表1 本文算法与多尺度分解方法融合结果的比较Tab.1 Fusion results comparison of proposed algorithm and multi－scale decomposition methods

3.2 不同PCNN 方法融合结果的比较

为了验证局部区域奇异值分解得到的局部结构信息因子作为链接强度在PCNN 方法中的优越性，在空间域内，分别应用传统PCNN（链接强度β＝0.2）、文献［18］、文献［19］、文献［20］和本文算法对图5（a）（b）红外与可见光图像进行融合实验，融合结果如图5（c）～（g）所示，客观评价指标数据如表2所示。

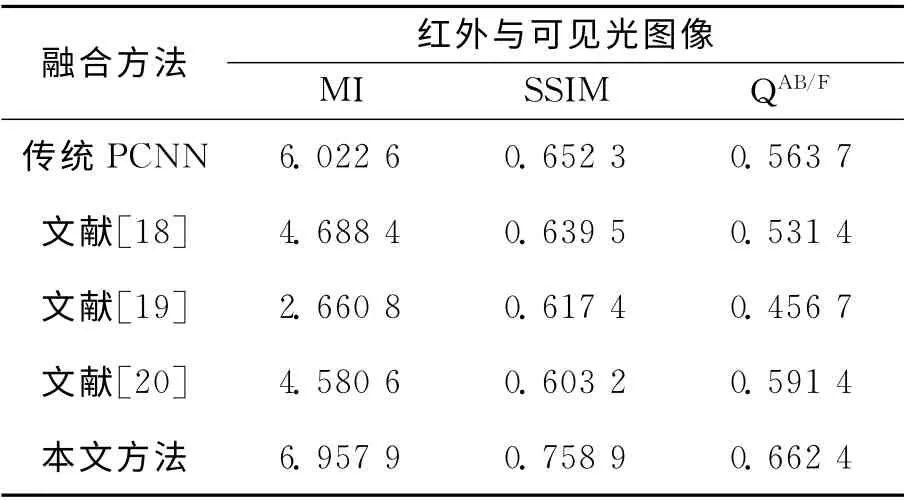
表2 不同PCNN 方法融合结果的比较Tab.2 Fusion results comparison of different PCNN methods

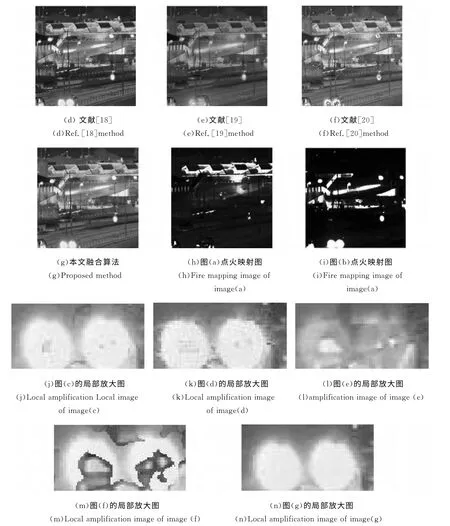
图5 不同PCNN 方法的融合结果Fig.5 Fusion results using different PCNN methods

从图5中可以发现，在图（g）中，路灯下的人、路上行驶的车辆、屋顶等目标都清晰可见，图像对比度适中，边缘刻画准确，相对于（c）、（d）、（e）及（f）有更好的视觉效果，这表明应用本文算法能够更好地提取目标信息，最大限度提取源图像中的结构细节和保留源图像亮度信息。从（j）（k）（l）（m）（n）局部放大图可以看到，本文算法的融合图像中没有出现不连续现象。图（h）（i）的点火映射图也表明了本文算法的有效性。对图5 分析可知，应用本文算法融合的图像更能体现源图像的细节信息，保证了图像的整体清晰度且保留了源图像中的结构与纹理信息，这是因为本文利用局部区域奇异值构造的区域结构信息因子作为PCNN 中链接强度β 值，能更好地反映像素的特征信息，符合人眼的视觉系统对图像特征变化的处理机制，具有较强的自适应性，通过PCNN 处理后，能够准确地提取红外与可见光图像中的特征明显区域，保留边缘细节丰富区域，消除可能出现的不连续性，使融合后的图像更符合人的视觉。从表2中可以看出，本文提出的融合策略融合的图像客观评价参数为最优，进一步验证了本文算法的有效性。

3.3 噪声图像融合效果的比较

为了验证矩阵奇异值所具有稳定性和旋转位移不变性在图像融合领域的优越性，分别应用传统PCNN、文献［18］、文献［19］、文献［20］、Laplacian pyramid、DWT、SIDWT 和本文算法对图6（a）（b）中含有均值为0、方差0.01的高斯噪声图像进行融合实验。融合结果如图6（c）～（j）所示，客观评价数据如表3所示。

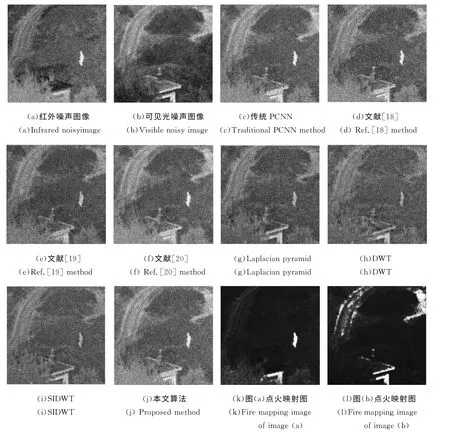
图6 不同融合算法对噪声图像融合的结果Fig.6 Fusion results of noisy images using different methods

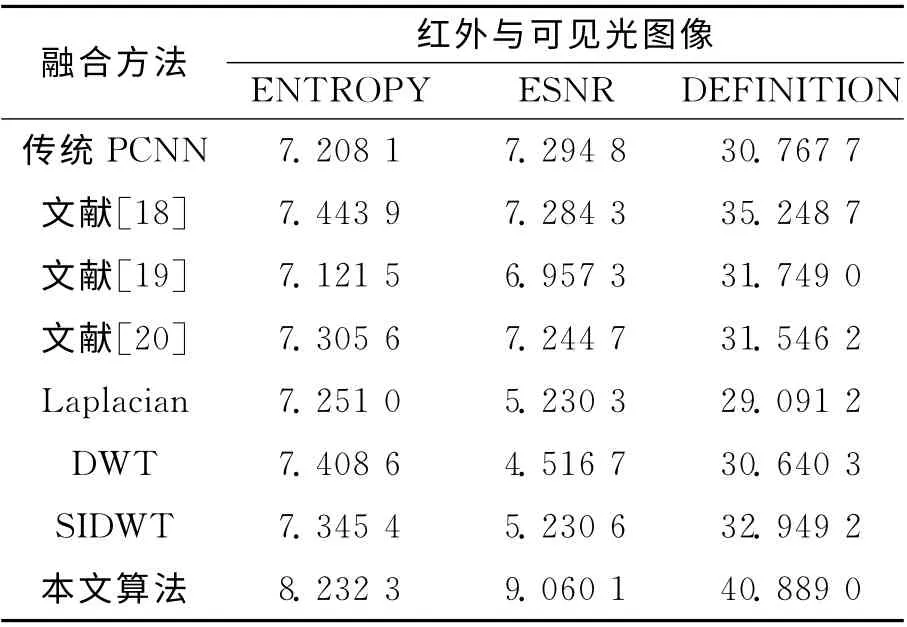
表3 不同融合算法对噪声图像融合结果的比较Tab.3 Fusion results comparison of noisy images using different methods

从图6中发现，在图6（j）中白色的人、栅栏、屋顶等主要目标都清晰可见。这说明矩阵奇异值所具有的稳定性和旋转位移不变性在一定程度上能够消除噪声的影响，使融合图像具有一定的鲁棒性。

4 结 论

针对红外与可见光图像，提出了一种基于局部区域奇异值分解的自适应PCNN 图像融合方法。利用局部区域奇异值构造区域结构信息因子，作为PCNN 对应神经元链接强度值，随着图像特征变化不断地进行自适应调整，通过PCNN 点火处理，得到能够同时反映单个像素特征及其邻域像素整体特征的点火映射图，通过比较选择算子，准确选择明显特征区域，提升红外与可将光图像融合精度。实验结果表明，本文提出的图像融合方法与其他融合方法相比较，能够得到较好的融合效果，具有较强的自适应能力，同时本文算法可以作为多尺度分解的融合策略。

［1］ 才溪.多尺度图像融合理论与方法［M］.电子工业出版社，北京，23014：8－9.Cai Xi.Multiscal Image Fusion：Theory and Method ［M］.Beijing：Publishing House of Electronics Industry，2014：6－9.（in Chinese）

［2］ 陈小林，王延杰.非下采样变换的红外与可见光图像融合［J］.中国光学，2011，4（5）：489－495.Chen X L，Wang Y J.Infrared and visible image fusion based on nonsubsampled Contourlet transform［J］.Chinese Optics，2011，4（5）：489－495.（in Chinese）

［3］ 李光鑫，吴伟平，胡君.红外和彩色可见光图像亮度－对比度传递融合算法［J］.中国光学，2011，4（2）：161－168.Li G X，Wu W P，Hu J.Luminance－contrast transfer based fusion algorithm for infrared and color visible images［J］.Chinese Optics，2011，4（2）：161－168.（in Chinese）

［4］ 唐艳秋，张星祥，李新娥，等.基于人眼视觉灰度识别特性的图像动态范围小波变换处理方法［J］.液晶与显示，2012，27（3）：385－390.Tang Y Q，Zhang X X，Li X E，et al.Image processing method of dynamic range with wavelet transform based on human visual gray recognition characteristics［J］.Chinese Journal of Liquid Crystals and Displays，2012，27（3）：385－390.（in Chinese）

［5］ Burt P J，Kolcznski R.J.Enhanced image capture through fusion［C］.IEEE4th international Conf.on Computer Vision，1993（4）：173－182.

［6］ Jia Y H.Fusion of Landsat TM and SAR images based on principal component analysis［J］.Remote Sensing Technology and Applications，1998，13（1）：46－49.

［7］ Broussard R P，Rogers S K，Oxley M E，et al.Physiologically motivated image fusion for object detection using a pulse coupled neural network［J］.IEEE Transactions on Neural Networks，1999，10（3）：554－563.

［8］ Li S T，Kwork J T，Wang Y N.Multifocus image fusion using artificial networks［J］.Pattern Recognition Letters，2002，23（8）：985－997.

［9］ 范永杰，金伟其，李力，等.基于FPGA 的可见光／红外双通道实时视频融合系统［J］.红外技术，2011，33（5）：257－261.Fan Y J，Jin W Q，Li L，et al.Real time fusion system for visible and IR video based on FPGA［J］.Infrared Technology，2011，33（5）：257－261.（in Chinese）

［10］ 骆媛，金伟其，刘效东.基于颜色查找空间的自然感彩色融合算法及DSP 实时实现［J］.红外与激光工程，2012，41（8）：2241－2246.Luo Y，Jin W Q，Liu X D.Color look－up space based natural color fusion algorithm and DSP real－time implementation［J］.Infrared and Laser Engineering，2012，41（8）：2241－2246.（in Chinese）

［11］ 付朝阳，郭雷，常威威.基于小波变换和多通道脉冲耦合神经网络的高光谱图像融合［J］.吉林大学学报：工学版，2011，41（3）：838－843.Fu Z Y，Guo L，Chang W W.Fusion algorithm of hyperspectral images based on wavelet transform and multichannel PCNN［J］.Journal of JiLin University：Engineering and Technology Edition，2011，41（3）：838－843.（in Chinese）

［12］ 傅瑶，孙雪晨，薛旭成，等.基于非下采样轮廓波变换的全色图像与多光谱图像融合方法研究［J］.液晶与显示，2013，28（3）：429－434.Fu Y，Sun X C，Xue X C，et al.Panchromatic and multispectral image fusion method based on nonsubsampled contourlet transform［J］.Chinese Journal of Liquid Crystals and Displays，2013，28（3）：429－434.（in Chinese）

［13］ Johnson J L，Padgett M L.PCNN models and applications［J］.EEE Transactions on Neural Networks，1999，10（3）：480－498.

［14］ 杨艳春，党建武，王阳萍.基于提升小波变换与自适应PCNN 的医学图像融合方法［J］.计算机辅助设计与图形学学报，2012，24（4）：494－499.Yang Y C，Dang J W，Wang Y P.A medical image fusion method based on lifting wavelet transform and adaptive PCNN［J］.Journal of Computer－Aidcd Dcsign ＆Computer Graphics，2012，24（4）：494－499.（in Chinese）

［15］ 梁毅雄，龚卫国，潘英俊，等.基于奇异值分解的人脸识别方法［J］.光学精密工程，2004，12（5）：543－549.Liang Y X，Gong W G，Pan Y J，et al.Singular value decomposition－based approach for face recognition［J］.Optics and Precision Engineering，2004，12（5）：543－549.（in Chinese）

［16］ 王宇庆.基于图像结构信息复数表示与奇异值分解的灰度图像质量评价方法［J］.光电子·激光，2012，23（9）：1827－1834.Wang Y Q.Image quality assessment based on complex number representation of image structure and singular value decomposition［J］.Journal of Optoelectronics·Laser，2012，23（9）：1827－1834.（in Chinese）

［17］ Aznaveh A M，Azadeh M，Azar F T，et al.Image quality measurement besides distortion type classifying［J］Optical Review，2009，16（1）：30－34.

［18］ 苗启广，王宝树.基于局部对比度的自适应PCNN 图像融合［J］.计算机学报，2008，31（5）：875－880.Miao Q G，Wang B S.A novel image fusion algorithm based on local contrast and adaptive PCNN ［J］.Chinese Journal of Computers，2008，31（5）：875－880.（in Chinese）

［19］ 李美丽，李言俊，王红梅，等.基于自适应脉冲耦合神经网络图像融合新算法［J］.光电子·激光，2010，21（5）：779－782.Li M L，Li Y J，Wang H M，et al.A new image fusion algorithm based on adaptive PCNN［J］.Journal of Optoelectronics·Laser，2010，21（5）：779－782.（in Chinese）

［20］ 夏加星，段先华，魏世超.利用邻域激励的自适应PCNN 进行医学图像融合［J］.计算机应用研究，2011，28（10）：3929－3933.Xia J X，Duan X H，Wei S C.Application of adaptive PCNN based on neighborhood to medical image fusion［J］.Application Research of Computers，2011，28（10）：3929－3933.（in Chinese）

［21］ Shnayderman A，Gusev A，Eskicioglu A M.An SVD based grayscale image quality measure for local and global assessment［J］.IEEE Transactions on Image Processing，2005，14（2）：422－429.

［22］ 张飞艳，谢伟，陈荣元，等.基于视觉加权的奇异值分解压缩图像质量评价测度［J］.电子与信息学报，2010，32（5）：1061－1065.Zhang F Y，Xie W，Chen R Y，et al.Compression image quality assessment based on human visual weight and sin－gular value decomposition［J］.Journal of Electronics ＆Information Technology，2010，32（5）：1061－1065.（in Chinese）

［23］ 许光宇，檀结庆，钟金琴.自适应的有效非局部图像滤波［J］.中国图象图形学报，2012，17（4）：471－479.Xu G Y，Tan J Q，Zhong J Q.Adaptive efficient non－local image filtering［J］.Journal of Image and Graphics，2012，17（4）：471－479.（in Chinese）

［24］ Qu G H，Zhang D L，Yan P F.Information Measure for performance of image fusion［J］.Electronic Letters，2002，38（7）：313－315.

［25］ Wang Z，Bovik A C，Sheik HR，et al.Image quality assessment：from error visibility to structural similarity［J］.IEEE Transactions on Image Processing，2004，13（4）：600－612.

［26］ Xydeas C S.，Petrovi V.Objective image fusion performance measure［J］.Electronics Letters，2000，36（4）：308－309.

［27］ Leung L W，King B，Vohora V，Comparison of image data fusion techniques using entropy and INI［C］.Proc.of 22ndAsian Conference on Remote Sensing，Singapore，2001：152－157.

［28］ 朱博，王新鸿，唐伶俐，等.基于边缘剔除与空间去相关的图像信噪比评估方法研究［J］.遥感技术与应用，2012，27（1）：39－44.Zhu B，Wang X H，Tang L L，et al.SNR estimation for remote sensing images based on edge extraction and spatial dimension decorrelation［J］.Remote Sensing Technology and Application，2012，27（1）：39－44.（in Chinese）

［29］ 李祚林，李晓辉，马灵玲，等.面向无参考图像的清晰度评价方法研究［J］.遥感技术与应用，2011，26（2）：239－246.Li Z L，Li X H，Ma L L，et al.Research of definition assessment based on no－reference digital image quality［J］.Remote sensing Technology and Application，2011，26（2）：239－246.（in Chinese）