双区次临界系统的单群Feynman-α 方程的解析解

王子冠，沈 峰

（国核（北京）科学技术研究院有限公司，北京 102209）

Feynman-α方法是中子噪声分析方法的一种，由Feynman等［1］首先提出，并用来测量增殖系统的反应性。近年来这种方法又被重新研究，并用于ADS 等核能系统次临界度的在线监测［2-3］，也有研究将这种技术应用到核保障中，用于快速检测货物中是否存在铀和钚等其他可裂变元素［4-5］。传统的Feynman-α方法基于单群点堆模型，且未考虑缓发中子的影响。但次临界系统和ADS等核能系统通常由堆芯和反射层构成，并将中子探测器放置于反射层内。对于这类带有反射层的次临界系统，基于单群点堆模型的Feynman-α 方法对其物理特性的描述不够精确。基于此，本文构建基于双区模型的单群Feynman-α方程，并采用构建生成函数的方法推导其解析解，求得中子探测器计数的方差-平均值比值随探测器计数时间变化的关系。

1 Feynman-α 方法

1.1 基本原理

Feynman-α 方法又被称为方差-平均值比方法，它通过分析增殖介质内中子探测器计数的方差-平均值比值随不同探测时间窗长度变化的规律，计算次临界系统的α 本征值和反应性等参数。对于一常见的遵循泊松分布的中子源（如Am-Be中子源或252Cf中子源），若将其放置于一不含增殖介质的系统中，则系统内中子探测器计数分布将遵循泊松分布，即中子探测器计数的方差与平均值相同，其方差-平均值比为1。若中子源放置在含有铀和钚等增殖介质的系统中，则中子将引发链式裂变反应，由1个中子引发的裂变可能产生多于1个的中子，这将导致系统内的中子之间产生相关性，中子的产生和被探测过程不再是独立事件，其概率分布也将偏离泊松分布，从而使中子探测器计数的方差-平均值比大于1。这个大于1的部分可用Feynman-Y 方程Y（t）表示：

式中：Z（t）为时间窗长度为t时的中子探测器计数；〈Z（t）〉为探测器计数的一阶矩，即探测器计数在探测时间窗长度为t时的平均值；σ（t）2为探测器计数的方差。Y（t）也被称作Feynman-Y 方程，它描述了中子计数的方差-平均值比值相对于1的偏移量，反映了随机变量的分布相对于泊松分布的偏移程度。

1.2 中子探测器计数方差和平均值的求解方法

中子产生和被探测属于随机过程，因此可运用统计物理学的方法对系统内粒子数量随时间变化的关系进行研究，求解中子探测器计数的方差和均值，从而得到Feynman-Y 方程。对于随机过程，利用构造生成函数的方法可求解随机变量的方差和均值［6］。生成函数是一类以概率密度函数为系数的幂级数，若随机变量N（t）的概率密度函数为P（N，t），则可定义其生成函数为：

对生成函数求各阶导数，可求得随机变量的各阶阶乘矩，进而求得随机变量的期望和方差。例如对于式（2），若先对X 求导，再令X＝1，即可求得随机变量N（t）一阶阶乘矩，即N（t）的期望（用尖括号表示）：

若在式（2）中对X 求二阶导数，再令X＝1，则可求得随机变量N（t）二阶阶乘矩：

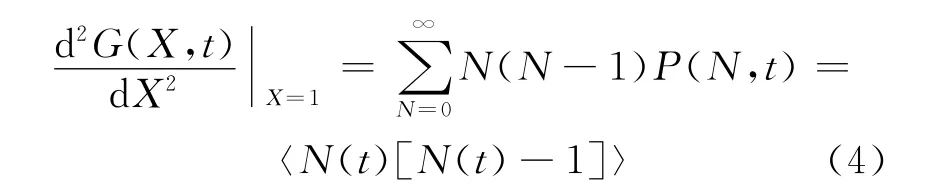
则随机变量的P（N，t）的方差可通过下式算出：

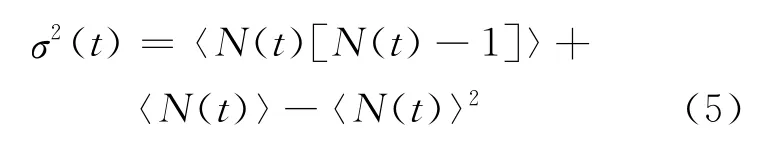
2 双区单群Feynman-α方程解析解推导

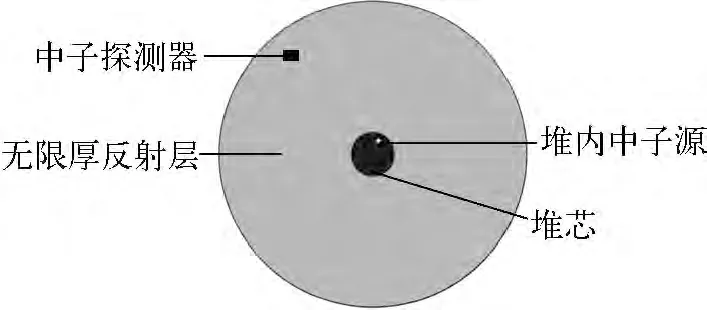
图1 双区次临界系统模型示意图Fig.1 Schematic diagram of two-region subcritical system

构造1个由堆芯和无限厚反射层构成的双区次临界系统模型（图1），1个遵循泊松分布的中子源位于堆芯内部，源强为S，中子探测器位于反射层内。用P（NA，NB，C，Z，t）表示系统在t时刻处于某种状态的概率，即在这种状态下，系统中堆芯区域中子数为NA、反射层区域中子数为NB、堆内缓发中子先驱核数为C 且在0到t时间段内探测器中子计数为Z。

假设在单位时间内，反应堆内1个粒子（可能为中子或缓发中子先驱核）发生某种反应X的概率（即反应强度）为λX。若系统中已经存在的粒子数为n，则在dt时间内，粒子发生某种反应X 的概率为：

堆芯区域（区域A）中子可能发生的反应包括：中子被堆内燃料和材料吸收、中子迁移到反射层（区域B）、中子被核燃料吸收并引发裂变反应。反射层区域（区域B）中子可能发生的反应有：中子被反射层内材料吸收、中子迁移到堆芯区域（区域A）、中子被探测器探测。单位时间内1个粒子发生各类反应的反应强度用不同字母表示（表1）。

表1 系统内粒子可能发生的反应类型和反应强度Table 1 Possible reaction types and reaction intensities for different particles in system

在dt时间内，除表1所列的反应类型外，系统内的中子和缓发中子先驱核还可能均不发生任何反应，发生这种情况的概率可写为：

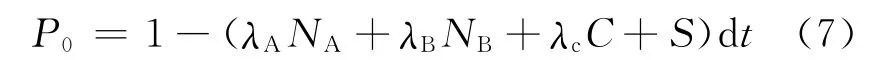
则在t到dt时间内，系统状态的变化可表示为：

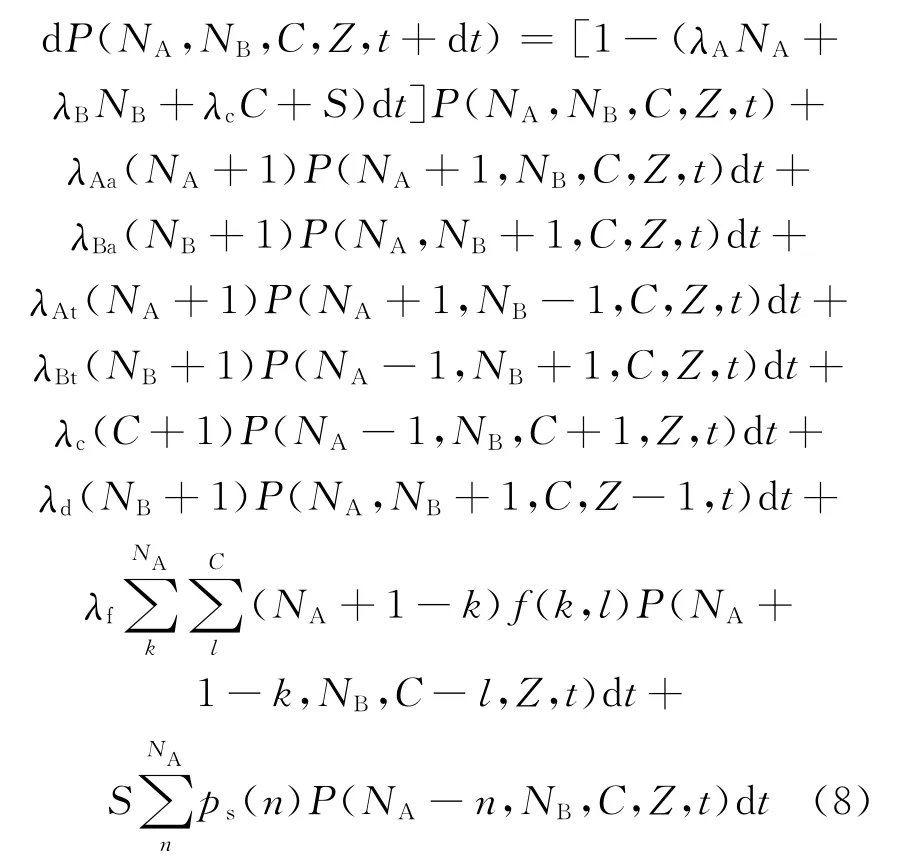
将式（8）写成微分形式，则可构成一描述系统变化情况的前向主方程：

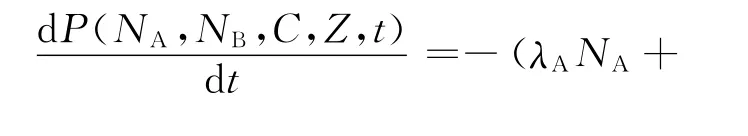
其中：f（k，l）为裂变产生中子数量（k）和缓发中子先驱核数量（l）的概率密度函数；ps（n）为中子源每次释放中子数量（n）的概率密度函数。

2.1 求解中子探测器计数期望值表达式

对概率密度函数P（NA，NB，C，Z，t）定义生成函数，有：

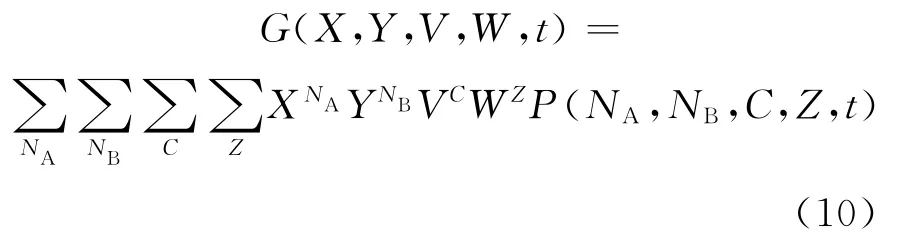
由于函数P（NA，NB，C，Z，t）的微分形式相对于其本身更易求得，因此将式（10）写成微分形式，有：

将式（9）代入式（11）并经过化简，可得：

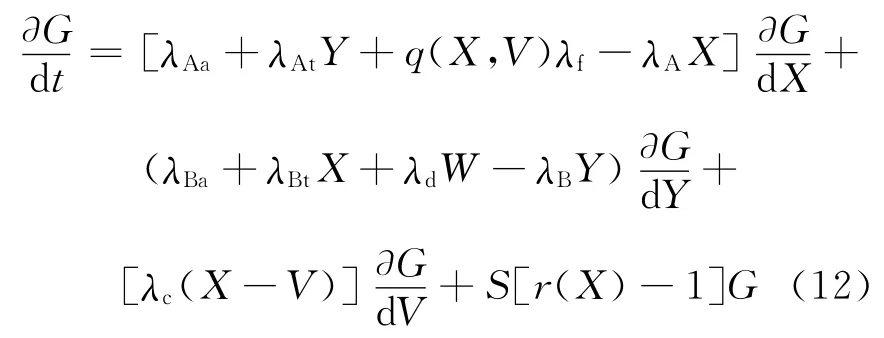
为简化书写，将式（11）中G（X，Y，V，W，t）简写为G。在式（12）中，q（X，V）为概率密度函数f（k，l）的生成函数，定义为：

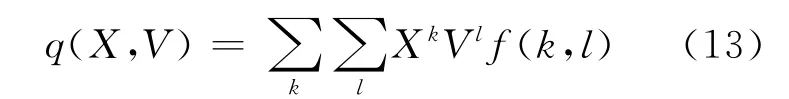
r（X）为概率密度函数ps（n）的生成函数，定义为：

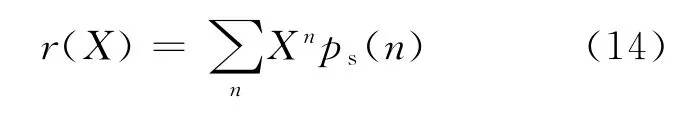
通过生成函数，可计算出探测器计数的一阶阶乘矩和二阶阶乘矩。分别对式（12）中的X、Y、V、W 求导，并令参数X＝Y＝V＝W ＝1，可得系统内粒子数量的一阶阶乘矩的导数。一阶阶乘矩的导数描述了系统内各种粒子数的平均值随时间变化的情况，其中式（15）中的3个微分方程分别描述了系统内堆芯区域中子数NA、反射层区域中子数NB、以及缓发中子先驱核数C 的平均值随时间变化的情况。式（16）则描述了中子探测器计数Z 的期望值随时间变化的情况：

其中：

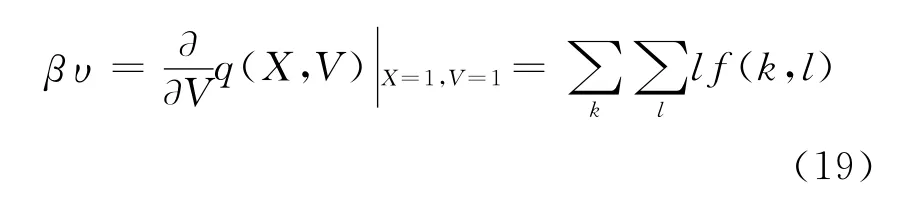
在一源强度不变的次临界系统中，当时间足够长时，系统内中子的消耗速率与中子源强度相同，系统达到稳态，系统内各类粒子数的平均值不再随时间变化，因此各类粒子数的平均值对时间的导数为零，即式（15）中3个微分方程左边均为0，则式（15）化为了1 个以系统稳态条件下堆芯部分中子数期望值NA、反射层内中子数期望值NB、堆芯内缓发中子先驱核数期望值C 为变量的三元一次方程组，解此方程组可得：

而通过式（16）可看出，探测器中子计数Z与时间t呈线性关系。对式（16）的时间变量t积分可得中子探测器计数期望值〈Z（t）〉随探测时间长度变化的表达式：

2.2 求解中子探测器计数方差的表达式

通过生成函数无法直接求解中子探测器计数的方差。但可通过间接方法定义修正二阶矩μ 来计算［5］。将修正二阶矩μ 定义为：

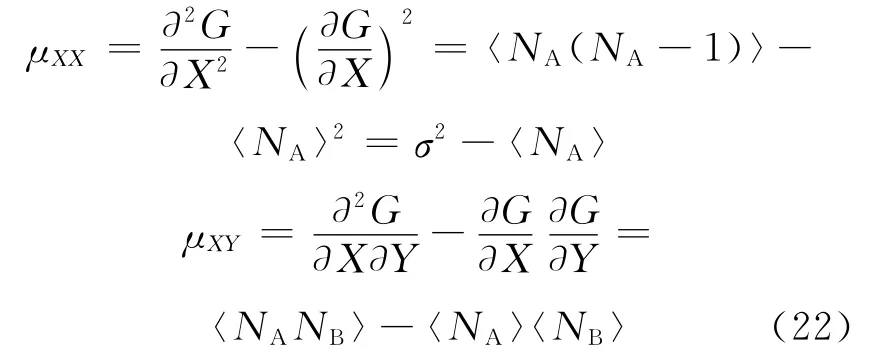
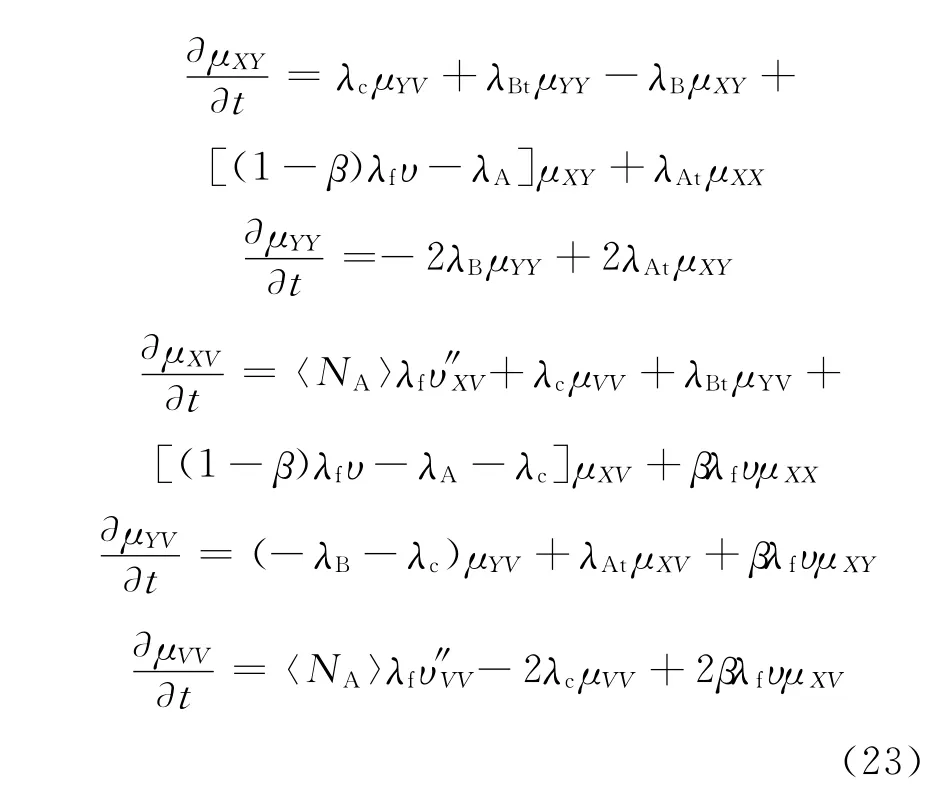
其中：

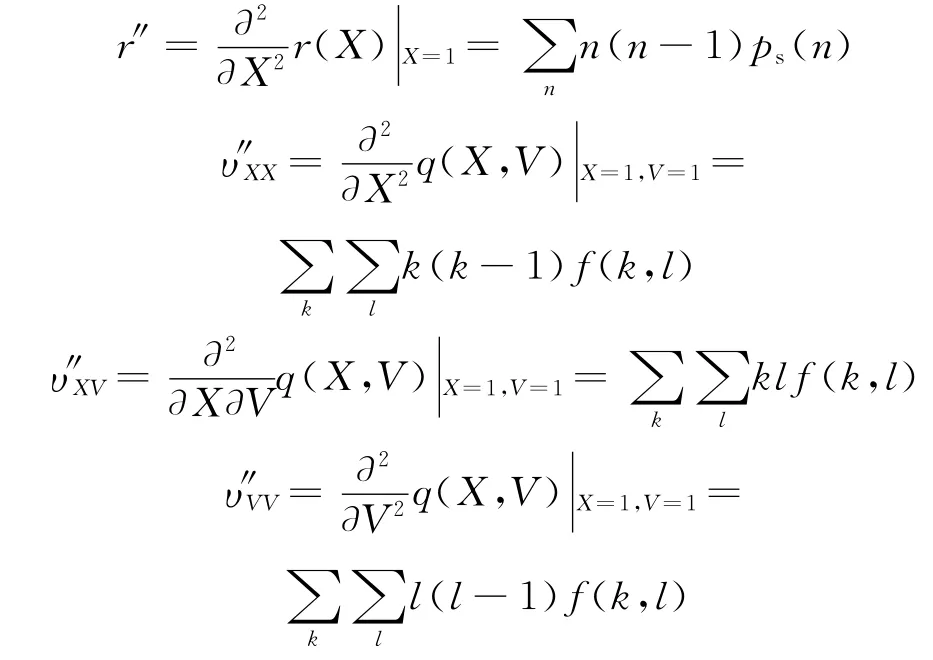
当探测时间足够长，系统处于稳态，与探测器计数无关的各修正二阶矩为定值，不随时间变化，其导数也为零。因此式（23）中6个方程的左边均为0，则方程组化为以各修正二阶矩为变量的六元一次方程组，解此方程可解得与探测器计数无关的各修正二阶矩μXX、μXY、μYY、μXV、μYV、μVV。此 六 元 一 次 方 程 组 可 通 过Mathematica等数学软件求解，但最终得到的解篇幅较长，因此这里未写出解的具体表达式。

而与探测器计数有关的修正二阶矩μXW、μYW、μVW、μWW 对时间的导数也可通过式（22）给出的计算方法得到：

当系统处于稳态时，探测器计数仍随时间变化而增加，与探测器有关的修正二阶矩不为定值，因此式（24）不能转化为普通方程组求解。为求解式（24），可将其中的3个方程看作是以μXW、μYW、μVW 为变量的微分方程组，利用拉普拉斯变换将之转化为线性方程组求解。通过这种方法可解得μXW（t）、μYW（t）、μVW（t）的拉普拉斯变换。其中μYW（t）的拉普拉斯变换为：

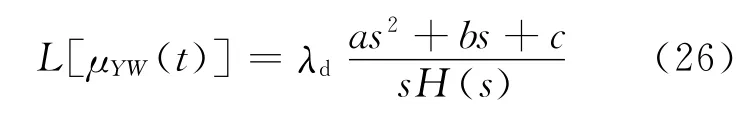
其中：

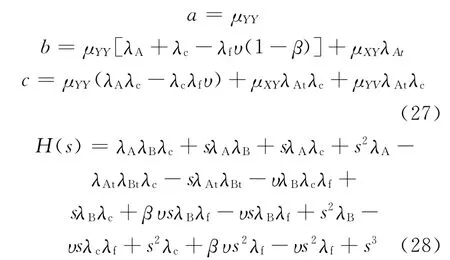
H（s）是关于s的三次方程，求解可得到其3个实根，设这3个根分别为-ω1、-ω2、-ω3，即：

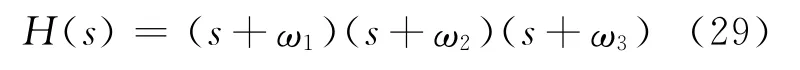
对式（26）进行拉普拉斯逆变换，可得μYW（t）：

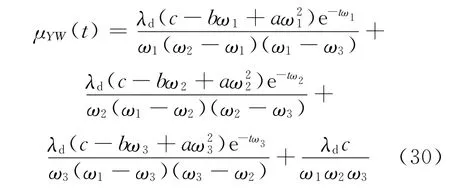
将式（30）代入式（25），并对t在0到t区间积分，得：

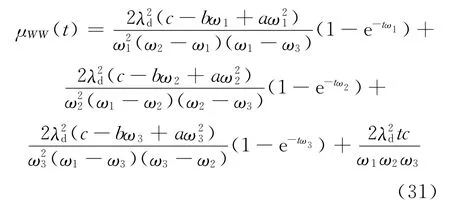
根据式（1）和式（22）中第1个等式，Feynman-Y 方程可用探测器中子计数的平均值〈Z（t）〉和修正二阶矩μWW（t）表示：

因此，将式（21）和式（31）做比值并化简，即得到双区单群Feynman-α方程的解析解：

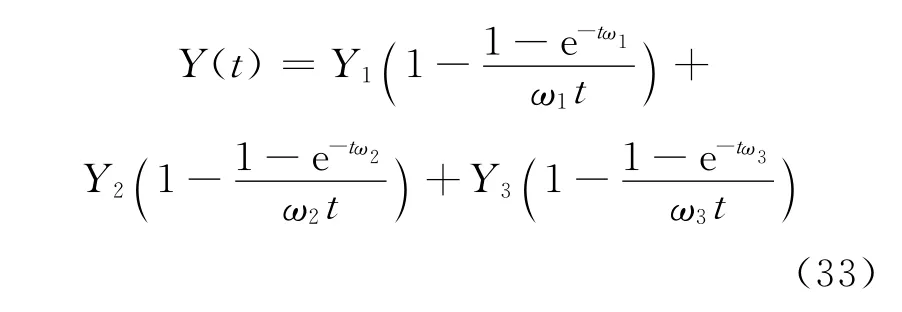
其中：

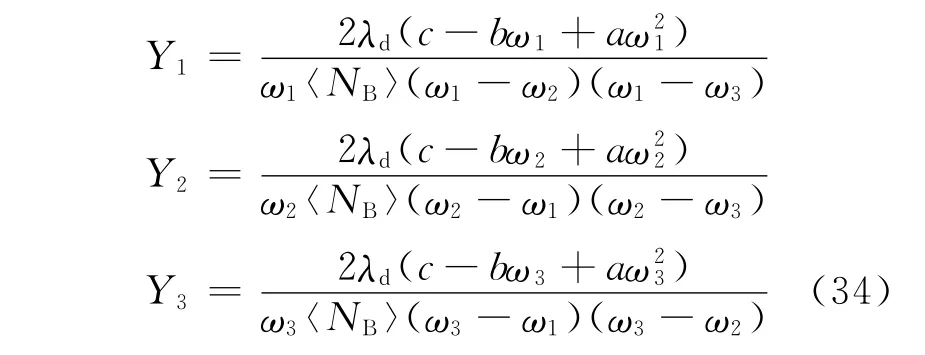
3 总结

利用统计物理学方法，通过构造前向主方程，描述了一双区次临界系统的状态变化情况，并利用生成函数的性质，求解了系统内中子探测器计数的方差σ2（t）和平均值〈Z（t）〉，进而求得双区单群Feynman-α方程的解析解，得到了中子探测器计数的方差-平均值比值随探测器计数时间变化的关系。目前已有的工作仅限于对双区单群Feynman-α 方程的解析解的推导。在下一步的工作中，将尝试利用蒙特卡罗程序建立计算模型，验证双区Feynman-α方程用于次临界度求解的有效性，并与单区单群Feynman-α方法的计算结果进行对比。

［1］ FEYNMAN R P，de HOFFMANN F，SERBER R.Dispersion of the neutron emission in U-235 fission［J］.Journal of Nuclear Energy，1956，3（1）：64-IN10.

［2］ PÁZSIT I，KITAMURA Y，WRIGHT J，et al.Calculation of the pulsed Feynman-alpha formulae and their experimental verification［J］.Annals of Nuclear Energy，2005，32（9）：986-1 007.

［3］ TESINSKY M，BERGLÖF C，BÄCK T，et al.Comparison of calculated and measured reaction rates obtained through foil activation in the subcritical dual spectrum facility YALINA-Booster［J］.Annals of Nuclear Energy，2011，38（6）：1 412-1 417.

［4］ CHERNIKOVA D，PÁZSIT I，ZIGUAN W.Application of the two-group-one-region and tworegion-one-group Feynman-alpha formulas in safeguards and accelerator-driven system （ADS）［C］∥Proceeding of ESARDA Meeting 2013.［S.l.］：［s.n.］，2013.

［5］ CHERNIKOVA D，ZIGUAN W，PÁZSIT I，et al.A general analytical solution for the varianceto-mean Feynman-alpha formulas for a two-group two-point，a two-group one-point and a onegroup two-point cases［J］.The European Physical Journal Plus，2014，129（11）：1-27.

［6］ PÁZSIT I，PÁL L.Neutron fluctuations：A treatise on the physics of branching processes［M］.The Netherlands：Elsevier，2007：231-239.