差分化节点特征对复杂网络链接预测的分类性能分析＊

伍杰华，朱岸青，蔡雪莲，张小兰

（1.广东工贸职业技术学院计算机工程系，广东 广州510510；2.华南理工大学信息科学与技术学院，广东 广州510641；3.暨南大学信息科学与技术学院，广东 广州510632）

1 引言

复杂网络分析［1］是数据挖掘和机器学习领域其中一个非常活跃的研究方向，其主要通过学习网络中实体及其相互之间的活动关系，发掘其中内在的知识。而该类关系和活动可以用网络或者图的结构［2］来表示，其中节点（顶点）表示一个实体，链接（边）表示两个实体之间的关系，利用网络图我们可以挖掘其结构特征并找出感兴趣的信息，社区发现、信息传播、节点分类等都是复杂网络分析研究的方向，本文主要针对链接预测这一领域开展研究。

链接预测根据网络的历史结构信息预测其演化方式及链接关系发生的潜在可能，其在众多领域有着重要的应用价值。例如，通过分析生物信息网络，预测氨基酸内蛋白质的相互作用；在社交网络中预测现在尚未成为朋友的未来是否“应该是朋友”［3］；在市场营销网络中判断哪些客户应该需要去开发等等。

2 相关工作

链接预测作为数据挖掘和复杂网络分析的研究方向已经有一些工作正在开展，主要分为基于网络结构信息挖掘的链接预测［4］和基于机器学习的链接预测两类［5］：（1）基于结构信息挖掘预测模型。其主要通过计算节点间的相似度获得，相似度表示两个节点之间（后称节点对）结构属性的相似性及产生链接可能性，假设相似性越大，它们之间存在链接的可能性就越大。Liben－Nowell D 和Kleinberg J［4］总结了基于网络拓扑结构的相似性定义方法，将这些指标分为基于节点和基于路径的两类，并分析了若干指标对的相互作用，及其对网络链接预测的效果。后续的许多工作都是在此基础上开展的［6，7］。（2）基于机器学习理论的链接预测模型。给定一个网络数据集，其训练集的先验类别（存在链接或者不存在）易知，所以该类模型的算法基本都是通过有监督学习－分类的思想开展，其主要分为以下几类：关系图模型［8］主要用可视化的方式（即图的形式）表示较为抽象的随机变量依赖关系，把链接产生可能性定义为概率，并通过图的潜在知识进行估计；基于贝叶斯的链接预测把产生链接的可能看成是给定特征和参数前提下的条件概率，并把该条件概率转变为非参数化学习［9］、最大间隔分类等问题［10］和迁移学习模型［11］等。

本文研究两类预测方向结合中所遇到的问题——分类模型所获取的特征不能完全反映复杂网络的拓扑属性。图1是一个网络图模型，黑点代表节点，实线代表链接，虚线代表预测链接，点线代表共邻节点之间的链接。从图1可以看到，AB是预测链接，C、D、E是三个共邻节点特征，对于图1两子图中共邻节点对的联系，显然子图b比子图a要紧密，所以其共邻节点的属性不一样，那么其对AB预测的影响显然也不一样。所以，尽管两图共邻节点数目的特征值均为3，但是由于其共邻节点属性不同，那么根据网络聚集原理，子图b中AB产生链接的可能性更大。因此，如何提取该类特征对分类学习显示尤其重要。

Figure 1 Network model based on neighbors topology feature图1 基于节点拓扑特征的网络模型

本文首先定义复杂网络的具备不同特征的拓扑结构特征属性，然后提出赋予具备不同属性共同邻接节点的贡献权重的特征，结合不同分类模型下链接预测算法思想，通过对八个真实网络进行实验比较其性能，同时分析不同特征对于预测结果的影响。

综合来说，本文的贡献主要有以下三点：

（1）引入基于朴素贝叶斯算法LNB（Local Naive Bayesian）［12］共邻节点的贡献作为特征并给出基于节点、共邻节点结构属性定义。

（2）解释差异化的网络拓扑结构特征对分类性能的影响。

（3）分析不同的有监督－分类模型下链接预测的性能，给定不同噪音对预测性能的影响。

3 问题定义

3.1 网络定义

G＝（V，E，R）定义为复杂网络的无向图模型，V和E⊆V×V分别为模型中节点和链接的集合，R定义为网络中的关系，节点u，v∈V形成的链接e∈E被认为是R上定义的一个关系，其映射函数为：：V×V×R→E。其中（u，v）为节点对，Γ（u，v）＝Γ（u）∩Γ（v）为节点对的共邻节点集合。

3.2 问题描述

有监督学习是经典的机器学习思想，它利用一组已知类别的样本调整分类器的参数，使其达到所要求分类性能的过程。给定一个网络G，随机移除20%的边，剩下的作为训练集，记为GT，移除的边作为预测集，记为GP，为了更好地获取其分类性能，我们分别对GT和GP加上一组不属于G且随机生成的噪声GN。分类模型的目的在于对训练集GT的学习获取分类模型，并应用到预测集GP中进行链接预测。

3.3 数据集

为了评价算法的有效性，本文采用具备不同拓扑属性的八个真实网络进行实验，该网络涵盖了社会、生物、电话、交通等各个领域的数据，其度分布均满足Babárasi A L［13］提出的无尺度网络分布—幂律分布，具体如图2所示，同时各网络的结构属性参照表1。

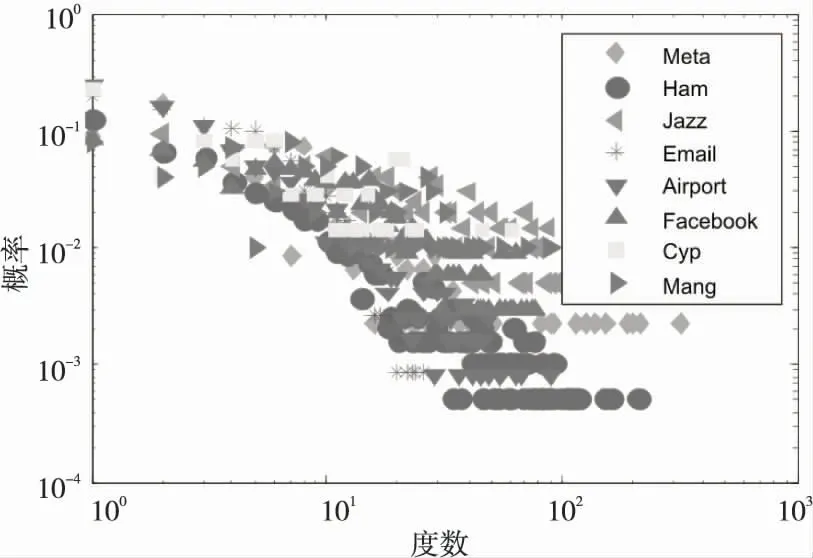
Figure 2 Degree distribution of true networks图2 真实网络的度分布

Table 1 Attributes of network structure表1 网络结构属性表

表1中｜V｜和｜E｜是网络的节点和链接数目，c＊、d＊和p＊分表代表聚类系数、平均度和平均路径。

4 特征获取和分类模型

4.1 基本拓扑结构特征获取

特征是进行分类学习的必要条件，结合本文定义，给定一个预测节点对，主要通过计算两节点的属性及其相似度属性［4，12］获取相关特征，该类特征分为节点和共邻节点特征等几类。

4.1.1 基于节点属性的特征

（1）PA（Preferential Attachment）：PA 是 链接，趋向于出现在度比较高的节点对之间，其定义：

（2）CC（Clustering Coefficient）：CC是表示一个图形中节点聚集程度的系数，由于相对高密度连接点的关系，链接总是趋向于出现在以下这样一组严密的组织关系中［14］，定义为：

（3）PR（Page Rank）：PR 是Google用于标识网页的等级/重要性的一种方法，也适用于对复杂网络节点进行排序，链接也是倾向于出现在排序较高的节点对之间，其公式和算法相对复杂，具体可参考［4］。

（4）Katz（Path Count）：计算两个节点之间存在的路径数目，定义为：

（5）APD（Average Path Distance）：计算两个节点之间的平均路径长度：

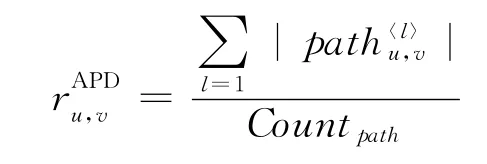
4.1.2 基于共邻节点的特征

该经典特征通过计算两节点共同邻居ω的属性获得，本文主要通过其拓扑结构信息获取相关特征：

（1）CN（Common Neighbors）：共邻节点的数目：

（2）AA（Adamic－Adar）：共邻节点度的对数分子和：

（3）RA （Resource Allocation）：共邻节点度的分子和：

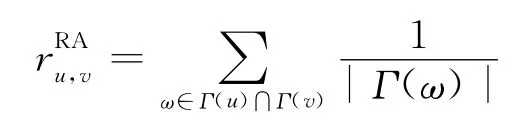
4.2 基于差分化节点贡献的特征获取

基于共邻节点的相似度算法假设所有节点对预测节点对的贡献权重视为一致，不利于区分具备不同属性共邻节点的角色及其贡献。Liu Z 等人［12］提出可以把预测链接看成两类分类模型，e和分别视为链接存在和不存在，并把其存在的概率定义为给定一组共邻节点的条件概率P（e｜Γ（u，v））：

由于Γ（u，v）是共邻节点的集合，直接计算较为困难，所以在此假设各个共邻节点对预测链接的影响是独立的，那么基于朴素贝叶斯的独立性理论，式（1）可以转变为以下两个公式：

在式（2）中，每一个共邻节点对链接产生的影响由P（ωi｜e）或者给出，为了简化运算，我们定义式（2）和式（3）的比率为共邻节点的关系：

式（4）的左部分是网络中链接的比率，右部分则为节点的贡献：

Rω定义为节点的贡献权重，其中e是（x，y）存在链接，为该节点的聚类系数，从而经典的CN 算 法 改 进 后 定 义 为LNB－CN（Local Naive Bayesian Common Neighbors）：

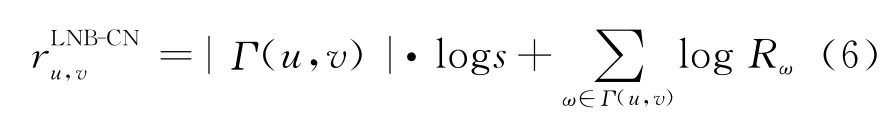
同理，AA 和RA 形式的LNB特征如下所示：

LNB－AA（Local Naive Bayesian Common Adamic－Adar）：

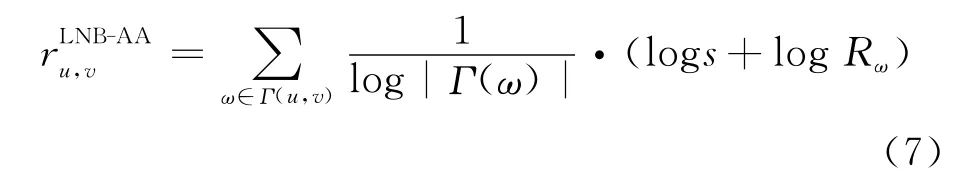
LNB－RA（Local Naive Bayesian Resource Allocation）：

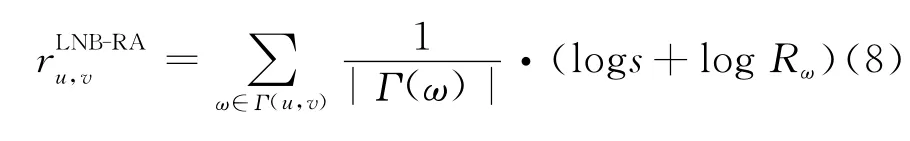
4.3 分类模型

有监督学习是分类机器学习和数据挖掘领域最基本的模型，下面是本文使用的部分经典算法模型：（1）线性判别分析LDA （Linear Discriminate Analysis）；（2）二次判别分析QDA（Quadratic Discriminate Analysis）；（3）朴素贝叶斯NB（Naïve Bayesian）；（4）分类树CT（Classification Tree）；（5）退化树RT（Regression Tree）；（6）K 近邻分类KNN（K－Nearest Neighbor）；（7）支持向量机SVM（Support Vector Machine）。

5 实验评价

5.1 实验评价模型

本实验基于Complex Networks Package for MatLab［15］平 台 和Matlab 自 带 的Machine learning包。预测精确度采用10－folder交叉验证方法进行，交叉重复验证10次，每次随机产生一个训练集GT和一个预测集GP作为测试集，并将10次的平均交叉验证precision作为评价指标。precision指的是训练集中分类正确的数目和目标集应分类数目的比率。

实验首先比较各种特征的分类精确度，然后整合三类特征，比较各类有监督分类模型的性能。

5.2 实验结果与分析

5.2.1 分类准确度

从表2和图3中的实验结果可以看出，判别分析（LDA，QDA）和KNN 的结果相对其他模型要好，其中LDA 为最优分类器，其平均预测精确度达到0.819 6（见图3a），同时，从图3b 看出，Jazz数据集的分类准确度是最高的，达到0.899 8，这是由于该网络的拓扑结构特征密度较高，其聚类系数和平均度分别达到0.64 和27.69，造成特征差异化明显，从而提高了分类精确度；同时，该特性也使Facebook数据集的分类效果最差。

此外，我们在预测集GP加上一组不属于G且与其集合长度有关并随机生成的噪声GN，实验中分别取GP概率0.1～0.9的九组噪声进行预测，实验结果参考图3c。从图3曲线的方向我们可以看出，分类精确度随着噪声数据集比率的增多而递增，这是由于噪声数据是随机生成的一组不存在的链接集合，这些不存在（类别的0）的链接具备差异化较为明显的特征，有助于分类模型更好地学习和划分。

5.2.2 特征集选择

复杂网络的特征是分类的基础，特征选择的好坏对于分类的精度会产生重要的影响，本文分别针对基于节点信息、共邻节点信息和链接路径信息三类特征给出实验结果。从图4a～图4c可以看出，基于共邻节点的特征分类精度最佳，达到0.76，其他两类特征的精度则在0.7左右，这一结果也符合目前链接预测的研究方向，因为基于共邻节点相似度的方法一直都是既简单又有效的预测算法；同时也表明，本文引入的共邻节点的角色及其贡献作为特征的有效性。

Table 2 Comparison of link prediction precision of different classifiers表2 不同分类模型对链接预测精确度

Figure 3 Different feature prediction precision and relation functions图3 特征预测精度及关系函数

Figure 4 Comparison of prediction precision of different classifiers图4 不同分类器的分类精度比较

5.2.3 案例简介

图5a 和图5b 给出了各分类器对Metabolic——生物网络的分类效果的ROC 曲线，图5c则展示了最优分类器LDA 对最有效的LNB－AA、LNB－RA 属性分类器的效果。

Figure 5 Comparison of different classifiers Metabolic networks图5 各分类器对Metabolic网络的预测分类

6 结束语

本文研究了基于复杂网络拓扑结构特征的有监督学习－分类模型的问题。主要引入了朴素贝叶斯模型定义的共邻节点贡献作为网络的拓扑结构特征进行学习和分类，同时探讨了有监督学习模型对链接预测性能的影响。八个真实网络的实验表明，提出的LNB特征有较优的分类预测性能，同时发现差异化的特征选择在不同的分类模型下预测效果存在一定的规律。但是，本文的实验数据网络都是同构的，分析分类模型对异构和多维网络的预测性能是下一步需要开展的工作。

［1］ Samuel L.Social networks：A developing paradigm［M］.New York：Academic Press，1977.

［2］ Wasserman S，Faust K.Social network analysis：Methods and applications［M］.Cambridge：Cambridge University Press，1994.

［3］ Leskovec J，Huttenlocher D，Kleinberg J.Predicting positive and negative links in online social networks［C］∥Proc of the 19th International Conference on World Wide Web，2010：641－650.

［4］ Liben－Nowell D，Kleinberg J.The link prediction problem for social networks［J］.Journal of the American Society for Information Science and Technology，2007，58（7）：1019－1031.

［5］ Al Hasan M，Chaoji V，Salem S，et al.Link prediction using supervised learning［C］∥Proc of Workshop on Link Analysis，Counterterrorism and Security，2006：1.

［6］ Donghyuk S，Si Si，Dhillon I S.Multi－scale link prediction［EB/OL］.［2012－04－08］.http：arxiv.org/abs/1206.1891.

［7］ Valverde－Rebaza J C，de Andrade Lopes A.Link prediction in complex networks－based on cluster information［C］∥Proc of SBIA’12，2012：92－101.

［8］ Popescul A，Ungar L H.Statistical relational learning for link prediction［C］∥Proc of IJCAI Workshop on Learning Statistical Models from Relational Data，2003：1.

［9］ Miller K，Griffiths T，Jordan M.Nonparametric latent feature models for link prediction［C］∥Proc of Advances in Neural Information Processing Systems，2009：1276－1284.

［10］ Zhu J.Max－margin nonparametric latent feature models for link prediction［EB/OL］.［2012－12－10］.http：arxiv.rog/abs/1206.4659.

［11］ Cao B，Liu N N，Yang Q.Transfer learning for collective link prediction in multiple heterogenous domains［C］∥Proc of the 27th International Conference on Machine Learning，2010：159－166.

［12］ Liu Z，Zhang Q M，LüL，et al.Link prediction in complex networks：A local naïve Bayes model［J］.EPL（Europhysics Letters），2011，96（4）：48007.

［13］ Barabási A L，Réka A.Emergence of scaling in random networks［J］.Science，1999，286：509－512.

［14］ Feng X，Zhao J C，Xu K.Link prediction in complex networks：A clustering perspective［J］.The European Physical Journal B，2012，85（1）：1－9.

［15］ http：//www.levmuchnik.